Varyans

Aynı ortalamaya ancak farklı varyanslara sahip iki popülasyondan alınan örneklemler. Kırmızı popülasyonun ortalaması 100 ve varyansı 100 (SD=10) iken mavi popülasyonun ortalaması 100 ve varyansı 2500'dür (SD=50). ⓘ

Olasılık teorisi ve istatistikte varyans, rastgele bir değişkenin popülasyon ortalamasından veya örnek ortalamasından karesel sapma beklentisidir. Varyans bir dağılım ölçüsüdür, yani bir dizi sayının ortalama değerlerinden ne kadar uzağa yayıldığının bir ölçüsüdür. Varyans istatistikte merkezi bir role sahiptir; varyansın kullanıldığı bazı fikirler arasında tanımlayıcı istatistikler, istatistiksel çıkarım, hipotez testi, uyum iyiliği ve Monte Carlo örneklemesi yer alır. Varyans, verilerin istatistiksel analizinin yaygın olduğu bilimlerde önemli bir araçtır. Varyans, standart sapmanın karesi, bir dağılımın ikinci merkezi momenti ve rastgele değişkenin kendisiyle olan kovaryansıdır ve genellikle şu şekilde gösterilir $\sigma ^{2}$, $s^{2}$, $\operatorname {Var} (X)$, $V(X)$veya $\mathbb {V} (X)$. ⓘ

Bir dağılım ölçüsü olarak varyansın bir avantajı, beklenen mutlak sapma gibi diğer dağılım ölçülerine kıyasla cebirsel manipülasyona daha uygun olmasıdır; örneğin, ilişkisiz rastgele değişkenlerin toplamının varyansı, varyanslarının toplamına eşittir. Pratik uygulamalar için varyansın bir dezavantajı, standart sapmanın aksine, birimlerinin rastgele değişkenden farklı olmasıdır, bu nedenle hesaplama bittikten sonra standart sapma daha yaygın olarak bir dağılım ölçüsü olarak rapor edilir. ⓘ

Her ikisi de "varyans" olarak adlandırılan iki farklı kavram vardır. Biri, yukarıda tartışıldığı gibi, teorik bir olasılık dağılımının parçasıdır ve bir denklemle tanımlanır. Diğer varyans ise bir dizi gözlemin bir özelliğidir. Varyans gözlemlerden hesaplandığında, bu gözlemler tipik olarak gerçek bir dünya sisteminden ölçülür. Sistemin tüm olası gözlemleri mevcutsa, hesaplanan varyansa popülasyon varyansı denir. Ancak normalde sadece bir alt küme mevcuttur ve bundan hesaplanan varyansa örneklem varyansı denir. Bir örneklemden hesaplanan varyans, tüm popülasyon varyansının bir tahmini olarak kabul edilir. Aşağıdaki bölümde tartışıldığı gibi, popülasyon varyansının bir tahminini hesaplamanın birden fazla yolu vardır. ⓘ

Bu iki varyans türü birbiriyle yakından ilişkilidir. Nasıl olduğunu görmek için, teorik bir olasılık dağılımının varsayımsal gözlemlerin bir üreticisi olarak kullanılabileceğini düşünün. Bir dağılım kullanılarak sonsuz sayıda gözlem üretilirse, bu sonsuz kümeden hesaplanan örneklem varyansı, dağılımın varyans denklemi kullanılarak hesaplanan değerle eşleşecektir. ⓘ

Bir reel sayı halinde olan rassal değişkenin varyansı o rassal değişkenin ikinci merkezsel momenti ve aynı zamanda ikinci kümülantı olur. Eğer varyans değeri var ise, ortalama değeri de vardır. Ama bunun aksi doğru değildir. ⓘ

Tanım

Rastgele bir değişkenin varyansı $X$ 'nin ortalamasından karesel sapmanın beklenen değeridir. $X$, $\mu =\operatorname {E} [X]$:

$\operatorname {Var} (X)=\operatorname {E} \left[(X-\mu )^{2}\right].$

Bu tanım, kesikli, sürekli, her ikisi de olmayan veya karışık süreçler tarafından üretilen rastgele değişkenleri kapsar. Varyans, rastgele bir değişkenin kendisiyle olan kovaryansı olarak da düşünülebilir:

$\operatorname {Var} (X)=\operatorname {Cov} (X,X).$

Varyans aynı zamanda bir olasılık dağılımının ikinci kümülantına eşdeğerdir. $X$. Varyans tipik olarak şu şekilde belirlenir $\operatorname {Var} (X)$ya da bazen $V(X)$ veya $\mathbb {V} (X)$veya sembolik olarak $\sigma _{X}^{2}$ ya da basitçe $\sigma ^{2}$ ("sigma kare" olarak telaffuz edilir). Varyans ifadesi aşağıdaki şekilde genişletilebilir:

${\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\[4pt]&=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}\end{aligned}}$ ⓘ

Başka bir deyişle, X'in varyansı X'in karesinin ortalamasından X'in ortalamasının karesinin çıkarılmasına eşittir. Bu denklem kayan noktalı aritmetik kullanan hesaplamalar için kullanılmamalıdır, çünkü denklemin iki bileşeni büyüklük olarak birbirine benziyorsa feci iptallerden muzdariptir. Sayısal olarak kararlı diğer alternatifler için varyans hesaplama algoritmaları bölümüne bakınız. ⓘ

Ayrık rastgele değişken

Eğer rastgele değişken üreteci $X$ olasılık kütle fonksiyonu ile ayrıktır $x_{1}\mapsto p_{1},x_{2}\mapsto p_{2},\ldots ,x_{n}\mapsto p_{n}$, sonra ⓘ

$\operatorname {Var} (X)=\sum _{i=1}^{n}p_{i}\cdot (x_{i}-\mu )^{2},$ ⓘ

nerede $\mu$ beklenen değerdir. Yani, ⓘ

$\mu =\sum _{i=1}^{n}p_{i}x_{i}.$ ⓘ

(Böyle bir ayrık ağırlıklı varyans, toplamı 1 olmayan ağırlıklarla belirtildiğinde, ağırlıkların toplamına bölünür). ⓘ

Bir koleksiyonun varyansı $n$ eşit olasılıklı değerler şu şekilde yazılabilir ⓘ

$\operatorname {Var} (X)={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}$ ⓘ

nerede $\mu$ ortalama değerdir. Yani, ⓘ

$\mu ={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.$ ⓘ

Bir kümenin varyansı $n$ Eşit olasılıklı değerler, doğrudan ortalamaya atıfta bulunmaksızın, noktaların birbirlerine olan tüm çift yönlü karesel uzaklıklarının karesel sapmaları cinsinden eşdeğer olarak ifade edilebilir:

$\operatorname {Var} (X)={\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}{\frac {1}{2}}(x_{i}-x_{j})^{2}={\frac {1}{n^{2}}}\sum _{i}\sum _{j>i}(x_{i}-x_{j})^{2}.$ ⓘ

Kesinlikle sürekli rastgele değişken

Eğer rastgele değişken $X$ bir olasılık yoğunluk fonksiyonuna sahiptir $f(x)$ve $F(x)$ karşılık gelen kümülatif dağılım fonksiyonu ise, o zaman ⓘ

${\begin{aligned}\operatorname {Var} (X)=\sigma ^{2}&=\int _{\mathbb {R} }(x-\mu )^{2}f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}f(x)\,dx-2\mu \int _{\mathbb {R} }xf(x)\,dx+\mu ^{2}\int _{\mathbb {R} }f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \int _{\mathbb {R} }x\,dF(x)+\mu ^{2}\int _{\mathbb {R} }\,dF(x)\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \cdot \mu +\mu ^{2}\cdot 1\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-\mu ^{2},\end{aligned}}$ ⓘ

ya da eşdeğer olarak, ⓘ

$\operatorname {Var} (X)=\int _{\mathbb {R} }x^{2}f(x)\,dx-\mu ^{2},$ ⓘ

nerede $\mu$ 'nin beklenen değeridir. $X$ tarafından verilen ⓘ

$\mu =\int _{\mathbb {R} }xf(x)\,dx=\int _{\mathbb {R} }x\,dF(x).$ ⓘ

Bu formüllerde, aşağıdakilere göre integraller $dx$ ve $dF(x)$ sırasıyla Lebesgue ve Lebesgue-Stieltjes integralleridir. ⓘ

Eğer fonksiyon $x^{2}f(x)$ her sonlu aralıkta Riemann ile bütünleştirilebilir $[a,b]\subset \mathbb {R} ,$ sonra ⓘ

$\operatorname {Var} (X)=\int _{-\infty }^{+\infty }x^{2}f(x)\,dx-\mu ^{2},$ ⓘ

burada integral bir uygun olmayan Riemann integralidir. ⓘ

Örnekler

Üstel dağılım

Parametresi λ olan üstel dağılım, olasılık yoğunluk fonksiyonu aşağıdaki şekilde verilen sürekli bir dağılımdır

$f(x)=\lambda e^{-\lambda x}$

aralığında [0, ∞). Ortalamasının şu şekilde olduğu gösterilebilir

$\operatorname {E} [X]=\int _{0}^{\infty }\lambda xe^{-\lambda x}\,dx={\frac {1}{\lambda }}.$ ⓘ

Parçalarla integral alarak ve daha önce hesaplanmış olan beklenen değeri kullanarak, şu sonuca ulaşırız:

${\begin{aligned}\operatorname {E} \left[X^{2}\right]&=\int _{0}^{\infty }\lambda x^{2}e^{-\lambda x}\,dx\\&=\left[-x^{2}e^{-\lambda x}\right]_{0}^{\infty }+\int _{0}^{\infty }2xe^{-\lambda x}\,dx\\&=0+{\frac {2}{\lambda }}\operatorname {E} [X]\\&={\frac {2}{\lambda ^{2}}}.\end{aligned}}$ ⓘ

Böylece, X'in varyansı şu şekilde verilir

$\operatorname {Var} (X)=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}={\frac {2}{\lambda ^{2}}}-\left({\frac {1}{\lambda }}\right)^{2}={\frac {1}{\lambda ^{2}}}.$ ⓘ

Adil zar

Altı yüzlü adil bir zar, her biri 1/6 eşit olasılığa sahip 1'den 6'ya kadar sonuçları olan ayrık bir rastgele değişken X olarak modellenebilir. X'in beklenen değeri $(1+2+3+4+5+6)/6=7/2.$ Bu nedenle, X'in varyansı

${\begin{aligned}\operatorname {Var} (X)&=\sum _{i=1}^{6}{\frac {1}{6}}\left(i-{\frac {7}{2}}\right)^{2}\\[5pt]&={\frac {1}{6}}\left((-5/2)^{2}+(-3/2)^{2}+(-1/2)^{2}+(1/2)^{2}+(3/2)^{2}+(5/2)^{2}\right)\\[5pt]&={\frac {35}{12}}\approx 2.92.\end{aligned}}$ ⓘ

N yüzlü bir zarın X sonucunun varyansı için genel formül şöyledir

${\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left(X^{2}\right)-(\operatorname {E} (X))^{2}\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}i^{2}-\left({\frac {1}{n}}\sum _{i=1}^{n}i\right)^{2}\\[5pt]&={\frac {(n+1)(2n+1)}{6}}-\left({\frac {n+1}{2}}\right)^{2}\\[4pt]&={\frac {n^{2}-1}{12}}.\end{aligned}}$ ⓘ

Yaygın olarak kullanılan olasılık dağılımları

Aşağıdaki tabloda yaygın olarak kullanılan bazı olasılık dağılımları için varyans listelenmektedir. ⓘ

Olasılık dağılımının adı	Olasılık dağılım fonksiyonu	Ortalama	Varyans ⓘ
Binom dağılımı	$\Pr \,(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}$	$np$	$np(1-p)$
Geometrik dağılım	$\Pr \,(X=k)=(1-p)^{k-1}p$	${\frac {1}{p}}$	${\frac {(1-p)}{p^{2}}}$
Normal dağılım	$f\left(x\mid \mu ,\sigma ^{2}\right)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$	$\mu$	$\sigma ^{2}$
Tekdüze dağılım (sürekli)	$f(x\mid a,b)={\begin{cases}{\frac {1}{b-a}}&{\text{for }}a\leq x\leq b,\\[3pt]0&{\text{for }}x<a{\text{ or }}x>b\end{cases}}$	${\frac {a+b}{2}}$	${\frac {(b-a)^{2}}{12}}$
Üstel dağılım	$f(x\mid \lambda )=\lambda e^{-\lambda x}$	${\frac {1}{\lambda }}$	${\frac {1}{\lambda ^{2}}}$
Poisson dağılımı	$f(k\mid \lambda )={\frac {e^{-\lambda }\lambda ^{k}}{k!}}$	$\lambda$	$\lambda$

Özellikler

Temel özellikler

Varyans negatif değildir çünkü kareler pozitif veya sıfırdır:

$\operatorname {Var} (X)\geq 0.$ ⓘ

Bir sabitin varyansı sıfırdır.

$\operatorname {Var} (a)=0.$ ⓘ

Tersine, bir rastgele değişkenin varyansı 0 ise, o zaman neredeyse kesinlikle bir sabittir. Yani, her zaman aynı değere sahiptir:

$\operatorname {Var} (X)=0\iff \exists a:P(X=a)=1.$ ⓘ

Varyans, bir konum parametresindeki değişikliklere göre değişmezdir. Yani, değişkenin tüm değerlerine bir sabit eklenirse, varyans değişmez:

$\operatorname {Var} (X+a)=\operatorname {Var} (X).$ ⓘ

Tüm değerler bir sabit ile ölçeklendirilirse, varyans bu sabitin karesi ile ölçeklendirilir:

$\operatorname {Var} (aX)=a^{2}\operatorname {Var} (X).$ ⓘ

İki rastgele değişkenin toplamının varyansı şu şekilde verilir

$\operatorname {Var} (aX+bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)+2ab\,\operatorname {Cov} (X,Y),$ ⓘ

$\operatorname {Var} (aX-bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)-2ab\,\operatorname {Cov} (X,Y),$ ⓘ

nerede $\operatorname {Cov} (X,Y)$ kovaryans değeridir. ⓘ

Doğrusal kombinasyonlar

Genel olarak, toplamı için $N$ rastgele değişkenler $\{X_{1},\dots ,X_{N}\}$varyans olur:

$\operatorname {Var} \left(\sum _{i=1}^{N}X_{i}\right)=\sum _{i,j=1}^{N}\operatorname {Cov} (X_{i},X_{j})=\sum _{i=1}^{N}\operatorname {Var} (X_{i})+\sum _{i\neq j}\operatorname {Cov} (X_{i},X_{j}),$

genel Bienaymé özdeşliğine de bakınız. ⓘ

Bu sonuçlar doğrusal bir kombinasyonun varyansını şu şekilde verir:

${\begin{aligned}\operatorname {Var} \left(\sum _{i=1}^{N}a_{i}X_{i}\right)&=\sum _{i,j=1}^{N}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})\\&=\sum _{i=1}^{N}a_{i}^{2}\operatorname {Var} (X_{i})+\sum _{i\not =j}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})\\&=\sum _{i=1}^{N}a_{i}^{2}\operatorname {Var} (X_{i})+2\sum _{1\leq i<j\leq N}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j}).\end{aligned}}$ ⓘ

Eğer rastgele değişkenler $X_{1},\dots ,X_{N}$ öyle ki

$\operatorname {Cov} (X_{i},X_{j})=0\ ,\ \forall \ (i\neq j),$

o zaman ilişkisiz oldukları söylenir. Daha önce verilen ifadeden, eğer rassal değişkenler $X_{1},\dots ,X_{N}$ ilişkisiz ise, toplamlarının varyansı varyanslarının toplamına eşittir veya sembolik olarak ifade edilir:

$\operatorname {Var} \left(\sum _{i=1}^{N}X_{i}\right)=\sum _{i=1}^{N}\operatorname {Var} (X_{i}).$ ⓘ

Bağımsız rastgele değişkenler her zaman ilişkisiz olduğundan (bkz. Kovaryans § İlişkisizlik ve bağımsızlık), yukarıdaki denklem özellikle rastgele değişkenler $X_{1},\dots ,X_{n}$ bağımsızdır. Dolayısıyla, bağımsızlık yeterlidir ancak toplamın varyansının varyansların toplamına eşit olması için gerekli değildir. ⓘ

Sonluluk sorunları

Cauchy dağılımında olduğu gibi, bir dağılım sonlu bir beklenen değere sahip değilse, varyans da sonlu olamaz. Ancak, bazı dağılımlar beklenen değerleri sonlu olmasına rağmen sonlu varyansa sahip olmayabilir. Buna bir örnek, indeksi sonlu olan bir Pareto dağılımıdır. $k$ tatmin eder $1<k\leq 2.$ ⓘ

İlişkisiz değişkenlerin toplamı (Bienaymé formülü)

Diğer dağılım ölçüleri yerine varyansın kullanılmasının bir nedeni, ilişkisiz rastgele değişkenlerin toplamının (veya farkının) varyansının, varyanslarının toplamı olmasıdır:

$\operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)=\sum _{i=1}^{n}\operatorname {Var} (X_{i}).$ ⓘ

Bu ifade Bienaymé formülü olarak adlandırılır ve 1853 yılında keşfedilmiştir. Genellikle değişkenlerin bağımsız olduğu daha güçlü bir koşulla yapılır, ancak ilişkisiz olmak yeterlidir. Dolayısıyla, tüm değişkenler aynı σ² varyansına sahipse, n ile bölme doğrusal bir dönüşüm olduğundan, bu formül hemen ortalamalarının varyansının ⓘ

$\operatorname {Var} \left({\overline {X}}\right)=\operatorname {Var} \left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)={\frac {1}{n^{2}}}\sum _{i=1}^{n}\operatorname {Var} \left(X_{i}\right)={\frac {1}{n^{2}}}n\sigma ^{2}={\frac {\sigma ^{2}}{n}}.$ ⓘ

Yani, n arttıkça ortalamanın varyansı azalır. Ortalamanın varyansı için bu formül, merkezi limit teoreminde kullanılan örnek ortalamasının standart hatasının tanımında kullanılır. ⓘ

İlk ifadeyi kanıtlamak için şunu göstermek yeterlidir ⓘ

$\operatorname {Var} (X+Y)=\operatorname {Var} (X)+\operatorname {Var} (Y).$ ⓘ

Genel sonuç tümevarım yoluyla elde edilir. Tanımdan başlayarak, ⓘ

${\begin{aligned}\operatorname {Var} (X+Y)&=\operatorname {E} \left[(X+Y)^{2}\right]-(\operatorname {E} [X+Y])^{2}\\[5pt]&=\operatorname {E} \left[X^{2}+2XY+Y^{2}\right]-(\operatorname {E} [X]+\operatorname {E} [Y])^{2}.\end{aligned}}$ ⓘ

Beklenti operatörünün doğrusallığı ve X ve Y'nin bağımsızlığı (veya ilişkisizliği) varsayımı kullanılarak, bu durum aşağıdaki gibi daha da basitleştirilir:

${\begin{aligned}\operatorname {Var} (X+Y)&=\operatorname {E} \left[X^{2}\right]+2\operatorname {E} [XY]+\operatorname {E} \left[Y^{2}\right]-\left(\operatorname {E} [X]^{2}+2\operatorname {E} [X]\operatorname {E} [Y]+\operatorname {E} [Y]^{2}\right)\\[5pt]&=\operatorname {E} \left[X^{2}\right]+\operatorname {E} \left[Y^{2}\right]-\operatorname {E} [X]^{2}-\operatorname {E} [Y]^{2}\\[5pt]&=\operatorname {Var} (X)+\operatorname {Var} (Y).\end{aligned}}$ ⓘ

İlişkili değişkenlerin toplamı

Korelasyon ve sabit örneklem büyüklüğü ile

Genel olarak, değişkenler birbirleriyle aralarında korelasyon gösteriyorlarsa, toplamlarının varyansı kovaryanslarının toplamı olur:

$\operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)=\sum _{i=1}^{n}\sum _{j=1}^{n}\operatorname {Kov} (X_{i},X_{j}).$ ⓘ

Burada Kov kovaryanstır ve eğer herhangi bir rassal değişken bağımsız ise, bu değişkenle diğer değişkenler arasında bulunan her kovaryans değeri 0 olur. Verilen formül toplamın varyansının toplamı yapan parçaların kovaryans matrisinin bütün elemanlarına eşit olduğunu göstermektedir. Bu formül klasik sınama kuramında Cronbach'in alfa ölçüsü kavramını geliştirmek için de kullanılır. ⓘ

Eğer değişkenlerin hep birbirine eğit varyansları, yani σ², varsa ve ayrı ayrı değişkenler arasındaki korelasyonların ortalama değeri ρ ise, bu halde varyansların ortalaması şöyle ifade edilir:

$\operatorname {Var} ({\overline {X}})={\frac {\sigma ^{2}}{n}}+{\frac {n-1}{n}}\rho \sigma ^{2}.$ ⓘ

Bu formüle göre ortalamanın varyansı korelasyonlar ortalaması ile birlikte artış gösterir. ⓘ

Bunun yanında, eğer değişkenler için varyans 1 değerde ise (örneğin değişken değerleri standardize edilmişlerse) o halde bu formül daha da basitleştirilip şu sekli alır:

$\operatorname {Var} ({\overline {X}})={\frac {1}{n}}+{\frac {n-1}{n}}\rho .$ ⓘ

Bu formul klasik sinama teorisinde Spearman-Brown öngörü formülü için kullanılır. Eğer korelasyonlar sabit kalırlarsa veya aynı şekilde yakınsama gösterirlerse, bu ifade, n limitte sonsuz değere yakınsama gösterdikçe, ρ değerine yakınsama gösterir. Bunun bir sonucuna göre, eşit korelasyonları olan veya yakınsama gösteren ortalama korelasyonu olan standardize edilmiş değişkenler için ortalamanın varyansı şöyle ifade edilebilir:

$\lim _{n\to \infty }\operatorname {Var} ({\overline {X}})=\rho .$

Buna göre büyük sayıda standardize edilmiş değişkenlerin ortalamasının varyansı, yaklaşık olarak bunların ortalama korelasyonuna eşittir. ⓘ

Bu formul diğer bir sonuç da ortaya çıkartır. Büyük sayılar yasası örneklem ortalamasının anakütle ortalamasına yakınsama göstereceğini önermesine rağmen, bu formülden açıktır ki, birbirine korelasyonu olan değişkenler bulunuyorsa örneklem ortalaması anakütle ortalamasına yakınsama göstermez. ⓘ

(Not: İkinci eşitlik Cov(Xi,Xi) = Var(Xi) gerçeğinden gelmektedir). ⓘ

$\operatorname {Var} \left({\overline {X}}\right)={\frac {\sigma ^{2}}{n}}+{\frac {n-1}{n}}\rho \sigma ^{2}.$ ⓘ

$\operatorname {Var} \left({\overline {X}}\right)={\frac {1}{n}}+{\frac {n-1}{n}}\rho .$ ⓘ

$\lim _{n\to \infty }\operatorname {Var} \left({\overline {X}}\right)=\rho .$ ⓘ

I.i.d. rastgele örneklem büyüklüğü ile

Bir örneklemin, bazı kriterlere göre kaç gözlemin kabul edilebilir olacağını önceden bilmeden alındığı durumlar vardır. Bu gibi durumlarda, örneklem büyüklüğü N, varyasyonu X'in varyasyonuna eklenen rastgele bir değişkendir, öyle ki,

$\operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)=\operatorname {E} \left[N\right]\operatorname {Var} (X)+\operatorname {Var} (N)\operatorname {E} \left[X\right]^{2}$

Bu da toplam varyans yasasından kaynaklanır. ⓘ

Eğer N bir Poisson dağılımına sahipse, o zaman $\operatorname {E} [N]=\operatorname {Var} (N)$ N = n tahmin edicisi ile. $\operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)$ olur $n{S_{x}}^{2}+n{\bar {X}}^{2}$ veren $\operatorname {SE} ({\bar {X}})={\sqrt {\frac {{S_{x}}^{2}+{\bar {X}}^{2}}{n}}}$ ⓘ

Doğrusal bir kombinasyonun varyansı için matris gösterimi

Tanımlamak $X$ 'nin bir sütun vektörü olarak $n$ rastgele değişkenler $X_{1},\ldots ,X_{n}$ve $c$ 'nin bir sütun vektörü olarak $n$ skaler $c_{1},\ldots ,c_{n}$. Bu yüzden, $c^{\mathsf {T}}X$ bu rastgele değişkenlerin doğrusal bir kombinasyonudur, burada $c^{\mathsf {T}}$ 'nin transpozesini gösterir. $c$. Ayrıca bırakın $\Sigma$ 'nin kovaryans matrisi olsun. $X$. Varyansı $c^{\mathsf {T}}X$ ile verilir:

$\operatorname {Var} \left(c^{\mathsf {T}}X\right)=c^{\mathsf {T}}\Sigma c.$ ⓘ

Bu, ortalamanın varyansının şu şekilde yazılabileceği anlamına gelir (birlerin sütun vektörü ile) ⓘ

$\operatorname {Var} \left({\bar {x}}\right)=\operatorname {Var} \left({\frac {1}{n}}1'X\right)={\frac {1}{n^{2}}}1'\Sigma 1.$ ⓘ

Değişkenlerin ağırlıklı toplamı

Ölçekleme özelliği ve Bienaymé formülü, kovaryans Cov(aX, bY) = ab Cov(X, Y) özelliği ile birlikte şu anlama gelir ⓘ

$\operatorname {Var} (aX\pm bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)\pm 2ab\,\operatorname {Cov} (X,Y).$ ⓘ

Bu, değişkenlerin ağırlıklı bir toplamında, en büyük ağırlığa sahip değişkenin toplamın varyansında orantısız olarak büyük bir ağırlığa sahip olacağı anlamına gelir. Örneğin, X ve Y ilişkisiz ise ve X'in ağırlığı Y'nin ağırlığının iki katı ise, X'in varyansının ağırlığı Y'nin varyansının ağırlığının dört katı olacaktır. ⓘ

Yukarıdaki ifade birden fazla değişkenin ağırlıklı toplamına genişletilebilir:

$\operatorname {Var} \left(\sum _{i}^{n}a_{i}X_{i}\right)=\sum _{i=1}^{n}a_{i}^{2}\operatorname {Var} (X_{i})+2\sum _{1\leq i}\sum _{<j\leq n}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})$ ⓘ

Bağımsız değişkenlerin çarpımı

X ve Y bağımsız iki değişken ise, bunların çarpımının varyansı şu şekilde verilir

$\operatorname {Var} (XY)=[\operatorname {E} (X)]^{2}\operatorname {Var} (Y)+[\operatorname {E} (Y)]^{2}\operatorname {Var} (X)+\operatorname {Var} (X)\operatorname {Var} (Y).$ ⓘ

Eşdeğer olarak, beklentinin temel özellikleri kullanılarak, şu şekilde verilir ⓘ

$\operatorname {Var} (XY)=\operatorname {E} \left(X^{2}\right)\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (X)]^{2}[\operatorname {E} (Y)]^{2}.$ ⓘ

İstatistiksel olarak bağımlı değişkenlerin çarpımı

Genel olarak, iki değişken istatistiksel olarak bağımlıysa, çarpımlarının varyansı şu şekilde verilir:

${\begin{aligned}\operatorname {Var} (XY)={}&\operatorname {E} \left[X^{2}Y^{2}\right]-[\operatorname {E} (XY)]^{2}\\[5pt]={}&\operatorname {Cov} \left(X^{2},Y^{2}\right)+\operatorname {E} (X^{2})\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (XY)]^{2}\\[5pt]={}&\operatorname {Cov} \left(X^{2},Y^{2}\right)+\left(\operatorname {Var} (X)+[\operatorname {E} (X)]^{2}\right)\left(\operatorname {Var} (Y)+[\operatorname {E} (Y)]^{2}\right)\\[5pt]&-[\operatorname {Cov} (X,Y)+\operatorname {E} (X)\operatorname {E} (Y)]^{2}\end{aligned}}$ ⓘ

Ayrıştırma

Varyans ayrıştırması veya toplam varyans yasası için genel formül şöyledir: Eğer $X$ ve $Y$ iki rastgele değişkendir ve varyansı $X$ varsa, o zaman ⓘ

$\operatorname {Var} [X]=\operatorname {E} (\operatorname {Var} [X\mid Y])+\operatorname {Var} (\operatorname {E} [X\mid Y]).$ ⓘ

Koşullu beklenti $\operatorname {E} (X\mid Y)$ . $X$ verilen $Y$ve koşullu varyans $\operatorname {Var} (X\mid Y)$ aşağıdaki gibi anlaşılabilir. Y rassal değişkeninin herhangi bir özel y değeri göz önüne alındığında, bir koşullu beklenti vardır $\operatorname {E} (X\mid Y=y)$ Bu miktar belirli bir y değerine bağlıdır; bir fonksiyondur $g(y)=\operatorname {E} (X\mid Y=y)$. Aynı fonksiyon Y rastgele değişkeninde değerlendirildiğinde koşullu beklentidir $\operatorname {E} (X\mid Y)=g(Y).$ ⓘ

Özellikle, eğer $Y$ olası değerler alan kesikli bir rastgele değişkendir $y_{1},y_{2},y_{3}\ldots$ karşılık gelen olasılıklarla $p_{1},p_{2},p_{3}\ldots ,$toplam varyans formülünde, sağ taraftaki ilk terim şu hale gelir ⓘ

$\operatorname {E} (\operatorname {Var} [X\mid Y])=\sum _{i}p_{i}\sigma _{i}^{2},$ ⓘ

nerede $\sigma _{i}^{2}=\operatorname {Var} [X\mid Y=y_{i}]$. Benzer şekilde, sağ taraftaki ikinci terim şu hale gelir ⓘ

$\operatorname {Var} (\operatorname {E} [X\mid Y])=\sum _{i}p_{i}\mu _{i}^{2}-\left(\sum _{i}p_{i}\mu _{i}\right)^{2}=\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2},$ ⓘ

nerede $\mu _{i}=\operatorname {E} [X\mid Y=y_{i}]$ ve $\mu =\sum _{i}p_{i}\mu _{i}$. Böylece toplam varyans şu şekilde verilir ⓘ

$\operatorname {Var} [X]=\sum _{i}p_{i}\sigma _{i}^{2}+\left(\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2}\right).$ ⓘ

Benzer bir formül varyans analizinde de uygulanır; burada ilgili formül şöyledir ⓘ

${\mathit {MS}}_{\text{total}}={\mathit {MS}}_{\text{between}}+{\mathit {MS}}_{\text{within}};$ ⓘ

Burada ${\mathit {MS}}$ Karelerin Ortalamasını ifade eder. Doğrusal regresyon analizinde ilgili formül şöyledir ⓘ

${\mathit {MS}}_{\text{total}}={\mathit {MS}}_{\text{regression}}+{\mathit {MS}}_{\text{residual}}.$ ⓘ

Bu aynı zamanda varyansların toplanabilirliğinden de türetilebilir, çünkü toplam (gözlenen) puan, tahmin edilen puan ile hata puanının toplamıdır ve son ikisi birbiriyle ilişkisizdir. ⓘ

Benzer ayrıştırmalar karesel sapmaların toplamı için de mümkündür (kareler toplamı, ${\mathit {SS}}$):

${\mathit {SS}}_{\text{total}}={\mathit {SS}}_{\text{between}}+{\mathit {SS}}_{\text{within}},$

${\mathit {SS}}_{\text{total}}={\mathit {SS}}_{\text{regression}}+{\mathit {SS}}_{\text{residual}}.$ ⓘ

CDF'den hesaplama

Negatif olmayan bir rastgele değişken için popülasyon varyansı, kümülatif dağılım fonksiyonu F cinsinden şu şekilde ifade edilebilir ⓘ

$2\int _{0}^{\infty }u(1-F(u))\,du-\left(\int _{0}^{\infty }(1-F(u))\,du\right)^{2}.$ ⓘ

Bu ifade, CDF'nin uygun bir şekilde ifade edilebildiği ancak yoğunluğun ifade edilemediği durumlarda varyansı hesaplamak için kullanılabilir. ⓘ

Karakteristik özellik

Bir rassal değişkenin ikinci momentinin minimum değeri bu moment, rassal değişkenin ortalaması etrafında alınınca ortaya çıkar; yani

$\mathrm {argmin} _{m}\,\mathrm {E} ((X-m)^{2})=\mathrm {E} (X)\,$,

Bunun aksi olarak, eğer sürekli bir fonksiyon olan $\varphi$ tüm X rassal değişkenleri için

$\mathrm {argmin} _{m}\,\mathrm {E} (\varphi (X-m))=\mathrm {E} (X)\,$

koşulunu sağlıyorsa, o halde mutlaka $\varphi (x)=ax^{2}+b$ ( a > 0) şeklinde bir fonksiyon olması gerekmektedir. Bu koşul çoklu boyutlu hallerde de geçerlidir. ⓘ

Ölçüm birimleri

Beklenen mutlak sapmanın aksine, bir değişkenin varyansı, değişkenin kendi birimlerinin karesi olan birimlere sahiptir. Örneğin, metre cinsinden ölçülen bir değişkenin varyansı metrenin karesi cinsinden ölçülür. Bu nedenle, veri setlerini standart sapma veya kök ortalama kare sapma ile tanımlamak genellikle varyans kullanmak yerine tercih edilir. Zar örneğinde standart sapma √2,9 ≈ 1,7'dir ve beklenen mutlak sapma olan 1,5'ten biraz daha büyüktür. ⓘ

Standart sapma ve beklenen mutlak sapmanın her ikisi de bir dağılımın "yayılımının" bir göstergesi olarak kullanılabilir. Standart sapma, beklenen mutlak sapmaya kıyasla cebirsel manipülasyona daha uygundur ve varyans ve onun genellemesi olan kovaryans ile birlikte teorik istatistikte sıklıkla kullanılır; ancak beklenen mutlak sapma, ölçüm anormalliklerinden veya aşırı ağır kuyruklu bir dağılımdan kaynaklanan aykırı değerlere daha az duyarlı olduğu için daha sağlam olma eğilimindedir. ⓘ

Bir fonksiyonun varyansının yaklaşık olarak hesaplanması

Delta yöntemi, bir veya daha fazla rastgele değişkenin bir fonksiyonunun varyansını yaklaşık olarak hesaplamak için ikinci dereceden Taylor açılımlarını kullanır: rastgele değişkenlerin fonksiyonlarının momentleri için Taylor açılımlarına bakınız. Örneğin, bir değişkenli bir fonksiyonun yaklaşık varyansı şu şekilde verilir ⓘ

$\operatorname {Var} \left[f(X)\right]\approx \left(f'(\operatorname {E} \left[X\right])\right)^{2}\operatorname {Var} \left[X\right]$ ⓘ

f'nin iki kez türevlenebilir olması ve X'in ortalama ve varyansının sonlu olması koşuluyla. ⓘ

Popülasyon varyansı ve örnek varyansı

Dünkü yağmurun gün boyunca ölçülmesi gibi gerçek dünya gözlemleri tipik olarak yapılabilecek tüm olası gözlemlerin tam kümesi olamaz. Bu nedenle, sonlu kümeden hesaplanan varyans, genel olarak olası gözlemlerin tam popülasyonundan hesaplanacak varyansla eşleşmeyecektir. Bu, bir tahmin edici denklem kullanarak sınırlı bir gözlem kümesinden ortalama ve varyansın tahmin edilmesi anlamına gelir. Tahmin edici, tüm olası gözlemler popülasyonundan gözlemsel yanlılık olmaksızın çekilen n gözlemlik örneklemin bir fonksiyonudur. Bu örnekte bu örnek, ilgilenilen coğrafyadaki mevcut yağmur ölçerlerden dünkü yağışların gerçek ölçümleri kümesi olacaktır. ⓘ

Popülasyon ortalaması ve popülasyon varyansı için en basit tahmin ediciler basitçe örneklemin ortalaması ve varyansı, örneklem ortalaması ve (düzeltilmemiş) örneklem varyansıdır - bunlar tutarlı tahmin edicilerdir (örneklem sayısı arttıkça doğru değere yakınsarlar), ancak geliştirilebilirler. Örneklemin varyansını alarak popülasyon varyansını tahmin etmek genel olarak optimale yakındır, ancak iki şekilde geliştirilebilir. En basit şekilde, örnek varyansı, n'ye bölünerek (örnek) ortalama hakkındaki karesel sapmaların ortalaması olarak hesaplanır. Payda için dört yaygın değer n, n - 1, n + 1 ve n - 1.5'tir: n en basit olanıdır (örneklemin popülasyon varyansı), n - 1 yanlılığı ortadan kaldırır, n + 1 normal dağılım için ortalama karesel hatayı en aza indirir ve n - 1.5 normal dağılım için standart sapmanın yansız tahmininde yanlılığı çoğunlukla ortadan kaldırır. ⓘ

İlk olarak, gerçek popülasyon ortalaması bilinmiyorsa, örnek varyansı (gerçek ortalama yerine örnek ortalamasını kullanan) yanlı bir tahmin edicidir: varyansı (n - 1) / n faktörü ile eksik tahmin eder; bu faktörle düzeltmeye (n yerine n - 1'e bölerek) Bessel düzeltmesi denir. Elde edilen tahmin edici yansızdır ve (düzeltilmiş) örnek varyansı veya yansız örnek varyansı olarak adlandırılır. Örneğin, n = 1 olduğunda, örneklem ortalaması (kendisi) hakkındaki tek bir gözlemin varyansı, popülasyon varyansından bağımsız olarak açıkça sıfırdır. Ortalama, varyansı tahmin etmek için kullanılan aynı örneklerden başka bir şekilde belirlenirse, bu yanlılık ortaya çıkmaz ve varyans güvenli bir şekilde (bağımsız olarak bilinen) ortalama hakkındaki örneklerin varyansı olarak tahmin edilebilir. ⓘ

İkinci olarak, örnek varyansı genellikle örnek varyansı ile popülasyon varyansı arasındaki ortalama karesel hatayı minimize etmez. Yanlılığın düzeltilmesi genellikle bu durumu daha da kötüleştirir: her zaman düzeltilmiş örnek varyansından daha iyi performans gösteren bir ölçek faktörü seçilebilir, ancak optimum ölçek faktörü popülasyonun aşırı basıklığına bağlıdır (bkz. ortalama karesel hata: varyans) ve yanlılık getirir. Bu her zaman yansız tahmin edicinin küçültülmesinden (n - 1'den daha büyük bir sayıya bölünmesi) oluşur ve büzülme tahmin edicisinin basit bir örneğidir: yansız tahmin edici sıfıra doğru "küçültülür". Normal dağılım için, n + 1'e bölmek (n - 1 veya n yerine) ortalama karesel hatayı en aza indirir. Ancak ortaya çıkan tahminci yanlıdır ve yanlı örnek varyasyonu olarak bilinir. ⓘ

Nüfus varyansı

Genel olarak, xi değerlerine sahip N büyüklüğündeki sonlu bir popülasyonun popülasyon varyansı şu şekilde verilir ⓘ

$${\begin{aligned}\sigma ^{2}&={\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}-\mu \right)^{2}={\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}^{2}-2\mu x_{i}+\mu ^{2}\right)\\[5pt]&=\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-2\mu \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)+\mu ^{2}\\[5pt]&=\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-\mu ^{2}\end{aligned}}$$

ⓘ

burada popülasyon ortalaması ⓘ

$\mu ={\frac {1}{N}}\sum _{i=1}^{N}x_{i}.$ ⓘ

Popülasyon varyansı şu şekilde de hesaplanabilir ⓘ

$\sigma ^{2}={\frac {1}{N^{2}}}\sum _{i<j}\left(x_{i}-x_{j}\right)^{2}={\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}-x_{j}\right)^{2}.$ ⓘ

Bu doğrudur çünkü ⓘ

$${\begin{aligned}&{\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}-x_{j}\right)^{2}\\[5pt]={}&{\frac {1}{2N^{2}}}\sum _{i,j=1}^{N}\left(x_{i}^{2}-2x_{i}x_{j}+x_{j}^{2}\right)\\[5pt]={}&{\frac {1}{2N}}\sum _{j=1}^{N}\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}^{2}\right)-\left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)\left({\frac {1}{N}}\sum _{j=1}^{N}x_{j}\right)+{\frac {1}{2N}}\sum _{i=1}^{N}\left({\frac {1}{N}}\sum _{j=1}^{N}x_{j}^{2}\right)\\[5pt]={}&{\frac {1}{2}}\left(\sigma ^{2}+\mu ^{2}\right)-\mu ^{2}+{\frac {1}{2}}\left(\sigma ^{2}+\mu ^{2}\right)\\[5pt]={}&\sigma ^{2}\end{aligned}}$$

ⓘ

Popülasyon varyansı, üreten olasılık dağılımının varyansıyla eşleşir. Bu anlamda, popülasyon kavramı sonsuz popülasyonlu sürekli rastgele değişkenlere genişletilebilir. ⓘ

Önyargılı örnek varyansı

Birçok pratik durumda, bir popülasyonun gerçek varyansı önceden bilinmez ve bir şekilde hesaplanması gerekir. Çok büyük popülasyonlarla uğraşırken, popülasyondaki her nesneyi saymak mümkün değildir, bu nedenle hesaplama popülasyonun bir örneği üzerinde yapılmalıdır. Örnek varyans, sürekli bir dağılımın varyansının bu dağılımın bir örneğinden tahmin edilmesine de uygulanabilir. ⓘ

Popülasyondan n < N olmak üzere n adet Y₁, ..., Yn değerini değiştirerek bir örnek alırız ve bu örneğe dayanarak varyansı tahmin ederiz. Örnek verilerin varyansını doğrudan almak, karesel sapmaların ortalamasını verir:

${\tilde {S}}_{Y}^{2}={\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}=\left({\frac {1}{n}}\sum _{i=1}^{n}Y_{i}^{2}\right)-{\overline {Y}}^{2}={\frac {1}{n^{2}}}\sum _{i,j\,:\,i<j}\left(Y_{i}-Y_{j}\right)^{2}.$ ⓘ

Burada, ${\overline {Y}}$ örnek ortalamasını gösterir:

${\overline {Y}}={\frac {1}{n}}\sum _{i=1}^{n}Y_{i}.$ ⓘ

Yi rastgele seçildiğinden, her iki ${\overline {Y}}$ ve ${\tilde {S}}_{Y}^{2}$ rastgele değişkenlerdir. Bunların beklenen değerleri, popülasyondan alınan n büyüklüğündeki tüm olası örneklerin {Yi} ortalaması alınarak değerlendirilebilir. İçin ${\tilde {S}}_{Y}^{2}$ bu verir:

${\begin{aligned}\operatorname {E} [{\tilde {S}}_{Y}^{2}]&=\operatorname {E} \left[{\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\frac {1}{n}}\sum _{j=1}^{n}Y_{j}\right)^{2}\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\operatorname {E} \left[Y_{i}^{2}-{\frac {2}{n}}Y_{i}\sum _{j=1}^{n}Y_{j}+{\frac {1}{n^{2}}}\sum _{j=1}^{n}Y_{j}\sum _{k=1}^{n}Y_{k}\right]\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\left({\frac {n-2}{n}}\operatorname {E} \left[Y_{i}^{2}\right]-{\frac {2}{n}}\sum _{j\neq i}\operatorname {E} \left[Y_{i}Y_{j}\right]+{\frac {1}{n^{2}}}\sum _{j=1}^{n}\sum _{k\neq j}^{n}\operatorname {E} \left[Y_{j}Y_{k}\right]+{\frac {1}{n^{2}}}\sum _{j=1}^{n}\operatorname {E} \left[Y_{j}^{2}\right]\right)\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}\left[{\frac {n-2}{n}}\left(\sigma ^{2}+\mu ^{2}\right)-{\frac {2}{n}}(n-1)\mu ^{2}+{\frac {1}{n^{2}}}n(n-1)\mu ^{2}+{\frac {1}{n}}\left(\sigma ^{2}+\mu ^{2}\right)\right]\\[5pt]&={\frac {n-1}{n}}\sigma ^{2}.\end{aligned}}$ ⓘ

Dolayısıyla ${\tilde {S}}_{Y}^{2}$ 'lik bir katsayı ile yanlı olan popülasyon varyansının bir tahminini verir. ${\frac {n-1}{n}}$. Bu nedenle, ${\tilde {S}}_{Y}^{2}$ yanlı örneklem varyansı olarak adlandırılır. ⓘ

Yansız örneklem varyansı

Bu yanlılığın düzeltilmesi, yansız örnek varyansını verir ve şu şekilde gösterilir $S^{2}$:

$S^{2}={\frac {n}{n-1}}{\tilde {S}}_{Y}^{2}={\frac {n}{n-1}}\left[{\frac {1}{n}}\sum _{i=1}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}\right]={\frac {1}{n-1}}\sum _{i=1}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}$ ⓘ

Versiyonu bağlam tarafından belirlenebildiğinde, her iki tahmin edici de basitçe örnek varyansı olarak adlandırılabilir. Aynı kanıt, sürekli bir olasılık dağılımından alınan örnekler için de geçerlidir. ⓘ

n - 1 teriminin kullanımı Bessel düzeltmesi olarak adlandırılır ve örneklem kovaryansında ve örneklem standart sapmasında (varyansın karekökü) da kullanılır. Karekök içbükey bir fonksiyondur ve bu nedenle dağılıma bağlı olan negatif yanlılık (Jensen eşitsizliği ile) getirir ve bu nedenle düzeltilmiş örneklem standart sapması (Bessel düzeltmesi kullanılarak) yanlıdır. Standart sapmanın yansız tahmini teknik olarak karmaşık bir sorundur, ancak normal dağılım için n - 1,5 terimini kullanmak neredeyse yansız bir tahminci verir. ⓘ

Yansız örneklem varyansı, ƒ(y₁, y₂) = (y₁ - y₂)²/2 fonksiyonu için bir U-istatistiğidir, yani popülasyonun 2 elemanlı alt kümeleri üzerinde 2 örneklemli bir istatistiğin ortalaması alınarak elde edilir. ⓘ

Örnek varyansının dağılımı

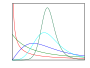
yi bağımsız normal dağılımlı olduğunda, ν = n - 1'in çeşitli değerleri için S²/σ²'nin dağılımı ve kümülatif dağılımı.

Rastgele değişkenlerin bir fonksiyonu olan örnek varyansının kendisi de bir rastgele değişkendir ve dağılımını incelemek doğaldır. Yi'nin normal dağılımdan bağımsız gözlemler olduğu durumda, Cochran teoremi S²'n_in ölçeklendirilmiş ki-kare dağılımını izlediğini gösterir:

$(n-1){\frac {S^{2}}{\sigma ^{2}}}\sim \chi _{n-1}^{2}.$ ⓘ

Bunun doğrudan bir sonucu olarak

$\operatorname {E} \left(S^{2}\right)=\operatorname {E} \left({\frac {\sigma ^{2}}{n-1}}\chi _{n-1}^{2}\right)=\sigma ^{2},$ ⓘ

ve ⓘ

$\operatorname {Var} \left[S^{2}\right]=\operatorname {Var} \left({\frac {\sigma ^{2}}{n-1}}\chi _{n-1}^{2}\right)={\frac {\sigma ^{4}}{(n-1)^{2}}}\operatorname {Var} \left(\chi _{n-1}^{2}\right)={\frac {2\sigma ^{4}}{n-1}}.$ ⓘ

Yi'ler bağımsız ve aynı dağılıma sahipse, ancak normal dağılıma sahip olmaları gerekmiyorsa ⓘ

$\operatorname {E} \left[S^{2}\right]=\sigma ^{2},\quad \operatorname {Var} \left[S^{2}\right]={\frac {\sigma ^{4}}{n}}\left(\kappa -1+{\frac {2}{n-1}}\right)={\frac {1}{n}}\left(\mu _{4}-{\frac {n-3}{n-1}}\sigma ^{4}\right),$ ⓘ

Burada κ dağılımın basıklığı ve μ₄ dördüncü merkezi momenttir. ⓘ

Kareli gözlemler için büyük sayılar kanunu koşulları geçerliyse, S² σ²'nin tutarlı bir tahmincisidir. Gerçekten de tahmin edicinin varyansının asimptotik olarak sıfıra yöneldiği görülebilir. Asimptotik olarak eşdeğer bir formül Kenney ve Keeping (1951:164), Rose ve Smith (2002:264) ve Weisstein'da (t.y.) verilmiştir. ⓘ

Samuelson'un eşitsizliği

Samuelson eşitsizliği, örneklem ortalaması ve (yanlı) varyansın hesaplanmış olduğu göz önüne alındığında, bir örneklemdeki bireysel gözlemlerin alabileceği değerler üzerindeki sınırları belirten bir sonuçtur. Değerler sınırlar içinde kalmalıdır ${\bar {y}}\pm \sigma _{Y}(n-1)^{1/2}.$ ⓘ

Harmonik ve aritmetik ortalama ile ilişkiler

Pozitif reel sayılardan oluşan bir {yi} örneği için gösterilmiştir, ⓘ

$\sigma _{y}^{2}\leq 2y_{\max }(A-H),$ ⓘ

Burada y_max örneklemin maksimum değeri, A aritmetik ortalama, H örneklemin harmonik ortalaması ve $\sigma _{y}^{2}$ örneklemin (yanlı) varyansıdır. ⓘ

Bu sınır geliştirilmiştir ve varyansın şu şekilde sınırlandığı bilinmektedir ⓘ

$\sigma _{y}^{2}\leq {\frac {y_{\max }(A-H)(y_{\max }-A)}{y_{\max }-H}},$ ⓘ

$\sigma _{y}^{2}\geq {\frac {y_{\min }(A-H)(A-y_{\min })}{H-y_{\min }}},$ ⓘ

burada ymin örneklemin minimum değeridir. ⓘ

Dış kaynaklar

• Spiegel, Murray R, ve Stephens, Larry J. (Tr.Çev.: Çelebioğlu, Salih) (2013) İstatistik , İstanbul: Nobel Akademik Yayıncılık ISBN 9786051337043 ⓘ

İki veya daha fazla varyansın eşitliğini test etmek zordur. F testi ve ki kare testlerinin her ikisi de normal olmama durumundan olumsuz etkilenir ve bu amaç için önerilmez. ⓘ

Çeşitli parametrik olmayan testler önerilmiştir: bunlar arasında Barton-David-Ansari-Freund-Siegel-Tukey testi, Capon testi, Mood testi, Klotz testi ve Sukhatme testi bulunmaktadır. Sukhatme testi iki varyans için geçerlidir ve her iki medyanın da bilinmesini ve sıfıra eşit olmasını gerektirir. Mood, Klotz, Capon ve Barton-David-Ansari-Freund-Siegel-Tukey testleri de iki varyans için geçerlidir. Bu testler ortancanın bilinmemesine izin verir ancak iki ortancanın eşit olmasını gerektirir. ⓘ

Lehmann testi, iki varyansın parametrik bir testidir. Bu testin bilinen birkaç çeşidi vardır. Varyansların eşitliğine ilişkin diğer testler arasında Box testi, Box-Anderson testi ve Moses testi yer almaktadır. ⓘ

Varyansların eşitliğini test etmek için bootstrap ve jackknife gibi yeniden örnekleme yöntemleri kullanılabilir. ⓘ

Tarihçe

Varyans terimi ilk kez Ronald Fisher tarafından 1918 tarihli The Correlation Between Relatives on the Supposition of Mendelian Inheritance adlı makalesinde kullanılmıştır:

Mevcut istatistiklerin büyük bir kısmı bize, bir insan ölçümünün ortalamasından sapmalarının Normal Hata Yasasını çok yakından takip ettiğini ve bu nedenle değişkenliğin, ortalama karesel hatanın kareköküne karşılık gelen standart sapma ile düzgün bir şekilde ölçülebileceğini göstermektedir. Normalde tek tip olan bir popülasyonda standart sapmalara sahip dağılımlar üretebilen iki bağımsız değişkenlik nedeni olduğunda $\sigma _{1}$ ve $\sigma _{2}$dağılımının, her iki neden birlikte hareket ettiğinde, standart sapmaya sahip olduğu bulunmuştur ${\sqrt {\sigma _{1}^{2}+\sigma _{2}^{2}}}$. Bu nedenle, değişkenliğin nedenlerini analiz ederken, değişkenliğin ölçüsü olarak standart sapmanın karesi ile ilgilenmek arzu edilir. Bu niceliği Varyans olarak adlandıracağız... ⓘ

Rastgele bir dağılımın varyansının geometrik görselleştirmesi (2, 4, 4, 4, 5, 5, 7, 9):

1. Bir frekans dağılımı oluşturulur.
2. Dağılımın merkez noktası ortalamasını verir.
3. Her değer için, kenarları her değerin ortalamadan farkına eşit olan bir kare oluşturulur.
4. Kareler, bir kenarı değer sayısına (n) eşit olan bir dikdörtgen şeklinde düzenlendiğinde, diğer kenar dağılımın varyansı (σ²) olur. ⓘ

Eylemsizlik momenti

Bir olasılık dağılımının varyansı, kütle merkezi etrafında dönmeye göre bir doğru boyunca karşılık gelen bir kütle dağılımının klasik mekanikteki eylemsizlik momentine benzer. Bu analoji nedeniyle varyans gibi şeylere olasılık dağılımlarının momentleri denir. Kovaryans matrisi, çok değişkenli dağılımlar için eylemsizlik momenti tensörü ile ilişkilidir. Kovaryans matrisi aşağıdaki gibi olan n noktadan oluşan bir bulutun atalet momenti $\Sigma$ tarafından verilir

$I=n\left(\mathbf {1} _{3\times 3}\operatorname {tr} (\Sigma )-\Sigma \right).$ ⓘ

Fizikteki ve istatistikteki eylemsizlik momenti arasındaki bu fark, bir doğru boyunca toplanan noktalar için açıktır. Birçok noktanın x eksenine yakın olduğunu ve bu eksen boyunca dağıldığını varsayalım. Kovaryans matrisi şöyle görünebilir

$\Sigma ={\begin{bmatrix}10&0&0\\0&0.1&0\\0&0&0.1\end{bmatrix}}.$ ⓘ

Yani, x yönünde en fazla varyans vardır. Fizikçiler bunun x ekseni etrafında düşük bir momente sahip olduğunu düşünürler, bu nedenle eylemsizlik momenti tensörü

$I=n{\begin{bmatrix}0.2&0&0\\0&10.1&0\\0&0&10.1\end{bmatrix}}.$ ⓘ

Yarı Değişkenlik

Yarıvaryans, varyans ile aynı şekilde hesaplanır ancak sadece ortalamanın altında kalan gözlemler hesaplamaya dahil edilir:

$${\text{Semivariance}}={1 \over {n}}\sum _{i:x_{i}<\mu }(x_{i}-\mu )^{2}$$

Farklı uygulama alanlarında özel bir ölçü olarak da tanımlanmaktadır. Çarpık dağılımlar için yarıvaryans, varyansın sağlamadığı ek bilgileri sağlayabilir. ⓘ

Yarıvaryans ile ilişkili eşitsizlikler için Chebyshev eşitsizliği § Yarıvaryanslar bölümüne bakınız. ⓘ

Genelleştirmeler

Karmaşık değişkenler için

Eğer $x$ 'de değerleri olan skaler karmaşık değerli bir rastgele değişkendir. $\mathbb {C} ,$ o zaman varyansı $\operatorname {E} \left[(x-\mu )(x-\mu )^{*}\right],$ nerede $x^{*}$ 'nin karmaşık eşleniğidir. $x.$ Bu varyans gerçek bir skalerdir. ⓘ

Vektör değerli rassal değişkenler için

Bir matris olarak

Eğer $X$ 'de değerleri olan vektör değerli bir rastgele değişkendir. $\mathbb {R} ^{n},$ ve bir sütun vektörü olarak düşünüldüğünde, varyansın doğal bir genellemesi $\operatorname {E} \left[(X-\mu )(X-\mu )^{\operatorname {T} }\right],$ nerede $\mu =\operatorname {E} (X)$ ve $X^{\operatorname {T} }$ 'nin transpozesidir. $X,$ ve dolayısıyla bir satır vektörüdür. Sonuç, genellikle varyans-kovaryans matrisi (veya sadece kovaryans matrisi) olarak adlandırılan pozitif yarı tanımlı bir kare matristir. ⓘ

Eğer $X$ 'de değerleri olan vektör ve karmaşık değerli bir rastgele değişkendir. $\mathbb {C} ^{n},$ o zaman kovaryans matrisi $\operatorname {E} \left[(X-\mu )(X-\mu )^{\dagger }\right],$ nerede $X^{\dagger }$ 'nin eşlenik transpozesidir. $X.$ Bu matris aynı zamanda pozitif yarı tanımlı ve karedir. ⓘ

Bir skaler olarak

Vektör değerli rastgele değişkenler için varyansın bir başka genellemesi $X$matris yerine skaler bir değerle sonuçlanan genelleştirilmiş varyanstır. $\det(C)$kovaryans matrisinin determinantıdır. Genelleştirilmiş varyansın, noktaların ortalamaları etrafındaki çok boyutlu dağılımıyla ilişkili olduğu gösterilebilir. ⓘ

Rassal değişken ile ortalaması arasındaki Öklid uzaklığı dikkate alınarak farklı bir genelleme elde edilir. Bu şu sonuçları verir $\operatorname {E} \left[(X-\mu )^{\operatorname {T} }(X-\mu )\right]=\operatorname {tr} (C),$ Bu da kovaryans matrisinin izidir. ⓘ

Formüller

Örnekler

Varyans; verilerin aritmetik ortalamadan sapmalarının karelerinin aritmetik ortalaması olduğuna göre, ⓘ

2,2,3,5,3 serisinin varyansı şu şekilde bulunur; ⓘ

1) Verilerin aritmetik ortalaması (A.O) hesaplanır.

$\operatorname {A} .O={\frac {(2+2+3+5+3)}{5}}=3$

2) 1. maddedeki ortalamadan,verilerin sapmalarının karelerinin aritmetik ortalaması alınarak varyans bulunur.

$\operatorname {\frac {[(2-3)^{2}+(2-3)^{2}+(3-3)^{2}+(5-3)^{2}+(3-3)^{2}]}{5}} ={\frac {6}{5}}$ ⓘ

Örneğin 1: Tablo ile verilmiş bir aralıklı deneysel dağılım

Bu örnekte bir X rastlantı değişkeninin i=1,2,3 için aldığı değerler ve X in bu değerleri alması olasılığı bir tablo olarak verilmiştir. ⓘ

i	1	2	3 ⓘ
xi	-1	1	2
f(xi)	0,5	0,3	0,2

Beklenen değer şöyle hesaplanır:

$\operatorname {E} (X)=-1\cdot 0{,}5+1\cdot 0{,}3+2\cdot 0{,}2=0{,}2$ ⓘ

Genel formülle, varyans şöyle bulunur:

$\operatorname {Var} (X)=(-1-0{,}2)^{2}\cdot 0{,}5+(1-0{,}2)^{2}\cdot 0{,}3+(2-0{,}2)^{2}\cdot 0{,}2=1{,}56$ ⓘ

Hesaplama formülu ile ise varyans şöyle hesaplanır ve aynı sonuç verir:

$\operatorname {Var} (X)=(-1)^{2}\cdot 0{,}5+1^{2}\cdot 0{,}3+2^{2}\cdot 0{,}2-0{,}2^{2}=1{,}56.$ ⓘ

Varyansın biçimsel özellikleri

Varyansın şu özellikleri bulunmaktadır: ⓘ

Varyans için hesaplama formülü

Varyans için hesaplama formülü hemen doğrudan doğruya beklenen değerlerin doğrusallarından ve yukarıda verilen tanımlamadan ortaya çıkar\; ⓘ

${}\operatorname {Var} (X)=\operatorname {E} (X^{2}-2\,X\,\operatorname {E} (X)+(\operatorname {E} (X))^{2}),$ ⓘ

${}=\operatorname {E} (X^{2})-2(\operatorname {E} (X))^{2}+(\operatorname {E} (X))^{2},$ ⓘ

${}=\operatorname {E} (X^{2})-(\operatorname {E} (X))^{2}.$ ⓘ

Bu çok zaman pratikte varyans hesaplaması için kullanılır. Fakat eğer denklemin iki kısmının değerleri birbirine eşit veya çok yakınsa numerik yaklaşımlama hatasından etkilenip yanlış değerler verebilir. ⓘ