Polarizasyon

Kauçuk iplik üzerinde dairesel polarizasyon, doğrusal polarizasyona dönüştürüldü ⓘ

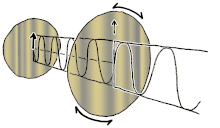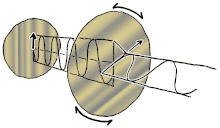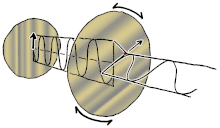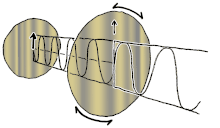
Polarizasyon (ayrıca kutuplaşma), salınımların geometrik yönelimini belirten enine dalgalara uygulanan bir özelliktir. Enine bir dalgada, salınımın yönü dalganın hareket yönüne diktir. Polarize enine dalganın basit bir örneği, gergin bir tel boyunca ilerleyen titreşimlerdir (resme bakın); örneğin gitar teli gibi bir müzik aletinde. Telin nasıl koparıldığına bağlı olarak, titreşimler dikey yönde, yatay yönde veya tele dik herhangi bir açıda olabilir. Buna karşılık, bir sıvı veya gazdaki ses dalgaları gibi uzunlamasına dalgalarda, salınımdaki parçacıkların yer değiştirmesi her zaman yayılma yönündedir, bu nedenle bu dalgalar polarizasyon göstermez. Polarizasyon sergileyen enine dalgalar arasında ışık ve radyo dalgaları gibi elektromanyetik dalgalar, yerçekimi dalgaları ve katılardaki enine ses dalgaları (kesme dalgaları) bulunur. ⓘ

Işık gibi bir elektromanyetik dalga, her zaman birbirine dik olan birleşik salınımlı elektrik alanı ve manyetik alandan oluşur; geleneksel olarak, elektromanyetik dalgaların "polarizasyonu" elektrik alanının yönünü ifade eder. Doğrusal polarizasyonda, alanlar tek bir yönde salınır. Dairesel veya eliptik polarizasyonda, alanlar dalga ilerlerken bir düzlemde sabit bir oranda döner. Dönmenin iki olası yönü olabilir; eğer alanlar dalganın hareket yönüne göre sağa doğru dönüyorsa buna sağ dairesel polarizasyon, eğer alanlar sola doğru dönüyorsa buna da sol dairesel polarizasyon denir. ⓘ

Güneş, alevler ve akkor lambalar gibi birçok kaynaktan gelen ışık veya diğer elektromanyetik radyasyon, polarizasyonların eşit bir karışımına sahip kısa dalga trenlerinden oluşur; buna polarize olmayan ışık denir. Polarize ışık, polarize olmayan ışığın sadece bir polarizasyona sahip dalgaların geçmesine izin veren bir polarizörden geçirilmesiyle üretilebilir. En yaygın optik malzemeler ışığın polarizasyonunu etkilemez, ancak bazı malzemeler - çift kırılma, dikroizm veya optik aktivite sergileyenler - ışığı polarizasyonuna bağlı olarak farklı şekilde etkiler. Bunlardan bazıları polarize filtreler yapmak için kullanılır. Işık ayrıca bir yüzeyden belli bir açıyla yansıdığında da kısmen polarize olur. ⓘ

Kuantum mekaniğine göre, elektromanyetik dalgalar foton adı verilen parçacık akımları olarak da görülebilir. Bu şekilde bakıldığında, bir elektromanyetik dalganın polarizasyonu, fotonların spin adı verilen kuantum mekaniksel bir özelliği tarafından belirlenir. Bir foton iki olası spinden birine sahiptir: hareket yönüne göre ya sağa doğru ya da sola doğru dönebilir. Dairesel olarak kutuplanmış elektromanyetik dalgalar, sağ ya da sol el olmak üzere yalnızca bir tür spine sahip fotonlardan oluşur. Doğrusal polarize dalgalar, bir düzlemde salınım vermek üzere senkronize edilmiş eşit genlik ve fazlara sahip sağ ve sol dairesel polarize durumların süperpozisyonunda bulunan fotonlardan oluşur. ⓘ

Polarizasyon, optik, sismoloji, radyo ve mikrodalgalar gibi enine dalgalarla ilgilenen bilim alanlarında önemli bir parametredir. Özellikle lazerler, kablosuz ve fiber optik telekomünikasyon ve radar gibi teknolojiler bundan etkilenmektedir. ⓘ

Polarizasyon terimi dolayısıyla yansıyan dalga yoluna dik gelen düzlemdeki salınım işleminin olası yönlenmelerini ifade eder. ⓘ

Polarizasyon çeşitleri:

Linear polarization diagram

Çizgisel-Linear

Circular polarization diagram

Dairesel-Circular

Elliptical polarization diagram

Eliptik-Elliptical ⓘ

Giriş

Dalga yayılımı ve polarizasyon

çapraz doğrusal polarize ⓘ

Çoğu ışık kaynağı tutarsız ve polarize olmamış (veya sadece "kısmen polarize") olarak sınıflandırılır çünkü farklı uzaysal özelliklere, frekanslara (dalga boyları), fazlara ve polarizasyon durumlarına sahip dalgaların rastgele bir karışımından oluşurlar. Bununla birlikte, elektromanyetik dalgaları ve özellikle polarizasyonu anlamak için, sadece tutarlı düzlem dalgaları düşünmek daha kolaydır; bunlar belirli bir yön (veya dalga vektörü), frekans, faz ve polarizasyon durumuna sahip sinüzoidal dalgalardır. Verilen parametrelerle bir düzlem dalgaya göre bir optik sistemi karakterize etmek daha sonra daha genel bir duruma tepkisini tahmin etmek için kullanılabilir, çünkü belirli bir uzaysal yapıya sahip bir dalga düzlem dalgaların bir kombinasyonuna (açısal spektrum olarak adlandırılır) ayrıştırılabilir. Tutarsız durumlar, frekansların (spektrumu), fazların ve polarizasyonların bazı dağılımları ile bu tür ilişkisiz dalgaların ağırlıklı bir kombinasyonu olarak stokastik olarak modellenebilir. ⓘ

Enine elektromanyetik dalgalar

Dalga boyu λ olan "dikey polarize" bir elektromanyetik dalganın elektrik alan vektörü E (kırmızı) dikey yönde salınım yapar. Manyetik alan B (veya H) her zaman ona dik açı yapar (mavi) ve her ikisi de yayılma yönüne (z) diktir. ⓘ

Boş uzayda veya başka bir homojen izotropik zayıflatmayan ortamda hareket eden elektromanyetik dalgalar (ışık gibi) enine dalgalar olarak tanımlanır, yani bir düzlem dalganın elektrik alan vektörü E ve manyetik alan H'nin her biri dalganın yayılma yönüne dik (veya "enine") bir yöndedir; E ve H aynı zamanda birbirlerine de diktir. Geleneksel olarak, bir elektromanyetik dalganın "polarizasyon" yönü elektrik alan vektörü tarafından verilir. Optik frekansı f olan monokromatik bir düzlem dalgayı (vakum dalga boyu λ olan ışık f = c/λ frekansına sahiptir, burada c ışık hızıdır) göz önünde bulundurarak, yayılma yönünü z ekseni olarak alalım. Enine bir dalga olan E ve H alanları sadece x ve y yönlerinde bileşenler içermelidir, Ez = Hz = 0. Karmaşık (veya fazör) gösterim kullanılarak, anlık fiziksel elektrik ve manyetik alanlar aşağıdaki denklemlerde yer alan karmaşık büyüklüklerin gerçek kısımları ile verilir. Zaman t ve uzaysal konum z'nin bir fonksiyonu olarak (+z yönündeki bir düzlem dalga için alanların x veya y'ye bağımlılığı olmadığından) bu karmaşık alanlar şu şekilde yazılabilir:

${\vec {E}}(z,t)={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{\lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$ ⓘ

ve

${\vec {H}}(z,t)={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{\lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$ ⓘ

Burada λ = λ₀/n ortamdaki dalga boyu (kırılma indisi n olan) ve T = 1/f dalganın periyodudur. Burada ex, ey, hx ve hy karmaşık sayılardır. Bu denklemlerin geleneksel olarak ifade edildiği ikinci daha kompakt formda, bu faktörler dalga sayısı kullanılarak tanımlanır $k=2\pi n/\lambda _{0}$ ve açısal frekans (veya "radyan frekansı") $\omega =2\pi f$. Yayılımın +z yönü ile sınırlı olmadığı daha genel bir formülasyonda, kz uzaysal bağımlılığı şu şekilde değiştirilir ${\vec {k}}\cdot {\vec {r}}$ nerede ${\vec {k}}$ dalga vektörü olarak adlandırılır ve büyüklüğü dalga sayısıdır. ⓘ

Böylece e ve h öncü vektörlerinin her biri dalganın x ve y polarizasyon bileşenlerinin genlik ve fazını tanımlayan iki sıfır olmayan (karmaşık) bileşen içerir (yine, +z yönünde enine bir dalga için z polarizasyon bileşeni olamaz). Karakteristik empedansı olan belirli bir ortam için $\eta$h, e ile ilişkilidir:

$h_{y}={\frac {e_{x}}{\eta }}$ ⓘ

ve

$h_{x}=-{\frac {e_{y}}{\eta }}$. ⓘ

Bir dielektrikte η reeldir ve η₀/n değerine sahiptir, burada n kırılma indisi ve η₀ serbest uzayın empedansıdır. İletken bir ortamda empedans karmaşık olacaktır. Bu ilişki göz önüne alındığında, E ve H'nin nokta çarpımının sıfır olması gerektiğine dikkat edin:

${\vec {E}}\left({\vec {r}},t\right)\cdot {\vec {H}}\left({\vec {r}},t\right)=e_{x}h_{x}+e_{y}h_{y}+e_{z}h_{z}=e_{x}\left(-{\frac {e_{y}}{\eta }}\right)+e_{y}\left({\frac {e_{x}}{\eta }}\right)+0\cdot 0=0$ ⓘ

Bu da beklendiği gibi bu vektörlerin ortogonal (birbirlerine dik açılı) olduğunu gösterir. ⓘ

Dolayısıyla, yayılma yönünü (bu durumda +z) ve η'yi bilerek, dalgayı sadece elektrik alanını tanımlayan ex ve ey terimleriyle de belirtebiliriz. Ex ve ey'yi içeren vektör (ancak enine bir dalga için zorunlu olarak sıfır olan z bileşeni olmadan) Jones vektörü olarak bilinir. Dalganın polarizasyon durumunu belirtmenin yanı sıra, genel bir Jones vektörü aynı zamanda bu dalganın genel büyüklüğünü ve fazını da belirtir. Spesifik olarak, ışık dalgasının yoğunluğu iki elektrik alan bileşeninin karesel büyüklüklerinin toplamıyla orantılıdır:

$I=\left(\left|e_{x}\right|^{2}+\left|e_{y}\right|^{2}\right)\,{\frac {1}{2\eta }}$ ⓘ

Ancak dalganın polarizasyon durumu sadece ey'nin ex'ye olan (karmaşık) oranına bağlıdır. Bu yüzden sadece |ex|² + |ey|² = 1 olan dalgaları ele alalım; bu, boş uzayda metrekare başına yaklaşık .00133 watt'lık bir yoğunluğa karşılık gelir (burada $\eta =$ $\eta _{0}$). Bir dalganın mutlak fazı polarizasyon durumunu tartışırken önemsiz olduğundan, ex'nin fazının sıfır olduğunu, başka bir deyişle ex'nin reel bir sayı olduğunu, ey'nin ise karmaşık olabileceğini belirtelim. Bu kısıtlamalar altında, ex ve ey aşağıdaki gibi gösterilebilir:

$e_{x}={\sqrt {\frac {1+Q}{2}}}$

$e_{y}={\sqrt {\frac {1-Q}{2}}}\,e^{i\phi }$ ⓘ

Burada polarizasyon durumu artık Q değeri (-1 < Q < 1 olacak şekilde) ve göreceli faz ile tamamen parametrelendirilmiştir $\phi$. ⓘ

Enine olmayan dalgalar

Enine dalgalara ek olarak, salınımın yayılma yönüne dik yönlerle sınırlı olmadığı birçok dalga hareketi vardır. Bu durumlar, enine dalgalara (yığın ortamdaki çoğu elektromanyetik dalga gibi) odaklanan mevcut makalenin kapsamının çok ötesindedir, ancak tutarlı bir dalganın polarizasyonunun, az önce yaptığımız gibi basitçe bir Jones vektörü kullanılarak tanımlanamayacağı durumların farkında olunmalıdır. ⓘ

Sadece elektromanyetik dalgalar göz önüne alındığında, önceki tartışmanın kesinlikle homojen izotropik zayıflatmayan bir ortamdaki düzlem dalgalar için geçerli olduğunu, oysa anizotropik bir ortamda (aşağıda tartışıldığı gibi çift kırılımlı kristaller gibi) elektrik veya manyetik alanın hem boylamsal hem de enine bileşenlere sahip olabileceğini not ediyoruz. Bu durumlarda elektriksel yer değiştirme D ve manyetik akı yoğunluğu B hala yukarıdaki geometriye uymaktadır, ancak şimdi bir tensörle verilen elektrik duyarlılığındaki (veya manyetik geçirgenlikteki) anizotropi nedeniyle, E'nin (veya H'nin) yönü D'ninkinden (veya B'ninkinden) farklı olabilir. İzotropik ortamlarda bile, kırılma indisi metaller gibi önemli bir hayali kısma (veya "sönme katsayısına") sahip olan bir ortama homojen olmayan dalgalar fırlatılabilir; bu alanlar da kesinlikle enine değildir. Bir dalga kılavuzunda (optik fiber gibi) yayılan yüzey dalgaları veya dalgalar genellikle enine dalgalar değildir, ancak bir elektrik veya manyetik enine mod veya bir hibrit mod olarak tanımlanabilir. ⓘ

Serbest uzayda bile, düzlem dalga yaklaşımının bozulduğu odak bölgelerinde boylamsal alan bileşenleri üretilebilir. Bunun uç bir örneği, odak noktasında sırasıyla elektrik veya manyetik alanın tamamen boylamasına (yayılma yönü boyunca) olduğu radyal veya teğetsel polarize ışıktır. ⓘ

Sıvılardaki ses dalgaları gibi uzunlamasına dalgalar için, salınım yönü tanımı gereği hareket yönü boyuncadır, bu nedenle polarizasyon konusundan normalde bahsedilmez bile. Öte yandan, bir kütle katı içindeki ses dalgaları, toplam üç polarizasyon bileşeni için boylamsal olduğu kadar enine de olabilir. Bu durumda, enine polarizasyon kayma gerilmesinin yönü ve yayılma yönüne dik yönlerdeki yer değiştirme ile ilişkilendirilirken, boyuna polarizasyon katının sıkışmasını ve yayılma yönü boyunca titreşimi tanımlar. Enine ve boyuna polarizasyonların diferansiyel yayılımı sismolojide önemlidir. ⓘ

Polarizasyon durumu

Elektrik alan salınımı ⓘ

Polarizasyon en iyi, başlangıçta sadece saf polarizasyon durumları ve sadece bazı optik frekansta tutarlı bir sinüzoidal dalga düşünülerek anlaşılır. Yandaki diyagramdaki vektör, tek modlu bir lazer tarafından yayılan elektrik alanının salınımını tanımlayabilir (salınım frekansı tipik olarak 10¹⁵ kat daha hızlı olacaktır). Alan x-y düzleminde, sayfa boyunca salınır ve dalga z yönünde, sayfaya dik olarak yayılır. Aşağıdaki ilk iki diyagram, iki farklı yöndeki doğrusal polarizasyon için tam bir döngü boyunca elektrik alan vektörünü izler; bunların her biri farklı bir polarizasyon durumu (SOP) olarak kabul edilir. 45°'deki doğrusal polarizasyonun, yatay olarak doğrusal polarize bir dalga (en soldaki şekilde olduğu gibi) ile aynı fazda aynı genlikte dikey olarak polarize bir dalganın toplanması olarak da görülebileceğini unutmayın. ⓘ

Dört farklı polarizasyon durumunu ve üç ortogonal projeksiyonu gösteren animasyon. ⓘ

90° faz dışı iki doğrusal polarize bileşenin toplamı olarak dairesel polarize bir dalga ⓘ

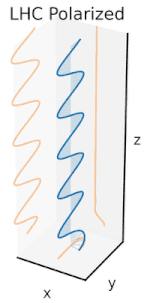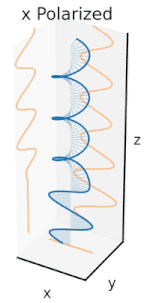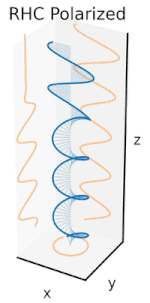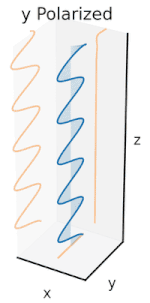
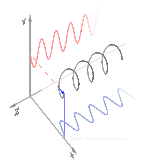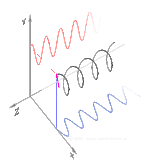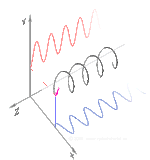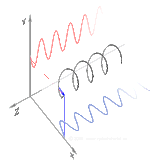
Şimdi bu yatay ve dikey polarizasyon bileşenleri arasına bir faz kayması eklenirse, genellikle üçüncü şekilde gösterildiği gibi eliptik polarizasyon elde edilir. Faz kayması tam olarak ±90° olduğunda, dairesel polarizasyon üretilir (dördüncü ve beşinci şekiller). Uygulamada dairesel polarizasyon, doğrusal polarize ışıkla başlanarak ve böyle bir faz kayması sağlamak için bir çeyrek dalga plakası kullanılarak oluşturulur. Dönen bir elektrik alan vektörüne neden olan bu tür iki faz kaydırmalı bileşenin sonucu sağdaki animasyonda gösterilmektedir. Dairesel veya eliptik polarizasyonun, alanın saat yönünde veya saat yönünün tersine dönmesini içerebileceğini unutmayın. Bunlar, yukarıda gösterilen iki dairesel polarizasyon gibi farklı polarizasyon durumlarına karşılık gelir. ⓘ

Elbette bu tanımda kullanılan x ve y eksenlerinin yönü keyfidir. Böyle bir koordinat sisteminin seçilmesi ve polarizasyon elipsinin x ve y polarizasyon bileşenleri açısından görüntülenmesi, Jones vektörünün (aşağıda) bu temel polarizasyonlar açısından tanımlanmasına karşılık gelir. Tipik olarak, x'in geliş düzleminde olması gibi belirli bir probleme uyacak eksenler seçilir. Geliş düzleminde ve geliş düzlemine dik doğrusal polarizasyonlar için ayrı yansıma katsayıları olduğundan (p ve s polarizasyonları, aşağıya bakınız), bu seçim bir dalganın bir yüzeyden yansımasının hesaplanmasını büyük ölçüde basitleştirir. ⓘ

Dahası, temel fonksiyonlar olarak sadece doğrusal polarizasyonlar değil, herhangi bir ortogonal polarizasyon durumu çifti de kullanılabilir. Örneğin, sağ ve sol dairesel polarizasyonları temel fonksiyonlar olarak seçmek, dairesel çift kırılma (optik aktivite) veya dairesel dikroizm içeren problemlerin çözümünü basitleştirir. ⓘ

Polarizasyon elipsi

Tamamen polarize olmuş monokromatik bir dalga düşünün. Bir salınım döngüsü boyunca elektrik alan vektörü çizilecek olursa, şekilde gösterildiği gibi genellikle eliptik polarizasyonun belirli bir durumuna karşılık gelen bir elips elde edilir. Doğrusal polarizasyon ve dairesel polarizasyonun eliptik polarizasyonun özel durumları olarak görülebileceğini unutmayın. ⓘ

Bir polarizasyon durumu daha sonra elipsin geometrik parametreleri ve "eliptikliği", yani elips etrafındaki dönüşün saat yönünde mi yoksa saat yönünün tersinde mi olduğu ile ilişkili olarak tanımlanabilir. Eliptik şeklin bir parametrelendirmesi, elipsin ana ekseni ile x ekseni arasındaki açı olarak tanımlanan yönelim açısı ψ'yi ve elipsin ana ekseninin küçük eksene oranı olan eliptiklik ε = a/b'yi belirtir. (eksenel oran olarak da bilinir). Eliptiklik parametresi, bir elipsin dış merkezliliğinin alternatif bir parametrelendirmesidir ${\textstyle e={\sqrt {1-b^{2}/a^{2}}},}$ veya eliptiklik açısı, ${\textstyle \chi =\arctan b/a}$ ${\textstyle =\arctan 1/\varepsilon }$ şekilde gösterildiği gibi. χ açısı, Poincaré küresinde (aşağıya bakınız) temsil edildiği gibi polarizasyon durumunun enleminin (ekvatordan açı) ±2χ'ye eşit olması açısından da önemlidir. Doğrusal ve dairesel polarizasyonun özel durumları sırasıyla sonsuzluk ve birlik (veya χ sıfır ve 45°) eliptiklik ε'ye karşılık gelir. ⓘ

Jones vektörü

Tamamen polarize bir durum hakkında tam bilgi, polarizasyon düzlemindeki elektrik alan vektörünün iki bileşenindeki salınımların genliği ve fazı ile de sağlanır. Bu gösterim yukarıda farklı polarizasyon durumlarının nasıl mümkün olduğunu göstermek için kullanılmıştır. Genlik ve faz bilgisi, iki boyutlu karmaşık bir vektör (Jones vektörü) olarak uygun bir şekilde temsil edilebilir:

$\mathbf {e} ={\begin{bmatrix}a_{1}e^{i\theta _{1}}\\a_{2}e^{i\theta _{2}}\end{bmatrix}}.$ ⓘ

Burada $a_{1}$ ve $a_{2}$ elektrik alan vektörünün iki bileşenindeki dalganın genliğini gösterirken $\theta _{1}$ ve $\theta _{2}$ fazları temsil eder. Bir Jones vektörünün birim modüllü karmaşık bir sayı ile çarpımı, aynı elipsi ve dolayısıyla aynı kutuplaşma durumunu temsil eden farklı bir Jones vektörü verir. Jones vektörünün gerçek kısmı olan fiziksel elektrik alanı değişecektir ancak polarizasyon durumunun kendisi mutlak fazdan bağımsızdır. Jones vektörünü temsil etmek için kullanılan temel vektörlerin doğrusal polarizasyon durumlarını temsil etmesi (yani gerçek olması) gerekmez. Genel olarak herhangi iki ortogonal durum kullanılabilir, burada bir ortogonal vektör çifti resmi olarak sıfır iç çarpıma sahip olan olarak tanımlanır. Yaygın bir seçim sol ve sağ dairesel polarizasyonlardır, örneğin dairesel çift kırılımlı ortamda (aşağıya bakınız) bu tür iki bileşendeki dalgaların farklı yayılımını veya dairesel polarizasyona duyarlı tutarlı dedektörlerin sinyal yollarını modellemek için. ⓘ

Koordinat çerçevesi

Polarizasyon durumunun geometrik parametreler veya Jones vektörleri kullanılarak temsil edilip edilmediğine bakılmaksızın, parametrelendirmede koordinat çerçevesinin yönü örtüktür. Bu, yayılma yönü etrafında dönme gibi bir serbestlik derecesine izin verir. Dünya yüzeyine paralel olarak yayılan ışık düşünüldüğünde, "yatay" ve "dikey" polarizasyon terimleri sıklıkla kullanılır; bunlardan ilki Jones vektörünün ilk bileşeni veya sıfır azimut açısı ile ilişkilendirilir. Öte yandan, astronomide bunun yerine genellikle ekvatoral koordinat sistemi kullanılır ve sıfır azimut (veya yatay koordinat sistemiyle karıştırılmaması için astronomide daha yaygın olarak adlandırıldığı şekliyle konum açısı) tam kuzeye karşılık gelir. ⓘ

s ve p tanımlamaları

Elektromanyetik vektörler için ${\textstyle {\textbf {E}}}$, ${\textstyle {\textbf {B}}}$ ve ${\textstyle {\textbf {k}}}$ ile ${\textstyle {\textbf {E}}={\textbf {E}}(x,y)}$ 3 düzlemsel projeksiyon ve toplam elektrik alanının deformasyon yüzeyi ile birlikte. Işık xy düzleminde daima s-polarizedir. ${\textstyle \theta }$ kutup açısıdır. ${\textstyle {\textbf {k}}}$ ve ${\textstyle \varphi _{E}}$ 'nin azimut açısıdır. ${\textstyle {\textbf {E}}}$. ⓘ

Sıklıkla kullanılan bir başka koordinat sistemi de geliş düzlemiyle ilgilidir. Bu, gelen yayılma yönü ve bir arayüzey düzlemine dik vektör tarafından yapılan düzlemdir, başka bir deyişle, ışının yansıma veya kırılmadan önce ve sonra hareket ettiği düzlemdir. Elektrik alanının bu düzleme paralel olan bileşeni p-like (paralel), bu düzleme dik olan bileşeni ise s-like (senkrecht, Almanca dik anlamına gelir) olarak adlandırılır. Elektrik alanı geliş düzlemi boyunca olan polarize ışık bu nedenle p-polarize olarak adlandırılırken, elektrik alanı geliş düzlemine normal olan ışık s-polarize olarak adlandırılır. P polarizasyonu genellikle enine manyetik (TM) olarak adlandırılır ve pi-polarize veya teğetsel düzlem polarizasyonu olarak da adlandırılır. S polarizasyonu ayrıca enine-elektrik (TE) olarak adlandırılır ve sigma-polarize veya sagital düzlem polarize olarak da adlandırılır. ⓘ

Polarize edilmemiş ve kısmen polarize edilmiş ışık

Tanım

Doğal ışık, diğer yaygın görünür ışık kaynakları gibi tutarsızdır: radyasyon, emisyonları birbiriyle ilişkili olmayan ve genellikle rastgele polarizasyonlara sahip olan çok sayıda atom veya molekül tarafından bağımsız olarak üretilir. Bu durumda ışığın polarize olmadığı söylenir. Bu terim biraz kesin değildir, çünkü herhangi bir zaman anında bir konumda elektrik ve manyetik alanların belirli bir yönü vardır, ancak kutuplaşmanın zaman içinde o kadar hızlı değiştiğini ima eder ki ölçülmez veya bir deneyin sonucuyla ilgili olmaz. Depolarize edici olarak adlandırılan bir ışın, polarize edilmiş bir ışın üzerinde etki ederek aslında her noktada tamamen polarize edilmiş, ancak polarizasyonun ışın boyunca o kadar hızlı değiştiği bir ışın oluşturur ki, amaçlanan uygulamalarda göz ardı edilebilir. ⓘ

Polarize olmayan ışık, her biri yarı yoğunlukta olan iki bağımsız zıt polarize akımın karışımı olarak tanımlanabilir. Bu akımlardan birinde diğerinden daha fazla güç olduğunda ışığın kısmen polarize olduğu söylenir. Herhangi bir dalga boyunda, kısmen polarize olmuş ışık istatistiksel olarak tamamen polarize olmamış bir bileşen ile tamamen polarize olmuş bir bileşenin süperpozisyonu olarak tanımlanabilir. Bu durumda ışık, polarizasyon derecesi ve polarize bileşenin parametreleri açısından tanımlanabilir. Bu polarize bileşen, yukarıda ayrıntılı olarak açıklandığı gibi bir Jones vektörü veya polarizasyon elipsi cinsinden tanımlanabilir. Bununla birlikte, polarizasyon derecesini de tanımlamak için, normalde kısmi polarizasyon durumunu belirtmek için Stokes parametreleri (aşağıya bakınız) kullanılır. ⓘ

Motivasyon

Düzlem dalgaların homojen bir ortamdan geçişi Jones vektörleri ve 2×2 Jones matrisleri cinsinden tam olarak tanımlanır. Ancak pratikte, uzaysal homojensizlik veya karşılıklı tutarsız dalgaların varlığı nedeniyle ışığın tamamının bu kadar basit bir şekilde görülemediği durumlar vardır. Örneğin depolarizasyon olarak adlandırılan durum Jones matrisleri kullanılarak tanımlanamaz. Bu durumlar için Stokes 4-vektörü üzerinde etkili olan 4×4 matrisinin kullanılması olağandır. Bu tür matrisler ilk olarak 1929 yılında Paul Soleillet tarafından kullanılmış, ancak daha sonra Mueller matrisleri olarak bilinmeye başlanmıştır. Her Jones matrisi bir Mueller matrisine sahipken, bunun tersi doğru değildir. Mueller matrisleri daha sonra, şimdi sunulacağı gibi, dalgaların karmaşık yüzeylerden veya parçacık topluluklarından saçılmasının gözlemlenen polarizasyon etkilerini tanımlamak için kullanılır. ⓘ

Tutarlılık matrisi

Jones vektörü, yukarıda açıklandığı gibi saf bir polarizasyon durumunu temsil eden tek bir monokromatik dalganın polarizasyon ve faz durumunu mükemmel bir şekilde tanımlar. Ancak farklı polarizasyonlara (hatta farklı frekanslara) sahip dalgaların herhangi bir karışımı bir Jones vektörüne karşılık gelmez. Kısmen polarize radyasyon olarak adlandırılan durumda alanlar stokastiktir ve elektrik alanının bileşenleri arasındaki değişimler ve korelasyonlar sadece istatistiksel olarak tanımlanabilir. Böyle bir gösterim tutarlılık matrisidir:

${\begin{aligned}\mathbf {\Psi } &=\left\langle \mathbf {e} \mathbf {e} ^{\dagger }\right\rangle \\&=\left\langle {\begin{bmatrix}e_{1}e_{1}^{*}&e_{1}e_{2}^{*}\\e_{2}e_{1}^{*}&e_{2}e_{2}^{*}\end{bmatrix}}\right\rangle \\&=\left\langle {\begin{bmatrix}a_{1}^{2}&a_{1}a_{2}e^{i\left(\theta _{1}-\theta _{2}\right)}\\a_{1}a_{2}e^{-i\left(\theta _{1}-\theta _{2}\right)}&a_{2}^{2}\end{bmatrix}}\right\rangle \end{aligned}}$ ⓘ

Burada açısal parantezler birçok dalga döngüsünün ortalamasını gösterir. Tutarlılık matrisinin çeşitli varyantları önerilmiştir: Wiener tutarlılık matrisi ve Richard Barakat'ın spektral tutarlılık matrisi sinyalin spektral ayrışımının tutarlılığını ölçerken, Wolf tutarlılık matrisi tüm zaman/frekansların ortalamasını alır. ⓘ

Tutarlılık matrisi, polarizasyonla ilgili tüm ikinci dereceden istatistiksel bilgileri içerir. Bu matris, tutarlılık matrisinin öz vektörlerine karşılık gelen ve her biri diğerine ortogonal olan bir polarizasyon durumunu temsil eden iki idempotent matrisin toplamına ayrıştırılabilir. Alternatif bir ayrıştırma ise tamamen polarize (sıfır determinant) ve polarize olmayan (ölçeklendirilmiş özdeşlik matrisi) bileşenlerdir. Her iki durumda da, bileşenlerin toplanması işlemi, iki bileşenden gelen dalgaların tutarsız süperpozisyonuna karşılık gelir. İkinci durum "polarizasyon derecesi" kavramını ortaya çıkarır; yani, toplam yoğunluğun tamamen polarize bileşen tarafından katkıda bulunulan kısmı. ⓘ

Stokes parametreleri

Tutarlılık matrisini görselleştirmek kolay değildir ve bu nedenle tutarsız veya kısmen polarize radyasyonu toplam yoğunluğu (I), (kesirli) polarizasyon derecesi (p) ve polarizasyon elipsinin şekil parametreleri açısından tanımlamak yaygındır. Alternatif ve matematiksel olarak uygun bir tanım, 1852 yılında George Gabriel Stokes tarafından tanıtılan Stokes parametreleri ile verilir. Stokes parametrelerinin yoğunluk ve polarizasyon elipsi parametreleriyle ilişkisi aşağıdaki denklemlerde ve şekilde gösterilmiştir. ⓘ

$S_{0}=I\,$

$S_{1}=Ip\cos 2\psi \cos 2\chi \,$

$S_{2}=Ip\sin 2\psi \cos 2\chi \,$

$S_{3}=Ip\sin 2\chi \,$ ⓘ

Burada Ip, 2ψ ve 2χ, son üç Stokes parametresinin üç boyutlu uzayında polarizasyon durumunun küresel koordinatlarıdır. Herhangi bir polarizasyon elipsinin 180° döndürülmüş veya yarı eksen uzunlukları 90° döndürme ile birlikte değiştirilmiş bir elipsten ayırt edilemeyeceği gerçeğine karşılık gelen ψ ve χ'den önceki iki faktörüne dikkat edin. Stokes parametreleri bazen I, Q, U ve V olarak gösterilir. ⓘ

Dört Stokes parametresi, paraksiyel bir dalganın 2D polarizasyonunu tanımlamak için yeterlidir, ancak genel bir paraksiyel olmayan dalganın veya bir evanescent alanın 3D polarizasyonunu tanımlamak için yeterli değildir. ⓘ

Poincaré küresi

İlk Stokes parametresi S₀ (veya I) ihmal edildiğinde, diğer üç Stokes parametresi doğrudan üç boyutlu Kartezyen koordinatlarda çizilebilir. Polarize bileşende verilen bir güç için

$P={\sqrt {S_{1}^{2}+S_{2}^{2}+S_{3}^{2}}}$ ⓘ

Tüm kutuplaşma durumları kümesi daha sonra, ekteki diyagramda gösterildiği gibi, Poincaré küresinin (ancak P yarıçaplı) yüzeyindeki noktalarla eşleştirilir. ⓘ

Üzerinde veya altında üç Stokes parametresinin [S₁, S₂, S₃] (veya [Q, U, V]) Kartezyen koordinatlarda çizildiği Poincaré küresi ⓘ

Kutuplaşma durumlarının Poincaré küresi üzerinde gösterimi ⓘ

Genellikle toplam ışın gücü ilgi çekici değildir, bu durumda Stokes vektörü toplam S₀ yoğunluğuna bölünerek normalleştirilmiş bir Stokes vektörü kullanılır:

$\mathbf {S'} ={\frac {1}{S_{0}}}{\begin{bmatrix}S_{0}\\S_{1}\\S_{2}\\S_{3}\end{bmatrix}}.$ ⓘ

Normalleştirilmiş Stokes vektörü $\mathbf {S'}$ o zaman birlik gücüne sahiptir ($S'_{0}=1$) ve üç boyutta çizilen üç önemli Stokes parametresi, saf polarizasyon durumları için tek yarıçaplı Poincaré küresi üzerinde yer alacaktır (burada $P'_{0}=1$). Kısmen polarize olmuş durumlar Poincaré küresinin içinde şu mesafede yer alacaktır $P'={\sqrt {S_{1}'^{2}+S_{2}'^{2}+S_{3}'^{2}}}$ orijinden. Polarize olmayan bileşen ilgi çekici olmadığında, Stokes vektörü elde etmek için daha da normalleştirilebilir

$\mathbf {S} ={\frac {1}{P'}}{\begin{bmatrix}1\\S'_{1}\\S'_{2}\\S'_{3}\end{bmatrix}}={\frac {1}{P}}{\begin{bmatrix}S_{0}\\S_{1}\\S_{2}\\S_{3}\end{bmatrix}}.$ ⓘ

Çizildiğinde, bu nokta tek yarıçaplı Poincaré küresinin yüzeyinde yer alacak ve polarize bileşenin polarizasyon durumunu gösterecektir. ⓘ

Poincaré küresi üzerindeki herhangi iki antipodal nokta ortogonal polarizasyon durumlarını ifade eder. Herhangi iki polarizasyon durumu arasındaki örtüşme yalnızca küre üzerindeki konumları arasındaki mesafeye bağlıdır. Sadece saf polarizasyon durumları bir küre üzerine eşlendiğinde doğru olabilen bu özellik, Poincaré küresinin icadı ve Stokes parametrelerinin kullanımı için motivasyondur, bu nedenle üzerinde (veya altında) çizilir. ⓘ

IEEE'nin RHCP ve LHCP'yi Fizikçiler tarafından kullanılanların tam tersi olarak tanımladığını unutmayın. IEEE 1979 Anten Standardı RHCP'yi Poincare Küresinin Güney Kutbunda gösterecektir. IEEE RHCP'yi başparmak iletim yönünü gösterirken sağ eli kullanarak ve parmaklar E alanının zamanla dönüş yönünü göstererek tanımlar. Fizikçiler ve Mühendisler tarafından kullanılan zıt konvansiyonların mantığı, Astronomik Gözlemlerin her zaman gelen dalga gözlemciye doğru ilerlerken yapılmasıdır, oysa çoğu mühendis için vericinin arkasında durdukları ve kendilerinden uzaklaşan dalgayı izledikleri varsayılır. Bu makale IEEE 1979 Anten Standardını kullanmamaktadır ve IEEE çalışmalarında tipik olarak kullanılan +t kuralını kullanmamaktadır. ⓘ

Yansıma ve yayılma için çıkarımlar

Dalga yayılımında polarizasyon

Vakumda, elektrik alanının bileşenleri ışık hızında yayılır, böylece dalganın fazı uzay ve zamanda değişirken polarizasyon durumu değişmez. Yani, +z yönündeki bir düzlem dalganın elektrik alan vektörü e aşağıdaki gibidir:

$\mathbf {e} (z+\Delta z,t+\Delta t)=\mathbf {e} (z,t)e^{ik(c\Delta t-\Delta z)},$ ⓘ

burada k dalga sayısıdır. Yukarıda belirtildiği gibi, anlık elektrik alanı Jones vektörü ile faz faktörünün çarpımının gerçek kısmıdır $e^{-i\omega t}$. Bir elektromanyetik dalga madde ile etkileşime girdiğinde, yayılımı malzemenin (karmaşık) kırılma indisine göre değişir. Bu kırılma indisinin gerçek veya hayali kısmı bir dalganın polarizasyon durumuna bağlı olduğunda, sırasıyla çift kırılma ve polarizasyon dikroizmi (veya diattenuation) olarak bilinen özellikler, o zaman bir dalganın polarizasyon durumu genellikle değişecektir. ⓘ

Bu tür ortamlarda, herhangi bir polarizasyon durumuna sahip bir elektromanyetik dalga, farklı yayılma sabitleriyle karşılaşan iki ortogonal polarize bileşene ayrıştırılabilir. Belirli bir yol üzerindeki yayılmanın bu iki bileşen üzerindeki etkisi, Jones matrisi olarak bilinen karmaşık bir 2×2 dönüşüm matrisi J biçiminde en kolay şekilde karakterize edilir:

$\mathbf {e'} =\mathbf {J} \mathbf {e} .$ ⓘ

Saydam bir malzemeden geçişten kaynaklanan Jones matrisi, yayılma mesafesinin yanı sıra çift kırılmaya da bağlıdır. Çift kırılma (ortalama kırılma indisinin yanı sıra) genellikle dağıtıcı olacaktır, yani optik frekansın (dalga boyu) bir fonksiyonu olarak değişecektir. Bununla birlikte, çift kırılmayan malzemeler söz konusu olduğunda, 2×2 Jones matrisi kimlik matrisidir (skaler bir faz faktörü ve zayıflama faktörü ile çarpılır), bu da yayılma sırasında polarizasyonda herhangi bir değişiklik olmadığını gösterir. ⓘ

İki ortogonal modda yayılma etkileri için Jones matrisi şu şekilde yazılabilir ⓘ

$\mathbf {J} =\mathbf {T} {\begin{bmatrix}g_{1}&0\\0&g_{2}\end{bmatrix}}\mathbf {T} ^{-1},$ ⓘ

burada g₁ ve g₂ karmaşık sayılardır faz gecikmesini ve muhtemelen iki polarizasyon özmodunun her birinde yayılmaya bağlı genlik zayıflamasını tanımlar. T, bu yayılma modlarından Jones vektörleri için kullanılan doğrusal sisteme bir temel değişikliğini temsil eden üniter bir matristir; doğrusal çift kırılma veya diattenuation durumunda modların kendileri doğrusal polarizasyon durumlarıdır, bu nedenle koordinat eksenleri uygun şekilde seçilmişse T ve T-1 ihmal edilebilir. ⓘ

Çift kırılma

Çift kırılgan olarak adlandırılan, genliklerin değişmediği ancak diferansiyel bir faz gecikmesinin meydana geldiği ortamlarda Jones matrisi üniter bir matristir: |g₁| = g₂| = 1. Sadece iki polarizasyonun genliklerinin farklı şekilde etkilendiği diattenuating (veya polarizasyon anlamında dikroik) olarak adlandırılan ortam, bir Hermitian matris (genellikle ortak bir faz faktörü ile çarpılır) kullanılarak tanımlanabilir. Aslında, herhangi bir matris üniter ve pozitif Hermitian matrislerin çarpımı olarak yazılabileceğinden, polarizasyona bağlı optik bileşenlerin herhangi bir dizisi boyunca ışık yayılımı, bu iki temel dönüşüm türünün çarpımı olarak yazılabilir. ⓘ

İki çapraz polarizör arasına yerleştirildiğinde stres kaynaklı çift kırılma gösteren plastik bir kutunun renk deseni. ⓘ

Çift kırılmalı ortamda zayıflama yoktur, ancak iki mod diferansiyel faz gecikmesi tahakkuk ettirir. Doğrusal çift kırılmanın iyi bilinen tezahürleri (yani, temel polarizasyonların ortogonal doğrusal polarizasyonlar olduğu) optik dalga plakalarında / geciktiricilerde ve birçok kristalde görülür. Doğrusal olarak polarize olmuş ışık çift kırılgan bir malzemeden geçerse, polarizasyon yönü bu temel polarizasyonlardan biriyle aynı değilse, polarizasyon durumu genellikle değişecektir. Faz kayması ve dolayısıyla polarizasyon durumundaki değişim genellikle dalga boyuna bağlı olduğundan, iki polarizör arasında beyaz ışık altında görüntülenen bu tür nesneler, ekteki fotoğrafta görüldüğü gibi renkli etkilere yol açabilir. ⓘ

Dairesel çift kırılma, özellikle kiral sıvılarda optik aktivite veya yayılma yönü boyunca bir manyetik alanın varlığına bağlı olarak Faraday rotasyonu olarak da adlandırılır. Doğrusal olarak kutuplanmış ışık böyle bir nesneden geçirildiğinde, hala doğrusal olarak kutuplanmış, ancak kutuplaşma ekseni döndürülmüş olarak çıkacaktır. Doğrusal ve dairesel çift kırılmanın bir kombinasyonu, temel polarizasyonlar olarak iki ortogonal eliptik polarizasyona sahip olacaktır; ancak "eliptik çift kırılma" terimi nadiren kullanılır. ⓘ

Çift kırılma altında Poincaré küresinde vektörler tarafından alınan yollar. Yayılma modları (dönme eksenleri) kırmızı, mavi ve sarı çizgilerle, başlangıç vektörleri kalın siyah çizgilerle ve aldıkları yollar renkli elipslerle (üç boyutta daireleri temsil eder) gösterilmiştir. ⓘ

Doğrusal çift kırılma durumu (iki ortogonal doğrusal yayılma modu ile), bu modlara 45° açıyla doğrusal olarak kutuplanmış gelen bir dalga ile görselleştirilebilir. Bir diferansiyel faz tahakkuk etmeye başladığında, polarizasyon eliptik hale gelir, sonunda tamamen dairesel polarizasyona (90° faz farkı), sonra eliptik ve sonunda orijinal polarizasyona dik doğrusal polarizasyona (180° faz), sonra tekrar dairesel (270° faz), sonra orijinal azimut açısı ile eliptik ve son olarak döngünün yeniden başladığı orijinal doğrusal polarize duruma (360° faz) geri döner. Genel olarak durum daha karmaşıktır ve yayılma modları tarafından tanımlanan eksen etrafında Poincaré küresinde bir dönüş olarak karakterize edilebilir. Doğrusal (mavi), dairesel (kırmızı) ve eliptik (sarı) çift kırılma örnekleri soldaki şekilde gösterilmiştir. Toplam yoğunluk ve polarizasyon derecesi etkilenmez. Çift kırılgan ortamdaki yol uzunluğu yeterliyse, son yayılma yönleri aynı olsa bile (giriş yüzü ve çıkış yüzünün paralel olduğu varsayılırsa) kolimasyonlu bir ışının (veya ışının) iki polarizasyon bileşeni malzemeden konumsal bir kayma ile çıkabilir. Bu durum genellikle, izleyiciye kristalin arkasındaki bir nesnenin zıt polarizasyonlarda hafifçe kaymış iki görüntüsünü sunan kalsit kristalleri kullanılarak görülür. Bu etki, 1669 yılında Erasmus Bartholinus tarafından polarizasyonun ilk keşfini sağlamıştır. ⓘ

Dikroizm

Bir polarizasyon modunun iletiminin tercihli olarak azaltıldığı ortamlara dikroik veya diattenüasyon denir. Çift kırılma gibi, diattenüasyon da doğrusal polarizasyon modlarına (bir kristalde) veya dairesel polarizasyon modlarına (genellikle bir sıvıda) göre olabilir. ⓘ

Bir moddaki radyasyonun neredeyse tamamını bloke eden cihazlar polarize filtreler veya basitçe "polarizörler" olarak bilinir. Bu, Jones matrisinin yukarıdaki gösteriminde g₂=0'a karşılık gelir. İdeal bir polarizörün çıkışı, giriş dalgasının o polarizasyon modundaki orijinal genliğine eşit bir genliğe sahip belirli bir polarizasyon durumudur (genellikle doğrusal polarizasyon). Diğer polarizasyon modundaki güç ortadan kaldırılır. Böylece polarize edilmemiş ışık ideal bir polarizörden geçirilirse (g₁=1 ve g₂=0) başlangıçtaki gücünün tam olarak yarısı korunur. Pratik polarizörler, özellikle ucuz tabaka polarizörler, ek kayıplara sahiptir, böylece g₁ < 1. Ancak, birçok durumda daha önemli olan değer, polarizörün polarizasyon derecesi veya sönme oranıdır; bunlar g₁ ile g₂'nin karşılaştırılmasını içerir. Jones vektörleri dalgaların genliklerini (yoğunluktan ziyade) ifade ettiğinden, polarize edilmemiş ışıkla aydınlatıldığında istenmeyen polarizasyonda kalan güç, amaçlanan polarizasyondaki gücün (g₂/g₁)²'si olacaktır. ⓘ

Speküler yansıma

Genişletilmiş ortamdaki çift kırılma ve dikroizme ek olarak, Jones matrisleri kullanılarak tanımlanabilen polarizasyon etkileri, farklı kırılma indisine sahip iki malzeme arasındaki (yansıtıcı) arayüzde de meydana gelebilir. Bu etkiler Fresnel denklemleri ile ele alınır. Dalganın bir kısmı iletilir ve bir kısmı yansıtılır; belirli bir malzeme için bu oranlar (ve ayrıca yansıma fazı) geliş açısına bağlıdır ve s ve p polarizasyonları için farklıdır. Bu nedenle, yansıyan ışığın polarizasyon durumu (başlangıçta polarize olmamış olsa bile) genellikle değişir. ⓘ

Bir ışına Brewster açısındaki bir plaka yığını, her yüzeydeki s-polarize ışığın bir kısmını yansıtır ve (bu tür birçok plakadan sonra) esas olarak p-polarize bir ışın bırakır. ⓘ

Brewster açısı olarak bilinen ve p polarizasyonu için yansıma katsayısının sıfır olduğu özel bir geliş açısında bir yüzeye çarpan herhangi bir ışık, sadece s-polarizasyonu kalacak şekilde yansıtılacaktır. Bu prensip, s polarizasyonunun bir kısmının her Brewster açılı yüzeyde yansıma yoluyla uzaklaştırıldığı ve bu tür birçok yüzeyden geçtikten sonra geriye sadece p polarizasyonunun kaldığı "plakalar yığını polarizöründe" (şekle bakın) kullanılır. P polarizasyonunun genellikle daha küçük olan yansıma katsayısı, polarize güneş gözlüklerinin de temelini oluşturur; s (yatay) polarizasyonunu bloke ederek, örneğin ıslak bir caddeden yansıma nedeniyle oluşan parlamanın çoğu ortadan kaldırılır. ⓘ

Normal gelişte yansımanın önemli özel durumunda (anizotropik malzemeleri içermeyen) belirli bir s veya p polarizasyonu yoktur. Hem x hem de y polarizasyon bileşenleri aynı şekilde yansıtılır ve bu nedenle yansıyan dalganın polarizasyonu gelen dalganınkiyle aynıdır. Bununla birlikte, dairesel (veya eliptik) polarizasyon durumunda, polarizasyon durumunun yönü tersine çevrilir, çünkü geleneksel olarak bu, yayılma yönüne göre belirtilir. Elektrik alanının x-y eksenleri etrafındaki dairesel dönüşü, +z yönündeki bir dalga için "sağ-elli" olarak adlandırılırken, -z yönündeki bir dalga için "sol-elli "dir. Ancak sıfır olmayan bir geliş açısındaki genel yansıma durumunda böyle bir genelleme yapılamaz. Örneğin, bir dielektrik yüzeyden otlatma açısıyla yansıyan sağ-dairesel polarize ışık, yine de sağ-elli (ancak eliptik olarak) polarize olacaktır. Bir metalden normal olmayan bir açıyla yansıyan doğrusal polarize ışık genellikle eliptik olarak polarize olur. Bu durumlar, s ve p polarizasyon bileşenleri için farklı Fresnel katsayılarının etki ettiği Jones vektörleri kullanılarak ele alınır. ⓘ

Polarizasyon içeren ölçüm teknikleri

Bazı optik ölçüm teknikleri polarizasyona dayanır. Diğer birçok optik teknikte polarizasyon çok önemlidir veya en azından dikkate alınmalı ve kontrol edilmelidir; bu tür örnekler sayılamayacak kadar çoktur. ⓘ

Stres ölçümü

Plastik camlarda stres ⓘ

Mühendislikte, stres kaynaklı çift kırılma olgusu şeffaf malzemelerdeki streslerin kolayca gözlemlenmesini sağlar. Yukarıda belirtildiği ve ekteki fotoğrafta görüldüğü gibi, çift kırılmanın kromatikliği, iki polarizör arasında bakıldığında tipik olarak renkli desenler oluşturur. Dış kuvvetler uygulandıkça, malzemede indüklenen iç gerilim böylece gözlemlenir. Buna ek olarak, çift kırılma sıklıkla üretim sırasında "dondurulmuş" gerilimler nedeniyle gözlemlenir. Bu, çift kırılmanın üretim sürecinde malzemenin gerilmesinden kaynaklandığı selofan bantta ünlü bir şekilde gözlemlenir. ⓘ

Elipsometri

Elipsometri, düzgün bir yüzeyin optik özelliklerinin ölçümü için güçlü bir tekniktir. Böyle bir yüzeyden speküler yansımayı takiben ışığın polarizasyon durumunun ölçülmesini içerir. Bu tipik olarak geliş açısı veya dalga boyunun (veya her ikisinin) bir fonksiyonu olarak yapılır. Elipsometri yansımaya dayandığından, numunenin ışığa karşı şeffaf olması veya arka tarafının erişilebilir olması gerekmez. ⓘ

Elipsometri, bir yığın malzemenin bir yüzeyinin (karmaşık) kırılma indisini modellemek için kullanılabilir. Ayrıca bir alt tabaka üzerinde biriken bir veya daha fazla ince film tabakasının parametrelerinin belirlenmesinde de çok kullanışlıdır. Yansıma özellikleri nedeniyle, sadece p ve s polarizasyon bileşenlerinin tahmin edilen büyüklüğü değil, aynı zamanda yansıma üzerine göreceli faz kaymaları da bir elipsometre kullanılarak yapılan ölçümlerle karşılaştırılır. Normal bir elipsometre gerçek yansıma katsayısını değil (aydınlatıcı ışının dikkatli bir şekilde fotometrik kalibrasyonunu gerektirir), p ve s yansımalarının oranını ve incelenen yüzey tarafından yansıma üzerine indüklenen polarizasyon eliptikliğinin (dolayısıyla adı) değişimini ölçer. Elipsometreler, bilim ve araştırmada kullanılmalarının yanı sıra, örneğin üretim süreçlerini kontrol etmek için yerinde de kullanılırlar. ⓘ

Jeoloji

Bir volkanik kum tanesinin fotomikrografı; üstteki resim düzlem polarize ışık, alttaki resim çapraz polarize ışık, sol merkezdeki ölçek kutusu 0,25 milimetredir. ⓘ

(Doğrusal) çift kırılma özelliği kristal minerallerde yaygındır ve aslında polarizasyonun ilk keşfinde çok önemli bir rol oynamıştır. Mineralojide, mineralleri tanımlamak amacıyla polarizasyon mikroskopları kullanılarak bu özellikten sıklıkla yararlanılır. Daha fazla ayrıntı için optik mineralojiye bakınız. ⓘ

Katı malzemelerdeki ses dalgaları polarizasyon sergiler. Üç kutuplaşmanın yeryüzünde farklı şekilde yayılması sismoloji alanında çok önemlidir. Yatay ve dikey polarizasyonlu sismik dalgalar (kesme dalgaları) SH ve SV olarak adlandırılırken, uzunlamasına polarizasyonlu dalgalar (sıkıştırma dalgaları) P dalgaları olarak adlandırılır. ⓘ

Kimya

Yukarıda bir kristal türünün çift kırılmasının onu tanımlamada faydalı olduğunu gördük ve bu nedenle doğrusal çift kırılmanın tespiti özellikle jeoloji ve mineralojide faydalıdır. Doğrusal polarize ışık genellikle böyle bir kristalden geçerken polarizasyon durumu değişir ve yukarıdaki fotoğrafta görüldüğü gibi iki çapraz polarizör arasında görüntülendiğinde öne çıkar. Benzer şekilde, kimyada, sıvı bir çözeltide polarizasyon eksenlerinin dönmesi yararlı bir ölçüm olabilir. Bir sıvıda doğrusal çift kırılma mümkün değildir, ancak kiral bir molekül çözelti içindeyken dairesel çift kırılma olabilir. Böyle bir molekülün sağ ve sol elli enantiyomerleri eşit sayıda bulunduğunda (rasemik karışım olarak adlandırılır) etkileri iptal olur. Bununla birlikte, organik moleküllerde daha sık görüldüğü gibi, sadece bir tane (veya birinin üstünlüğü) olduğunda, bu dengesizliğin büyüklüğünü (veya sadece bir enantiyomerin mevcut olduğu varsayıldığında molekülün konsantrasyonunu) ortaya çıkaran net bir dairesel çift kırılma (veya optik aktivite) gözlemlenir. Bu, polarize ışığın sıvının bir tüpünden geçirildiği bir polarimetre kullanılarak ölçülür, bunun sonunda ışığın içinden geçişini geçersiz kılmak için döndürülen başka bir polarizör bulunur. ⓘ

Astronomi

Astronominin birçok alanında, dış uzaydan gelen polarize elektromanyetik radyasyonun incelenmesi büyük önem taşımaktadır. Genellikle yıldızların termal radyasyonunda bir faktör olmamasına rağmen, polarizasyon aynı zamanda tutarlı astronomik kaynaklardan (örneğin hidroksil veya metanol maserleri) ve aktif galaksilerdeki büyük radyo lobları ve pulsar radyo radyasyonu (bazen tutarlı olabileceği tahmin edilmektedir) gibi tutarsız kaynaklardan gelen radyasyonda da mevcuttur ve yıldızlararası tozdan saçılma yoluyla yıldız ışığına da uygulanır. Kutuplaşma, radyasyon ve saçılma kaynakları hakkında bilgi sağlamanın yanı sıra, Faraday dönüşü yoluyla yıldızlararası manyetik alanı da araştırır. Kozmik mikrodalga arka planının polarizasyonu, çok erken evrenin fiziğini incelemek için kullanılmaktadır. Sinkrotron radyasyonu doğası gereği polarizedir. Astronomik kaynakların Dünya'daki biyolojik moleküllerin kiralitesine neden olduğu öne sürülmüştür. ⓘ

Uygulamalar ve örnekler

Polarize güneş gözlüğü

Polarizörün çamur düzlüklerinden yansıma üzerindeki etkisi. Soldaki resimde, yatay olarak yönlendirilmiş polarizör tercihen bu yansımaları iletir; polarize güneş gözlüğü kullanarak görüntüleyeceğiniz gibi polarizörü 90 ° döndürmek (sağda) neredeyse tüm speküler olarak yansıyan güneş ışığını engeller. ⓘ

Güneş gözlüklerinin polarize olup olmadığı, biri diğerine dik olacak şekilde iki çift gözlüğe bakılarak test edilebilir. Eğer her ikisi de polarize ise, tüm ışık engellenecektir. ⓘ

Polarize olmayan ışık, speküler (parlak) bir yüzey tarafından yansıtıldıktan sonra genellikle bir derece polarizasyon elde eder. Bu olgu 1808 yılında matematikçi Étienne-Louis Malus tarafından gözlemlenmiş ve Malus yasasına bu isim verilmiştir. Polarize güneş gözlükleri bu etkiden yararlanarak yatay yüzeylerin, özellikle de otlatma açısıyla bakıldığında öndeki yolun yansımalarından kaynaklanan parlamayı azaltır. ⓘ

Polarize güneş gözlüğü kullananlar, yansıma veya saçılma yoluyla doğal polarizasyonla birlikte, örneğin sertleştirilmiş camlarda (örneğin araba camları) veya şeffaf plastikten yapılmış eşyalarda renge bağlı çift kırılma etkileri gibi kasıtsız polarizasyon etkilerini zaman zaman gözlemleyecektir. LCD monitörlerden gelen polarize ışık (aşağıya bakınız), bunlar takıldığında çok dikkat çekicidir. ⓘ

Gökyüzü polarizasyonu ve fotoğrafçılık

Polarize filtrenin (sağdaki resim) bir fotoğrafta gökyüzü üzerindeki etkileri ⓘ

Polarizasyon, Dünya atmosferinden geçerken aerosoller tarafından saçılan güneş ışığından kaynaklandığı için gökyüzünün ışığında gözlemlenir. Saçılan ışık, açık gökyüzündeki parlaklığı ve rengi üretir. Saçılan ışığın bu kısmi polarizasyonu, fotoğraflarda gökyüzünü koyulaştırmak ve kontrastı artırmak için kullanılabilir. Bu etki en güçlü şekilde gökyüzünde Güneş'e 90° açı yapan noktalarda gözlemlenir. Polarize filtreler bu etkileri, gökyüzünden yansıma veya saçılmanın söz konusu olduğu sahnelerin fotoğraflanmasında sonuçları optimize etmek için kullanır. ⓘ

Embassy Gardens Gökyüzü Havuzu'na polarizörle bakıldığında, tavan penceresindeki gerilime bağlı çift kırılma nedeniyle oluşan renkli saçaklar ⓘ

Gökyüzü polarizasyonu navigasyonda oryantasyon için kullanılmıştır. Pfund gökyüzü pusulası 1950'lerde Dünya'nın manyetik alanının kutuplarına yakın yerlerde ne güneşin ne de yıldızların görünmediği durumlarda (örneğin gündüz bulut veya alacakaranlık altında) navigasyon yaparken kullanılmıştır. Manyetik pusulanın 12. yüzyılda Asya'dan Avrupa'ya ulaşmasından önce, Vikinglerin 9-11. yüzyıllarda Kuzey Atlantik boyunca yaptıkları kapsamlı seferlerde benzer bir cihazdan ("güneş taşı") yararlandıkları tartışmalı bir şekilde öne sürülmüştür. Gökyüzü pusulasıyla bağlantılı olan "kutup saati" 19. yüzyılın sonlarında Charles Wheatstone tarafından icat edilmiştir. ⓘ

Ekran teknolojileri

Sıvı kristal ekran (LCD) teknolojisinin prensibi, doğrusal polarizasyon ekseninin sıvı kristal dizisi tarafından döndürülmesine dayanır. Arka ışıktan (veya arka ışık içermeyen veya gerektirmeyen cihazlarda arka yansıtıcı katmandan) gelen ışık önce doğrusal bir polarizasyon tabakasından geçer. Bu polarize ışık, pikseller halinde (bir TV veya bilgisayar monitörü için) veya yedi segmentli ekran ya da belirli bir ürün için özel semboller içeren bir ekran gibi başka bir formatta düzenlenebilen gerçek sıvı kristal tabakadan geçer. Sıvı kristal katman, esasen küçük sarmallardan oluşan tutarlı bir sağ (veya sol) elli kiralite ile üretilir. Bu, dairesel çift kırılmaya neden olur ve doğrusal polarizasyon durumunda 90 derecelik bir dönüş olacak şekilde tasarlanmıştır. Bununla birlikte, bir hücre boyunca bir voltaj uygulandığında, moleküller düzleşerek dairesel çift kırılmayı azaltır veya tamamen kaybeder. Ekranın bakan tarafında, genellikle aktif katmanın arkasındakinden 90 derece yönlenmiş başka bir doğrusal polarizasyon tabakası bulunur. Bu nedenle, dairesel çift kırılma yeterli bir voltaj uygulanarak ortadan kaldırıldığında, iletilen ışığın polarizasyonu ön polarizöre dik açılarda kalır ve piksel karanlık görünür. Ancak voltaj olmadığında, polarizasyonun 90 derecelik dönüşü, ön polarizörün ekseniyle tam olarak eşleşmesine neden olarak ışığın geçmesine izin verir. Ara gerilimler polarizasyon ekseninde ara dönüşler yaratır ve piksel ara bir yoğunluğa sahip olur. Bu prensibe dayalı ekranlar yaygındır ve şu anda televizyonların, bilgisayar monitörlerinin ve video projektörlerinin büyük çoğunluğunda kullanılmaktadır ve önceki CRT teknolojisini esasen kullanılmaz hale getirmiştir. LCD ekranların çalışmasında polarizasyonun kullanılması, polarize güneş gözlüğü takan biri tarafından hemen fark edilir ve genellikle ekranı okunamaz hale getirir. ⓘ

Tamamen farklı bir anlamda, polarizasyon kodlaması, 3D filmler için kullanılan stereoskopik ekranlarda sol ve sağ göze ayrı görüntüler sunmak için önde gelen (ancak tek değil) yöntem haline gelmiştir. Bu, ya ortogonal olarak yönlendirilmiş polarizasyon filtrelerine sahip iki farklı projektörden ya da daha tipik olarak zaman çoğullamalı polarizasyona sahip tek bir projektörden (birbirini izleyen kareler için hızlı bir şekilde değişen polarizasyon cihazı) yansıtılan her bir göze yönelik ayrı görüntüleri içerir. Uygun polarizasyon filtrelerine sahip polarize 3D gözlükler, her bir gözün yalnızca amaçlanan görüntüyü almasını sağlar. Tarihsel olarak bu tür sistemler doğrusal polarizasyon kodlaması kullanmıştır çünkü ucuzdur ve iyi bir ayrım sağlar. Ancak dairesel polarizasyon iki görüntünün ayrılmasını başın eğilmesine karşı duyarsız hale getirir ve günümüzde RealD sistemi gibi 3 boyutlu film gösterimlerinde yaygın olarak kullanılmaktadır. Bu tür görüntülerin yansıtılması, yansıtılan ışığın yansıma halindeyken polarizasyonunu koruyan ekranlar gerektirir (gümüş ekranlar gibi); normal dağınık beyaz bir projeksiyon ekranı, yansıtılan görüntülerin depolarizasyonuna neden olarak bu uygulama için uygun değildir. ⓘ

Artık kullanılmamasına rağmen, CRT bilgisayar ekranları cam zarfın yansımasından muzdaripti, oda ışıklarından parlamaya ve sonuç olarak zayıf kontrasta neden oluyordu. Bu sorunu iyileştirmek için çeşitli yansıma önleyici çözümler kullanıldı. Çözümlerden biri dairesel polarize ışığın yansıması prensibini kullanıyordu. Ekranın önündeki dairesel polarize filtre, (diyelim ki) sadece sağ dairesel polarize oda ışığının iletilmesini sağlar. Şimdi, sağ dairesel polarize ışık (kullanılan konvansiyona bağlı olarak) +z yönünde yayılırken elektrik (ve manyetik) alan yönü saat yönünde döner. Yansıma üzerine, alan hala aynı dönüş yönüne sahiptir, ancak şimdi yayılma -z yönündedir ve yansıyan dalgayı sol dairesel polarize yapar. Yansıtıcı camın önüne yerleştirilen sağ dairesel polarizasyon filtresi ile camdan yansıyan istenmeyen ışık, bu filtre tarafından engellenen çok polarizasyon durumunda olacak ve yansıma sorununu ortadan kaldıracaktır. Dairesel polarizasyonun yansımada tersine dönmesi ve yansımaların bu şekilde ortadan kalkması, iki mercekte sol ve sağ el dairesel polarizasyon kullanan 3 boyutlu film gözlüklerini takarken aynaya bakarak kolayca gözlemlenebilir. Bir göz kapatıldığında, diğer göz kendisini göremediği bir yansıma görecektir; bu mercek siyah görünecektir. Ancak diğer mercek (kapalı gözün) doğru dairesel polarizasyona sahip olacak ve kapalı gözün açık göz tarafından kolayca görülmesini sağlayacaktır. ⓘ

Radyo iletimi ve alımı

İletim ya da alım için kullanılan tüm radyo (ve mikrodalga) antenleri özünde polarizedir. Belirli bir polarizasyonda yayın yaparlar (ya da bu polarizasyondan sinyal alırlar), karşıt polarizasyona karşı tamamen duyarsızdırlar; bazı durumlarda bu polarizasyon yönün bir fonksiyonudur. Çoğu anten nominal olarak doğrusal polarizasyonludur, ancak eliptik ve dairesel polarizasyon da mümkündür. Optikte olduğu gibi, bir radyo dalgasının "polarizasyonu" elektrik alanının polarizasyonu olarak anlaşılır; doğrusal polarizasyonlu bir dalga için manyetik alan ona göre 90 derecelik bir rotasyondadır. ⓘ

Antenlerin büyük çoğunluğu doğrusal polarizasyonludur. Aslında simetri açısından bakıldığında, gözlemciyi de içine alan bir düzlemde tamamen uzanan bir antenin polarizasyonunun sadece bu düzlem yönünde olabileceği gösterilebilir. Bu durum pek çok durumda geçerlidir ve böyle bir antenin yayılma yönündeki polarizasyonunu kolayca çıkarabiliriz. Dolayısıyla, yatay iletkenlere sahip tipik bir çatı Yagi ya da log-periyodik anten, ikinci bir istasyondan ufka doğru bakıldığında, zorunlu olarak yatay polarizasyonludur. Ancak bir anten elemanı olarak kullanılan dikey bir "kamçı anten" ya da AM yayın kulesi (yine yatay olarak yer değiştirmiş gözlemciler için) dikey polarizasyonda yayın yapacaktır. Dört kolu yatay düzlemde olan bir turnike anten de aynı şekilde ufka doğru yatay polarizasyonlu ışıma yapar. Bununla birlikte, aynı turnike anten "eksenel modda" kullanıldığında (aynı yatay yönelimli yapı için yukarı doğru) ışıması dairesel polarizasyonludur. Ara yüksekliklerde ise eliptik polarizasyonludur. ⓘ

Polarizasyon radyo iletişiminde önemlidir, çünkü örneğin dikey polarizasyonlu bir yayını almak için yatay polarizasyonlu bir anten kullanılmaya çalışılırsa, sinyal gücü önemli ölçüde azalacaktır (ya da çok kontrollü koşullar altında sıfıra indirilecektir). Bu ilke uydu televizyonunda sabit bir frekans bandı üzerinde kanal kapasitesini iki katına çıkarmak için kullanılır. Aynı frekans kanalı zıt polarizasyonlarda yayınlanan iki sinyal için kullanılabilir. Alıcı anteni polarizasyonlardan birine ya da diğerine göre ayarlayarak, sinyallerden biri diğerinden etkilenmeden seçilebilir. ⓘ

Özellikle zeminin varlığı nedeniyle, yatay ve dikey polarizasyonlar arasında yayılmada (ve ayrıca TV gölgelenmesinden sorumlu yansımalarda) bazı farklılıklar vardır. AM ve FM radyo yayınları genellikle dikey polarizasyon kullanırken, televizyon yatay polarizasyon kullanır. Özellikle düşük frekanslarda yatay polarizasyondan kaçınılır. Bunun nedeni yatay olarak polarize edilmiş bir dalganın fazının yer tarafından yansıtıldığında tersine dönmesidir. Yatay yönde uzaktaki bir istasyon hem doğrudan hem de yansıyan dalgayı alacaktır, dolayısıyla bunlar birbirini iptal etme eğilimindedir. Bu sorun dikey polarizasyon ile önlenir. Polarizasyon, radar darbelerinin iletimi ve radar yansımalarının aynı ya da farklı bir anten tarafından alınmasında da önemlidir. Örneğin, radar darbelerinin yağmur damlaları tarafından geri saçılması dairesel polarizasyon kullanılarak önlenebilir. Yukarıda tartışıldığı gibi, dairesel polarizasyonlu ışığın speküler yansıması nasıl polarizasyonun yönünü tersine çeviriyorsa, aynı ilke yağmur damlaları gibi bir dalga boyundan çok daha küçük nesneler tarafından saçılma için de geçerlidir. Öte yandan, bu dalganın düzensiz bir metal nesne (uçak gibi) tarafından yansıtılması tipik olarak polarizasyonda bir değişikliğe ve aynı anten tarafından geri dönen dalganın (kısmi) alınmasına neden olacaktır. ⓘ

İyonosferdeki serbest elektronların etkisi, dünyanın manyetik alanı ile birlikte, Faraday rotasyonuna, bir tür dairesel çift kırılmaya neden olur. Bu, aşağıda belirtildiği gibi yıldızlararası uzayda elektronlar tarafından doğrusal kutuplaşma eksenini döndürebilen aynı mekanizmadır. Böyle bir plazmanın neden olduğu Faraday rotasyonunun büyüklüğü düşük frekanslarda büyük ölçüde abartılıdır, bu nedenle uydular tarafından kullanılan daha yüksek mikrodalga frekanslarında etki minimumdur. Ancak iyonosfer tarafından kırıldıktan sonra alınan orta veya kısa dalga yayınlar güçlü bir şekilde etkilenir. Bir dalganın iyonosferden geçtiği yol ve bu yol boyunca dünyanın manyetik alan vektörü tahmin edilemez olduğundan, dikey (veya yatay) polarizasyonla iletilen bir dalga genellikle alıcıda rastgele bir yönde polarizasyona sahip olacaktır. ⓘ

Bir uçağın plastik penceresinden geçen dairesel polarizasyon, 1989 ⓘ

Kutuplaşma ve vizyon

Birçok hayvan ışığın polarizasyonunun bazı bileşenlerini, örneğin doğrusal yatay polarize ışığı algılayabilir. Gökyüzü ışığının doğrusal polarizasyonu her zaman güneşin yönüne dik olduğundan, bu genellikle yön bulma amacıyla kullanılır. Bu yetenek, iletişimsel danslarını yönlendirmek için bu bilgiyi kullanan arılar da dahil olmak üzere böcekler arasında çok yaygındır. Polarizasyon hassasiyeti ahtapot, kalamar, mürekkep balığı ve mantis karidesi türlerinde de gözlemlenmiştir. Son durumda, bir tür polarizasyonun altı ortogonal bileşeninin tümünü ölçer ve optimal polarizasyon görüşüne sahip olduğuna inanılır. İletişim için kullanılan mürekkep balığının hızla değişen, canlı renkli deri desenleri de polarizasyon desenlerini içerir ve mantis karidesinin polarizasyon seçici yansıtıcı dokuya sahip olduğu bilinmektedir. Gökyüzü polarizasyonunun güvercinler tarafından algılandığı ve güvercinlerin yön bulmalarına yardımcı olduğu düşünülmüştür, ancak araştırmalar bunun popüler bir efsane olduğunu göstermektedir. ⓘ

Çıplak insan gözü, araya giren filtrelere ihtiyaç duymadan polarizasyona karşı zayıf bir hassasiyete sahiptir. Polarize ışık, görme alanının merkezine yakın bir yerde Haidinger fırçası adı verilen çok silik bir desen oluşturur. Bu deseni görmek çok zordur, ancak pratik yaparak polarize ışığı çıplak gözle tespit etmeyi öğrenebilirsiniz. ⓘ

Dairesel polarizasyon kullanarak açısal momentum

Elektromanyetik radyasyonun yayılma yönünde belirli bir doğrusal momentum taşıdığı iyi bilinmektedir. Bununla birlikte, ışık dairesel olarak kutuplanmışsa (veya kısmen kutuplanmışsa) belirli bir açısal momentum taşır. Mikrodalgalar gibi daha düşük frekanslarla karşılaştırıldığında, saf dairesel polarizasyonda bile ışıktaki açısal momentum miktarı, aynı dalganın doğrusal momentumuna (veya radyasyon basıncına) kıyasla çok küçüktür ve ölçülmesi bile zordur. Ancak bir deneyde dakikada 600 milyon devire varan hızlara ulaşmak için kullanılmıştır. ⓘ