Radyan

	Radyan ⓘ
Ölçü sistemi:	SI'dan türetilen birim
Neyin birimi	Açı
Sembol:	rad
	Birim dönüşümleri
1 rad	eşittir:
Derece	≈ 57.295°

Radyanın tanımının görsel ifadesi ve

{\pi }

ile ilişkisi. ⓘ

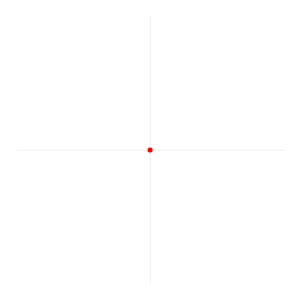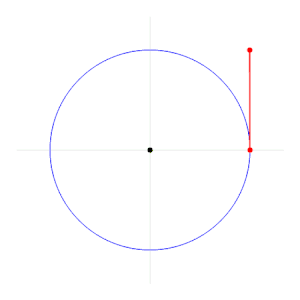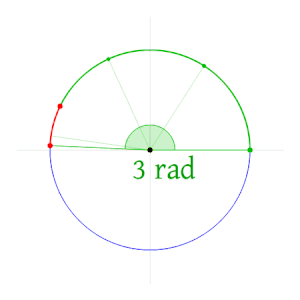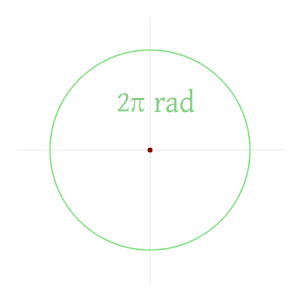
Radyan, bir dairede yarıçap uzunluğundaki yay parçasını gören merkez açıya eşit açı ölçme birimidir. 1 radyan $180 π$ ya da yaklaşık 57,2958 derecedir (57°17′45″). ⓘ

Örneğin, yarıçap değeri 1 m, olan bir çemberde 1 m uzunlukta yayı gören merkez açı 1 radyan'dır. ⓘ

Radyan, açısal ölçünün standart birimidir ve matematiğin birçok alanında kullanılır. Bir açının radyan olarak ölçümü sayısal olarak bir birim dairenin karşılık gelen bir yayının uzunluğuna eşittir, böylece bir radyan 57.3 derecenin hemen altındadır (yay uzunluğu yarıçapa eşit olduğunda). Birim daha önceden bir SI tamamlayıcı birimi idi, ama bu kategori 1995 yılında kaldırıldı ve radyan şimdi bir SI türetilmiş birimi olarak kabul edilir. Tam açı ölçümünün SI birimi steradyandır. Radyan, rad sembolü ile temsil edilir (Unicode-kodu U+33AD ㎭ ). Üst simge c harfi "dairesel ölçüm" için alternatif bir semboldür, ancak bu seyrek kullanılır çünkü bir derece sembolü (°) ile kolayca karıştırılabilir. Yani örneğin bir 1,2 radyan değeri 1,2 rad, 1,2rad ya da 1,2c olarak yazılabilir. ⓘ

Tanım

Bir radyan, bir dairenin merkezinden geçen ve dairenin yarıçapına eşit uzunluktaki bir yayı kesen açı olarak tanımlanır. Daha genel olarak, alttan geçen bir açının radyan cinsinden büyüklüğü, yay uzunluğunun dairenin yarıçapına oranına eşittir; yani $θ = s/r$ , burada $θ$ radyan cinsinden alttan geçen açı, s yay uzunluğu ve r yarıçaptır. Bir dik açı tam olarak $π$ /2 radyandır. ⓘ

Tam bir devir 2

π

radyandır (burada yarıçapı bir ve dolayısıyla çevresi 2

π

olan bir daire ile gösterilmiştir). ⓘ

Bir tam devrin (360 derece) radyan cinsinden büyüklüğü, tüm çevrenin uzunluğunun yarıçapa bölünmesi veya $2 π r / r$ veya 2 $π$ 'dir. Dolayısıyla 2 $π$ radyan 360 dereceye eşittir, yani bir radyan 180/ $π$ derece ≈ 57,295779513082320876 dereceye eşittir. ⓘ

$2 π rad = 360°$ bağıntısı yay uzunluğu formülü kullanılarak türetilebilir, $\ell _{\text{arc}}=2\pi r\left({\tfrac {\theta }{360^{\circ }}}\right)$ ve yarıçapı 1 olan bir çember kullanarak. Radyan, çemberin yarıçapına eşit uzunluktaki bir yayı kesen bir açının ölçüsü olduğundan, $1=2\pi \left({\tfrac {1{\text{ rad}}}{360^{\circ }}}\right)$ . Bu daha da basitleştirilebilir $1={\tfrac {2\pi {\text{ rad}}}{360^{\circ }}}$ . Her iki tarafın 360° ile çarpılması $360° = 2 π rad$ değerini verir. ⓘ

Birim sembolü

Uluslararası Ağırlıklar ve Ölçüler Bürosu ve Uluslararası Standardizasyon Örgütü radyan için rad sembolünü kullanmaktadır. Yüz yıl önce kullanılan alternatif semboller c ("dairesel ölçü" için üst simge c harfi), r harfi veya üst simge ^R'dir, ancak bu varyantlar derece sembolü (°) veya yarıçap (r) ile karıştırılabileceğinden nadiren kullanılmaktadır. Dolayısıyla 1,2 radyan değeri en yaygın olarak 1,2 rad olarak yazılır; diğer gösterimler arasında 1,2 r, 1,2rad, 1,2c veya 1,2^R bulunur. ⓘ

Matematiksel yazımda "rad" sembolü genellikle atlanır. Herhangi bir sembol yokken bir açıyı ölçerken radyan kabul edilir ve derece kastedildiğinde ° derece işareti kullanılır. ⓘ

Dönüşümler

Derece ve radyan arasında dönüşüm yapmak için bir çizelge ⓘ

Ortak açıların dönüştürülmesi ⓘ
Dönüşler	Radyanlar	Dereceler	Gradyanlar ya da gonlar
0 dönüş	0 rad	0°	0^g
1/24 dönüş	$π$ /12 rad	15°	16+2/3^g
1/16 tur	$π$ /8 rad	22.5°	25^g
1/12 dönüş	$π$ /6 rad	30°	33+1/3^g
1/10 dönüş	$π$ /5 rad	36°	40^g
1/8 tur	$π$ /4 rad	45°	50^g
1/2 $π$ dönüş	1 rad	c. 57.3°	c. 63.7^g
1/6 dönüş	$π$ /3 rad	60°	66+2/3^g
1/5 dönüş	2 $π$ /5 rad	72°	80^g
1/4 tur	$π$ /2 rad	90°	100^g
1/3 tur	2 $π$ /3 rad	120°	133+1/3^g
2/5 dönüş	4 $π$ /5 rad	144°	160^g
1/2 tur	$π$ rad	180°	200^g
3/4 tur	3 $π$ /2 rad	270°	300^g
1 dönüş	2 $π$ rad	360°	400^g

Tabloda bazı yaygın açıların dönüştürülmesi gösterilmektedir. ⓘ

Birimler	Değerler ⓘ
Devir	0	124	112	110	18	16	15	14	13	25	12	34	1
Radyan	0	112π	16π	15π	14π	13π	25π	12π	23π	45π	π	32π	2π
Derece	0°	15°	30°	36°	45°	60°	72°	90°	120°	144°	180°	270°	360°
Grad	0^g	1623^g	3313^g	40^g	50^g	6623^g	80^g	100^g	13313^g	160^g	200^g	300^g	400^g

Radyan ve derece arasında dönüşüm

Belirtildiği gibi, bir radyan şuna eşittir ${180^{\circ }}/{\pi }$ . Böylece, radyandan dereceye dönüştürmek için ${180^{\circ }}/{\pi }$ . ⓘ

{\text{angle in degrees}}={\text{angle in radians}}\cdot {\frac {180^{\circ }}{\pi }}

ⓘ

Örneğin:

1{\text{ rad}}=1\cdot {\frac {180^{\circ }}{\pi }}\approx 57.2958^{\circ }

2.5{\text{ rad}}=2.5\cdot {\frac {180^{\circ }}{\pi }}\approx 143.2394^{\circ }

{\frac {\pi }{3}}{\text{ rad}}={\frac {\pi }{3}}\cdot {\frac {180^{\circ }}{\pi }}=60^{\circ }

ⓘ

Tersine, dereceden radyana dönüştürmek için, ile çarpın ${\pi }/{180^{\circ }}$ . ⓘ

{\text{angle in radians}}={\text{angle in degrees}}\cdot {\frac {\pi }{180^{\circ }}}

ⓘ

Örneğin:

1^{\circ }=1^{\circ }\cdot {\frac {\pi }{180^{\circ }}}\approx 0.0175{\text{ rad}}

$23^{\circ }=23^{\circ }\cdot {\frac {\pi }{180^{\circ }}}\approx 0.4014{\text{ rad}}$ ⓘ

Radyanlar, radyan sayısı 2 $π$ 'ye bölünerek dönüşlere (tam devir) dönüştürülebilir. ⓘ

Radyandan dereceye dönüştürme türevi

Bir dairenin çevresinin uzunluğu şu şekilde verilir $2\pi r$ , nerede $r$ dairenin yarıçapıdır. ⓘ

Dolayısıyla aşağıdaki eşdeğer ilişki doğrudur: $360^{\circ }r\iff 2\pi r$ [a'dan beri $360^{\circ }$ tam bir daire çizmek için süpürme gereklidir] ⓘ

Radyanın tanımına göre, tam bir daire temsil eder:

{\frac {2\pi r}{r}}{\text{ rad}}

ⓘ

=2\pi {\text{ rad}}

ⓘ

Yukarıdaki her iki ilişkinin birleştirilmesi:

2\pi {\text{ rad}}=360^{\circ }

ⓘ

\Rrightarrow 1{\text{ rad}}={\frac {360^{\circ }}{2\pi }}

ⓘ

\Rrightarrow 1{\text{ rad}}={\frac {180^{\circ }}{\pi }}

ⓘ

Radyan ve gradyan arasında dönüşüm

$2\pi$ radyan bir tura eşittir, bu da tanım gereği 400 gradyandır (400 gon veya 400g). Yani, radyandan gradyana dönüştürmek için aşağıdakilerle çarpın $200^{\text{g}}/\pi$ ile çarpın ve gradyandan radyana dönüştürmek için $\pi /200^{\text{g}}$ . Örneğin, ⓘ

1.2{\text{ rad}}=1.2\cdot {\frac {200^{\text{g}}}{\pi }}\approx 76.3944^{\text{g}}

50^{\text{g}}=50^{\text{g}}\cdot {\frac {\pi }{200^{\text{g}}}}\approx 0.7854{\text{ rad}}

ⓘ

Radyan cinsinden ölçüm yapmanın avantajları

Radyan cinsinden ölçülen bazı yaygın açılar. Bu diyagramdaki tüm büyük çokgenler düzgün çokgenlerdir. ⓘ

Kalkülüs ve matematiğin pratik geometri dışındaki diğer dallarının çoğunda açılar evrensel olarak radyan cinsinden ölçülür. Bunun nedeni, radyanın bir dizi önemli sonucun daha zarif bir şekilde formüle edilmesini sağlayan matematiksel bir "doğallığa" sahip olmasıdır. ⓘ

En önemlisi, trigonometrik fonksiyonları içeren analiz sonuçları, fonksiyonların argümanları radyan cinsinden ifade edildiğinde zarif bir şekilde ifade edilebilir. Örneğin, radyan kullanımı basit limit formülüne yol açar ⓘ

\lim _{h\rightarrow 0}{\frac {\sin h}{h}}=1,

ⓘ

dahil olmak üzere matematikteki diğer birçok özdeşliğin temelini oluşturur. ⓘ

{\frac {d}{dx}}\sin x=\cos x

{\frac {d^{2}}{dx^{2}}}\sin x=-\sin x.

ⓘ

Bu ve diğer özellikleri nedeniyle, trigonometrik fonksiyonlar, fonksiyonların geometrik anlamlarıyla açıkça ilgili olmayan matematiksel problemlerin çözümlerinde ortaya çıkar (örneğin, diferansiyel denklemin çözümleri ${\tfrac {d^{2}y}{dx^{2}}}=-y$ , integralin değerlendirilmesi $\textstyle \int {\frac {dx}{1+x^{2}}},$ ve benzeri). Tüm bu durumlarda, fonksiyonların argümanlarının en doğal olarak geometrik bağlamlarda açıların radyan ölçümüne karşılık gelen biçimde yazıldığı görülür. ⓘ

Trigonometrik fonksiyonlar radyan kullanıldığında da basit ve zarif seri açılımlarına sahiptir. Örneğin, x radyan cinsinden olduğunda, sin x için Taylor serisi olur:

\sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots .

ⓘ

Eğer x derece cinsinden ifade edilseydi, seri $π$ /180'in kuvvetlerini içeren dağınık faktörler içerecekti: x derece sayısı ise, radyan sayısı y = $π$ x / 180, yani ⓘ

\sin x_{\mathrm {deg} }=\sin y_{\mathrm {rad} }={\frac {\pi }{180}}x-\left({\frac {\pi }{180}}\right)^{3}\ {\frac {x^{3}}{3!}}+\left({\frac {\pi }{180}}\right)^{5}\ {\frac {x^{5}}{5!}}-\left({\frac {\pi }{180}}\right)^{7}\ {\frac {x^{7}}{7!}}+\cdots .

ⓘ

Benzer bir şekilde, sinüs ve kosinüs fonksiyonları ile üstel fonksiyon arasındaki matematiksel olarak önemli ilişkiler (örneğin, Euler formülüne bakınız), fonksiyonların argümanları radyan cinsinden olduğunda zarif bir şekilde ifade edilebilir (ve aksi takdirde dağınıktır). ⓘ

Tarih

Bir açının derecesinin aksine radyan ölçüsü kavramı normalde 1714 yılında Roger Cotes'a atfedilir. Radyanı adı dışında her şeyiyle tanımlamış ve açısal ölçü birimi olarak doğallığını kabul etmiştir. Radyan terimi yaygınlaşmadan önce, bu birim genellikle bir açının dairesel ölçüsü olarak adlandırılıyordu. ⓘ

Açıları yay uzunluğuna göre ölçme fikri diğer matematikçiler tarafından zaten kullanılıyordu. Örneğin, el-Kaşi (1400 civarı) birim olarak çap parçalarını kullanmıştır; burada bir çap parçası 1/60 radyandır. Ayrıca çap parçasının seksajimal alt birimlerini de kullanmışlardır. ⓘ

Radyan terimi ilk kez 5 Haziran 1873'te James Thomson (Lord Kelvin'in kardeşi) tarafından Queen's College, Belfast'ta hazırlanan sınav sorularında basılı olarak ortaya çıktı. Bu terimi 1871 gibi erken bir tarihte kullanmıştı. 1869'da o zamanlar St Andrews Üniversitesi'nden olan Thomas Muir rad, radyal ve radyan terimleri arasında bocalamıştı. Muir, 1874 yılında James Thomson ile yaptığı istişarenin ardından radyanı benimsemiştir. Radyan adı bundan sonra bir süre evrensel olarak benimsenmedi. Longmans' School Trigonometry 1890'da yayınlandığında hala radyan dairesel ölçü olarak adlandırılıyordu. ⓘ

SI birimi olarak tarihçe

Paul Quincey ve diğerlerinin yazdığı gibi, "açıların Uluslararası Birimler Sistemi (SI) içindeki statüsü uzun zamandır bir tartışma ve karışıklık kaynağı olmuştur." 1960 yılında CGPM SI'yı kurdu ve radyan, steradyan ile birlikte "tamamlayıcı birim" olarak sınıflandırıldı. CGPM radyanın temel birim mi yoksa türetilmiş birim mi olduğu konusunda bir karara varamadığından, bu özel sınıf resmi olarak "ya temel birimler ya da türetilmiş birimler" olarak kabul edildi. Richard Nelson şöyle yazmaktadır: "[Ek birimlerin sınıflandırılmasındaki] bu belirsizlik, bunların doğru yorumlanması konusunda hararetli bir tartışmaya yol açmıştır." Mayıs 1980'de Birimler Danışma Komitesi (CCU), $α 0 = 1 rad$ sabitini kullanarak radyanı bir SI temel birimi haline getirme önerisini değerlendirdi, ancak mevcut uygulamada bir kargaşayı önlemek için bu öneriyi geri çevirdi. ⓘ

Ekim 1980'de CGPM, "aynı zamanda tutarlı ve kullanışlı olan ve düzlem açı ve katı açı niceliklerinin temel nicelikler olarak kabul edilebileceği [bir formalizm] bulunmadığı" ve "[radyan ve steradyanı SI temel birimleri olarak ele alma olasılığının] yalnızca yedi temel birime dayanan SI'nın iç tutarlılığını tehlikeye attığı" temelinde, CGPM'nin SI'dan türetilmiş birimler için ifadelerde bunları kullanma veya kullanmama özgürlüğüne izin verdiği boyutsuz türetilmiş birimler olduğuna karar verdi. 1995 yılında CGPM tamamlayıcı birimler sınıfını ortadan kaldırmış ve radyan ve steradyanı "adları ve sembolleri uygun olduğu ölçüde diğer SI türetilmiş birimleri için ifadelerde kullanılabilen ancak kullanılması gerekmeyen boyutsuz türetilmiş birimler" olarak tanımlamıştır. . Mikhail Kalinin 2019'da yazdığı yazıda 1980 CGPM kararını "temelsiz" olarak eleştirmiş ve 1995 CGPM kararının tutarsız argümanlar kullandığını ve "SI'nın ifadelerinde çok sayıda tutarsızlık, tutarsızlık ve çelişki" ortaya koyduğunu söylemiştir. ⓘ

CCU'nun 2013 toplantısında Peter Mohr, radyanın bir temel birim yerine boyutsuz bir birim olarak tanımlanmasından kaynaklandığı iddia edilen tutarsızlıklar üzerine bir sunum yapmıştır. CCU Başkanı Ian M. Mills bunun "zorlu bir sorun" olduğunu ilan etti ve CCU SI'da Açılar ve Boyutsuz Nicelikler Çalışma Grubu kuruldu. CCU en son 2021 yılında toplandı, ancak bir fikir birliğine varamadı. Az sayıda üye radyanın temel birim olması gerektiğini güçlü bir şekilde savundu, ancak çoğunluk statükonun kabul edilebilir olduğunu veya değişikliğin çözeceğinden daha fazla soruna neden olacağını düşünüyordu. Diğer faaliyetlerin yanı sıra, "SI ek birimlerinin tarihsel kullanımını gözden geçirmek ve yeniden kullanılmasının faydalı olup olmayacağını değerlendirmek" için bir görev grubu kurulmuştur. ⓘ

Boyutsal analiz

Radyan $θ = s/r$ olarak tanımlanır; burada $θ$ radyan cinsinden alttan geçen açı, s yay uzunluğu ve r yarıçaptır. Bir radyan, $s=r$ olan açıya karşılık gelir, dolayısıyla 1 radyan = 1 m/m'dir. Bununla birlikte, $\mathrm {rad}$ sadece açıları ifade etmek için kullanılmalıdır, genel olarak uzunluk oranlarını ifade etmek için değil. Dairesel bir sektörün alanı $θ = 2 A /r 2$ kullanılarak yapılan benzer bir hesaplama 1 radyanı 1 m²/m² olarak verir. Temel gerçek, radyanın 1'e eşit boyutsuz bir birim olmasıdır. SI 2019'da radyan buna göre 1 rad = 1 olarak tanımlanır. Matematikte ve bilimin tüm alanlarında radyan birimini kullanmak köklü bir uygulamadır. $\mathrm {rad} =1$ . 1993 yılında AAPT Metrik Komitesi, radyanın sadece diğer açı ölçüleri kullanıldığında farklı sayısal değerler elde edilecekse, örneğin açı ölçüsü (rad), açısal hız (rad/s), açısal ivme (rad/s²) ve burulma sertliği (N⋅m/rad) gibi büyüklüklerde açıkça görünmesi gerektiğini, tork (N⋅m) ve açısal momentum (kg⋅m²/s) büyüklüklerinde görünmemesi gerektiğini belirtmiştir. ⓘ

Giacomo Prando, "mevcut durum kaçınılmaz olarak fiziksel denklemlerin boyutsal analizinde radyanın hayalet gibi görünmesine ve kaybolmasına yol açıyor" diyor. Örneğin, bir makaradan iple sarkan bir kütle $y= rθ$ santimetre kadar yükselir ya da alçalır; burada r makaranın santimetre cinsinden yarıçapı, $θ$ ise makaranın radyan cinsinden döndüğü açıdır. r ile $θ$ çarpıldığında radyan birimi sonuçtan kaybolur. Benzer şekilde, yuvarlanan bir tekerleğin açısal hızı için formülde, $ω =v/r$ , radyan $ω$ birimlerinde görünür ancak sağ tarafta görünmez. Anthony French bu olguyu "mekanik öğretiminde süregelen bir sorun" olarak adlandırmaktadır. Oberhofer, boyutsal analiz sırasında radyanı görmezden gelme ve geleneksel ve bağlamsal bilgiye göre birimlere radyan ekleme veya çıkarma şeklindeki tipik tavsiyenin "pedagojik olarak tatmin edici olmadığını" söylüyor. ⓘ

En az bir düzine bilim insanı, 1936 gibi erken bir tarihte ve 2022 gibi yakın bir tarihte, radyanı kendi "açı" boyutunu tanımlayan temel bir ölçü birimi olarak ele almak için önerilerde bulunmuştur. Quincey'nin önerilere ilişkin incelemesi iki öneri sınıfının ana hatlarını çizmektedir. İlk seçenek yarıçap birimini radyan başına metre olarak değiştirir, ancak bu bir dairenin alanı için boyutsal analizle uyumsuzdur, $πr 2$ . Diğer seçenek ise boyutsal bir sabit getirmektir. Quincey'e göre bu yaklaşım SI'ye kıyasla "mantıksal olarak titizdir", ancak "bilinen birçok matematiksel ve fiziksel denklemin değiştirilmesini" gerektirir. ⓘ

Quincey özellikle Torrens'in ε₀ sabitine benzer bir şekilde 1 ters radyana (1 rad-1) eşit bir $η$ sabiti getirme önerisini tanımlamaktadır. Bu değişiklikle, bir dairenin merkezinden geçen açı için formül, $s = rθ$ , $s = ηrθ$ olacak şekilde değiştirilir ve $θ$ açısının sinüsü için Taylor serisi olur:

\operatorname {Sin} \theta =\sin _{\text{rad}}(\eta \theta )=\eta \theta -{\frac {(\eta \theta )^{3}}{3!}}+{\frac {(\eta \theta )^{5}}{5!}}-{\frac {(\eta \theta )^{7}}{7!}}+\cdots .

ⓘ

Büyük harfle yazılan fonksiyon $\operatorname {Sin}$ açı boyutunda bir argüman alan ve ifade edilen birimlerden bağımsız olan "tam" fonksiyon iken $\sin _{\text{rad}}$ argümanının radyan cinsinden olduğunu varsayan saf sayılar üzerindeki geleneksel fonksiyondur. $\operatorname {Sin}$ olarak gösterilebilir $\sin$ tam formun kastedildiği açıksa. ⓘ

SI bu çerçeveye göre, $η$ = 1 denkleminin geçerli olduğu varsayılan doğal bir birim sistemi veya benzer şekilde 1 rad = 1 olarak düşünülebilir. Bu radyan konvansiyonu, matematiksel formüllerde $η$ 'nin ihmal edilmesine izin verir. ⓘ

Açı için boyutsal bir sabit "oldukça gariptir" ve boyutsal sabiti eklemek için denklemleri değiştirmenin zorluğu muhtemelen yaygın kullanımı engelleyecektir. Radyanı temel birim olarak tanımlamak, daha uzun denklemlerin dezavantajının minimum olduğu yazılımlar için faydalı olabilir. Örneğin, Boost units kütüphanesi açı birimlerini plane_angle boyutuyla tanımlar ve Mathematica'nın birim sistemi de benzer şekilde açıları bir açı boyutuna sahip olarak kabul eder. ⓘ

Fizikte kullanım

Radyan, açısal ölçümler gerektiğinde fizikte yaygın olarak kullanılır. Örneğin, açısal hız tipik olarak saniye başına radyan (rad/s) cinsinden ölçülür. Saniyede bir devir, saniyede 2 $π$ radyana eşittir. ⓘ

Benzer şekilde, açısal ivme genellikle saniye başına radyan cinsinden ölçülür (rad/s²). ⓘ

Boyutsal analiz amacıyla, açısal hız ve açısal ivme birimleri sırasıyla s-1 ve s-2'dir. ⓘ

Benzer şekilde, iki dalganın faz farkı da radyan cinsinden ölçülebilir. Örneğin, iki dalganın faz farkı (n⋅2 $π$ ) radyan ise, burada n bir tamsayıdır, bunlar fazda kabul edilirken, iki dalganın faz farkı (n⋅2 $π$ + $π$ ) ise, burada n bir tamsayıdır, bunlar antifazda kabul edilir. ⓘ

Radyan birimlerin katları

Metrik ön eklerde radyan kullanımı sınırlıdır ve matematikte hiç yoktur. bir mili-radyan (mrad) bir radyanın binde biridir ve bir mikroradyan (urad ya da μrad) bir radyanın milyonda biridir, yani 103 mrad = 106 urad = 1 rad. Bir dairede 2π × 1000 mili-radyan (≈ 6283.185 mrad) vardır. Böylece trigonometrik bir mili-radyan bir dairenin 1⁄6283 ‘ünün hemen altındadır. Bir dairenin açısal ölçümünün bu "gerçek" trigonometrik birimi (Stadiametrik) menzil bulucu kullanan teleskobik görüş üreticileri tarafından kullanılmaktadır. Lazer ışınlarının sapması da genellikle mili-radyan cinsinden ölçülür. Trigonometrik mili-radyanın (0.001 rad) (açısal) mil olarak bilinen bir yaklaştırması NATO ve diğer askeri kuruluşlar tarafından atış tekniği ve hedeflemede kullanılmaktadır. Her açısal mil bir dairenin 1⁄6400 ‘ünü temsil eder ve trigonometrik mili-radyandan 1-⅞% daha küçüktür. Genelde hedefleme işlerinde bulunan küçük açılar için hesaplamada 6400 sayısını kullanma kolaylığı, neden olduğu küçük matematiksel hatalardan ağır basar. Geçmişte diğer atış tekniği sistemlerinde 1⁄2000π’e farklı yaklaştırmalar kullanmıştır. Örneğin İsveç 1⁄6300 ‘i kullanmıştır ve SSCB 1⁄6000’i kullanmıştır. Mili-radyana dayalı olarak NATO mili 1000 m ‘lik bir menzilde kabaca 1 m ‘dir (bu kadar küçük açılarda eğrilik ihmal edilebilir). ⓘ

Mikroradyan (μrad) ve nanoradyan (nrad) gibi küçük birimler astronomide kullanılır ve aynı zamanda lazerlerin ışın kalitesini ultra-düşük sapma ile ölçmek için de kullanılabilir. Benzer şekilde, mili- ‘den daha küçük önekler son derece küçük açıların ölçülmesinde potansiyel olarak kullanışlıdır. ⓘ

Radyan ⓘ
Ölçü sistemi:	SI'dan türetilen birim
Neyin birimi	Açı
Sembol:	rad
Birim dönüşümleri
1 rad	eşittir:
Derece	≈ 57.295°