Kaldıraç

Arşimet'in formüle ettiği kaldıraçlar, destek noktası da denilen sabit bir nokta etrafında dönebilen sistemlere denir. Kaldıracın etrafında döndüğü noktaya destek denir. Uygulanan kuvvetin destek noktasına olan uzaklığına kuvvet kolu, yük ile destek arasındaki uzaklığa yük kolu denir. Bir kaldıraçta kuvvet kolu, yük kolundan ne kadar uzun olursa, bu kaldıraçla kaldırılabilecek yük de o kadar büyük olur. ⓘ

Dengede olan bir kaldıraçta, kuvvetle kuvvet kolunun çarpımı, yükle yük kolunun çarpımına eşittir. Buna kaldıraç bağıntısı denir. ⓘ

• Kuvvet .(x)Kuvvet kolu = Yük .(x) Yük kolu ⓘ

Kaldıraçlar, destek noktasının bulunduğu yere göre çift ve tek taraflı kaldıraç olmak üzere iki gruba ayrılır. ⓘ

• Çift Taraflı Kaldıraç

Desteğin arada olduğu kaldıraçlara denir. Kuvvetin yönünü değiştirir, kuvvetten kazanç sağlar. Günlük hayatta çift taraflı kaldıraca benzer pek çok araç kullanırız. Örneğin makas, pense, levye, kayık küreği desteğin arada, tahterevalli, eşit kollu terazi desteğin ortada olduğu kaldıraca benzer araçlardır. ⓘ

• Tek Taraflı Kaldıraç ⓘ

Desteğin uçta olduğu kaldıraçlardır. İki çeşittir:

1. Desteğin uçta, yükün ortada olduğu kaldıraç. Kuvvetten kazanç, yoldan kayıp vardır. Desteğin uçta, yükün ortada olduğu kaldıraçlara örnekler; el arabası, fındık kıracağı, gazoz açacağı,
2. Desteğin uçta, kuvvetin ortada olduğu kaldıraç. Yoldan kazanç, kuvvetten kayıp vardır. Bu çeşit kaldıraca örnekler; cımbız, maşa, insan çenesi, iş makinelerinin pistonla çalışan kolları, ön kollarımız. ⓘ

Kaldıraçta Kuvvet Kazancı: ⓘ

Basit makinelerde kuvvet kazancı, yükün kuvvete oranı olarak ifade edilir. ⓘ

• yük x yük kolu = kuvvet x kuvvet kolu olduğuna göre,
• kuvvet kazancı = Yük / Kuvvet = Kuvvet Kolu / Yük Kolu olarak yazılabilir. ⓘ

Kuvvet, desteğe yükten daha uzak olduğunda kuvvet kolu daha uzun olduğu için kuvvetten kazanç vardır. ⓘ

Yük, desteğe kuvvetten daha uzak olduğunda kuvvet kolu daha kısa olduğu için yoldan kazanç vardır. ⓘ

Kol ⓘ
Kaldıraçlar, bir uçta küçük bir mesafeye büyük bir kuvvet uygulayarak diğer uçta daha büyük bir mesafeye sadece küçük bir kuvvet (efor) uygulamak için kullanılabilir.
Sınıflandırma	Basit makine
Bileşenler	dayanak noktası veya pivot, yük ve efor
Örnekler	testere, şişe açacağı, vb.

Etimoloji

"Kaldıraç" kelimesi İngilizceye 1300 civarında Eski Fransızcadan girmiştir, bu dilde kelime levier idi. Bu da "kaldırmak" anlamına gelen lever fiilinin kökünden türemiştir. Bu fiil de Latince levare'ye dayanır ve kendisi de "hafif" ("ağır olmayan") anlamına gelen levis sıfatından türemiştir. Kelimenin birincil kökeni Proto-Hint-Avrupa kökenli legwh- köküdür ve diğer anlamlarının yanı sıra "hafif", "kolay" veya "çevik" anlamına gelir. PIE kökü aynı zamanda İngilizce "light" kelimesinin de ortaya çıkmasına neden olmuştur. ⓘ

Tarihçe

Kaldıraç mekanizmasının en eski kanıtları, ilk kez basit bir terazide kullanıldığı MÖ 5000 dolaylarında antik Yakın Doğu'ya kadar uzanmaktadır. MÖ 4400 dolaylarında eski Mısır'da, en eski yatay çerçeveli dokuma tezgahı için bir ayak pedalı kullanılmıştır. MÖ 3000 dolaylarında Mezopotamya'da (modern Irak), bir kaldıraç mekanizması kullanan vinç benzeri bir cihaz olan shadouf icat edilmiştir. Eski Mısır teknolojisinde, işçiler 100 tondan daha ağır dikilitaşları hareket ettirmek ve kaldırmak için kaldıraç kullanmışlardır. Bu, büyük bloklardaki girintilerden ve kaldıraçlar dışında başka bir amaçla kullanılamayacak olan taşıma çıkıntılarından anlaşılmaktadır. ⓘ

Kaldıraçlarla ilgili kalan en eski yazılar MÖ 3. yüzyıla aittir ve "Bana yeterince uzun bir kaldıraç ve onu yerleştirebileceğim bir dayanak noktası verin, dünyayı hareket ettireyim" diyen Yunan matematikçi Arşimet tarafından sağlanmıştır. ⓘ

Kuvvet ve kaldıraçlar

Dengede bir kaldıraç ⓘ

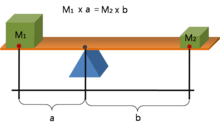
Bir kaldıraç, dayanak noktası olarak adlandırılan bir menteşe veya pivot ile yere bağlanan bir kiriştir. İdeal kaldıraç enerjiyi dağıtmaz veya depolamaz, yani menteşede sürtünme veya kirişte bükülme yoktur. Bu durumda, kola giren güç çıkan güce eşittir ve çıkan gücün giren güce oranı, dayanak noktasından bu güçlerin uygulama noktalarına olan mesafelerin oranıyla verilir. Bu, kaldıraç kanunu olarak bilinir. ⓘ

Bir kaldıracın mekanik avantajı, dayanak noktası etrafındaki momentlerin veya torkun (T) dengesi dikkate alınarak belirlenebilir. Kat edilen mesafe daha büyükse, çıkış kuvveti azalır. ⓘ

$${\begin{aligned}T_{1}&=F_{1}a,\quad \\T_{2}&=F_{2}b\!\end{aligned}}$$

ⓘ

Burada F₁ kola giriş kuvveti ve F₂ çıkış kuvvetidir. a ve b mesafeleri, kuvvetler ve dayanak noktası arasındaki dik mesafelerdir. ⓘ

Tork momentlerinin dengelenmesi gerektiğinden, $T_{1}=T_{2}\!$. Bu yüzden, $F_{1}a=F_{2}b\!$. ⓘ

Kaldıracın mekanik avantajı, çıkış kuvvetinin giriş kuvvetine oranıdır. ⓘ

$$MA={\frac {F_{2}}{F_{1}}}={\frac {a}{b}}.\!$$

ⓘ

Bu ilişki, mekanik avantajın, sürtünme, esneklik veya aşınma nedeniyle herhangi bir kayıp olmadığı varsayılarak, dayanak noktasından kola giriş ve çıkış kuvvetlerinin uygulandığı yerlere olan mesafelerin oranından hesaplanabileceğini göstermektedir. Bu, kaldıraç yataydan herhangi bir konuma değiştikçe hem a hem de b'nin "yatay" mesafesi (yerçekimi çekimine dik) değişse (azalsa) bile doğru kalır. ⓘ

Kaldıraçların sınıflandırılması

Üç sınıf kaldıraç ⓘ

İnsan vücudundan örneklerle üç kaldıraç sınıflandırması ⓘ

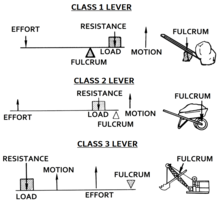
Kaldıraçlar dayanak noktası, efor ve direncin (veya yükün) göreceli konumlarına göre sınıflandırılır. Giriş kuvvetini efor, çıkış kuvvetini ise yük veya direnç olarak adlandırmak yaygındır. Bu, dayanak noktasının, direncin ve eforun göreceli konumlarına göre üç kaldıraç sınıfının tanımlanmasına olanak tanır:

• Sınıf I - Dayanak noktası efor ve direnç arasındadır: Çaba dayanak noktasının bir tarafına, direnç (ya da yük) ise diğer tarafına uygulanır; örneğin tahterevalli, levye ya da makas, terazi, çekiç gibi. Mekanik avantaj 1'den büyük, küçük veya eşit olabilir.
• Sınıf II - Çaba ve dayanak noktası arasındaki direnç (veya yük): Çaba, direncin bir tarafına uygulanır ve dayanak noktası diğer tarafta bulunur, örneğin el arabası, fındık kıracağı, şişe açacağı veya bir arabanın fren pedalı. Yük kolu efor kolundan daha küçüktür ve mekanik avantaj her zaman 1'den büyüktür. Buna kuvvet çarpan kaldıraç da denir.
• Sınıf III - Dayanak noktası ve direnç arasındaki efor: Direnç (veya yük) eforun bir tarafındadır ve dayanak noktası diğer tarafta yer alır, örneğin bir çift cımbız, bir çekiç, bir çift maşa, bir olta veya bir insan kafatasının çene kemiği. Efor kolu yük kolundan daha küçüktür. Mekanik avantaj her zaman 1'den azdır. Buna hız çarpanı kolu da denir. ⓘ

Bu durumlar, 1. sınıf kaldıraç için f dayanak noktasının r ile e arasında olduğu, 2. sınıf kaldıraç için r direncinin f ile e arasında olduğu ve 3. sınıf kaldıraç için e çabasının f ile r arasında olduğu fre 123 anımsatıcısı ile tanımlanır. ⓘ

Bileşik kaldıraç

Bileşik bir kaldıraç, seri olarak hareket eden birkaç kaldıraçtan oluşur: bir kaldıraç sistemindeki bir kaldıraçtan gelen direnç, bir sonraki için efor görevi görür ve böylece uygulanan kuvvet bir kaldıraçtan diğerine aktarılır. Bileşik kaldıraçlara örnek olarak terazi, tırnak makası ve piyano tuşları verilebilir. ⓘ

Malleus, incus ve stapes orta kulakta bulunan ve ses dalgalarını kulak zarından kokleanın oval penceresine aktaran bileşik kaldıraçlar olarak birbirine bağlı küçük kemiklerdir. ⓘ

Kaldıraç kanunu

Kaldıraç, sabit bir noktaya bağlı bir dayanak noktası üzerinde dönen hareketli bir çubuktur. Kaldıraç, dayanak noktasından veya bir pivottan farklı mesafelerde kuvvetler uygulayarak çalışır. ⓘ

Kaldıraç dayanak noktası etrafında dönerken, bu dayanak noktasından daha uzakta olan noktalar dayanak noktasına daha yakın olan noktalardan daha hızlı hareket eder. Bu nedenle, pivottan daha uzaktaki bir noktaya uygulanan kuvvet, daha yakındaki bir noktada bulunan kuvvetten daha az olmalıdır, çünkü güç, kuvvet ve hızın çarpımıdır. ⓘ

Eğer a ve b dayanak noktasından A ve B noktalarına olan uzaklıklar ise ve A'ya uygulanan FA kuvveti giriş ve B'ye uygulanan FB kuvveti çıkış ise, A ve B noktalarının hızlarının oranı a/b ile verilir, böylece çıkış kuvvetinin giriş kuvvetine oranı veya mekanik avantaj ile verilir:

$$MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}}.$$

ⓘ

Bu, Arşimet tarafından geometrik akıl yürütme kullanılarak kanıtlanmış olan kaldıraç yasasıdır. Buna göre, dayanak noktasından giriş kuvvetinin uygulandığı yere (A noktası) olan a mesafesi, dayanak noktasından çıkış kuvvetinin uygulandığı yere (B noktası) olan b mesafesinden büyükse, kaldıraç giriş kuvvetini güçlendirir. Öte yandan, dayanak noktasından giriş kuvvetine olan a mesafesi, dayanak noktasından çıkış kuvvetine olan b mesafesinden daha azsa, kaldıraç giriş kuvvetini azaltır. ⓘ

Bir kaldıracın statik analizinde hızın kullanılması, sanal iş prensibinin bir uygulamasıdır. ⓘ

Sanal iş ve kaldıraç kanunu

Bir kaldıraç, dayanak noktası olarak adlandırılan menteşeli bir mafsal ile bir zemin çerçevesine bağlanmış rijit bir çubuk olarak modellenir. Kaldıraç, çubuk üzerinde rA koordinat vektörü tarafından bulunan bir A noktasına FA giriş kuvveti uygulanarak çalıştırılır. Kaldıraç daha sonra rB tarafından bulunan B noktasında bir çıkış kuvveti FB uygular. Kolun dayanak noktası P etrafındaki dönüşü radyan cinsinden θ dönüş açısı ile tanımlanır. ⓘ

Arşimet kaldıracı, 1824 yılında Londra'da yayınlanan Mechanics Magazine'den gravür ⓘ

Dayanak noktasını tanımlayan P noktasının koordinat vektörü r_P olsun ve uzunlukları tanıtın ⓘ

$$a=|\mathbf {r} _{A}-\mathbf {r} _{P}|,\quad b=|\mathbf {r} _{B}-\mathbf {r} _{P}|,$$

ⓘ

Bunlar sırasıyla dayanak noktasından giriş noktası A'ya ve çıkış noktası B'ye olan uzaklıklardır. ⓘ

Şimdi dayanak noktasından _A ve B noktasına eA ve eB birim vektörlerini tanıtın, böylece ⓘ

$$\mathbf {r} _{A}-\mathbf {r} _{P}=a\mathbf {e} _{A},\quad \mathbf {r} _{B}-\mathbf {r} _{P}=b\mathbf {e} _{B}.$$

ⓘ

A ve B noktalarının hızları aşağıdaki gibi elde edilir ⓘ

$$\mathbf {v} _{A}={\dot {\theta }}a\mathbf {e} _{A}^{\perp },\quad \mathbf {v} _{B}={\dot {\theta }}b\mathbf {e} _{B}^{\perp },$$

ⓘ

Burada e_A^⊥ ve eB^⊥ sırasıyla e_A ve eB'ye dik birim vektörlerdir. ⓘ

θ açısı, kaldıracın konfigürasyonunu tanımlayan genelleştirilmiş koordinattır ve bu koordinatla ilişkili genelleştirilmiş kuvvet şu şekilde verilir ⓘ

$$F_{\theta }=\mathbf {F} _{A}\cdot {\frac {\partial \mathbf {v} _{A}}{\partial {\dot {\theta }}}}-\mathbf {F} _{B}\cdot {\frac {\partial \mathbf {v} _{B}}{\partial {\dot {\theta }}}}=a(\mathbf {F} _{A}\cdot \mathbf {e} _{A}^{\perp })-b(\mathbf {F} _{B}\cdot \mathbf {e} _{B}^{\perp })=aF_{A}-bF_{B},$$

ⓘ

Burada F_A ve FB, PA ve PB radyal segmentlerine dik olan kuvvetlerin bileşenleridir. Sanal iş ilkesi, dengede genelleştirilmiş kuvvetin sıfır olduğunu belirtir, yani ⓘ

$$F_{\theta }=aF_{A}-bF_{B}=0.\,\!$$

ⓘ

Basit kaldıraç, dayanak ve dikey direkler ⓘ

_Böylece, FB çıkış kuvvetinin F_A giriş kuvvetine oranı şu şekilde elde edilir ⓘ

$$MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}},$$

ⓘ

Bu da kaldıracın mekanik avantajıdır. ⓘ

Bu denklem, dayanak noktasından giriş kuvvetinin uygulandığı A noktasına olan a mesafesinin, dayanak noktasından çıkış kuvvetinin uygulandığı B noktasına olan b mesafesinden daha büyük olması durumunda, kaldıracın giriş kuvvetini güçlendirdiğini göstermektedir. Eğer bunun tersi doğruysa, yani dayanak noktasından giriş noktası A'ya olan mesafe dayanak noktasından çıkış noktası B'ye olan mesafeden daha azsa, o zaman kaldıraç giriş kuvvetinin büyüklüğünü azaltır. ⓘ