Determinant

Matematikte determinant, bir kare matrisin girdilerinin bir fonksiyonu olan skaler bir değerdir. Matrisin ve matris tarafından temsil edilen doğrusal haritanın bazı özelliklerini karakterize etmeyi sağlar. Özellikle, determinant ancak ve ancak matris ters çevrilebilirse ve matris tarafından temsil edilen doğrusal harita bir izomorfizm ise sıfır değildir. Bir matrisler çarpımının determinantı, onların determinantlarının çarpımıdır (önceki özellik bunun bir sonucudur). Bir A matrisinin determinantı det(A), det A veya |A| olarak gösterilir. ⓘ

2 × 2 matris durumunda determinant şu şekilde tanımlanabilir

${\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}$ ⓘ

Benzer şekilde, 3 × 3 A matrisi için determinantı

${\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}$ ⓘ

Bu denklemdeki 2 × 2 matrisin her bir determinantı A matrisinin bir minörü olarak adlandırılır. Bu prosedür, Laplace açılımı olarak bilinen n × n matrisin determinantı için özyinelemeli bir tanım vermek üzere genişletilebilir. ⓘ

Determinantlar matematik boyunca ortaya çıkar. Örneğin, bir matris genellikle bir doğrusal denklem sistemindeki katsayıları temsil etmek için kullanılır ve diğer çözüm yöntemleri hesaplama açısından çok daha verimli olmasına rağmen, determinantlar bu denklemleri çözmek için kullanılabilir (Cramer kuralı). Determinantlar, kökleri özdeğerler olan bir matrisin karakteristik polinomunu tanımlamak için kullanılır. Geometride, n-boyutlu bir paralel yüzeyin işaretli n-boyutlu hacmi bir determinant ile ifade edilir. Bu, hesapta dış diferansiyel formlar ve Jacobian determinantı ile, özellikle çoklu integrallerdeki değişken değişimleri için kullanılır. ⓘ

Basit bir örnek olarak, ⓘ

2 × 2 matrisler

2 × 2 matrisin determinantı ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ "det" ile ya da matrisin etrafındaki dikey çubuklarla gösterilir ve şu şekilde tanımlanır

$\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.$

Örneğin,

$\det {\begin{pmatrix}3&7\\1&-4\end{pmatrix}}={\begin{vmatrix}3&7\\1&{-4}\end{vmatrix}}=3\cdot (-4)-7\cdot 1=-19.$ ⓘ

İlk mülkler

Determinant, aşağıdakiler için tanımın doğrudan değerlendirilmesiyle kanıtlanabilecek birkaç temel özelliğe sahiptir $2\times 2$-matrisler için geçerlidir ve daha büyük matrislerin determinantları için de geçerli olmaya devam eder. Bunlar aşağıdaki gibidir: ilk olarak, özdeşlik matrisinin determinantı ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ 1'dir. İkinci olarak, iki satır aynı ise determinant sıfırdır:

${\begin{vmatrix}a&b\\a&b\end{vmatrix}}=ab-ba=0.$

Bu durum iki sütunun aynı olması halinde de geçerlidir. Dahası,

${\begin{vmatrix}a&b+b'\\c&d+d'\end{vmatrix}}=a(d+d')-(b+b')c={\begin{vmatrix}a&b\\c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.$

Son olarak, herhangi bir sütun bir sayı ile çarpılırsa $r$ (yani, o sütundaki tüm girdiler o sayı ile çarpılır), determinant da o sayı ile çarpılır:

${\begin{vmatrix}r\cdot a&b\\r\cdot c&d\end{vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\begin{vmatrix}a&b\\c&d\end{vmatrix}}.$ ⓘ

Geometrik anlamı

Paralelkenarın alanı, paralelkenarın kenarlarını temsil eden vektörlerin oluşturduğu matrisin determinantının mutlak değeridir. ⓘ

Matris girdileri gerçek sayılar ise, A matrisi iki doğrusal eşlemeyi temsil etmek için kullanılabilir: biri standart temel vektörleri A'nın satırlarına eşleyen, diğeri ise bunları A'nın sütunlarına eşleyen. Her iki durumda da, temel vektörlerin görüntüleri, eşleme altındaki birim karenin görüntüsünü temsil eden bir paralelkenar oluşturur. Yukarıdaki matrisin satırları tarafından tanımlanan paralelkenar, ekteki diyagramda gösterildiği gibi, köşeleri (0, 0), (a, b), (a + c, b + d) ve (c, d) olan bir paralelkenardır. ⓘ

ad - bc'nin mutlak değeri paralelkenarın alanıdır ve dolayısıyla alanların A tarafından dönüştürüldüğü ölçek faktörünü temsil eder. (A'nın sütunlarının oluşturduğu paralelkenar genel olarak farklı bir paralelkenardır, ancak determinant satırlara ve sütunlara göre simetrik olduğundan, alan aynı olacaktır). ⓘ

İşaretle birlikte determinantın mutlak değeri paralelkenarın yönlendirilmiş alanı olur. Yönlendirilmiş alan normal alanla aynıdır, ancak paralelkenarı tanımlayan birinci vektörden ikinci vektöre olan açı saat yönünde döndüğünde negatif olur (bu, özdeşlik matrisi için elde edilecek yönün tersidir). ⓘ

ad - bc'nin işaretli alan olduğunu göstermek için, paralelkenarın kenarlarını temsil eden u ≡ (a, b) ve v ≡ (c, d) vektörlerini içeren bir matris düşünülebilir. İşaretli alan, vektörler arasındaki θ açısı için |u| |v| sin θ olarak ifade edilebilir, bu da basitçe taban çarpı yükseklik, bir vektörün uzunluğu çarpı diğerinin dik bileşenidir. Sinüs nedeniyle bu zaten işaretli alandır, ancak dik bir vektörün tamamlayıcı açısının kosinüsü kullanılarak daha uygun bir şekilde ifade edilebilir, örneğin u^⊥ = (-b, a), böylece |u^⊥| |v| cos θ′, skaler çarpım modeliyle ad - bc'ye eşit olduğu belirlenebilir:

${\text{Signed area}}=|{\boldsymbol {u}}|\,|{\boldsymbol {v}}|\,\sin \,\theta =\left|{\boldsymbol {u}}^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix}}\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.$ ⓘ

Bu paralel yüzeyin hacmi, r1, r2 ve r3 vektörlerinden oluşturulan sütunların oluşturduğu matrisin determinantının mutlak değeridir. ⓘ

Böylece determinant, ölçekleme faktörünü ve A tarafından temsil edilen eşleme tarafından indüklenen yönelimi verir. Determinant bire eşit olduğunda, matris tarafından tanımlanan doğrusal eşleme eşittir ve yönelimi korur. ⓘ

Bivektör olarak bilinen nesne bu fikirlerle ilişkilidir. 2B'de, her biri orijin (0, 0) ve koordinatları (a, b) ve (c, d) olan iki vektör hayal edilerek oluşturulan yönlendirilmiş bir düzlem parçası olarak yorumlanabilir. İki vektörlü büyüklük ((a, b) ∧ (c, d) ile gösterilir) işaretli alandır ve aynı zamanda ad - bc determinantıdır. ⓘ

Bir n × n reel matris A, sütun vektörleri cinsinden yazılırsa $A=\left[{\begin{array}{c|c|c|c}\mathbf {a} _{1}&\mathbf {a} _{2}&\cdots &\mathbf {a} _{n}\end{array}}\right]$, sonra

$A{\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{1},\quad A{\begin{pmatrix}0\\1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\\vdots \\1\end{pmatrix}}=\mathbf {a} _{n}.$ ⓘ

Bu şu anlama gelir $A$ birim n-küpünü, vektörler tarafından tanımlanan n-boyutlu paralelotopa eşler $\mathbf {a} _{1},\mathbf {a} _{2},\ldots ,\mathbf {a} _{n},$ bölge $P=\left\{c_{1}\mathbf {a} _{1}+\cdots +c_{n}\mathbf {a} _{n}\mid 0\leq c_{i}\leq 1\ \forall i\right\}.$ ⓘ

Determinant, bu paralelotopun işaretli n-boyutlu hacmini verir, $\det(A)=\pm {\text{vol}}(P),$ ve dolayısıyla daha genel olarak A tarafından üretilen doğrusal dönüşümün n-boyutlu hacim ölçekleme faktörünü tanımlar. (İşaret, dönüşümün yönelimi koruyup korumadığını veya tersine çevirip çevirmediğini gösterir). Özellikle, determinant sıfırsa, bu paralelotopun hacmi sıfırdır ve tam n-boyutlu değildir, bu da A'nın görüntüsünün boyutunun n'den küçük olduğunu gösterir. Bu, A'nın ne onto ne de bire-bir olan ve dolayısıyla ters çevrilebilir olmayan bir doğrusal dönüşüm ürettiği anlamına gelir. ⓘ

Tanım

Devamında, A n satırlı ve n sütunlu bir kare matristir, böylece aşağıdaki gibi yazılabilir

$A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{bmatrix}}.$ ⓘ

Girişler $a_{1,1}$ vb. birçok amaç için gerçek veya karmaşık sayılardır. Aşağıda tartışıldığı gibi, determinant, girdileri değişmeli halkalar olarak bilinen daha soyut cebirsel yapıların elemanları olan matrisler için de tanımlanır. ⓘ

A'nın determinantı det(A) ile gösterilir veya parantezler yerine çevreleyen çubuklar yazılarak doğrudan matris girdileri cinsinden gösterilebilir:

${\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}.$ ⓘ

Kare bir A matrisinin, yani aynı sayıda satır ve sütuna sahip bir matrisin determinantını tanımlamanın çeşitli eşdeğer yolları vardır: determinant, matrisin belirli girişlerinin çarpımlarının toplamlarını içeren açık bir formül olan Leibniz formülü aracılığıyla tanımlanabilir. Determinant, matrisin belirli özellikleri karşılayan girdilerine bağlı olarak benzersiz bir fonksiyon olarak da tanımlanabilir. Bu yaklaşım, söz konusu matrisleri basitleştirerek determinantları hesaplamak için de kullanılabilir. ⓘ

Leibniz formülü

3×3 matrisin determinantı için Leibniz formülü aşağıdaki gibidir:

${\begin{aligned}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a(ei-fh)-b(di-fg)+c(dh-eg)\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}$ ⓘ

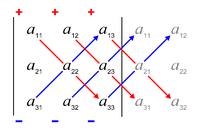
Sarrus kuralı bu formül için bir anımsatıcıdır: matrisin ilk iki sütununun kopyaları şekildeki gibi yanına yazıldığında, matris elemanlarının kuzey-batıdan güney-doğuya üç köşegen satırının çarpımlarının toplamı, eksi elemanların güney-batıdan kuzey-doğuya üç köşegen satırının çarpımlarının toplamı:

Bir 3 × 3 matrisin determinantını hesaplamak için kullanılan bu şema daha yüksek boyutlara taşınmaz. ⓘ

n × n matrisler

Leibniz formülü, bir determinantı şu şekilde ifade eder $n\times n$-matrisini daha yüksek boyutlarda tutarlı bir şekilde ifade eder. ⓘ

Permütasyon kavramını ve bunların imzasını içeren bir ifadedir. Kümenin bir permütasyonu $\{1,2,\dots ,n\}$ bir fonksiyondur $\sigma$ bu tamsayı kümesini yeniden sıralar. İçindeki değer $i$yeniden sıralamadan sonraki -inci konum $\sigma$ ile gösterilir $\sigma _{i}$. Simetrik grup olarak adlandırılan tüm bu permütasyonların kümesi şu şekilde gösterilir $S_{n}$. İmza $\sigma$ olarak tanımlanır $+1$ tarafından verilen yeniden sıralama $\sigma$ iki girdinin art arda çift sayıda değiştirilmesiyle elde edilebilir ve $-1$ tek sayıda bu tür değişimlerle elde edilebildiği zaman. ⓘ

Bir permütasyon verildiğinde $\sigma$ ve bir $n\times n$-matris $A$, nerede $a_{i,j}$ 'deki elemanı belirtir. $i$-inci sıra ve $j$'nin -'inci sütunu $A$, ürün

$a_{1,\sigma _{1}}\cdot a_{2,\sigma _{2}}\cdot \dots \cdot a_{n,\sigma _{n}}$,

Pi notasyonu kullanılarak daha kısaca şu şekilde de yazılabilir

$\prod _{i=1}^{n}a_{i,\sigma _{i}}$,

Leibniz formülünü kullanarak determinantı tanımlamak için kullanılır:

$\det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}\right)$. ⓘ

Aşağıdaki tablo bu terimleri şu durumda çözmektedir $n=3$. İlk sütunda, bir permütasyon değerlerine göre listelenir. Örneğin, ikinci satırda, permütasyon $\sigma$ tatmin eder $\sigma _{1}=1,\sigma _{2}=3,\sigma _{3}=2$. Standart sıralamadan (1, 2, 3) tek bir değişimle (ikinci ve üçüncü girdiyi değiştirerek) elde edilebilir, böylece imzası $\operatorname {sgn}(\sigma )=-1$. ⓘ

Permütasyonları $\{1,2,3\}$ ve bunların determinantlara katkısı ⓘ

Permütasyon $\sigma$	$\operatorname {sgn}(\sigma )$	$\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}$
1, 2, 3	$+1$	$+a_{1,1}a_{2,2}a_{3,3}$
1, 3, 2	$-1$	$-a_{1,1}a_{2,3}a_{3,2}$
3, 1, 2	$+1$	$+a_{1,3}a_{2,1}a_{3,2}$
3, 2, 1	$-1$	$-a_{1,3}a_{2,2}a_{3,1}$
2, 3, 1	$+1$	$+a_{1,2}a_{2,3}a_{3,1}$
2, 1, 3	$-1$	$-a_{1,2}a_{2,1}a_{3,3}$

Üçüncü sütundaki altı terimin toplamı şu şekildedir ⓘ

$\sum _{\sigma \in S_{3}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}=a_{1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}+a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}+a_{1,2}a_{2,3}a_{3,1}-a_{1,2}a_{2,1}a_{3,3}.$

Bu, aşağıdakiler için formülü geri verir $3\times 3$-matrisler yukarıda. Genel bir matris için $n\times n$-matrisi için Leibniz formülü şunları içerir $n!$ Her biri matrisin n girişinin çarpımı olan (n faktöriyel) toplamlar. ⓘ

Leibniz formülü, sadece permütasyonların değil, aynı zamanda tüm dizilerin bir toplamı kullanılarak da ifade edilebilir. $n$ aralığındaki endeksler $1,\dots ,n$ meydana gelir. Bunu yapmak için Levi-Civita sembolü kullanılır $\varepsilon _{i_{1},\cdots ,i_{n}}$ bir permütasyonun işareti yerine

$\det(A)=\sum _{i_{1},i_{2},\ldots ,i_{n}=1}^{n}\varepsilon _{i_{1}\cdots i_{n}}a_{1,i_{1}}\cdots a_{n,i_{n}},$

Bu, yukarıdaki formülü geri verir, çünkü Levi-Civita sembolü, eğer indisler $i_{1},\dots ,i_{n}$ bir permütasyon oluşturmaz. ⓘ

Determinantın özellikleri

Determinantın karakterizasyonu

Determinant aşağıdaki üç temel özellik ile karakterize edilebilir. Bunları belirtmek için, bir $n\times n$-A matrisinin kendi matrisinden oluşması $n$ sütunlar, yani şu şekilde gösterilir

$A={\big (}a_{1},\dots ,a_{n}{\big )},$

burada sütun vektörü $a_{i}$ (her i için) i'inci sütundaki matrisin girdilerinden oluşur. ⓘ

2. $\det \left(I\right)=1$, nerede $I$ bir kimlik matrisidir.
4. Determinant çoklu doğrusaldır: eğer bir matrisin j. sütunu $A$ doğrusal bir kombinasyon olarak yazılır $a_{j}=r\cdot v+w$ v ve w sütun vektörlerinden ve bir r sayısından oluşuyorsa, A'nın determinantı benzer bir doğrusal kombinasyon olarak ifade edilebilir:

   ${\begin{aligned}|A|&={\big |}a_{1},\dots ,a_{j-1},r\cdot v+w,a_{j+1},\dots ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n}|\end{aligned}}$

6. Determinant dönüşümlüdür: bir matrisin iki sütunu aynı olduğunda, determinantı 0'dır:

   $|a_{1},\dots ,v,\dots ,v,\dots ,a_{n}|=0.$ ⓘ

Determinant yukarıdaki gibi Leibniz formülü kullanılarak tanımlanırsa, bu üç özellik formülün doğrudan incelenmesiyle kanıtlanabilir. Bazı yazarlar da determinantı doğrudan bu üç özelliği kullanarak ele alırlar: herhangi bir matrise atanan tam olarak bir fonksiyon olduğu gösterilebilir. $n\times n$-A matrisi bu üç özelliği karşılayan bir sayıdır. Bu aynı zamanda determinanta bu daha soyut yaklaşımın Leibniz formülünü kullanan tanımla aynı tanımı verdiğini gösterir. ⓘ

Bunu görmek için determinantı sütunlardaki çoklu doğrusallıkla genişleterek, her sütunun standart bir temel vektör olduğu matrislerin determinantlarının (büyük) bir doğrusal kombinasyonuna dönüştürmek yeterlidir. Bu determinantlar ya 0 (özellik 9'a göre) ya da ±1'dir (aşağıdaki özellik 1 ve 12'ye göre), dolayısıyla doğrusal kombinasyon Levi-Civita sembolü cinsinden yukarıdaki ifadeyi verir. Görünüşte daha az teknik olsa da, bu tanımlama determinantı tanımlamada Leibniz formülünün yerini tamamen alamaz, çünkü bu formül olmadan uygun bir fonksiyonun varlığı açık değildir. ⓘ

Anlık sonuçlar

Bu kuralların birkaç başka sonucu daha vardır:

• Determinant homojen bir fonksiyondur, yani,
  $$\det(cA)=c^{n}\det(A)$$
  (bir $n\times n$ matris $A$).
• Bir matrisin herhangi bir sütun çiftinin yer değiştirmesi, matrisin determinantını -1 ile çarpar. Bu, determinantın çok doğrusal ve dönüşümlü olmasından kaynaklanır (yukarıdaki 2. ve 3. özellikler):
  $$|a_{1},\dots ,a_{j},\dots a_{i},\dots ,a_{n}|=-|a_{1},\dots ,a_{i},\dots ,a_{j},\dots ,a_{n}|.$$
  Bu formül, birkaç sütun yer değiştirdiğinde iteratif olarak uygulanabilir. Örneğin
  $$|a_{3},a_{1},a_{2},a_{4}\dots ,a_{n}|=-|a_{1},a_{3},a_{2},a_{4},\dots ,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\dots ,a_{n}|.$$
  Ancak daha genel olarak, sütunların herhangi bir permütasyonu determinantı permütasyonun işareti ile çarpar.
• Eğer bir sütun diğer sütunların doğrusal kombinasyonu olarak ifade edilebiliyorsa (yani matrisin sütunları doğrusal olarak bağımlı bir küme oluşturuyorsa), determinant 0'dır. Özel bir durum olarak, buna şunlar dahildir: eğer bir sütun tüm girdileri sıfır olacak şekildeyse, o zaman bu matrisin determinantı 0'dır.
• Bir sütunun skaler bir katını başka bir sütuna eklemek determinantın değerini değiştirmez. Bu, çoklu doğrusallığın ve alternatif olmanın bir sonucudur: çoklu doğrusallık ile determinant, iki eşit sütunlu bir matrisin determinantının bir katı ile değişir, determinant alternatif olduğu için determinant 0'dır.
• Eğer $A$ üçgen bir matristir, yani $a_{ij}=0$, her ne zaman $i>j$ veya alternatif olarak, her ne zaman $i<j$o zaman matrisin determinantı köşegen girdilerin çarpımına eşittir:
  $$\det(A)=a_{11}a_{22}\cdots a_{nn}=\prod _{i=1}^{n}a_{ii}.$$
  Aslında, böyle bir matris, daha az sıfırsız girdisi olan sütunların katlarını daha fazla girdisi olanlara uygun şekilde ekleyerek (determinantı değiştirmeden) bir köşegen matrise indirgenebilir. Böyle bir matris için, her sütundaki doğrusallığı kullanmak özdeşlik matrisine indirger, bu durumda belirtilen formül determinantların ilk karakterize edici özelliği ile geçerlidir. Alternatif olarak, bu formül Leibniz formülünden de çıkarılabilir, çünkü tek permütasyon $\sigma$ sıfır olmayan bir katkı sağlayan permütasyon özdeşlik permütasyonudur. ⓘ

Örnek

Yukarıda listelenen bu karakterize edici özellikler ve sonuçları hem teorik olarak önemlidir, hem de somut matrisler için determinantları hesaplamak için kullanılabilir. Aslında, Gauss eliminasyonu herhangi bir matrisi üst üçgen formuna getirmek için uygulanabilir ve bu algoritmadaki adımlar determinantı kontrollü bir şekilde etkiler. Aşağıdaki somut örnek, matrisin determinantının hesaplanmasını göstermektedir $A$ bu yöntemi kullanarak:

$A={\begin{bmatrix}-2&-1&2\\2&1&4\\-3&3&-1\end{bmatrix}}.$ ⓘ

Matrisin determinantının hesaplanması $A$ ⓘ

Matris	$B={\begin{bmatrix}-3&-1&2\\3&1&4\\0&3&-1\end{bmatrix}}$	$C={\begin{bmatrix}-3&5&2\\3&13&4\\0&0&-1\end{bmatrix}}$	$D={\begin{bmatrix}5&-3&2\\13&3&4\\0&0&-1\end{bmatrix}}$	$E={\begin{bmatrix}18&-3&2\\0&3&4\\0&0&-1\end{bmatrix}}$
Tarafından elde edildi	ikinci sütunu birinciye ekleyin	üçüncü sütunun 3 katını ikinciye ekleyin	ilk iki sütunu değiştirin	ekle $-{\frac {13}{3}}$ ikinci sütunu birinciyle çarpın
Belirleyici	$|A|=|B|$	$|B|=|C|$	$|D|=-|C|$	$|E|=|D|$

Bu eşitlikler birleştirildiğinde $|A|=-|E|=-(18\cdot 3\cdot (-1))=54.$ ⓘ

Transpoze

'nin transpozesinin determinantıdır. $A$ A'nın determinantına eşittir:

$\det \left(A^{\textsf {T}}\right)=\det(A)$.

Bu, Leibniz formülü incelenerek kanıtlanabilir. Bu, yukarıda bahsedilen tüm özelliklerde "sütun" kelimesinin "satır" ile değiştirilebileceği anlamına gelir. Örneğin, bir n × n matrisin n satırdan oluştuğu düşünülürse, determinant n-lineer bir fonksiyondur. ⓘ

Çarpımsallık ve matris grupları

Dolayısıyla determinant çarpımsal bir haritadır, yani kare matrisler için $A$ ve $B$ eşit büyüklükte ise, bir matris çarpımının determinantı bunların determinantlarının çarpımına eşittir:

$\det(AB)=\det(A)\det(B)$ ⓘ

Bu önemli gerçek, sabit bir matris için şu gözlemle kanıtlanabilir $B$'nin sütunlarına bağlı bir fonksiyon olarak denklemin her iki tarafı da dönüşümlü ve çok doğrusaldır. $A$. Dahası, her ikisi de $\det B$ ne zaman $A$ özdeşlik matrisidir. Alternatif çoklu doğrusal haritaların yukarıda bahsedilen benzersiz karakterizasyonu bu iddiayı göstermektedir. ⓘ

Bir matris $A$ determinantı sıfır değilse tam olarak ters çevrilebilirdir. Bu, çarpımsallığından kaynaklanır. $\det$ ve aşağıda belirtilen eşlenik matrisi içeren tersin formülü. Bu durumda, ters matrisin determinantı şu şekilde verilir

$\det \left(A^{-1}\right)={\frac {1}{\det(A)}}=[\det(A)]^{-1}$. ⓘ

Özellikle, determinantı sıfır olmayan (sırasıyla determinantı bir olan) matrislerin çarpımları ve tersleri hala bu özelliğe sahiptir. Dolayısıyla, bu tür matrislerin kümesi (sabit boyutlu $n$) genel doğrusal grup olarak bilinen bir grup oluşturur $\operatorname {GL} _{n}$ (sırasıyla, özel doğrusal grup olarak adlandırılan bir alt grup $\operatorname {SL} _{n}\subset \operatorname {GL} _{n}$. Daha genel olarak, "özel" kelimesi determinantı bir olan matrislerden oluşan başka bir matris grubunun alt grubunu belirtir. Örnekler arasında özel ortogonal grup (n 2 veya 3 ise tüm rotasyon matrislerinden oluşur) ve özel üniter grup yer alır. ⓘ

Cauchy-Binet formülü, dikdörtgen matrisler için bu çarpım formülünün bir genellemesidir. Bu formül, girdileri belirli bir matrisin tüm ikinci dereceden alt matrislerinin determinantları olan bileşik matrisler için çarpımsal bir formül olarak da yeniden oluşturulabilir. ⓘ

Laplace açılımı

Laplace açılımı bir matrisin determinantını ifade eder $A$ minörleri olarak bilinen daha küçük matrislerin determinantları cinsinden ifade edilebilir. Minör $M_{i,j}$ 'nin determinantı olarak tanımlanır. $(n-1)\times (n-1)$'den kaynaklanan -matris $A$ kaldırarak $i$-inci sıra ve $j$-inci sütun. İfade $(-1)^{i+j}M_{i,j}$ kofaktör olarak bilinir. Her bir kofaktör için $i$eşitliğine sahiptir.

$\det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}M_{ij},$

Bu, birinci satır boyunca Laplace açılımı olarak adlandırılır. Örneğin, ilk satır boyunca Laplace açılımı ($i=1$) aşağıdaki formülü verir:

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}$

Bu determinantların çözülmesi $2\times 2$-matrisleri yukarıda bahsedilen Leibniz formülünü geri verir. Benzer şekilde, Laplace açılımı $j$-inci sütun eşitliktir

$\det(A)=\sum _{i=1}^{n}(-1)^{i+j}a_{ij}M_{ij}.$

Laplace açılımı determinantları hesaplamak için iteratif olarak kullanılabilir, ancak bu yaklaşım büyük matrisler için verimsizdir. Bununla birlikte, Vandermonde matrisi gibi yüksek simetrik matrislerin determinantlarını hesaplamak için kullanışlıdır

$${\begin{vmatrix}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{vmatrix}}=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).$$

Bu determinant, örneğin, transandantal sayılar teorisinde Baker teoreminin ispatında uygulanmıştır. ⓘ

Eşlenik matris

Eşlenik matris $\operatorname {adj} (A)$ kofaktörler matrisinin transpozesidir, yani,

$(\operatorname {adj} (A))_{ij}=(-1)^{i+j}M_{ji}.$ ⓘ

Her matris için bir tane vardır

$(\det A)I=A\operatorname {adj} A=(\operatorname {adj} A)\,A.$ ⓘ

Böylece eşlenik matris, tekil olmayan bir matrisin tersini ifade etmek için kullanılabilir:

$A^{-1}={\frac {1}{\det A}}\operatorname {adj} A.$ ⓘ

Blok matrisler

a'nın determinantı için formül $2\times 2$-matrisi, uygun ek varsayımlar altında, bir blok matris, yani dört alt matristen oluşan bir matris için geçerli olmaya devam eder $A,B,C,D$ boyutun $n\times n$, $n\times m$, $m\times n$ ve $m\times m$sırasıyla. Leibniz formülü ya da Schur tümleyenini içeren bir çarpanlara ayırma kullanılarak kanıtlanabilen bu tür en kolay formül

$\det {\begin{pmatrix}A&0\\C&D\end{pmatrix}}=\det(A)\det(D)=\det {\begin{pmatrix}A&B\\0&D\end{pmatrix}}.$

Eğer $A$ ters çevrilebilir (ve benzer şekilde eğer $D$ ters çevrilebilir), biri vardır ⓘ

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(A)\det \left(D-CA^{-1}B\right).$

Eğer $D$ bir $1\times 1$-matrisi için bu durum şu şekilde basitleşir $\det(A)(D-CA^{-1}B)$. ⓘ

Bloklar aynı boyutta kare matrisler ise başka formüller de geçerlidir. Örneğin, eğer $C$ ve $D$ (yani, $CD=DC$), o zaman vardır ⓘ

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).$

Bu formül, birden fazla matristen oluşan matrisler için genelleştirilmiştir. $2\times 2$ bloklar, yine her bir blok arasında uygun değişebilirlik koşulları altında. ⓘ

İçin $A=D$ ve $B=C$aşağıdaki formül geçerlidir (aşağıdaki durumlarda bile $A$ ve $B$ işe gidip gelmeyin)

$\det {\begin{pmatrix}A&B\\B&A\end{pmatrix}}=\det(A-B)\det(A+B).$ ⓘ

Sylvester'ın determinant teoremi

Sylvester'ın determinant teoremi, bir m × n matris olan A ve bir n × m matris olan B için (böylece A ve B, bir kare matris oluşturan her iki sırada da çarpılmalarına izin veren boyutlara sahiptir):

$\det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),$ ⓘ

Burada Im ve In sırasıyla m × m ve n × n özdeşlik matrisleridir. ⓘ

Bu genel sonuçtan birkaç sonuç çıkar.

1. Her biri m bileşenli c sütun vektörü ve r satır vektörü için formül, özdeşlik matrisinden rankı 1 olan bir matrisle farklı olan bir matrisin determinantının hızlı bir şekilde hesaplanmasını sağlar:

   $\det \left(I_{\mathit {m}}+cr\right)=1+rc.$

2. Daha genel olarak, herhangi bir ters çevrilebilir m × m matris X için,
   $\det(X+AB)=\det(X)\det \left(I_{\mathit {n}}+BX^{-1}A\right),$
3. Yukarıdaki gibi bir sütun ve satır vektörü için:
   $\det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right)=\det(X)+r\,\operatorname {adj} (X)\,c.$
4. Kare matrisler için $A$ ve $B$ aynı boyutta, matrisler $AB$ ve $BA$ aynı karakteristik polinomlara (dolayısıyla aynı özdeğerlere) sahiptir. ⓘ

Toplam

Toplamın determinantı $A+B$ aynı boyuttaki iki kare matrisin A ve B'nin determinantları cinsinden genel olarak ifade edilemez. Ancak, pozitif yarı sonsuz matrisler için $A$, $B$ ve $C$ eşit büyüklükte,

$$\det(A+B+C)+\det(C)\geq \det(A+C)+\det(B+C){\text{,}}$$

sonuç ile

$$\det(A+B)\geq \det(A)+\det(B){\text{.}}$$

Tersine, eğer $A$ ve $B$ Hermitian, pozitif tanımlı ve büyüklük $n\times n$, o zaman determinant içbükey $n$inci kök; bu şu anlama gelir

$${\sqrt[{n}]{\det {\!(A+B)}}}\leq {\sqrt[{n}]{\det {\!(A)}}}+{\sqrt[{n}]{\det {\!(B)}}}$$

homojenlik ile. ⓘ

2×2 matrisler için toplam özdeşliği

Özel durum için $2\times 2$ Karmaşık girişli matrislerde, toplamın determinantı aşağıdaki özdeşlikte determinantlar ve izler cinsinden yazılabilir:

$\det(A+B)=\det(A)+\det(B)+{\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$ ⓘ

Özdeşliğin kanıtı

Bu, her bir terimi bileşenler halinde yazarak gösterilebilir $A_{ij},B_{ij}$. Sol taraf ise

$(A_{11}+B_{11})(A_{22}+B_{22})-(A_{12}+B_{12})(A_{21}+B_{21}).$

Genişleme sağlar

$A_{11}A_{22}+B_{11}A_{22}+A_{11}B_{22}+B_{11}B_{22}-A_{12}A_{21}-B_{12}A_{21}-A_{12}B_{21}-B_{12}B_{21}.$

'de ikinci dereceden olan terimler $A$ olduğu görülüyor $\det(A)$ve benzer şekilde $B$Bu nedenle ifade şöyle yazılabilir

$\det(A)+\det(B)+A_{11}B_{22}+B_{11}A_{22}-A_{12}B_{21}-B_{12}A_{21}.$

Daha sonra çapraz terimleri şu şekilde yazabiliriz

$(A_{11}+A_{22})(B_{11}+B_{22})-(A_{11}B_{11}+A_{12}B_{21}+A_{21}B_{12}+A_{22}B_{22})$

olarak tanınabilen

${\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$

Bu da kanıtı tamamlar. ⓘ

Bu, aşağıdakiler için bir uygulamaya sahiptir $2\times 2$ matris cebirleri. Örneğin, karmaşık sayıları bir matris cebiri olarak düşünün. Karmaşık sayıların matrisler şeklinde bir gösterimi vardır

$$aI+b\mathbf {i} :=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$$

ile $a$ ve $b$ Gerçek. O zamandan beri ${\text{tr}}(\mathbf {i} )=0$, alarak $A=aI$ ve $B=b\mathbf {i}$ Yukarıdaki özdeşlikte

$\det(aI+b\mathbf {i} )=a^{2}\det(I)+b^{2}\det(\mathbf {i} )=a^{2}+b^{2}.$

Bu sonuç, sadece ${\text{tr}}(\mathbf {i} )=0$ ve $\det(I)=\det(\mathbf {i} )=1$. ⓘ

Diğer kavramlarla ilişkili olarak determinantın özellikleri

Özdeğerler ve karakteristik polinom

Determinant, lineer cebirdeki diğer iki merkezi kavram olan özdeğerler ve bir matrisin karakteristik polinomu ile yakından ilişkilidir. İzin verin $A$ bir $n\times n$-özdeğerlere sahip karmaşık girdileri olan matris $\lambda _{1},\lambda _{2},\ldots ,\lambda _{n}$. (Burada cebirsel çokluğu μ olan bir özdeğerin bu listede μ kez yer aldığı anlaşılmaktadır). O halde A'nın determinantı tüm özdeğerlerin çarpımıdır,

$\det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.$

Sıfır olmayan tüm özdeğerlerin çarpımı sözde belirleyici olarak adlandırılır. ⓘ

Karakteristik polinom şu şekilde tanımlanır

$\chi _{A}(t)=\det(t\cdot I-A).$

İşte, $t$ polinomun belirsizliğidir ve $I$ ile aynı boyuttaki özdeşlik matrisidir. $A$. Bu polinom aracılığıyla, matrisin öz değerlerini bulmak için determinantlar kullanılabilir $A$: bunlar tam olarak bu polinomun kökleridir, yani şu karmaşık sayılardır $\lambda$ öyle ki

$\chi _{A}(\lambda )=0.$ ⓘ

Bir Hermitian matris, tüm özdeğerleri pozitif ise pozitif tanımlıdır. Sylvester'ın kriteri, bunun alt matrislerin determinantlarına eşdeğer olduğunu ileri sürer

$A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,k}\\a_{2,1}&a_{2,2}&\cdots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\cdots &a_{k,k}\end{bmatrix}}$ ⓘ

pozitif olmak üzere, tüm $k$ arasında $1$ ve $n$. ⓘ

İz

Trace tr(A) tanımı gereği A'nın köşegen girişlerinin toplamıdır ve aynı zamanda özdeğerlerin toplamına eşittir. Böylece, karmaşık matrisler için A,

$\det(\exp(A))=\exp(\operatorname {tr} (A))$ ⓘ

veya gerçek matrisler için A,

$\operatorname {tr} (A)=\log(\det(\exp(A))).$ ⓘ

Burada exp(A) A'nın matris üstelini gösterir, çünkü A'nın her λ özdeğeri exp(A)'nın exp(λ) özdeğerine karşılık gelir. Özellikle, A'nın herhangi bir logaritması, yani aşağıdaki koşulları sağlayan herhangi bir L matrisi verildiğinde

$\exp(L)=A$ ⓘ

A'nın determinantı şu şekilde verilir

$\det(A)=\exp(\operatorname {tr} (L)).$ ⓘ

Örneğin, sırasıyla n = 2, n = 3 ve n = 4 için,

${\begin{aligned}\det(A)&={\frac {1}{2}}\left(\left(\operatorname {tr} (A)\right)^{2}-\operatorname {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A)\right)^{3}-3\operatorname {tr} (A)~\operatorname {tr} \left(A^{2}\right)+2\operatorname {tr} \left(A^{3}\right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2}\right)\right)^{2}+8\operatorname {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^{4}\right)\right).\end{aligned}}$ ⓘ

Cayley-Hamilton teoremine bakınız. Bu tür ifadeler kombinatoryal argümanlardan, Newton özdeşliklerinden veya Faddeev-LeVerrier algoritmasından çıkarılabilir. Yani, genel n için, detA = (-1)nc₀ karakteristik polinomun işaretli sabit terimi, özyinelemeli olarak

$c_{n}=1;~~~c_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}c_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.$ ⓘ

Genel durumda, bu aynı zamanda aşağıdakilerden de elde edilebilir

$\det(A)=\sum _{\begin{array}{c}k_{1},k_{2},\ldots ,k_{n}\geq 0\\k_{1}+2k_{2}+\cdots +nk_{n}=n\end{array}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},$ ⓘ

Burada toplam, denklemi sağlayan tüm kl ≥ 0 tamsayılarının kümesi üzerinden alınır

$\sum _{l=1}^{n}lk_{l}=n.$ ⓘ

Formül, n argümanlı tam üstel Bell polinomu cinsinden sl = -(l - 1)! tr(Al) olarak ifade edilebilir

$\det(A)={\frac {(-1)^{n}}{n!}}B_{n}(s_{1},s_{2},\ldots ,s_{n}).$ ⓘ

Bu formül aynı zamanda çok boyutlu indisleri ^I = (i₁, i₂, ..., ir) ve _J = (j₁, j₂, ..., jr) olan bir AIJ matrisinin determinantını bulmak için de kullanılabilir. Bu tür matrislerin çarpımı ve izi doğal bir şekilde aşağıdaki gibi tanımlanır

$(AB)_{J}^{I}=\sum _{K}A_{K}^{I}B_{J}^{K},\operatorname {tr} (A)=\sum _{I}A_{I}^{I}.$ ⓘ

Genişleme yakınsadığında logaritmanın Mercator serisi genişlemesinden önemli bir keyfi boyut n özdeşliği elde edilebilir. Eğer A'nın her özdeğeri mutlak değer olarak 1'den küçükse,

$\det(I+A)=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$ ⓘ

burada I kimlik matrisidir. Daha genel olarak, eğer

$\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$ ⓘ

s'de biçimsel bir kuvvet serisi olarak genişletilirse, ^m > n için sm'nin tüm katsayıları sıfırdır ve kalan polinom det(I + sA)'dır. ⓘ

Üst ve alt sınırlar

Pozitif tanımlı bir A matrisi için, iz operatörü log determinantı üzerinde aşağıdaki sıkı alt ve üst sınırları verir

$\operatorname {tr} \left(I-A^{-1}\right)\leq \log \det(A)\leq \operatorname {tr} (A-I)$ ⓘ

Bu ilişki, iki çok değişkenli normal dağılım arasındaki KL-ıraksaması formülü aracılığıyla türetilebilir. ⓘ

Ayrıca,

${\frac {n}{\operatorname {tr} \left(A^{-1}\right)}}\leq \det(A)^{\frac {1}{n}}\leq {\frac {1}{n}}\operatorname {tr} (A)\leq {\sqrt {{\frac {1}{n}}\operatorname {tr} \left(A^{2}\right)}}.$ ⓘ

Bu eşitsizlikler, izleri ve determinantı özdeğerler cinsinden ifade ederek kanıtlanabilir. Bu nedenle, harmonik ortalamanın geometrik ortalamadan, onun da aritmetik ortalamadan, onun da kök ortalama kareden küçük olduğu şeklindeki iyi bilinen gerçeği temsil ederler. ⓘ

Türev

Leibniz formülü, gerçek (veya karmaşık matrisler için benzer şekilde) kare matrislerin determinantının aşağıdakilerden bir polinom fonksiyonu olduğunu gösterir $\mathbf {R} ^{n\times n}$ için $\mathbf {R}$. Özellikle, her yerde türevlenebilirdir. Türevi Jacobi'nin formülü kullanılarak ifade edilebilir:

${\frac {d\det(A)}{d\alpha }}=\operatorname {tr} \left(\operatorname {adj} (A){\frac {dA}{d\alpha }}\right).$ ⓘ

burada $\operatorname {adj} (A)$ 'nin eşleniğini gösterir. $A$. Özellikle, eğer $A$ ters çevrilebilir ise ⓘ

${\frac {d\det(A)}{d\alpha }}=\det(A)\operatorname {tr} \left(A^{-1}{\frac {dA}{d\alpha }}\right).$ ⓘ

'nin girişleri cinsinden ifade edilir. $A$bunlar ⓘ

${\frac {\partial \det(A)}{\partial A_{ij}}}=\operatorname {adj} (A)_{ji}=\det(A)\left(A^{-1}\right)_{ji}.$ ⓘ

Bir başka eşdeğer formülasyon da şöyledir ⓘ

$\det(A+\epsilon X)-\det(A)=\operatorname {tr} (\operatorname {adj} (A)X)\epsilon +O\left(\epsilon ^{2}\right)=\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)$, ⓘ

büyük O notasyonunu kullanarak. Özel durum nerede $A=I$, özdeşlik matrisi, şunları verir ⓘ

$\det(I+\epsilon X)=1+\operatorname {tr} (X)\epsilon +O\left(\epsilon ^{2}\right).$ ⓘ

Bu özdeşlik, belirli matris Lie gruplarıyla ilişkili Lie cebirlerini tanımlamada kullanılır. Örneğin, özel lineer grup $\operatorname {SL} _{n}$ denklemi ile tanımlanır $\det A=1$. Yukarıdaki formül, Lie cebirinin özel lineer Lie cebiri olduğunu göstermektedir ${\mathfrak {sl}}_{n}$ izi sıfır olan matrislerden oluşur. ⓘ

Yazma a $3\times 3$-matris olarak $A={\begin{bmatrix}a&b&c\end{bmatrix}}$ burada $a,b,c$ uzunlukları 3 olan sütun vektörler ise, üç vektörden biri üzerindeki gradyan diğer ikisinin çapraz çarpımı olarak yazılabilir:

${\begin{aligned}\nabla _{\mathbf {a} }\det(A)&=\mathbf {b} \times \mathbf {c} \\\nabla _{\mathbf {b} }\det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\end{aligned}}$ ⓘ

Tarih

Tarihsel olarak, determinantlar matrislerden çok daha önce kullanılmıştır: Bir determinant başlangıçta bir doğrusal denklem sisteminin bir özelliği olarak tanımlanmıştır. Determinant, sistemin benzersiz bir çözümü olup olmadığını "belirler" (determinant sıfır değilse bu tam olarak gerçekleşir). Bu anlamda determinantlar ilk olarak Çin matematiği ders kitabı Matematik Sanatı Üzerine Dokuz Bölüm'de (九章算術, Çinli bilginler, M.Ö. 3. yüzyıl civarında) kullanılmıştır. Avrupa'da, iki denklemli doğrusal sistemlerin çözümleri 1545 yılında Cardano tarafından determinant benzeri bir varlık ile ifade edilmiştir. ⓘ

Determinantlar Japonya'da 1683'te Seki Takakazu'nun ve paralel olarak 1693'te Leibniz'in çalışmalarından kaynaklanmıştır. Cramer (1750) kanıt olmaksızın Cramer kuralını ifade etmiştir. Hem Cramer hem de Bezout (1779), belirli bir nokta kümesinden geçen düzlem eğrileri sorusuyla determinantlara yönlendirildi. ⓘ

Vandermonde (1771) determinantları ilk olarak bağımsız fonksiyonlar olarak kabul etti. Laplace (1772) bir determinantı tamamlayıcı minörleri cinsinden genişletmenin genel yöntemini verdi: Vandermonde zaten özel bir durum vermişti. Hemen ardından Lagrange (1773) ikinci ve üçüncü dereceden determinantları ele aldı ve bunu eleme teorisi sorularına uyguladı; genel özdeşliklerin birçok özel durumunu kanıtladı. ⓘ

Bir sonraki ilerlemeyi Gauss (1801) yaptı. Lagrange gibi o da sayılar teorisinde determinantlardan çokça yararlandı. "Determinant" sözcüğünü ortaya attı (Laplace "sonuç" sözcüğünü kullanmıştı), ancak bugünkü anlamıyla değil, daha ziyade bir kuantiğin diskriminantına uygulandığı şekliyle. Gauss ayrıca karşılıklı (ters) determinantlar kavramına ulaştı ve çarpma teoremine çok yaklaştı. ⓘ

Bir sonraki önemli katkı, m sütunlu ve n satırlı iki matrisin çarpımına ilişkin teoremi resmi olarak ifade eden ve m = n özel durumu için çarpma teoremine indirgeyen Binet'dir (1811, 1812). Binet'nin Akademi'ye bildirisini sunduğu aynı gün (30 Kasım 1812) Cauchy de konuyla ilgili bir bildiri sundu. (Bkz. Cauchy-Binet formülü.) Bu bildiride "determinant" sözcüğünü bugünkü anlamıyla kullandı, o zamanlar bu konuda bilinenleri özetledi ve basitleştirdi, notasyonu geliştirdi ve çarpma teoremini Binet'ninkinden daha tatmin edici bir kanıtla verdi. Teorinin genelliği onunla başlar. ⓘ

(Jacobi 1841) Sylvester'ın daha sonra Jacobian olarak adlandırdığı fonksiyonel determinantı kullandı. Crelle's Journal for 1841'deki anılarında bu konuyu ve Sylvester'in alternant olarak adlandırdığı alternatif fonksiyonlar sınıfını özel olarak ele alır. Jacobi'nin son anıları sırasında Sylvester (1839) ve Cayley çalışmalarına başladılar. Cayley 1841'de dikey çubuklar kullanarak determinant için modern notasyonu tanıttı. ⓘ

Determinantların özel formlarının incelenmesi, genel teorinin tamamlanmasının doğal bir sonucu olmuştur. Eksen simetrik determinantlar Lebesgue, Hesse ve Sylvester tarafından; persimetrik determinantlar Sylvester ve Hankel tarafından; sirkülantlar Catalan, Spottiswoode, Glaisher ve Scott tarafından; çarpık determinantlar ve Pfaffianlar, ortogonal dönüşüm teorisi ile bağlantılı olarak Cayley tarafından çalışılmıştır; Sylvester tarafından sürekli determinantlar; Christoffel ve Frobenius tarafından Wronskians (Muir tarafından böyle adlandırılmıştır); Sylvester, Reiss ve Picquet tarafından bileşik determinantlar; Sylvester tarafından Jacobians ve Hessians; ve Trudi tarafından simetrik gauche determinantları. Konuyla ilgili ders kitapları arasında Spottiswoode'unki ilktir. Amerika'da Hanus (1886), Weld (1893) ve Muir/Metzler (1933) incelemeler yayınlamıştır. ⓘ

Uygulamalar

Cramer'in kuralı

Determinantlar, matris formunda aşağıdaki gibi yazılan doğrusal bir denklem sisteminin çözümlerini tanımlamak için kullanılabilir $Ax=b$. Bu denklemin tek bir çözümü vardır $x$ eğer ve sadece $\det(A)$ sıfır değildir. Bu durumda çözüm Cramer kuralı ile verilir:

$x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,2,3,\ldots ,n$ ⓘ

burada $A_{i}$ yerine konulmasıyla oluşturulan matristir. $i$'nin -'inci sütunu $A$ sütun vektörü tarafından $b$. Bu, determinantın sütun açılımı ile hemen takip edilir, yani

$\det(A_{i})=\det {\begin{bmatrix}a_{1}&\ldots &b&\ldots &a_{n}\end{bmatrix}}=\sum _{j=1}^{n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix}}=x_{i}\det(A)$

burada vektörler $a_{j}$ A'nın sütunlarıdır. Bu kural aynı zamanda şu özdeşlik tarafından da ima edilir ⓘ

$A\,\operatorname {adj} (A)=\operatorname {adj} (A)\,A=\det(A)\,I_{n}.$ ⓘ

Cramer'in kuralı şu şekilde uygulanabilir $\operatorname {O} (n^{3})$ LU, QR veya tekil değer ayrıştırması gibi doğrusal denklem sistemlerini çözmenin daha yaygın yöntemleriyle karşılaştırılabilir. ⓘ

Doğrusal bağımsızlık

Determinantlar doğrusal olarak bağımlı vektörleri karakterize etmek için kullanılabilir: $\det A$ matrisinin sütun vektörleri (veya eşdeğer olarak satır vektörleri) sıfır ise ve sadece $A$ doğrusal olarak bağımlıdır. Örneğin, doğrusal olarak bağımsız iki vektör verildiğinde $v_{1},v_{2}\in \mathbf {R} ^{3}$, üçüncü bir vektör $v_{3}$ 'nin determinantı tam olarak önceki iki vektör tarafından yayılan düzlemde yer alıyorsa $3\times 3$-Üç vektörden oluşan matris sıfırdır. Aynı fikir diferansiyel denklemler teorisinde de kullanılır: verilen fonksiyonlar $f_{1}(x),\dots ,f_{n}(x)$ (olması gerekiyordu $n-1$ kez türevlenebilir), Wronskian şu şekilde tanımlanır

$W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.$ ⓘ

Sıfır değildir (bazı $x$) belirli bir aralıkta ancak ve ancak verilen fonksiyonlar ve bunların mertebeye kadar tüm türevleri $n-1$ doğrusal olarak bağımsızdır. Wronskian'ın bir aralık üzerinde her yerde sıfır olduğu gösterilebilirse, analitik fonksiyonlar söz konusu olduğunda, bu, verilen fonksiyonların doğrusal olarak bağımlı olduğu anlamına gelir. Wronskian ve doğrusal bağımsızlık konusuna bakınız. Determinantın bir başka kullanımı da, iki polinomun ortak bir köke sahip olup olmadığına dair bir ölçüt veren sonuçtur. ⓘ

Bir temelin yönelimi

Determinant, sütunları verilen vektörler olan kare matrisi kullanarak Rn'deki her n vektör dizisine bir sayı atamak olarak düşünülebilir. Örneğin, Rn'de girdileri olan bir ortogonal matris, Öklid uzayında ortonormal bir temeli temsil eder. Böyle bir matrisin determinantı, bazın yöneliminin standart bazın yönelimiyle tutarlı mı yoksa zıt mı olduğunu belirler. Eğer determinant +1 ise, temel aynı yönelime sahiptir. Eğer -1 ise, baz ters yönelimlidir. ⓘ

Daha genel olarak, A'nın determinantı pozitifse, A yönü koruyan bir doğrusal dönüşümü temsil eder (A ortogonal bir 2 × 2 veya 3 × 3 matris ise, bu bir rotasyondur), negatifse, A bazın yönünü değiştirir. ⓘ

Hacim ve Jacobian determinantı

Yukarıda belirtildiği gibi, reel vektörlerin determinantının mutlak değeri, bu vektörler tarafından yayılan paralel yüzeyin hacmine eşittir. Sonuç olarak, eğer $f:\mathbf {R} ^{n}\to \mathbf {R} ^{n}$ bir matris ile çarpılarak verilen doğrusal haritadır $A$ve $S\subset \mathbf {R} ^{n}$ ölçülebilir herhangi bir alt küme ise, o zaman $f(S)$ tarafından verilir $|\det(A)|$ hacminin iki katı $S$. Daha genel olarak, eğer doğrusal harita $f:\mathbf {R} ^{n}\to \mathbf {R} ^{m}$ tarafından temsil edilir. $m\times n$-matris $A$sonra $n$-boyutlu hacmi $f(S)$ tarafından verilir:

$\operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\operatorname {volume} (S).$ ⓘ

Dört nokta ile sınırlanan dörtyüzlünün hacmini hesaplayarak, eğri çizgileri tanımlamak için kullanılabilirler. Köşeleri verilen herhangi bir dörtyüzlünün hacmi $a,b,c,d$, ${\frac {1}{6}}\cdot |\det(a-b,b-c,c-d)|$veya köşeler üzerinde bir yayılan ağaç oluşturan köşe çiftlerinin başka herhangi bir kombinasyonu. ⓘ

Doğrusal olmayan bir harita $f\colon \mathbf {R} ^{2}\to \mathbf {R} ^{2}$ küçük bir kareyi (solda, kırmızı renkte) çarpıtılmış bir paralelkenara (sağda, kırmızı renkte) gönderir. Bir noktadaki Jacobian, o noktanın yakınındaki bozulmuş paralelkenarın en iyi doğrusal yaklaşımını verir (sağda, yarı saydam beyaz renkte) ve Jacobian determinantı, yaklaşan paralelkenarın alanının orijinal kareninkine oranını verir. ⓘ

Genel bir türevlenebilir fonksiyon için, yukarıdakilerin çoğu f'nin Jacobian matrisi göz önünde bulundurularak gerçekleştirilir.

$f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{n},$ ⓘ

Jacobian matrisi, girdileri kısmi türevler tarafından verilen n × n matrisidir

$D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.$ ⓘ

Bunun determinantı olan Jacobian determinantı, yerine koyarak integral almanın yüksek boyutlu versiyonunda ortaya çıkar: uygun f fonksiyonları ve Rn'nin açık bir U alt kümesi (f'nin etki alanı) için, başka bir φ : Rn → Rm fonksiyonunun f(U) üzerindeki integrali şu şekilde verilir

$\int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .$ ⓘ

Jacobian aynı zamanda ters fonksiyon teoreminde de yer alır. ⓘ

Haritacılık alanına uygulandığında determinant, kutuplara yakın bir haritanın genişleme oranını ölçmek için kullanılabilir. ⓘ

Soyut cebirsel yönler

Bir endomorfizmin determinantı

Çarpımların determinantı ve matrislerin tersleri ile ilgili yukarıdaki özdeşlikler, benzer matrislerin aynı determinanta sahip olduğunu ima eder: A = X-1BX olacak şekilde ters çevrilebilir bir X matrisi varsa, iki A ve B matrisi benzerdir. Gerçekten de, yukarıdaki özdeşlikleri tekrar tekrar uyguladığımızda ⓘ

$\det(A)=\det(X)^{-1}\det(B)\det(X)=\det(B)\det(X)^{-1}\det(X)=\det(B).$ ⓘ

Bu nedenle determinant benzerlik değişmezi olarak da adlandırılır. Doğrusal bir dönüşümün determinantı

$T:V\to V$

Bazı sonlu boyutlu vektör uzayı V için, V'deki keyfi bir temel seçimine göre onu tanımlayan matrisin determinantı olarak tanımlanır. Benzerlik değişmezliği ile, bu determinant V için temel seçiminden bağımsızdır ve bu nedenle sadece T endomorfizmine bağlıdır. ⓘ

Değişmeli halkalar üzerinde kare matrisler

Leibniz kuralını kullanan determinantın yukarıdaki tanımı, matrisin girdileri değişmeli bir halkanın elemanları olduğunda daha genel olarak geçerlidir $R$tam sayılar gibi $\mathbf {Z}$reel veya karmaşık sayılar alanının aksine. Dahası, determinantın aşağıdaki koşulları sağlayan tek alternatif çoklu doğrusal harita olarak nitelendirilmesi $\det(I)=1$ bu karakterizasyondan kaynaklanan tüm özellikler gibi hala geçerlidir. ⓘ

Bir matris $A\in \operatorname {Mat} _{n\times n}(R)$ ters çevrilebilirdir (yani, girdileri bir matrisin içinde olan bir ters matris vardır). $R$) ancak ve ancak determinantının ters çevrilebilir bir eleman olması durumunda $R$. İçin $R=\mathbf {Z}$bu, determinantın +1 veya -1 olduğu anlamına gelir. Böyle bir matris unimodüler olarak adlandırılır. ⓘ

Determinant çarpımsal olduğundan, bir grup homomorfizmi tanımlar

$\operatorname {GL} _{n}(R)\rightarrow R^{\times },$

genel doğrusal grup (ters çevrilebilir grup) arasında $n\times n$'de girdileri olan -matrisler $R$) ve birimlerin çarpımsal grubu $R$. Her iki grupta da çarpma işlemine saygı gösterdiğinden, bu harita bir grup homomorfizmidir. ⓘ

Determinant doğal bir dönüşümdür. ⓘ

Bir halka homomorfizması verildiğinde $f:R\to S$, bir harita var $\operatorname {GL} _{n}(f):\operatorname {GL} _{n}(R)\to \operatorname {GL} _{n}(S)$ 'deki tüm girdileri değiştirerek verilir. $R$ altındaki resimleriyle $f$. Determinant bu haritalara, yani özdeşliğe saygı gösterir

$f(\det((a_{i,j})))=\det((f(a_{i,j})))$

tutar. Başka bir deyişle, gösterilen değişmeli diyagram değişir. ⓘ

Örneğin, karmaşık bir matrisin karmaşık eşleniğinin determinantı (aynı zamanda eşlenik transpozesinin determinantıdır), determinantının karmaşık eşleniğidir ve tamsayı matrisler için: indirgeme modulo $m$ Böyle bir matrisin determinantı, matrisin modulo indirgenmiş determinantına eşittir. $m$ (ikinci determinant modüler aritmetik kullanılarak hesaplanır). Kategori teorisi dilinde, determinant iki funktör arasında doğal bir dönüşümdür $\operatorname {GL} _{n}$ ve $(-)^{\times }$. Bir başka soyutlama katmanı daha eklenerek, determinantın genel doğrusal gruptan çarpımsal gruba doğru bir cebirsel grup morfizmi olduğu söylenir,

$\det :\operatorname {GL} _{n}\to \mathbb {G} _{m}.$ ⓘ

Dış cebir

Doğrusal bir dönüşümün determinantı $T:V\to V$ bir $n$-boyutlu vektör uzayı $V$ veya daha genel olarak (sonlu) ranklı bir serbest modül $n$ değişmeli bir halka üzerinde $R$ dikkate alınarak koordinatsız bir şekilde formüle edilebilir. $n$-üçüncü dış güç $\bigwedge ^{n}V$ . $V$. Harita $T$ doğrusal bir harita indükler

${\begin{aligned}\bigwedge ^{n}T:\bigwedge ^{n}V&\rightarrow \bigwedge ^{n}V\\v_{1}\wedge v_{2}\wedge \dots \wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}$ ⓘ

As $\bigwedge ^{n}V$ tek boyutlu ise, harita $\bigwedge ^{n}T$ 'deki bir eleman gibi bir skaler ile çarpılarak verilir. $R$. (Bourbaki 1998) gibi bazı yazarlar bu gerçeği kullanarak determinantı $R$ aşağıdaki özdeşliği sağlamaktadır (tüm $v_{i}\in V$):

$\left(\bigwedge ^{n}T\right)\left(v_{1}\wedge \dots \wedge v_{n}\right)=\det(T)\cdot v_{1}\wedge \dots \wedge v_{n}.$ ⓘ

Bu tanım, daha somut olan koordinata bağlı tanım ile uyuşmaktadır. Bu, çoklu doğrusal alternatif formun tekliği kullanılarak gösterilebilir. $n$-'deki vektörlerin çiftleri $R^{n}$. Bu nedenle, sıfır olmayan en yüksek dış güç $\bigwedge ^{n}V$ (bir endomorfizma ile ilişkili determinantın aksine) bazen aşağıdakilerin determinantı olarak da adlandırılır $V$ ve benzer şekilde vektör demetleri veya vektör uzaylarının zincir kompleksleri gibi daha karmaşık nesneler için de geçerlidir. Bir matrisin minörleri de bu ortamda, alt alternatif formlar göz önünde bulundurularak oluşturulabilir $\bigwedge ^{k}V$ ile $k<n$. ⓘ

Genellemeler ve ilgili kavramlar

Yukarıda ele alındığı şekliyle determinantlar çeşitli varyantlara sahiptir: bir matrisin kalıcı değeri determinant olarak tanımlanır, ancak faktörler $\operatorname {sgn}(\sigma )$ Leibniz'in kuralında meydana gelenler ihmal edilmiştir. İmmanant, simetrik grubun bir karakterini tanıtarak her ikisini de genelleştirir $S_{n}$ Leibniz'in kuralında. ⓘ

Sonlu boyutlu cebirler için determinantlar

Herhangi bir ilişkisel cebir için $A$ cismi üzerinde bir vektör uzayı olarak sonlu boyutlu olan $F$, bir determinant haritası vardır ⓘ

$\det :A\to F.$

Bu tanım, determinanttan bağımsız olarak karakteristik polinomu belirleyerek ve determinantı bu polinomun en düşük dereceli terimi olarak tanımlayarak ilerler. Bu genel tanım, matris cebiri için determinantı geri kazandırır $A=\operatorname {Mat} _{n\times n}(F)$'nin yanı sıra bir kuaterniyonun determinantı da dahil olmak üzere birkaç başka durumu da içerir,

$\det(a+ib+jc+kd)=a^{2}+b^{2}+c^{2}+d^{2}$,

norm $N_{L/F}:L\to F$ Bir cisim genişlemesinin yanı sıra çarpık simetrik bir matrisin Pfaffian'ı ve merkezi basit bir cebirin indirgenmiş normu da bu yapının özel durumları olarak ortaya çıkar. ⓘ

Sonsuz matrisler

Sonsuz sayıda satır ve sütuna sahip matrisler için, determinantın yukarıdaki tanımları doğrudan taşınmaz. Örneğin, Leibniz formülünde, sonsuz bir toplamın (tüm terimleri sonsuz çarpım olan) hesaplanması gerekecektir. Fonksiyonel analiz, bu tür sonsuz boyutlu durumlar için determinantın farklı uzantılarını sağlar, ancak bunlar yalnızca belirli operatör türleri için işe yarar. ⓘ

Fredholm determinantı, iz sınıfı operatörler olarak bilinen operatörler için determinantı aşağıdaki formülün uygun bir genelleştirmesi ile tanımlar

$\det(I+A)=\exp(\operatorname {tr} (\log(I+A))).$ ⓘ

Sonsuz boyutlu bir başka determinant kavramı da fonksiyonel determinanttır. ⓘ

Von Neumann cebirlerinde operatörler

Sonlu bir faktördeki operatörler için, kanonik iz kullanılarak Fuglede-Kadison determinantı adı verilen pozitif gerçek değerli bir determinant tanımlanabilir. Aslında, bir von Neumann cebirindeki her üçlü duruma karşılık gelen bir Fuglede-Kadison determinantı kavramı vardır. ⓘ

Komütatif olmayan halkalar için ilgili kavramlar

Değişmeli olmayan halkalar üzerindeki matrisler için, n ≥ 2 için çoklu doğrusallık ve alternatif özellikler uyumsuzdur, bu nedenle bu ortamda determinantın iyi bir tanımı yoktur. ⓘ

Değişmeli olmayan bir halkada girdileri olan kare matrisler için, determinantları değişmeli halkalara benzer şekilde tanımlamada çeşitli zorluklar vardır. Çarpımın sırasının belirtilmesi koşuluyla Leibniz formülüne bir anlam verilebilir ve benzer şekilde determinantın diğer tanımları için de geçerlidir, ancak değişmeli olmama durumu determinantın çarpım özelliği ya da matrisin transpozisyonu altında determinantın değişmemesi gibi birçok temel özelliğinin kaybolmasına neden olur. Değişmeli olmayan halkalar üzerinde, makul bir çoklu doğrusal form kavramı yoktur (bazı argüman çiftlerinde değer olarak R'nin düzenli bir elemanına sahip sıfır olmayan bir bilineer formun varlığı, R'nin değişmeli olduğunu ima eder). Bununla birlikte, başta quasideterminantlar ve Dieudonné determinantı olmak üzere determinantların bazı özelliklerini koruyan çeşitli komütatif olmayan determinant kavramları formüle edilmiştir. Komütatif olmayan elemanlara sahip bazı matris sınıfları için determinant tanımlanabilir ve komütatif analoglarına çok benzeyen lineer cebir teoremleri kanıtlanabilir. Örnekler arasında kuantum gruplarında q-determinantı, Capelli matrislerinde Capelli determinantı ve süpermatrislerde Berezinian (yani, girdileri $\mathbb {Z} _{2}$-derecelendirilmiş halkalar). Manin matrisleri, değişmeli elemanları olan matrislere en yakın sınıfı oluşturur. ⓘ

Hesaplama

Determinantlar çoğunlukla teorik bir araç olarak kullanılır. Nümerik lineer cebirde nadiren açıkça hesaplanırlar; burada ters çevrilebilirliği kontrol etmek ve özdeğerleri bulmak gibi uygulamalar için determinantın yerini büyük ölçüde diğer teknikler almıştır. Bununla birlikte, hesaplamalı geometri determinantlarla ilgili hesaplamaları sıklıkla kullanır. ⓘ

Determinant doğrudan Leibniz kuralı kullanılarak hesaplanabilse de, bu yaklaşım büyük matrisler için son derece verimsizdir, çünkü bu formül $n!$ ($n$ için faktöriyel) ürünler $n\times n$-matrisidir. Böylece, gerekli işlemlerin sayısı çok hızlı bir şekilde artar: mertebe $n!$. Laplace açılımı da benzer şekilde verimsizdir. Bu nedenle, determinantları hesaplamak için daha kapsamlı teknikler geliştirilmiştir. ⓘ

Ayrıştırma yöntemleri

Bazı yöntemler şunları hesaplar $\det(A)$ matrisi, determinantları daha kolay hesaplanabilen matrislerin bir çarpımı olarak yazarak. Bu tür teknikler ayrıştırma yöntemleri olarak adlandırılır. Örnekler arasında LU ayrışımı, QR ayrışımı veya Cholesky ayrışımı (pozitif tanımlı matrisler için) yer alır. Bu yöntemlerin mertebesi $\operatorname {O} (n^{3})$'ye göre önemli bir gelişmedir. $\operatorname {O} (n!)$. ⓘ

Örneğin, LU ayrıştırması şunları ifade eder $A$ bir ürün olarak

$A=PLU.$

bir permütasyon matrisinin $P$ (tam olarak tek bir $1$ her sütunda ve aksi takdirde sıfırlar), bir alt üçgen matris $L$ ve bir üst üçgen matris $U$. İki üçgen matrisin determinantları $L$ ve $U$ ilgili köşegen girişlerinin çarpımları olduğundan hızlı bir şekilde hesaplanabilir. Determinantı $P$ sadece işarettir $\varepsilon$ karşılık gelen permütasyonun (ki bu $+1$ çift sayıda permütasyon için ve $-1$ tek sayıda permütasyon için). için böyle bir LU ayrışımı bilindiğinde $A$determinantı aşağıdaki gibi kolayca hesaplanabilir ⓘ

$\det(A)=\varepsilon \det(L)\cdot \det(U).$ ⓘ

Diğer yöntemler

Sipariş $\operatorname {O} (n^{3})$ ayrıştırma yöntemleriyle ulaşılan sonuçlar farklı yöntemlerle geliştirilmiştir. Eğer mertebeden iki matris $n$ zaman içinde çarpılabilir $M(n)$, nerede $M(n)\geq n^{a}$ Bazıları için $a>2$, o zaman determinantı zamanda hesaplayan bir algoritma vardır $O(M(n))$. Bunun anlamı, örneğin, bir $\operatorname {O} (n^{2.376})$ Coppersmith-Winograd algoritmasına dayanan bir algoritma mevcuttur. Bu üs, 2016 yılı itibariyle 2.373'e düşürülmüştür. ⓘ

Algoritmanın karmaşıklığına ek olarak, algoritmaları karşılaştırmak için başka kriterler de kullanılabilir. Özellikle halkalar üzerindeki matrislerle ilgili uygulamalar için, determinantı herhangi bir bölme işlemi yapmadan hesaplayan algoritmalar mevcuttur. (Buna karşın, Gauss eliminasyonu bölme işlemi gerektirir.) Karmaşıklığa sahip böyle bir algoritma $\operatorname {O} (n^{4})$ şu fikre dayanmaktadır: (Leibniz kuralında olduğu gibi) permütasyonların yerini, birkaç öğenin tekrarlanabildiği kapalı sıralı yürüyüşler alır. Ortaya çıkan toplam, Leibniz kuralından daha fazla terime sahiptir, ancak bu süreçte bu ürünlerin birçoğu yeniden kullanılabilir, bu da onu Leibniz kuralıyla saf bir şekilde hesaplamaktan daha verimli hale getirir. Algoritmalar ayrıca bit karmaşıklıklarına, yani hesaplamada ortaya çıkan ara değerleri saklamak için kaç bit doğruluk gerektiğine göre de değerlendirilebilir. Örneğin, Gauss eleme (veya LU ayrıştırma) yöntemi $\operatorname {O} (n^{3})$Ancak ara değerlerin bit uzunluğu üstel olarak uzun olabilir. Karşılaştırma yapmak gerekirse, Bareiss Algoritması tam bölme yöntemidir (yani bölmeyi kullanır, ancak yalnızca bu bölmelerin kalansız olarak gerçekleştirilebildiği durumlarda) aynı mertebededir, ancak bit karmaşıklığı kabaca matristeki orijinal girdilerin bit boyutu kadardır. $n$. ⓘ

A'nın determinantı ve A'nın tersi zaten hesaplanmışsa, matris determinantı lemması, u ve v'nin sütun vektörleri olduğu A + uv^T'nin determinantının hızlı bir şekilde hesaplanmasını sağlar. ⓘ

Charles Dodgson (yani Alice'in Harikalar Diyarında Maceraları kitabıyla ünlenen Lewis Carroll) determinantları hesaplamak için Dodgson yoğunlaştırması adı verilen bir yöntem icat etmiştir. Ne yazık ki bu ilginç yöntem her zaman orijinal haliyle çalışmaz. ⓘ

Determinantın açık tanımı

Determinantın açık tanımı bir A matrisinin kofaktörü C ya da minörü M cinsinden gösterilebilir:

$\det(A)=\sum _{j=1}^{n}A_{i,j}C_{i,j}=\sum _{j=1}^{n}A_{i,j}(-1)^{i+j}M_{i,j}$. ⓘ

Determinantın temel özellikleri

Kalıp Matrisler (Blok matrisler)

Boyutları n×n, n×m, m×n, ve m×m olan A, B, C, ve D matrislerinin olduğunu varsayalım. Bu matrisleri kullanarak n+m × n+m boyutunda büyük bir kare matris M oluşturalım. M'yi oluşturan A, B, C, ya da D kalıplarından herhangi birisi sıfır matris ise, M'nin determinantı kolayca hesaplanabilir:

$\det {\begin{pmatrix}{\mathsf {A}}&0\\{\mathsf {C}}&{\mathsf {D}}\end{pmatrix}}=\det {\begin{pmatrix}{\mathsf {A}}&{\mathsf {B}}\\0&{\mathsf {D}}\end{pmatrix}}={\mathsf {\det(A)\det(D)}}.$ ⓘ

Bu sonuç M matrisini iki matrisin çarpımı şekilde yazarak kolayca gösterilebilir. Anın tersi tanımlı olsun. Bu durumda ⓘ

${\begin{pmatrix}{\mathsf {A}}&{\mathsf {B}}\\{\mathsf {C}}&{\mathsf {D}}\end{pmatrix}}={\begin{pmatrix}{\mathsf {A}}&0\\{\mathsf {C}}&{\mathsf {I}}\end{pmatrix}}{\begin{pmatrix}{\mathsf {I}}&{\mathsf {A}}^{-1}{\mathsf {B}}\\0&{\mathsf {D-CA^{-1}B}}\end{pmatrix}}$ ⓘ

denkliği yazılabilir, ve buradan determinant ⓘ

$\det {\begin{pmatrix}{\mathsf {A}}&{\mathsf {B}}\\{\mathsf {C}}&{\mathsf {D}}\end{pmatrix}}={\mathsf {\det(A)\det(D-CA^{-1}B)}}.$ ⓘ

şeklinde hesaplanır. B ya da Cnin sıfır matris olması durumda yukarıdaki sonucu elde etimiş oluruz. ⓘ

Ayrıca, ⓘ

C ve Dnin değişme özelliği var ise, yani CD = DC ise, $\det {\begin{pmatrix}{\mathsf {A}}&{\mathsf {B}}\\{\mathsf {C}}&{\mathsf {D}}\end{pmatrix}}={\mathsf {\det(AD-BC)}}$. ⓘ

A ve Cnin değişme özelliği var ise, yani AC = CA ise, $\det {\begin{pmatrix}{\mathsf {A}}&{\mathsf {B}}\\{\mathsf {C}}&{\mathsf {D}}\end{pmatrix}}={\mathsf {\det(AD-CB)}}$. ⓘ

B ve Dnin değişme özelliği var ise, yani BD = DB ise, $\det {\begin{pmatrix}{\mathsf {A}}&{\mathsf {B}}\\{\mathsf {C}}&{\mathsf {D}}\end{pmatrix}}={\mathsf {\det(DA-BC)}}$. ⓘ

A ve Bnin değişme özelliği var ise, yani AB = BA ise, $\det {\begin{pmatrix}{\mathsf {A}}&{\mathsf {B}}\\{\mathsf {C}}&{\mathsf {D}}\end{pmatrix}}={\mathsf {\det(DA-CB)}}$. ⓘ