Polinom
| Fonksiyon ⓘ | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x ↦ f (x) | |||||||||||||||||||||||||||||
| tanım ve değer kümesine göre | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Sınıflar/özellikler | |||||||||||||||||||||||||||||
| Sabit · Birim · Doğrusal · Polinom · Rasyonel · Cebirsel · Analitik · Yumuşak · Sürekli · Ölçülebilir · Birebir · Örten · Birebir örten | |||||||||||||||||||||||||||||
| Yapılar | |||||||||||||||||||||||||||||
| Kısıtlama · Bileşim · λ · Terslik | |||||||||||||||||||||||||||||
| Genellemeler | |||||||||||||||||||||||||||||
| Parçalı · Çokdeğerli · Kapalı | |||||||||||||||||||||||||||||
Matematikte, bir polinom belirli sayıda bağımsız değişken ve sabit sayıdan oluşan bir ifadedir. Polinom kendi içinde toplama, çıkarma, çarpma ve negatif olmayan sayının üssünü alma işlemlerini kullanır. Örnek olarak tek bilinmeyenli bir polinom olan x2 − 4x + 7, ikinci dereceden bir polinomdur. Diğer bir örnek olarak, x2 − 4/x + 7x3/2 bir polinom değildir, çünkü polinomlarda terimlerin derecelerinin doğal sayı olması zorunludur. 2. terimde x′i ele alan bir bölme işlemi x'in derecesini negatif yapmaktadır ve 3. terim doğal sayı olmayan bir derece içermektedir (3/2). ⓘ
Polinomlar, bilimde ve matematik alanında sıkça görülür. Ekonomiden kimyaya, kimyadan fiziğe, ve sosyal bilimlerde problemlerin çözülmesi için kullanılır. Polinomlar, toplama işlemlerinde ve sayısal analizlerde diğer fonksiyonları belirlemek için kullanılır. İleri seviye matematikte, polinomlar, polinom halkaları oluşturmak için kullanılır, ve bu halkalar temel matematikte ve cebirsel geometride kullanılan merkezi bir kavramdır. ⓘ
Bu ismin akılda kalması amacıyla, Türk Dil Kurumu'nun da belirttiği polinom sözlük anlamıyla "çok terimli" anlamına gelmektedir. ⓘ
Etimoloji
Polinom kelimesi iki farklı kökü birleştirir: Yunanca poly, yani "çok" ve Latince nomen, yani "isim". Latince bi- kökünün Yunanca poly- ile değiştirilmesiyle binom teriminden türetilmiştir. Yani, birçok terimin (birçok tek terimli) toplamı anlamına gelir. Polinom kelimesi ilk olarak 17. yüzyılda kullanılmıştır. ⓘ
Gösterim ve terminoloji

Bir polinomda yer alan x genellikle değişken veya belirsiz olarak adlandırılır. Polinom bir ifade olarak düşünüldüğünde, x herhangi bir değeri olmayan sabit bir semboldür (değeri "belirsizdir"). Ancak, polinom tarafından tanımlanan fonksiyon düşünüldüğünde, x fonksiyonun argümanını temsil eder ve bu nedenle "değişken" olarak adlandırılır. Birçok yazar bu iki kelimeyi birbirinin yerine kullanmaktadır. ⓘ
Belirsiz x içinde bir P polinomu genellikle P veya P(x) olarak gösterilir. Biçimsel olarak, polinomun adı P(x) değil P'dir, ancak P(x) fonksiyonel gösteriminin kullanımı, polinom ve ilişkili fonksiyon arasındaki ayrımın belirsiz olduğu bir zamana dayanır. Dahası, fonksiyonel gösterim genellikle bir polinomu ve onun belirsizliğini tek bir cümleyle belirtmek için kullanışlıdır. Örneğin, "P(x) bir polinom olsun" ifadesi "P, x belirsizliğinde bir polinom olsun" ifadesinin kısaltmasıdır. Öte yandan, belirsizin adını vurgulamak gerekmediğinde, polinomun her oluşumunda belirsiz(ler)in ad(lar)ı görünmezse, birçok formül çok daha basit ve okunması daha kolaydır. ⓘ
Tek bir matematiksel nesne için iki gösterime sahip olmanın belirsizliği, polinomlar için fonksiyonel gösterimin genel anlamı göz önünde bulundurularak resmi olarak çözülebilir. Eğer a bir sayıyı, bir değişkeni, başka bir polinomu veya daha genel olarak herhangi bir ifadeyi gösteriyorsa, o zaman P(a), geleneksel olarak, P'de x yerine a koymanın sonucunu gösterir.
P ile ilişkili polinom fonksiyonudur. Bu gösterimi kullanırken genellikle a'nın bir sayı olduğu varsayılır. Ancak, toplama ve çarpmanın tanımlı olduğu herhangi bir alan (yani herhangi bir halka) üzerinde de kullanılabilir. Özellikle, eğer a bir polinom ise, P(a) da bir polinomdur. ⓘ
Daha spesifik olarak, a belirsiz x olduğunda, x'in bu fonksiyon tarafından görüntüsü P polinomunun kendisidir (x yerine x koymak hiçbir şeyi değiştirmez). Başka bir deyişle,
Bu da aynı polinom için iki gösterimin varlığını resmi olarak haklı çıkarır. ⓘ
Tanım
Bir polinom ifadesi, değişkenler veya belirsizlikler olarak adlandırılan sabitler ve sembollerden toplama, çarpma ve negatif olmayan bir tamsayı kuvvetine üs alma yoluyla oluşturulabilen bir ifadedir. Sabitler genellikle sayılardır, ancak belirsizlikleri içermeyen herhangi bir ifade olabilir ve toplanabilen ve çarpılabilen matematiksel nesneleri temsil eder. İki polinom ifadesi, toplama ve çarpmanın değişebilirlik, birleşebilirlik ve dağılabilirlik özellikleri uygulanarak biri diğerine dönüştürülebiliyorsa, aynı polinomu tanımlıyor olarak kabul edilir. Örneğin ve aynı polinomu temsil eden iki polinom ifadesidir; bu nedenle şöyle yazılır ⓘ
Tek bir x belirsizliğindeki bir polinom her zaman şu biçimde yazılabilir (veya yeniden yazılabilir)
nerede polinomun katsayıları olarak adlandırılan sabitlerdir ve belirsizdir. "Belirsiz" kelimesi şu anlama gelir belirli bir değeri temsil etmez, ancak yerine herhangi bir değer konulabilir. Bu ikame işleminin sonucunu ikame edilen değerle ilişkilendiren eşleme, polinom fonksiyonu olarak adlandırılan bir fonksiyondur. ⓘ
Bu, toplama notasyonu kullanılarak daha kısa bir şekilde ifade edilebilir:
Yani, bir polinom ya sıfır olabilir ya da sonlu sayıda sıfır olmayan terimin toplamı olarak yazılabilir. Her bir terim, terimin katsayısı olarak adlandırılan bir sayı ile negatif olmayan tam sayı kuvvetlerine yükseltilmiş sonlu sayıda belirsizliğin çarpımından oluşur. ⓘ
Sınıflandırma
Bir terimdeki belirsizin üssüne, o terimdeki belirsizin derecesi denir; terimin derecesi, o terimdeki belirsizlerin derecelerinin toplamıdır ve bir polinomun derecesi, katsayısı sıfır olmayan herhangi bir terimin en büyük derecesidir. x = x1 olduğundan, yazılı üssü olmayan bir belirsizin derecesi birdir. ⓘ
Belirsizliği olmayan bir terim ve belirsizliği olmayan bir polinom sırasıyla sabit terim ve sabit polinom olarak adlandırılır. Sabit bir terimin ve sıfır olmayan sabit bir polinomun derecesi 0'dır. 0 sıfır polinomunun derecesi (hiç terimi olmayan) genellikle tanımlanmamış olarak kabul edilir (ancak aşağıya bakınız). ⓘ
Örneğin:
bir terimdir. Katsayısı -5, belirsizlikleri x ve y, x'in derecesi iki, y'nin derecesi ise birdir. Tüm terimin derecesi, içindeki her bir belirsizin derecelerinin toplamıdır, yani bu örnekte derece 2 + 1 = 3'tür. ⓘ
Birkaç terimin toplamını oluşturmak bir polinom üretir. Örneğin, aşağıdaki bir polinomdur:
Üç terimden oluşur: birincisi ikinci derece, ikincisi birinci derece ve üçüncüsü sıfır derecedir. ⓘ
Küçük dereceli polinomlara özel isimler verilmiştir. Sıfırıncı dereceden bir polinom, sabit bir polinom ya da sadece bir sabittir. Bir, iki veya üç dereceli polinomlar sırasıyla doğrusal polinomlar, ikinci dereceden polinomlar ve kübik polinomlardır. Daha yüksek dereceler için, kuartik polinom (dördüncü derece için) ve kuintik polinom (beşinci derece için) bazen kullanılmasına rağmen, özel isimler yaygın olarak kullanılmaz. Derecelerin isimleri polinoma veya terimlerine uygulanabilir. Örneğin, x2 + 2x + 1'deki 2x terimi, ikinci dereceden bir polinomdaki doğrusal bir terimdir. ⓘ
Hiç terimi olmadığı düşünülebilen 0 polinomuna sıfır polinomu denir. Diğer sabit polinomların aksine, derecesi sıfır değildir. Bunun yerine, sıfır polinomunun derecesi ya açıkça tanımsız bırakılır ya da negatif olarak tanımlanır (-1 veya -∞). Sıfır polinomu, sonsuz sayıda kökü olan tek belirsiz polinom olması bakımından da benzersizdir. Sıfır polinomunun grafiği, f(x) = 0, x eksenidir. ⓘ
Birden fazla belirsizliğe sahip polinomlar söz konusu olduğunda, sıfır olmayan tüm terimlerinin derecesi n ise bir polinoma n dereceli homojen denir. Sıfır polinomu homojendir ve homojen bir polinom olarak derecesi tanımsızdır. Örneğin, x3y2 + 7x2y3 - 3x5 5. dereceden homojendir. Daha fazla ayrıntı için Homojen polinom bölümüne bakınız. ⓘ
Değişmeli toplama yasası, terimleri tercih edilen herhangi bir sıraya göre yeniden düzenlemek için kullanılabilir. Bir belirsizliği olan polinomlarda, terimler genellikle dereceye göre sıralanır, ya "x'in azalan kuvvetleri" şeklinde, en büyük dereceli terim önce olacak şekilde, ya da "x'in artan kuvvetleri" şeklinde. 3x2 - 5x + 4 polinomu x'in azalan kuvvetlerinde yazılır. İlk terimin katsayısı 3, belirsiz x ve üssü 2'dir. İkinci terimin katsayısı -5'tir. Üçüncü terim bir sabittir. Sıfır olmayan bir polinomun derecesi herhangi bir terimin en büyük derecesi olduğundan, bu polinomun derecesi ikidir. ⓘ
Aynı kuvvetlere yükseltilmiş aynı belirsizliklere sahip iki terim "benzer terimler" veya "benzer terimler" olarak adlandırılır ve dağılım yasası kullanılarak, katsayısı birleştirilen terimlerin katsayılarının toplamı olan tek bir terim halinde birleştirilebilirler. Polinomlar, katsayıları sıfır olmayan terimlerin sayısına göre sınıflandırılabilir, böylece bir terimli bir polinoma monomial, iki terimli bir polinoma binomial ve üç terimli bir polinoma trinomial denir. Dört terimli polinomlar için zaman zaman "quadrinomial" terimi kullanılır. ⓘ
Reel polinom, reel katsayıları olan bir polinomdur. Bir fonksiyonu tanımlamak için kullanıldığında, etki alanı bu kadar kısıtlı değildir. Ancak, gerçel polinom fonksiyonu gerçel polinom tarafından tanımlanan gerçellerden gerçellere bir fonksiyondur. Benzer şekilde, bir tamsayı polinomu tamsayı katsayılı bir polinomdur ve bir karmaşık polinom karmaşık katsayılı bir polinomdur. ⓘ
Bir belirsizliğe sahip bir polinoma tek değişkenli polinom, birden fazla belirsizliğe sahip bir polinoma ise çok değişkenli polinom denir. İki belirsizliği olan bir polinoma iki değişkenli polinom denir. Bu kavramlar, tek tek polinomlardan ziyade genel olarak çalışılan polinom türlerine atıfta bulunur; örneğin, tek değişkenli polinomlarla çalışırken, sabit polinomlar (sabit olmayan polinomların çıkarılmasından kaynaklanabilir) hariç tutulmaz, ancak kesin olarak konuşmak gerekirse, sabit polinomlar hiç belirsizlik içermez. Çok değişkenli polinomları, izin verilen maksimum belirsizlik sayısına göre iki değişkenli, üç değişkenli vb. olarak sınıflandırmak da mümkündür. Yine, incelenen nesneler kümesinin çıkarma işlemi altında kapalı olması için, üç değişkenli polinomlar üzerine yapılan bir çalışma genellikle iki değişkenli polinomlara izin verir ve bu böyle devam eder. Ayrıca, izin verilen belirsizlikleri listeleyerek basitçe "x, y ve z'de polinomlar" demek de yaygındır. ⓘ
Bir polinomun değerlendirilmesi, her bir belirsizliğin yerine sayısal bir değerin konulması ve belirtilen çarpma ve toplama işlemlerinin gerçekleştirilmesinden oluşur. Bir belirsizliğe sahip polinomlar için Horner yöntemi kullanılarak değerlendirme genellikle daha verimlidir (gerçekleştirilecek aritmetik işlem sayısı daha azdır):
Aritmetik
Toplama ve çıkarma
Polinomlar, muhtemelen yeniden sıralama (değişmeli yasa kullanılarak) ve benzer terimlerin birleştirilmesini takiben, birleşik toplama yasası (tüm terimlerini tek bir toplamda bir araya getirme) kullanılarak toplanabilir. Örneğin, eğer
- ve
o zaman toplam
olarak yeniden sıralanabilir ve yeniden gruplandırılabilir.
ve daha sonra basitleştirilerek
Polinomlar birbirine eklendiğinde, sonuç başka bir polinomdur. ⓘ
Polinomların çıkarılması da benzerdir. ⓘ
Çarpma işlemi
Polinomlar da çarpılabilir. İki polinomun çarpımını terimler toplamına genişletmek için, dağılım yasası tekrar tekrar uygulanır, bu da bir polinomun her teriminin diğerinin her terimiyle çarpılmasıyla sonuçlanır. Örneğin, eğer
sonra
Her terimde çarpma işleminin gerçekleştirilmesi
Benzer terimler bir araya getirildiğinde
olarak basitleştirilebilir.
Örnekte olduğu gibi, polinomların çarpımı her zaman bir polinomdur. ⓘ
Bileşim
Bir polinom verildiğinde tek değişkenli ve herhangi bir sayıda değişkenli başka bir g polinomunun bileşimi birinci polinomun değişkeninin her bir kopyasının ikinci polinomla yer değiştirmesiyle elde edilir. Örneğin, eğer ve sonra
Bölme işlemi
Bir polinomun diğerine bölümü tipik olarak bir polinom değildir. Bunun yerine, bu tür oranlar, bağlama bağlı olarak rasyonel kesirler, rasyonel ifadeler veya rasyonel fonksiyonlar olarak adlandırılan daha genel bir nesne ailesidir. Bu, iki tam sayının oranının mutlaka bir tam sayı değil, rasyonel bir sayı olması gerçeğine benzer. Örneğin, 1/(x2 + 1) kesri bir polinom değildir ve x değişkeninin kuvvetlerinin sonlu bir toplamı olarak yazılamaz. ⓘ
Tek değişkenli polinomlar için, tamsayıların Öklid bölme işlemini genelleştiren bir polinomların Öklid bölme işlemi kavramı vardır. Bu a(x)/b(x) bölme kavramı, a = b q + r ve derece(r) < derece(b) olacak şekilde iki polinom, bir bölüm q(x) ve bir kalan r(x) ile sonuçlanır. Bölüm ve kalan, polinom uzun bölme ve sentetik bölme dahil olmak üzere çeşitli algoritmalardan herhangi biri ile hesaplanabilir. ⓘ
Payda b(x) monik ve doğrusal olduğunda, yani bazı sabit c için b(x) = x - c olduğunda, polinom kalan teoremi a(x)'in b(x)'e bölümünden kalanın a(c) değerlendirmesi olduğunu ileri sürer. Bu durumda bölüm, sentetik bölmenin özel bir durumu olan Ruffini kuralı ile hesaplanabilir. ⓘ
Çarpanlara ayırma
Katsayıları benzersiz bir çarpanlara ayırma alanında (örneğin tam sayılar veya bir cisim) bulunan tüm polinomların, polinomun indirgenemez polinomlar ve bir sabitin çarpımı olarak yazıldığı çarpanlara ayrılmış bir biçimi de vardır. Bu çarpanlara ayrılmış form, çarpanların sırasına ve ters çevrilebilir bir sabitle çarpımlarına kadar benzersizdir. Karmaşık sayılar alanı söz konusu olduğunda, indirgenemez faktörler doğrusaldır. Reel sayılar üzerinde, bir ya da iki dereceye sahiptirler. Tam sayılar ve rasyonel sayılar üzerinde indirgenemez çarpanlar herhangi bir dereceye sahip olabilir. Örneğin, çarpanlarına ayrılmış biçimi
o
tamsayılar ve reel sayılar üzerinde ve
karmaşık sayılar üzerinde. ⓘ
Çarpanlara ayırma olarak adlandırılan çarpanlara ayrılmış formun hesaplanması, genel olarak, elle yazarak hesaplama ile yapılamayacak kadar zordur. Ancak, verimli polinom çarpanlarına ayırma algoritmaları çoğu bilgisayar cebir sisteminde mevcuttur. ⓘ
Kalkülüs
Polinomların türevlerini ve integrallerini hesaplamak, diğer fonksiyon türlerine kıyasla özellikle basittir. Polinomun türevi
Katsayıları daha soyut ortamlardan gelen polinomlar için (örneğin, katsayılar bazı p asal sayılarının modulo tamsayıları veya keyfi bir halkanın elemanları ise), türev formülü yine de kak katsayısının ak'nin k kopyasının toplamı anlamına geldiği anlaşılarak biçimsel olarak yorumlanabilir. Örneğin, modulo p tam sayıları üzerinde, xp + x polinomunun türevi 1 polinomudur. ⓘ
Polinom fonksiyonları
Bir polinom fonksiyonu, bir polinomun değerlendirilmesiyle tanımlanabilen bir fonksiyondur. Daha açık bir ifadeyle, verilen bir tanım alanından bir argümanı olan bir f fonksiyonu, eğer bir polinom varsa bir polinom fonksiyonudur
olarak değerlendiren f tanım alanındaki tüm x'ler için (burada n negatif olmayan bir tamsayıdır ve a0, a1, a2, ..., an sabit katsayılardır). Genel olarak, aksi belirtilmedikçe, polinom fonksiyonları karmaşık katsayılara, argümanlara ve değerlere sahiptir. Özellikle, reel katsayılarla sınırlandırılmış bir polinom, karmaşık sayılardan karmaşık sayılara doğru bir fonksiyon tanımlar. Bu fonksiyonun alanı da reellerle sınırlandırılırsa, ortaya çıkan fonksiyon reelleri reellere eşleyen bir reel fonksiyondur. ⓘ
Örneğin, f fonksiyonu şu şekilde tanımlanır
tek değişkenli bir polinom fonksiyonudur. Birden fazla değişkenin polinom fonksiyonları, benzer şekilde, birden fazla belirsizde polinomlar kullanılarak tanımlanır, örneğin
Polinom fonksiyonların tanımına göre, açıkça polinom olmayan ancak yine de polinom fonksiyonları tanımlayan ifadeler olabilir. Buna bir örnek şu ifadedir polinomu ile aynı değerleri alan aralıkta 'dir ve dolayısıyla her iki ifade de bu aralıkta aynı polinom fonksiyonunu tanımlar. ⓘ
Her polinom fonksiyonu sürekli, pürüzsüz ve tamdır. ⓘ
Hermit polinomları Pierre-Simon Laplace tarafından 1810'da zor anlaşılır bir biçimde tanımlanmış ve 1859'da Pafnuty Chebyshev tarafından ayrıntılı olarak incelenmiştir. Diğer klasik dik polinomlar gibi, Hermit polinomları birkaç farklı başlangıç noktasından tanımlanabilir. ⓘ

Grafikler
Tek gerçek değişkenli bir polinom fonksiyonu bir grafikle gösterilebilir.
-
Sıfır polinomunun grafiği
f(x) = 0x eksenidir.
-
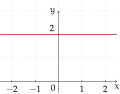
Derecesi 0 olan bir polinomun grafiği
f(x) = a0, burada a0 ≠ 0'dır,y-kesimi a0 olan yatay bir doğrudur
-
Derece 1 polinomun (veya doğrusal fonksiyonun) grafiği
f(x) = a0 + a1x, burada a1 ≠ 0'dır,y-kesişi a0 ve eğimi a1 olan eğik bir doğrudur.
-
Derece 2 polinomunun grafiği
f(x) = a0 + a1x + a2x2, burada a2 ≠ 0bir parabol.
-
Derece 3 polinomun grafiği
f(x) = a0 + a1x + a2x2 + a3x3, burada a3 ≠ 0kübik bir eğridir.
-
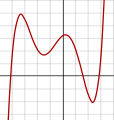
Derecesi 2 veya daha büyük olan herhangi bir polinomun grafiği
f(x) = a0 + a1x + a2x2 + ⋯ + anxn, burada an ≠ 0 ve n ≥ 2sürekli doğrusal olmayan bir eğridir. ⓘ
Sabit olmayan bir polinom fonksiyonu, değişken sonsuza kadar arttığında (mutlak değer olarak) sonsuza yönelir. Derecesi birden büyükse, grafiğin herhangi bir asimptotu yoktur. Dikey yönde iki parabolik dalı vardır (pozitif x için bir dal ve negatif x için bir dal). ⓘ
Polinom grafikleri hesapta kesişimler, eğimler, içbükeylik ve son davranış kullanılarak analiz edilir. ⓘ
Denklemler
Cebirsel denklem olarak da adlandırılan bir polinom denklemi, aşağıdaki formda bir denklemdir
Örneğin,
bir polinom denklemidir. ⓘ
Denklemler göz önünde bulundurulduğunda, polinomların belirsizlikleri (değişkenleri) bilinmeyenler olarak da adlandırılır ve çözümler, eşitliğin doğru olduğu bilinmeyenlerin olası değerleridir (genel olarak birden fazla çözüm mevcut olabilir). Bir polinom denklemi, (x + y)(x - y) = x2 - y2 gibi bir polinom özdeşliğinin aksine, her iki ifadenin de aynı polinomu farklı biçimlerde temsil ettiği ve sonuç olarak her iki üyenin de herhangi bir değerlendirmesinin geçerli bir eşitlik verdiği anlamına gelir. ⓘ
Temel cebirde, tek değişkenli tüm birinci ve ikinci derece polinom denklemlerini çözmek için ikinci dereceden formül gibi yöntemler öğretilir. Ayrıca kübik ve kuartik denklemler için de formüller vardır. Daha yüksek dereceler için, Abel-Ruffini teoremi radikallerde genel bir formül bulunamayacağını ileri sürer. Bununla birlikte, kök bulma algoritmaları, herhangi bir dereceden bir polinom ifadesinin köklerinin sayısal yaklaşımlarını bulmak için kullanılabilir. ⓘ
Reel katsayılı bir polinom denkleminin çözüm sayısı dereceyi aşamaz ve karmaşık çözümler çokluklarıyla birlikte sayıldığında dereceye eşit olur. Bu gerçeğe cebirin temel teoremi denir. ⓘ
Denklem çözme
Sıfır olmayan tek değişkenli bir P polinomunun kökü, P(a) = 0 olacak şekilde x'in bir a değeridir. Başka bir deyişle, P'nin bir kökü, P(x) = 0 polinom denkleminin bir çözümü veya P tarafından tanımlanan polinom fonksiyonunun bir sıfırıdır. Sıfır polinomu durumunda, her sayı ilgili fonksiyonun bir sıfırıdır ve kök kavramı nadiren dikkate alınır. ⓘ
Bir a sayısı, ancak ve ancak x - a doğrusal polinomu P'yi bölüyorsa, yani P = (x - a) Q olacak şekilde başka bir Q polinomu varsa, bir P polinomunun köküdür. x - a'nın bir kuvvetinin (1'den büyük) P'yi böldüğü de olabilir; bu durumda a, P'nin çoklu köküdür, aksi takdirde a, P'nin basit köküdür. Eğer P sıfırdan farklı bir polinom ise, (x - a)m'nin P'yi böleceği en yüksek m kuvveti vardır ve buna P'nin bir kökü olarak a'nın çokluğu denir. Sıfırdan farklı bir P polinomunun köklerinin sayısı, ilgili çokluklarıyla birlikte sayıldığında, P'nin derecesini aşamaz ve tüm karmaşık kökler dikkate alındığında bu dereceye eşit olur (bu, cebirin temel teoreminin bir sonucudur. Bir polinomun katsayıları ve kökleri Vieta'nın formülleri ile ilişkilidir. ⓘ
x2 + 1 gibi bazı polinomların gerçek sayılar arasında hiçbir kökü yoktur. Bununla birlikte, kabul edilen çözümler kümesi karmaşık sayılara genişletilirse, sabit olmayan her polinomun en az bir kökü vardır; bu cebirin temel teoremidir. Karmaşık katsayılı herhangi bir polinomun, x - a çarpanlarını art arda bölerek, bir sabit (baştaki katsayısı) ile 1. dereceden bu tür polinom çarpanlarının çarpımı olarak yazılabileceği görülür; sonuç olarak, çarpanlarıyla birlikte sayılan (karmaşık) köklerin sayısı tam olarak polinomun derecesine eşittir. ⓘ
"Bir denklemi çözmenin" çeşitli anlamları olabilir. Biri çözümleri açık sayılar olarak ifade etmek isteyebilir; örneğin, 2x - 1 = 0'ın tek çözümü 1/2'dir. Ne yazık ki bu, derecesi birden büyük olan denklemler için genel olarak imkansızdır ve eski zamanlardan beri matematikçiler çözümleri cebirsel ifadeler olarak ifade etmeye çalışmışlardır; örneğin altın oran 'nin tek pozitif çözümüdür. Eski zamanlarda, sadece bir ve iki derece için başarılı olmuşlardır. İkinci dereceden denklemler için ikinci dereceden formül, çözümlerin bu tür ifadelerini sağlar. 16. yüzyıldan bu yana, çok daha karmaşık olmasına rağmen, benzer formüller (kare köklere ek olarak küp kökler kullanılarak) üçüncü ve dördüncü derece denklemler için bilinmektedir (bkz. kübik denklem ve kuartik denklem). Ancak 5. ve daha yüksek dereceler için formüller birkaç yüzyıl boyunca araştırmacılardan kaçmıştır. 1824 yılında Niels Henrik Abel, çözümleri yalnızca aritmetik işlemler ve radikaller içeren (sonlu) bir formülle ifade edilemeyen 5. derece denklemler olduğuna dair çarpıcı sonucu kanıtladı (bkz. Abel-Ruffini teoremi). 1830'da Évariste Galois, dörtten yüksek dereceli denklemlerin çoğunun radikallerle çözülemeyeceğini kanıtladı ve her denklem için radikallerle çözülebilir olup olmadığına karar verilebileceğini ve eğer çözülebilirse çözülebileceğini gösterdi. Bu sonuç, modern cebirin iki önemli dalı olan Galois teorisi ve grup teorisinin başlangıcı oldu. Galois'in kendisi, yönteminin ima ettiği hesaplamaların uygulanamaz olduğunu belirtmiştir. Bununla birlikte, 5. ve 6. dereceden çözülebilir denklemler için formüller yayınlanmıştır (bkz. beşli fonksiyon ve seksik denklem). ⓘ
Kökler için cebirsel bir ifade olmadığında ya da böyle bir cebirsel ifade var olsa da kullanışlı olamayacak kadar karmaşık olduğunda, denklemi çözmenin tek yolu çözümlerin sayısal yaklaşımlarını hesaplamaktır. Bunun için birçok yöntem vardır; bazıları polinomlarla sınırlıdır ve diğerleri herhangi bir sürekli fonksiyona uygulanabilir. En verimli algoritmalar, 1.000'den yüksek dereceli polinom denklemlerinin (bilgisayarda) kolayca çözülmesini sağlar (bkz. Kök bulma algoritması). ⓘ
Birden fazla belirsizliği olan polinomlar için, polinom fonksiyonunun sıfır değerini aldığı değişkenlerin değer kombinasyonları genellikle "kökler" yerine sıfırlar olarak adlandırılır. Polinomların sıfır kümelerinin incelenmesi cebirsel geometrinin konusudur. Çok bilinmeyenli bir polinom denklemler kümesi için, sonlu sayıda karmaşık çözüme sahip olup olmadıklarına karar vermek ve bu sayı sonlu ise çözümleri hesaplamak için algoritmalar vardır. Polinom denklemler sistemine bakınız. ⓘ
Tüm polinomların birinci dereceden olduğu özel durum doğrusal denklem sistemi olarak adlandırılır ve bunun için klasik Gauss eliminasyonu da dahil olmak üzere bir dizi farklı çözüm yöntemi mevcuttur. ⓘ
Sadece tam sayı olan çözümleriyle ilgilenilen bir polinom denklemine Diophantine denklemi denir. Diophantine denklemlerini çözmek genellikle çok zor bir iştir. Bunları çözmek için, hatta çözüm kümesinin boş olup olmadığına karar vermek için bile genel bir algoritma bulunamayacağı kanıtlanmıştır (bkz. Hilbert'in onuncu problemi). Son elli yılda çözülen en ünlü problemlerden bazıları Fermat'ın Son Teoremi gibi Diophantine denklemleri ile ilgilidir. ⓘ
Polinom ifadeleri
Belirsizlerin diğer bazı matematiksel nesnelerle yer değiştirdiği polinomlar genellikle dikkate alınır ve bazen özel bir isme sahiptir. ⓘ
Trigonometrik polinomlar
Bir trigonometrik polinom, sin(nx) ve cos(nx) fonksiyonlarının sonlu bir doğrusal kombinasyonudur ve n bir veya daha fazla doğal sayı değerini alır. Gerçek değerli fonksiyonlar için katsayılar gerçek sayılar olarak alınabilir. ⓘ
Eğer sin(nx) ve cos(nx), sin(x) ve cos(x) cinsinden genişletilirse, trigonometrik bir polinom sin(x) ve cos(x) değişkenlerinde bir polinom haline gelir (Trigonometrik özdeşlikler listesi#Çoklu açı formülleri kullanılarak). Tersine, sin(x) ve cos(x)'teki her polinom, Çarpım-toplam özdeşlikleri ile sin(nx) ve cos(nx) fonksiyonlarının doğrusal bir kombinasyonuna dönüştürülebilir. Bu eşdeğerlik, doğrusal kombinasyonlara neden polinom denildiğini açıklar. ⓘ
Karmaşık katsayılar için, böyle bir fonksiyon ile sonlu Fourier serisi arasında bir fark yoktur. ⓘ
Trigonometrik polinomlar, örneğin periyodik fonksiyonların interpolasyonuna uygulanan trigonometrik interpolasyonda yaygın olarak kullanılır. Ayrıca ayrık Fourier dönüşümünde de kullanılırlar. ⓘ
Matris polinomları
Bir matris polinomu, değişkenleri kare matrisler olan bir polinomdur. Sıradan, skaler değerli bir polinom verildiğinde
A matrisinde değerlendirilen bu polinom
burada I kimlik matrisidir. ⓘ
Bir matris polinom denklemi, söz konusu belirli matrisler için geçerli olan iki matris polinomu arasındaki bir eşitliktir. Bir matris polinom özdeşliği, belirli bir Mn(R) matris halkasındaki tüm A matrisleri için geçerli olan bir matris polinom denklemidir. ⓘ
Üstel polinomlar
İkinci değişkenin birinci değişkene uygulanan üstel bir fonksiyonla yer değiştirdiği iki değişkenli bir polinom, örneğin P(x, ex), üstel polinom olarak adlandırılabilir. ⓘ
İlgili kavramlar
Rasyonel fonksiyonlar
Rasyonel kesir, iki polinomun bölümüdür (cebirsel kesir). Rasyonel kesir olarak yeniden yazılabilen herhangi bir cebirsel ifade rasyonel bir fonksiyondur. ⓘ
Polinom fonksiyonları değişkenlerin tüm değerleri için tanımlanırken, rasyonel bir fonksiyon yalnızca paydası sıfır olmayan değişkenlerin değerleri için tanımlanır. ⓘ
Rasyonel kesirler Laurent polinomlarını içerir, ancak paydaları bir belirsizin kuvvetleriyle sınırlamaz. ⓘ
Laurent polinomları
Laurent polinomları polinomlar gibidir, ancak değişken(ler)in negatif kuvvetlerinin oluşmasına izin verir. ⓘ
Güç serileri
Biçimsel kuvvet serileri polinomlar gibidir, ancak sonsuz sayıda sıfır olmayan terimin oluşmasına izin verir, böylece sonlu dereceye sahip olmazlar. Polinomların aksine, genel olarak açıkça ve tam olarak yazılamazlar (tıpkı irrasyonel sayıların yazılamaması gibi), ancak terimlerini manipüle etme kuralları polinomlarla aynıdır. Biçimsel olmayan güç serileri de polinomları genelleştirir, ancak iki güç serisinin çarpımı yakınsamayabilir. ⓘ
Polinom halkası
Değişmeli bir R halkası üzerindeki bir f polinomu, tüm katsayıları R'ye ait olan bir polinomdur. R üzerinde verilen bir belirsizlikler kümesindeki polinomların, bu belirsizliklerdeki polinom halkası olarak adlandırılan değişmeli bir halka oluşturduğunu doğrulamak kolaydır. tek değişkenli durumda ve çok değişkenli durumda. ⓘ
Biri var
Dolayısıyla, çok değişkenli durumun teorisinin çoğu yinelenen tek değişkenli duruma indirgenebilir. ⓘ
R'den R[x]'e r'yi kendisine sabit bir polinom olarak gönderen harita, R'nin R[x]'in bir alt halkası olarak görüldüğü enjektif bir halka homomorfizmidir. Özellikle, R[x], R üzerinde bir cebirdir. ⓘ
R[x] halkasını, R'ye yeni bir x elemanı ekleyerek ve minimal bir şekilde x'in zorunlu olanlar dışında başka hiçbir bağıntıyı sağlamadığı ve ayrıca R'nin tüm elemanlarıyla komütasyon sağladığı (yani xr = rx) bir halkaya genişleyerek R'den ortaya çıkan bir halka olarak düşünebiliriz. Bunu yapmak için, x'in tüm kuvvetlerini ve bunların doğrusal kombinasyonlarını da eklemek gerekir. ⓘ
Polinom halkasının oluşumu, idealleri çarpanlara ayırarak faktör halkaları oluşturmakla birlikte, bilinen halkalardan yeni halkalar oluşturmak için önemli araçlardır. Örneğin, karmaşık sayılar halkası (aslında alanı), x2 + 1 polinomunun katlarının idealini çarpanlarına ayırarak reel sayılar üzerindeki R[x] polinom halkasından oluşturulabilir. Bir başka örnek de, R katsayı halkası olarak bazı asal sayıları modüle eden tam sayılar alanından başlayarak benzer şekilde ilerleyen sonlu alanların inşasıdır (bkz. modüler aritmetik). ⓘ
Eğer R değişmeli ise, R[x]'deki her P polinomu ile etki alanı ve aralığı R'ye eşit olan bir f polinom fonksiyonu ilişkilendirilebilir (Daha genel olarak, etki alanı ve aralığı R üzerindeki herhangi bir aynı birleşik cebir olarak alınabilir). Polinomlar ve polinom fonksiyonları arasında ayrım yapmanın bir nedeni, bazı halkalar üzerinde farklı polinomların aynı polinom fonksiyonuna yol açabilmesidir (R'nin modulo p tam sayıları olduğu bir örnek için Fermat'ın küçük teoremine bakın). R reel veya karmaşık sayılar olduğunda durum böyle değildir, bu nedenle iki kavram analizde her zaman ayırt edilmez. Polinomlar ve polinom fonksiyonları arasında ayrım yapmanın daha da önemli bir nedeni, polinomlar üzerindeki birçok işlemin (Öklid bölmesi gibi), bir polinomu x için sabit bir değerde değerlendirmek yerine bir ifade olarak nelerden oluştuğuna bakmayı gerektirmesidir. ⓘ
Bölünebilirlik
Eğer R bir integral bölgesi ve f ve g R[x]'te polinomlar ise, R[x]'te f q = g olacak şekilde bir q polinomu varsa, f'nin g'yi böldüğü veya f'nin g'nin bir bölen olduğu söylenir. o zaman a, f'nin bir köküdür, ancak ve ancak Bu durumda, bölüm polinom uzun bölme kullanılarak hesaplanabilir. ⓘ
Eğer F bir cisim ve f ve g F[x] içinde g ≠ 0 olan polinomlar ise, F[x] içinde q ve r polinomları vardır ve
ve öyle ki r'nin derecesi g'nin derecesinden küçüktür (0 polinomunun negatif dereceye sahip olduğu kuralını kullanarak). q ve r polinomları f ve g tarafından benzersiz bir şekilde belirlenir. Buna Öklid bölme, kalanlı bölme veya polinom uzun bölme denir ve F[x] halkasının bir Öklid bölgesi olduğunu gösterir. ⓘ
Benzer şekilde, asal polinomlar (daha doğrusu indirgenemez polinomlar), sabit olmayan iki polinomun çarpımına çarpanlarına ayrılamayan sıfır olmayan polinomlar olarak tanımlanabilir. Bir halkadaki katsayılar söz konusu olduğunda, "sabit olmayan" ifadesi "sabit olmayan veya birim olmayan" ifadesiyle değiştirilmelidir (bir cisimdeki katsayılar söz konusu olduğunda her iki tanım da aynıdır). Herhangi bir polinom, indirgenemez polinomların bir çarpımı ile ters çevrilebilir bir sabitin çarpımına ayrıştırılabilir. Eğer katsayılar bir cisme veya benzersiz bir çarpanlara ayırma alanına aitse, bu ayrıştırma çarpanların sırasına ve birim olmayan herhangi bir çarpanın bir birimle çarpımına (ve birim çarpanın aynı birimle bölümüne) kadar benzersizdir. Katsayılar tam sayılara, rasyonel sayılara veya sonlu bir alana ait olduğunda, indirgenemezliği test etmek ve indirgenemez polinomlara çarpanlara ayırmayı hesaplamak için algoritmalar vardır (bkz. Polinomların çarpanlara ayrılması). Bu algoritmalar elle hesaplama için pratik değildir, ancak herhangi bir bilgisayar cebir sisteminde mevcuttur. Eisenstein kriteri de bazı durumlarda indirgenemezliği belirlemek için kullanılabilir. ⓘ
Uygulamalar
Konumsal gösterim
Ondalık sistem gibi modern konumsal sayı sistemlerinde, bir tam sayının gösterimindeki rakamlar ve konumları, örneğin 45, radiks veya tabandaki bir polinomun kısaltılmış gösterimidir, bu durumda 4 × 101 + 5 × 100. Başka bir örnek olarak, radix 5'te 132 gibi bir rakam dizisi (ondalık) 1 × 52 + 3 × 51 + 2 × 50 = 42 sayısını gösterir. Bu gösterim benzersizdir. b, 1'den büyük pozitif bir tamsayı olsun. O zaman her pozitif a tamsayısı aşağıdaki biçimde benzersiz olarak ifade edilebilir ⓘ
Burada m negatif olmayan bir tamsayıdır ve r'ler aşağıdaki gibi tamsayılardır ⓘ
- 0 < rm < b ve i = 0, 1, ... için 0 ≤ ri < b. , m - 1. ⓘ
Enterpolasyon ve yaklaşım
Polinom fonksiyonlarının basit yapısı, onları polinom yaklaşımları kullanarak genel fonksiyonları analiz etmede oldukça kullanışlı kılar. Kalkülüste önemli bir örnek, kabaca her türevlenebilir fonksiyonun yerel olarak bir polinom fonksiyona benzediğini belirten Taylor teoremi ve reel eksenin kompakt bir aralığında tanımlanan her sürekli fonksiyonun tüm aralıkta bir polinom fonksiyon tarafından istenildiği kadar yaklaştırılabileceğini belirten Stone-Weierstrass teoremidir. Pratik yaklaşım yöntemleri arasında polinom interpolasyonu ve spline kullanımı yer alır. ⓘ
Diğer uygulamalar
Polinomlar sıklıkla başka bir nesne hakkında bilgi kodlamak için kullanılır. Bir matrisin veya doğrusal operatörün karakteristik polinomu, operatörün özdeğerleri hakkında bilgi içerir. Bir cebirsel elemanın minimal polinomu, o eleman tarafından sağlanan en basit cebirsel ilişkiyi kaydeder. Bir grafiğin kromatik polinomu, o grafiğin uygun renklendirmelerinin sayısını sayar. ⓘ
"Polinom" terimi, bir sıfat olarak, polinom biçiminde yazılabilen nicelikler veya fonksiyonlar için de kullanılabilir. Örneğin, hesaplama karmaşıklığı teorisinde polinom zaman ifadesi, bir algoritmayı tamamlamak için gereken sürenin, girdinin boyutu gibi bazı değişkenlerin polinom bir fonksiyonu ile sınırlandırıldığı anlamına gelir. ⓘ
Tarih
Polinomların köklerini belirlemek ya da "cebirsel denklemleri çözmek" matematiğin en eski problemleri arasındadır. Bununla birlikte, bugün kullandığımız zarif ve pratik notasyon ancak 15. yüzyıldan itibaren gelişmiştir. Ondan önce denklemler kelimelerle yazılırdı. Örneğin, M.Ö. 200'lere ait Dokuz Bölümde Çin Aritmetiği'ndeki bir cebir problemi şöyle başlar: "Üç demet iyi ürün, iki demet vasat ürün ve bir demet kötü ürün 29 dou'ya satıldı." Biz 3x + 2y + z = 29 yazacağız. ⓘ
Notasyonun tarihçesi
Eşittir işaretinin bilinen en eski kullanımı Robert Recorde'un 1557 tarihli The Whetstone of Witte adlı eserindedir. Toplama için +, çıkarma için - işaretleri ve bilinmeyen için bir harf kullanımı Michael Stifel'in Arithemetica integra, 1544 adlı eserinde görülür. René Descartes, 1637 tarihli La géometrie'de bir polinom denkleminin grafiği kavramını tanıtmıştır. Yukarıda görülebileceği gibi, a'ların sabitleri ve x'in bir değişkeni gösterdiği tek değişkenli bir polinomun genel formülünde sabitleri belirtmek için alfabenin başındaki harflerin ve değişkenleri belirtmek için alfabenin sonundaki harflerin kullanımını yaygınlaştırmıştır. Descartes üsleri belirtmek için üst simge kullanımını da getirmiştir. ⓘ
Tanım
Olaslıkçıların kullandığı Hermit polinomu; ⓘ
Fizikçilerin kullandığı Hermit polinomu; ⓘ
Olasılıkçıların kullandığı Hermit polinomunun ilk on bir değeri; ⓘ
Özellikleri
Diklik
ve dereceden polinomları için Bu polinomlar ağırlık işlevine(fonksiyon) göre dikliktir. ⓘ
için) ⓘ
ya da ⓘ
( için) ⓘ










































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)




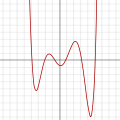







![{\displaystyle R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce54622cb380383ab3a42441b056626ea0d2440)
![{\displaystyle R[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c388e003e234e12fb55533e35a211c8cf295e5)
![{\displaystyle R[x_{1},\ldots ,x_{n}]=\left(R[x_{1},\ldots ,x_{n-1}]\right)[x_{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0bbfe1bccac6aa10e3a7daba9b95381c6f05bd)
























