Matematik
| Makale serilerinden ⓘ |
Bilim |
|---|
|
Bilim portalı Kategori |

Matematik (Yunanca μάθημα máthēma, "bilgi, çalışma, öğrenme"); numaralar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır. ⓘ
Matematikçiler örüntüleri araştırır ve bunları yeni konjektürler formüle etmekte kullanırlar. Bu konjektürlerin doğruluğunu veya yanlışlığını matematiksel ispat yoluyla çözmeye çalışırlar. Matematiksel yapılar gerçek fenomenleri iyi modelize ettiklerinde matematiksel düşünce doğa hakkında tahmin yürütmemizi ve onun iç yüzünü anlamamızı sağlayabilir. Matematik soyutlama ve mantığı kullanarak ve sistemli çalışmayla fiziksel objelerin şekillerini ve hareketlerini saymayı, hesaplamayı ve ölçmeyi mümkün kılar ve böylece gelişir. Pratik matematik yazılı kayıtlardan beri insan etkinliği olagelmiştir. Matematik problemlerinin çözümü için gerekli araştırma yıllarca hatta yüzyıllarca süren bir çaba gerektirebilir. ⓘ
İlk titiz kayıtlara Yunan matematiğinde rastlanır. (Özellikle Öklid'in Elementler kitabında) Giuseppe Peano (1858-1932), David Hilbert (1862-1943) ve diğerlerinin geç 19 yüzyılda belitsel sistemler üzerine kurdukları çalışmalarından beri matematiksel araştırmada doğruyu kurmanın geleneği değişti. (Artık uygun olarak seçilen aksiyom ve tanımlardan titiz bir şekilde tümdengelim yapılmaktadır.) Matematik Rönesans'a kadar görece yavaş gelişti. Sonra matematikteki yenilikler diğer yeni bilimsel keșiflerle etkileșerek matematiksel keșiflerde günümüzde hala devam eden hızlı bir artış sağladı. ⓘ
Galileo Galilei (1564-1642) "Kainat dediğimiz kitap, yazıldığı dil ve harfler öğrenilmedikçe anlaşılamaz. O, matematik dilinde yazılmış; harfleri üçgen, daire ve diğer geometrik şekillerdir. Bu dil ve harfler olmaksızın kitabın tek bir kelimesinin anlaşılmasına olanak yoktur. Bunlar olmaksızın yapılan karanlık bir labirentte amaçsızca dolaşmaktır." Carl Friedrich Gauss (1777-1855) matematiği bilimlerin kraliçesine benzetmiştir. Benjamin Peirce (1809-1880) matematik için bilimlerin sonuçlarının çizilmesi için gereken bilim demiştir. David Hilbert "Biz burada gelişigüzel konuşmayız. Matematik şart koşulan rastgele kuralların olduğu bir oyun gibi değildir. O yalnızca içsel gerekliliğin olduğu kavramsal bir sistemdir, aksi hiçbir şey değil." Albert Einstein (1879-1955), "Matematik kesin olduğunda gerçeği yansıtmaz, gerçeği yansıttığında kesin değildir." Fransız matematikçi Claire Voisin, "Matematikte yaratıcı itki, her yerinde kendini ifade etmeyi denemesidir." der. ⓘ
Matematik dünya genelinde doğa bilimleri, mühendislik, teknoloji ve maliye gibi birçok alanın temel aracıdır. Uygulamalı matematik, matematiksel bilginin diğer alanlara uygulanmasıyla ilgilidir. Bu uygulamalar sayesinde istatistik ve oyun teorisi gibi tamamıyla yeni matematik disiplinleri doğmuştur. Ayrıca matematikçiler soyut matematikle akıllarında herhangi bir kullanım olmadan da yalnızca matematik yapmak için uğraşırlar. Soyut matematikle uygulamalı matematiği ayıran belirgin bir çizgi yoktur. Soyut matematikteki keşifler sıklıkla pratik matematik uygulamalarının başlatıcısı olurlar. ⓘ
 | ||
| Matematik | ||
|---|---|---|
|
|
||
| Makaleler | ||
|
||
| Bilim İnsanları | ||
|
||
| Navigasyon | ||
|
||

Matematiksel faaliyetlerin çoğu, soyut nesnelerin özelliklerini saf akıl yürütme yoluyla keşfetmeyi ve kanıtlamayı içerir. Bu nesneler ya doğal sayılar veya çizgiler gibi doğadan soyutlamalardır ya da - modern matematikte - aksiyom olarak adlandırılan belirli özelliklere sahip varlıklar. Bir ispat, daha önce ispatlanmış teoremler, aksiyomlar ve (doğadan soyutlama durumunda) söz konusu teorinin gerçek başlangıç noktaları olarak kabul edilen bazı temel özellikler de dahil olmak üzere, halihazırda bilinen sonuçlara bazı tümdengelim kurallarının art arda uygulanmasından oluşur. Bir ispatın sonucuna teorem adı verilir. ⓘ
Matematik, fenomenleri modellemek için bilimde yaygın olarak kullanılmaktadır. Bu, deneysel yasalardan nicel tahminlerin çıkarılmasını sağlar. Örneğin, gezegenlerin hareketi Newton'un yerçekimi kanunu matematiksel hesaplama ile birlikte kullanılarak doğru bir şekilde tahmin edilebilir. Matematiksel gerçeğin herhangi bir deneyden bağımsız olması, bu tür tahminlerin doğruluğunun yalnızca modelin gerçekliği tanımlama yeterliliğine bağlı olduğu anlamına gelir. Yanlış tahminler matematiksel modellerin iyileştirilmesi ya da değiştirilmesi ihtiyacına işaret eder, modellerin kendilerinin yanlış olduğuna değil. Örneğin, Merkür'ün perihelion presesyonu Newton'un kütle çekim yasası ile açıklanamaz, ancak Einstein'ın genel göreliliği ile doğru bir şekilde açıklanır. Einstein'ın teorisinin bu deneysel doğrulaması, Newton'un kütle çekim yasasının günlük uygulamada doğru olsa da sadece bir yaklaşım olduğunu göstermektedir. ⓘ
Tarihsel olarak, ispat kavramı ve buna bağlı matematiksel titizlik ilk olarak Yunan matematiğinde, özellikle de Öklid'in Elementler'inde ortaya çıkmıştır. Başlangıcından bu yana matematik, cebir ve sonsuz küçükler hesabının yeni alanlar olarak tanıtıldığı 16. ve 17. yüzyıllara kadar esasen geometri ve aritmetik (doğal sayıların ve kesirlerin manipülasyonu) olarak ikiye ayrılmıştır. O zamandan beri, matematiksel yenilikler ve bilimsel keşifler arasındaki etkileşim, matematiğin gelişiminde hızlı bir artışa yol açmıştır. 19. yüzyılın sonunda matematiğin yaşadığı temel kriz, aksiyomatik yöntemin sistematik hale gelmesine yol açmıştır. Bu da matematik alanlarının ve bunların uygulama alanlarının sayısında dramatik bir artışa yol açmıştır. Bunun bir örneği, matematiğin altmıştan fazla birinci düzey alanını listeleyen Matematik Konu Sınıflandırmasıdır. ⓘ
Matematik alanları
Rönesans'tan önce matematik iki ana alana ayrılıyordu: sayıların manipülasyonuyla ilgili olan aritmetik ve şekillerin incelenmesiyle ilgili olan geometri. Numeroloji ve astroloji gibi bazı sözde bilim türleri o zamanlar matematikten açıkça ayırt edilmiyordu. ⓘ
Rönesans sırasında iki alan daha ortaya çıktı. Matematiksel notasyon, kabaca formüllerin incelenmesi ve manipülasyonundan oluşan cebire yol açtı. Sonsuz küçükler hesabı ve integral hesabı olmak üzere iki alt alandan oluşan kalkülüs, değişen nicelikler (değişkenler) arasındaki tipik doğrusal olmayan ilişkileri modelleyen sürekli fonksiyonların incelenmesidir. Aritmetik, geometri, cebir ve kalkülüs olmak üzere dört ana alana ayrılan bu bölüm 19. yüzyılın sonuna kadar devam etmiştir. Gök mekaniği ve katı mekaniği gibi alanlar o zamanlar genellikle matematiğin bir parçası olarak kabul edilirdi, ancak şimdi fiziğe ait olarak kabul edilmektedir. Bu dönemde geliştirilen bazı konular matematiğin öncesine dayanır ve olasılık teorisi ve kombinatorik gibi alanlara ayrılır, ancak bunlar daha sonra özerk alanlar olarak kabul edilmiştir. ⓘ
19. yüzyılın sonunda matematikte yaşanan temel kriz ve bunun sonucunda aksiyomatik yöntemin sistematik hale gelmesi, matematiğin yeni alanlarında bir patlamaya yol açmıştır. Bugün, Matematik Konu Sınıflandırması en az altmış dört birinci düzey alan içermektedir. Bu alanlardan bazıları, sayılar teorisi (yüksek aritmetiğin modern adı) ve geometride olduğu gibi, daha eski bölümlere karşılık gelmektedir. (Bununla birlikte, diğer bazı birinci düzey alanların adlarında "geometri" vardır veya yaygın olarak geometrinin bir parçası olarak kabul edilirler). Cebir ve kalkülüs birinci seviye alanlar olarak görünmezler ancak sırasıyla birkaç birinci seviye alana ayrılırlar. Matematiksel mantık ve temeller (model teorisi, hesaplanabilirlik teorisi, küme teorisi, ispat teorisi ve cebirsel mantık dahil) gibi diğer birinci düzey alanlar 20. yüzyılda ortaya çıkmıştır (örneğin kategori teorisi; homolojik cebir ve bilgisayar bilimi) veya daha önce matematik olarak kabul edilmemiştir. ⓘ
Sayı teorisi

Sayılar teorisi, sayıların, yani doğal sayıların manipülasyonu ile başladı ve daha sonra tam sayılara genişletildi ve rasyonel sayılar Eskiden sayı teorisi aritmetik olarak adlandırılırdı, ancak günümüzde bu terim daha çok sayısal hesaplamalar için kullanılmaktadır. ⓘ
Kolayca ifade edilen birçok sayı problemi, matematiğin her alanından sofistike yöntemler gerektiren çözümlere sahiptir. Öne çıkan örneklerden biri Fermat'nın son teoremidir. Bu varsayım 1637 yılında Pierre de Fermat tarafından ifade edilmiştir, ancak ancak 1994 yılında cebirsel geometriden şema teorisi, kategori teorisi ve homolojik cebir gibi araçları kullanan Andrew Wiles tarafından kanıtlanmıştır. Bir başka örnek de 2'den büyük her çift tam sayının iki asal sayının toplamı olduğunu ileri süren Goldbach varsayımıdır. Christian Goldbach tarafından 1742 yılında ortaya atılan bu varsayım, büyük çabalara rağmen bugüne kadar kanıtlanamamıştır. ⓘ
Sayılar teorisi analitik sayılar teorisi, cebirsel sayılar teorisi, sayılar geometrisi (yöntem odaklı), diophantine denklemleri ve aşkınlık teorisi (problem odaklı) gibi çeşitli alt alanları içerir. ⓘ
Geometri
Geometri matematiğin en eski dallarından biridir. Esas olarak ölçme ve mimarinin ihtiyaçları için geliştirilen çizgiler, açılar ve daireler gibi şekillerle ilgili deneysel tariflerle başlamış, ancak o zamandan beri diğer birçok alt alana dönüşmüştür. ⓘ
Temel bir yenilik, her iddianın kanıtlanması gerekliliği ile antik Yunanlılar tarafından ispat kavramının ortaya atılmasıdır. Örneğin, iki uzunluğun eşit olduğunu ölçümle doğrulamak yeterli değildir; bunların eşitliği daha önce kabul edilmiş sonuçlardan (teoremler) ve birkaç temel ifadeden akıl yürütme yoluyla kanıtlanmalıdır. Temel önermeler ispata tabi değildir çünkü bunlar apaçıktır (postulatlar) ya da çalışma konusunun tanımının bir parçasıdır (aksiyomlar). Tüm matematiğin temelini oluşturan bu ilke ilk olarak geometri için geliştirilmiş ve Öklid tarafından M.Ö. 300 yıllarında Elementler adlı kitabında sistematik hale getirilmiştir. ⓘ
Sonuçta ortaya çıkan Öklid geometrisi, Öklid düzleminde (düzlem geometrisi) ve (üç boyutlu) Öklid uzayında doğrulardan, düzlemlerden ve dairelerden inşa edilen şekillerin ve bunların düzenlemelerinin incelenmesidir. ⓘ
Öklid geometrisi, René Descartes'ın günümüzde Kartezyen koordinatlar olarak adlandırılan yöntemi ortaya attığı 17. yüzyıla kadar yöntem ya da kapsam değişikliği olmaksızın geliştirilmiştir. Bu büyük bir paradigma değişikliğiydi, çünkü gerçek sayıları doğru parçalarının uzunlukları olarak tanımlamak yerine (bkz. sayı doğrusu), noktaların koordinatları (ki bunlar sayılardır) kullanılarak temsil edilmesine izin verdi. Bu, geometrik problemleri çözmek için cebir (ve daha sonra kalkülüs) kullanılmasına izin verir. Bu, geometriyi iki yeni alt alana ayırdı: tamamen geometrik yöntemler kullanan sentetik geometri ve koordinatları sistematik olarak kullanan analitik geometri. ⓘ
Analitik geometri, çemberler ve doğrularla ilgili olmayan eğrilerin incelenmesine izin verir. Bu tür eğriler fonksiyonların grafiği olarak tanımlanabilir (çalışmaları diferansiyel geometriye yol açmıştır). Ayrıca örtük denklemler, genellikle polinom denklemleri (cebirsel geometriyi ortaya çıkaran) olarak da tanımlanabilirler. Analitik geometri aynı zamanda üç boyuttan daha büyük uzayların ele alınmasını da mümkün kılar. ⓘ
19. yüzyılda matematikçiler, paralel postülasına uymayan Öklid dışı geometrileri keşfettiler. Bu postülatın doğruluğunu sorgulayan bu keşif, matematiğin temel krizini ortaya koyan Russel paradoksuna katılır. Krizin bu yönü, aksiyomatik yöntemin sistematik hale getirilmesi ve seçilen aksiyomların doğruluğunun matematiksel bir sorun olmadığının kabul edilmesiyle çözülmüştür. Buna karşılık aksiyomatik yöntem, aksiyomların değiştirilmesiyle ya da uzayın belirli dönüşümleri altında değişmeyen özelliklerin dikkate alınmasıyla elde edilen çeşitli geometrilerin incelenmesine izin verir. ⓘ
Günümüzde geometrinin alt alanları şunları içerir:
- Girard Desargues tarafından 16. yüzyılda tanıtılan projektif geometri, paralel doğruların kesiştiği sonsuzdaki noktaları ekleyerek Öklid geometrisini genişletir. Bu, kesişen ve paralel çizgiler için tedavileri birleştirerek klasik geometrinin birçok yönünü basitleştirir.
- Afin geometri, paralellik ile ilgili ve uzunluk kavramından bağımsız özelliklerin incelenmesi.
- Diferansiyel geometri, türevlenebilir fonksiyonlar kullanılarak tanımlanan eğrilerin, yüzeylerin ve bunların genellemelerinin incelenmesi
- Manifold teorisi, daha büyük bir uzaya gömülü olması gerekmeyen şekillerin incelenmesi
- Riemann geometrisi, eğri uzaylarda uzaklık özelliklerinin incelenmesi
- Cebirsel geometri, polinomlar kullanılarak tanımlanan eğrilerin, yüzeylerin ve bunların genelleştirmelerinin incelenmesi
- Topoloji, sürekli deformasyonlar altında korunan özelliklerin incelenmesi
- Cebirsel topoloji, başta homolojik cebir olmak üzere cebirsel yöntemlerin topolojide kullanımı
- Ayrık geometri, geometride sonlu konfigürasyonların incelenmesi
- Konveks geometri, önemini optimizasyondaki uygulamalarından alan konveks kümelerin incelenmesi
- Karmaşık geometri, gerçek sayıların karmaşık sayılarla değiştirilmesiyle elde edilen geometri ⓘ
ⓘ




Geometri Trigonometri Diferansiyel geometri Topoloji Fraktal geometri
Cebir
Cebir, denklemleri ve formülleri manipüle etme sanatıdır. Diophantus (3. yüzyıl) ve Harezmi (9. yüzyıl) cebirin iki ana öncüsüdür. İlki, bilinmeyen doğal sayıları içeren bazı denklemleri, çözümü elde edene kadar yeni bağıntılar çıkararak çözmüştür. İkincisi ise denklemleri dönüştürmek için sistematik yöntemler ortaya koymuştur (bir terimi denklemin bir tarafından diğer tarafına taşımak gibi). Cebir terimi, ana eserinin başlığında bu yöntemlerden birini adlandırmak için kullandığı Arapça kelimeden türetilmiştir. ⓘ

Cebir, ancak François Viète'in (1540-1603) bilinmeyen veya belirtilmemiş sayıları temsil etmek için harflerin (değişkenlerin) kullanımını başlatmasıyla kendi başına bir alan haline geldi. Bu sayede matematikçiler, matematiksel formüller kullanarak temsil edilen sayılar üzerinde yapılması gereken işlemleri tanımlayabilmişlerdir. ⓘ
19. yüzyıla kadar cebir, temel olarak doğrusal denklemlerin (günümüzde doğrusal cebir) ve cebirsel denklemler olarak adlandırılan tek bilinmeyenli polinom denklemlerin (belirsiz olsa da hala kullanılan bir terim) incelenmesinden oluşuyordu. 19. yüzyıl boyunca matematikçiler, aritmetik işlemlerin genellemelerinin genellikle geçerli olduğu sayılar dışındaki şeyleri (matrisler, modüler tamsayılar ve geometrik dönüşümler gibi) temsil etmek için değişkenler kullanmaya başladılar. Cebirsel yapı kavramı, elemanları belirtilmemiş bir küme, kümenin elemanları üzerinde etkili olan işlemler ve bu işlemlerin uyması gereken kurallardan oluşan bu durumu ele alır. Bu değişim nedeniyle cebirin kapsamı, cebirsel yapıların incelenmesini de içerecek şekilde genişledi. Cebirin bu nesnesine modern cebir ya da soyut cebir adı verildi. (Bu son terim, daha çok eğitim bağlamında, formülleri manipüle etmenin eski yöntemleriyle ilgilenen temel cebire karşıt olarak kullanılmaktadır). ⓘ

Bazı cebirsel yapı türleri, matematiğin birçok alanında yararlı ve genellikle temel özelliklere sahiptir. Bunların incelenmesi cebirin özerk bölümleri haline gelmiştir ve şunları içerir:
- grup teorisi;
- alan teorisi;
- çalışmaları esasen lineer cebir ile aynı olan vektör uzayları;
- halka teorisi;
- Değişmeli halkaların incelenmesi olan değişmeli cebir, polinomların incelenmesini içerir ve cebirsel geometrinin temel bir parçasıdır;
- homolojik cebir
- Lie cebiri ve Lie grup teorisi;
- Bilgisayarların mantıksal yapısının incelenmesinde yaygın olarak kullanılan Boole cebiri. ⓘ
Matematiksel nesneler olarak cebirsel yapı türlerinin incelenmesi evrensel cebir ve kategori teorisinin konusudur. İkincisi her matematiksel yapı için geçerlidir (sadece cebirsel olanlar için değil). Başlangıçta, topolojik uzaylar gibi cebirsel olmayan nesnelerin cebirsel çalışmasına izin vermek için homolojik cebir ile birlikte tanıtılmıştır; bu özel uygulama alanı cebirsel topoloji olarak adlandırılır. ⓘ
Kalkülüs ve analiz
Önceleri sonsuz küçükler hesabı olarak adlandırılan kalkülüs, 17. yüzyıl matematikçileri Newton ve Leibniz tarafından bağımsız ve eş zamanlı olarak ortaya atılmıştır. Temelde birbirine bağlı değişkenler arasındaki ilişkinin incelenmesidir. Kalkülüs, 18. yüzyılda Euler tarafından fonksiyon kavramının ve diğer birçok sonucun ortaya atılmasıyla genişletilmiştir. Şu anda "kalkülüs" esas olarak bu teorinin temel kısmına atıfta bulunur ve "analiz" genellikle ileri kısımlar için kullanılır. ⓘ
Analiz ayrıca değişkenlerin reel sayıları temsil ettiği reel analiz ve değişkenlerin karmaşık sayıları temsil ettiği karmaşık analiz olarak alt bölümlere ayrılır. Analiz, bazılarını matematiğin diğer alanlarıyla paylaşan birçok alt alan içerir; bunlar şunları içerir:
- Çok değişkenli hesap
- Değişkenlerin değişken fonksiyonları temsil ettiği fonksiyonel analiz;
- Olasılık teorisi ile güçlü bir şekilde ilişkili olan entegrasyon, ölçü teorisi ve potansiyel teorisi;
- Adi diferansiyel denklemler;
- Kısmi diferansiyel denklemler;
- Sayısal analiz, esas olarak birçok uygulamada ortaya çıkan adi ve kısmi diferansiyel denklemlerin çözümlerinin bilgisayarlarda hesaplanmasına adanmıştır. ⓘ
Aritmetik -- Analiz -- Türev -- Kesirli hesap -- Fonksiyonlar -- Trigonometrik fonksiyonlar ⓘ
 |
 |
 |
 |

|
| Kalkülüs | Vektör hesabı | Diferansiyel denklemler | Dinamik sistem | Kaos teorisi |
Ayrık matematik
Ayrık matematik, geniş anlamda sonlu matematiksel nesnelerin incelenmesidir. Buradaki çalışma nesneleri ayrık olduğu için, kalkülüs ve matematiksel analiz yöntemleri doğrudan uygulanmaz. Algoritmalar - özellikle de bunların uygulanması ve hesaplama karmaşıklığı - ayrık matematikte önemli bir rol oynar. ⓘ
Ayrık matematik şunları içerir:
- Kombinatorik, verilen bazı kısıtlamaları karşılayan matematiksel nesneleri sıralama sanatıdır. Başlangıçta, bu nesneler belirli bir kümenin elemanları veya alt kümeleriydi; bu, kombinatorik ve ayrık matematiğin diğer bölümleri arasında güçlü bir bağlantı kuran çeşitli nesnelere genişletilmiştir. Örneğin, ayrık geometri geometrik şekillerin konfigürasyonlarının sayılmasını içerir
- Çizge teorisi ve hipergrafikler
- Hata düzeltme kodları ve kriptografinin bir bölümü de dahil olmak üzere kodlama teorisi
- Matroid teorisi
- Ayrık geometri
- Ayrık olasılık dağılımları
- Oyun teorisi (sürekli oyunlar da incelenmesine rağmen, satranç ve poker gibi en yaygın oyunlar kesikli oyunlardır)
- Kombinatoryal optimizasyon, tamsayılı programlama, kısıt programlama dahil olmak üzere ayrık optimizasyon ⓘ
Dört renk teoremi ve optimal küre paketleme, 20. yüzyılın ikinci yarısında çözülen ayrık matematiğin iki büyük problemidir. Bugüne kadar açık kalan P'ye karşı NP problemi de ayrık matematik için önemlidir, çünkü çözümü matematiğin büyük bir kısmını etkileyecektir. ⓘ
Matematiksel mantık ve küme teorisi
Matematiksel mantık ve küme teorisi konularının her ikisi de 19. yüzyılın sonlarından beri matematiğe aittir. Bu dönemden önce, kümeler matematiksel nesneler olarak görülmüyordu ve mantık, matematiksel kanıtlar için kullanılmasına rağmen, felsefeye aitti ve matematikçiler tarafından özel olarak çalışılmıyordu. ⓘ
Cantor'un sonsuz kümeler üzerine çalışmasından önce, matematikçiler aslında sonsuz koleksiyonları düşünmekte isteksizdi ve sonsuzluğu sonsuz saymanın bir sonucu olarak görüyorlardı. Cantor'un çalışması, sadece gerçekten sonsuz kümeleri dikkate alarak değil, aynı zamanda bunun farklı sonsuzluk boyutları anlamına geldiğini (bkz. Cantor'un köşegen argümanı) ve hesaplanamayan, hatta açıkça tanımlanamayan matematiksel nesnelerin varlığını (örneğin, rasyonel sayılar üzerindeki gerçek sayıların Hamel tabanları) göstererek birçok matematikçiyi rahatsız etti. Bu durum Cantor'un küme teorisi üzerine tartışmalara yol açmıştır. ⓘ
Aynı dönemde, matematiğin çeşitli alanları, temel matematiksel nesnelerin eski sezgisel tanımlarının matematiksel titizliği sağlamak için yetersiz olduğu sonucuna varmıştır. Bu tür sezgisel tanımlara örnek olarak "küme nesneler topluluğudur", "doğal sayı saymak için kullanılan şeydir", "nokta her yönde sıfır uzunluğa sahip bir şekildir", "eğri hareketli bir noktanın bıraktığı izdir" vb. verilebilir. ⓘ
Bu, matematiğin temel krizi haline geldi. Sonunda ana akım matematikte aksiyomatik yöntemin biçimselleştirilmiş bir küme teorisi içinde sistematik hale getirilmesiyle çözüldü. Kabaca söylemek gerekirse, her matematiksel nesne, tüm benzer nesnelerin kümesi ve bu nesnelerin sahip olması gereken özellikler ile tanımlanır. Örneğin, Peano aritmetiğinde doğal sayılar "sıfır bir sayıdır", "her sayının tek bir ardılı vardır", "sıfır dışındaki her sayının tek bir öncülü vardır" ve bazı akıl yürütme kuralları ile tanımlanır. Bu şekilde tanımlanan nesnelerin "doğası" matematikçilerin filozoflara bıraktığı felsefi bir sorundur, her ne kadar birçok matematikçinin bu doğa hakkında fikirleri olsa ve bu fikirlerini -bazen "sezgi" olarak adlandırılan- çalışmalarına ve ispatlarına rehberlik etmek için kullansalar da. ⓘ
Bu yaklaşım, "mantıkları" (yani izin verilen çıkarım kuralları kümelerini), teoremleri, ispatları vb. matematiksel nesneler olarak görmeye ve bunlar hakkında teoremler kanıtlamaya izin verir. Örneğin, Gödel'in eksiklik teoremleri, kabaca, doğal sayıları içeren her teoride, doğru olan (yani daha büyük bir teoride kanıtlanabilir olan), ancak teorinin içinde kanıtlanamayan teoremler olduğunu iddia eder. ⓘ
Matematiğin temellerine ilişkin bu yaklaşıma 20. yüzyılın ilk yarısında Brouwer'in başını çektiği ve dışlanmış orta yasasından açıkça yoksun olan sezgisel mantığı savunan matematikçiler tarafından karşı çıkılmıştır. ⓘ
Bu sorunlar ve tartışmalar, model teorisi (bazı mantıksal teorilerin diğer teoriler içinde modellenmesi), ispat teorisi, tip teorisi, hesaplanabilirlik teorisi ve hesaplama karmaşıklığı teorisi gibi alt alanlarla matematiksel mantığın genişlemesine yol açmıştır. Matematiksel mantığın bu yönleri bilgisayarların yükselişinden önce ortaya atılmış olsa da, derleyici tasarımı, program sertifikasyonu, ispat yardımcıları ve bilgisayar biliminin diğer yönlerinde kullanılmaları, bu mantıksal teorilerin genişlemesine katkıda bulunmuştur. ⓘ
Uygulamalı matematik
Uygulamalı matematik, bilim, mühendislik, işletme ve endüstride kullanılan matematiksel yöntemlerin incelenmesidir. Bu nedenle, "uygulamalı matematik" özel bilgi içeren bir matematik bilimidir. Uygulamalı matematik terimi aynı zamanda matematikçilerin pratik problemler üzerinde çalıştığı profesyonel uzmanlık alanını da tanımlar; pratik problemlere odaklanan bir meslek olarak uygulamalı matematik "matematiksel modellerin formülasyonu, incelenmesi ve kullanımına" odaklanır. ⓘ
Geçmişte, pratik uygulamalar matematiksel teorilerin geliştirilmesini motive etmiş, bu teoriler daha sonra matematiğin öncelikle kendi iyiliği için geliştirildiği saf matematiğin çalışma konusu haline gelmiştir. Dolayısıyla, uygulamalı matematik faaliyeti saf matematik araştırmalarıyla hayati derecede bağlantılıdır. ⓘ
İstatistik ve diğer karar bilimleri
Uygulamalı matematik, teorisi matematiksel olarak formüle edilen istatistik disiplini, özellikle de olasılık teorisi ile önemli ölçüde örtüşmektedir. İstatistikçiler (bir araştırma projesinin parçası olarak çalışan) rastgele örnekleme ve rastgele deneylerle "anlamlı veriler yaratır"; istatistiksel bir örneklemin veya deneyin tasarımı, verilerin analizini (veriler kullanılabilir hale gelmeden önce) belirler. Deneylerden ve örneklerden elde edilen verileri yeniden değerlendirirken veya gözlemsel çalışmalardan elde edilen verileri analiz ederken, istatistikçiler modelleme sanatını ve çıkarım teorisini kullanarak model seçimi ve tahmini ile "verileri anlamlandırır"; tahmin edilen modeller ve sonuç olarak ortaya çıkan tahminler yeni veriler üzerinde test edilmelidir. ⓘ
İstatistik teorisi, örneğin parametre tahmininde, hipotez testinde ve en iyiyi seçmede bir prosedür kullanmak gibi istatistiksel bir eylemin riskini (beklenen kayıp) en aza indirmek gibi karar problemlerini inceler. Matematiksel istatistiğin bu geleneksel alanlarında, bir istatistiksel karar problemi, belirli kısıtlamalar altında beklenen kayıp veya maliyet gibi bir amaç fonksiyonunun en aza indirilmesiyle formüle edilir: Örneğin, bir anketin tasarlanması genellikle bir popülasyon ortalamasının belirli bir güven düzeyiyle tahmin edilmesinin maliyetinin en aza indirilmesini içerir. Optimizasyon kullanımı nedeniyle, matematiksel istatistik teorisi, yöneylem araştırması, kontrol teorisi ve matematiksel ekonomi gibi diğer karar bilimleriyle örtüşmektedir. ⓘ
Hesaplamalı matematik
Hesaplamalı matematik, insan sayısal kapasitesi için tipik olarak çok büyük olan matematiksel problemlerin incelenmesidir. Sayısal analiz, fonksiyonel analiz ve yaklaşım teorisini kullanarak analizdeki problemler için yöntemler üzerinde çalışır; sayısal analiz genel olarak, yuvarlama hatalarına özel olarak odaklanan yaklaşım ve ayrıklaştırma çalışmalarını içerir. Sayısal analiz ve daha geniş anlamda bilimsel hesaplama, matematik biliminin analitik olmayan konularını, özellikle algoritmik-matris-ve-graf teorisini de inceler. Hesaplamalı matematiğin diğer alanları arasında bilgisayar cebiri ve sembolik hesaplama yer alır. ⓘ
Tarihçe
Matematiğin tarihi sürekli büyüyen bir soyutlamalar dizisidir. Evrimsel açıdan bakıldığında, keşfedilen ve pek çok hayvan tarafından paylaşılan ilk soyutlama muhtemelen sayılardır: örneğin, iki elma ve iki portakaldan oluşan bir koleksiyonun (diyelim ki) ortak bir yönü olduğunun, yani iki tane olduklarının farkına varılması. Kemik üzerinde bulunan çetelelerden de anlaşılacağı üzere, tarih öncesi insanlar fiziksel nesnelerin nasıl sayılacağını bilmenin yanı sıra, zaman-günler, mevsimler ya da yıllar gibi soyut niceliklerin nasıl sayılacağını da biliyor olabilirler. ⓘ

Daha karmaşık matematiğe dair kanıtlar, Babilliler ve Mısırlıların aritmetik, cebir ve geometriyi vergilendirme ve diğer mali hesaplamalar, bina ve inşaat ve astronomi için kullanmaya başladığı MÖ 3000'lere kadar ortaya çıkmaz. Mezopotamya ve Mısır'daki en eski matematiksel metinler MÖ 2000 ila 1800 yıllarına aittir. Birçok erken dönem metninde Pisagor üçlülerinden bahsedilmektedir ve bu nedenle, çıkarım yoluyla, Pisagor teoremi temel aritmetik ve geometriden sonra en eski ve yaygın matematiksel kavram gibi görünmektedir. Temel aritmetik (toplama, çıkarma, çarpma ve bölme) arkeolojik kayıtlarda ilk kez Babil matematiğinde görülür. Babilliler aynı zamanda bir yer-değer sistemine sahiptiler ve açıları ve zamanı ölçmek için bugün hala kullanılmakta olan bir seksajimal sayı sistemi kullanıyorlardı. ⓘ

MÖ 6. yüzyılda Pisagorcularla başlayan Yunan matematiği ile Antik Yunanlılar matematiği başlı başına bir konu olarak sistematik bir şekilde incelemeye başladılar. MÖ 300 civarında Öklid, bugün hala matematikte kullanılan tanım, aksiyom, teorem ve ispattan oluşan aksiyomatik yöntemi tanıttı. Elementler adlı kitabı, tüm zamanların en başarılı ve etkili ders kitabı olarak kabul edilmektedir. Antik çağın en büyük matematikçisi genellikle Siraküzalı Arşimet (MÖ 287-212) olarak kabul edilir. Dönen katı cisimlerin yüzey alanını ve hacmini hesaplamak için formüller geliştirmiş ve modern kalkülüsten çok da farklı olmayan bir şekilde, sonsuz bir serinin toplamıyla bir parabolün yayının altındaki alanı hesaplamak için tükenme yöntemini kullanmıştır. Yunan matematiğinin diğer önemli başarıları konik kesitler (Pergalı Apollonius, MÖ 3. yüzyıl), trigonometri (İznikli Hipparchus, MÖ 2. yüzyıl) ve cebirin başlangıcıdır (Diophantus, MS 3. yüzyıl). ⓘ

Bugün tüm dünyada kullanılan Hindu-Arap rakam sistemi ve işlemlerinin kullanımına ilişkin kurallar, MS birinci bin yıl boyunca Hindistan'da gelişmiş ve İslam matematiği aracılığıyla Batı dünyasına aktarılmıştır. Hint matematiğinin diğer önemli gelişmeleri arasında sinüs ve kosinüsün modern tanımı ve yaklaşımı ile sonsuz serilerin erken bir biçimi yer alır. ⓘ


İslam'ın Altın Çağı boyunca, özellikle 9. ve 10. yüzyıllarda, matematik Yunan matematiği üzerine inşa edilen birçok önemli yeniliğe sahne olmuştur. İslam matematiğinin en kayda değer başarısı cebirin geliştirilmesidir. İslami dönemin diğer başarıları arasında küresel trigonometrideki ilerlemeler ve Arap rakam sistemine ondalık noktanın eklenmesi sayılabilir. Bu dönemin Harezmî, Ömer Hayyam ve Şerafeddin Tûsî gibi pek çok önemli matematikçisi İranlıydı. ⓘ
Erken modern dönemde matematik Batı Avrupa'da hızlanarak gelişmeye başlamıştır. Isaac Newton ve Gottfried Leibniz tarafından 17. yüzyılda kalkülüsün geliştirilmesi matematikte devrim yaratmıştır. Leonhard Euler 18. yüzyılın en önemli matematikçisiydi ve çok sayıda teorem ve keşfe katkıda bulundu. Belki de 19. yüzyılın en önde gelen matematikçisi cebir, analiz, diferansiyel geometri, matris teorisi, sayı teorisi ve istatistik gibi alanlara sayısız katkıda bulunan Alman matematikçi Carl Gauss'tur. 20. yüzyılın başlarında Kurt Gödel, kısmen herhangi bir tutarlı aksiyomatik sistemin -eğer aritmetiği tanımlayacak kadar güçlüyse- kanıtlanamayan doğru önermeler içereceğini gösteren eksiklik teoremlerini yayınlayarak matematiği dönüştürdü. ⓘ
O zamandan beri matematik büyük ölçüde genişlemiş ve matematik ile bilim arasında her ikisinin de yararına olan verimli bir etkileşim olmuştur. Matematiksel keşifler günümüzde de yapılmaya devam etmektedir. Mikhail B. Sevryuk'a göre, Bulletin of the American Mathematical Society'nin Ocak 2006 sayısında, "Mathematical Reviews veritabanına 1940'tan (MR'nin ilk faaliyet yılı) bu yana dahil edilen makale ve kitap sayısı şu anda 1,9 milyondan fazladır ve veritabanına her yıl 75 binden fazla öğe eklenmektedir. Bu okyanustaki eserlerin ezici çoğunluğu yeni matematik teoremleri ve bunların ispatlarını içermektedir." ⓘ
Etimoloji
Matematik kelimesi Eski Yunanca máthēma () kelimesinden gelir ve "öğrenilen şey", "öğrenilen şey", dolayısıyla "çalışma" ve "bilim" anlamına gelir. "Matematik" kelimesi, Klasik zamanlarda bile daha dar ve daha teknik bir anlam olan "matematiksel çalışma" anlamına gelmiştir. Sıfatı mathēmatikós (), "öğrenmeyle ilgili" ya da "çalışkan" anlamına gelir ve aynı şekilde "matematiksel" anlamına da gelir. Özellikle, mathēmatikḗ tékhnē (; ) "matematiksel sanat" anlamına geliyordu. ⓘ
Benzer şekilde, Pisagorculuktaki iki ana düşünce okulundan biri mathēmatikoi (μαθηματικοί) olarak biliniyordu - o zamanlar bu modern anlamda "matematikçiler" yerine "öğrenenler" anlamına geliyordu. ⓘ
Latince'de ve 1700'lere kadar İngilizce'de matematik terimi "matematik" yerine daha çok "astroloji" (veya bazen "astronomi") anlamına geliyordu; bu anlam yaklaşık 1500'den 1800'e kadar kademeli olarak bugünkü anlamına dönüştü. Bu da çeşitli yanlış çevirilere yol açmıştır. Örneğin, Aziz Augustine'in Hıristiyanların astrologlar anlamına gelen mathematici'den sakınmaları gerektiği yönündeki uyarısı bazen matematikçilerin kınanması olarak yanlış tercüme edilmiştir. ⓘ
İngilizce'deki görünür çoğul formu, Fransızca çoğul formu (ve daha az kullanılan tekil türevi) gibi, Aristoteles (MÖ 384-322) tarafından kullanılan ve kabaca "matematiksel olan her şey" anlamına gelen Yunanca çoğul ta mathēmatiká'ya () dayanan Latince nötr çoğul formuna (Cicero) kadar uzanır, ancak İngilizce'nin yalnızca mathematic(al) sıfatını ödünç aldığı ve Yunanca'dan miras kalan fizik ve metafizik modelinden sonra matematik ismini yeniden oluşturduğu düşünülebilir. İngilizce'de matematik ismi tekil bir fiil alır. Genellikle maths ya da Kuzey Amerika'da math olarak kısaltılır. ⓘ
Önerilen tanımlar
Matematiğin tam tanımı ya da epistemolojik statüsü konusunda genel bir fikir birliği yoktur. Pek çok profesyonel matematikçi matematiğin tanımıyla ilgilenmemekte ya da matematiğin tanımlanamaz olduğunu düşünmektedir. Matematiğin bir sanat mı yoksa bir bilim mi olduğu konusunda bile bir fikir birliği yoktur. Bazıları sadece "Matematik, matematikçilerin yaptığı şeydir" demekle yetiniyor. ⓘ
Aristoteles matematiği "nicelik bilimi" olarak tanımlamış ve bu tanım 18. yüzyıla kadar geçerli olmuştur. Ancak Aristoteles sadece niceliğe odaklanmanın matematiği fizik gibi bilimlerden ayıramayacağını da belirtmiştir; ona göre soyutlama ve niceliği gerçek örneklerden "düşüncede ayrılabilir" bir özellik olarak incelemek matematiği diğerlerinden ayırır. ⓘ
19. yüzyılda matematik çalışmalarının titizliği arttığında ve grup teorisi ve projektif geometri gibi nicelik ve ölçümle net bir ilişkisi olmayan soyut konuları ele almaya başladığında, matematikçiler ve filozoflar çeşitli yeni tanımlar önermeye başladılar. Günümüzde filozoflar matematik felsefesinde matematiksel ispatın doğası gibi sorularla uğraşmaya devam etmektedir. ⓘ
Mantıksal akıl yürütme
Matematikçiler, hatalı "teoremlerden" kaçınmak için sonuçlarını sistematik bir akıl yürütme ile geliştirmeye çalışırlar. Bu yanlış ispatlar genellikle hatalı sezgilerden kaynaklanır ve matematik tarihinde yaygındır. Tümdengelimsel akıl yürütmeye izin vermek için bazı temel varsayımların aksiyomlar olarak açıkça kabul edilmesi gerekir. Geleneksel olarak bu aksiyomlar sağduyu temelinde seçilirdi, ancak modern aksiyomlar tipik olarak basit nesneler ve ilişkiler gibi ilkel kavramlar için biçimsel garantileri ifade eder. ⓘ
Matematiksel bir ispatın geçerliliği temelde bir titizlik meselesidir ve titizliğin yanlış anlaşılması matematikle ilgili bazı yaygın yanlış anlamaların önemli bir nedenidir. Matematiksel dil, veya ve sadece gibi sıradan kelimelere günlük konuşmadakinden daha fazla kesinlik kazandırabilir. Açık ve alan gibi diğer sözcüklere belirli matematiksel kavramlar için yeni anlamlar yüklenir. Bazen matematikçiler tamamen yeni sözcükler bile üretirler (örneğin homeomorfizm). Bu teknik kelime dağarcığı hem kesin hem de kompakttır ve karmaşık fikirlerin zihinsel olarak işlenmesini mümkün kılar. Matematikçiler bu dil ve mantık kesinliğine "titizlik" adını verirler. ⓘ
Matematikte beklenen titizlik zaman içinde değişmiştir: Antik Yunanlılar ayrıntılı argümanlar beklerken, Isaac Newton'un zamanında kullanılan yöntemler daha az titizdi (farklı bir matematik anlayışı nedeniyle değil, titizliğe ulaşmak için gerekli olan matematiksel yöntemlerin eksikliği nedeniyle). Newton'un yaklaşımının doğasında var olan sorunlar ancak 19. yüzyılın ikinci yarısında, reel sayıların, limitlerin ve integrallerin resmi tanımlarıyla çözülmüştür. Daha sonra, 20. yüzyılın başlarında, Bertrand Russell ve Alfred North Whitehead, tüm matematiksel kavram ve ifadelerin tanımlanabileceğini ve ardından tamamen sembolik mantık yoluyla kanıtlanabileceğini gösterme girişimi olan Principia Mathematica'yı yayınlayacaklardı. Bu, matematiği öncelikle mantığın bir uzantısı olarak gören ve mantıkçılık olarak bilinen daha geniş bir felsefi programın parçasıydı. ⓘ
Matematiğin özlü yapısına rağmen, birçok ispatın ifade edilmesi yüzlerce sayfa gerektirmektedir. Bilgisayar destekli ispatların ortaya çıkması ispat uzunluklarının daha da artmasına olanak sağlamıştır. Destekli ispatlar, ispat yazılımının kusurları varsa ve uzun, kontrol edilmesi zor ispatlarsa hatalı olabilir. Öte yandan, ispat yardımcıları elle yazılmış bir ispatta verilemeyen ayrıntıların doğrulanmasına olanak tanır ve 255 sayfalık Feit-Thompson teoremi gibi uzun ispatların doğruluğunun kesinliğini sağlar. ⓘ
Sembolik gösterim

Özel dilin yanı sıra, çağdaş matematik özel gösterimleri de yoğun bir şekilde kullanmaktadır. Bu semboller aynı zamanda hem matematiksel fikirlerin ifadesini basitleştirerek hem de tutarlı kuralları takip eden rutin işlemlere izin vererek titizliğe katkıda bulunur. Modern notasyon matematiği ustalar için çok daha verimli hale getirse de yeni başlayanlar için göz korkutucu olabilir. ⓘ
Günümüzde kullanılan matematiksel gösterimlerin çoğu, özellikle Leonhard Euler'in (1707-1783) katkılarıyla 15. yüzyıldan sonra icat edilmiştir. O zamandan önce, matematiksel argümanlar genellikle kelimelerle yazılıyordu ve bu da matematiksel keşifleri sınırlıyordu. ⓘ
19. yüzyıldan itibaren formalizm olarak bilinen bir düşünce ekolü gelişti. Bir formalist için matematik, öncelikle sembollerin biçimsel sistemleri ve bunları birleştirmeye yönelik kurallarla ilgilidir. Bu bakış açısına göre, aksiyomlar bile aksiyomatik bir sistemde, sistemdeki diğer unsurlardan prosedürel olarak türetilmeden verilen ayrıcalıklı formüllerdir. Biçimciliğin en üst örneği, David Hilbert'in 20. yüzyılın başlarında yaptığı ve genellikle Hilbert'in programı olarak adlandırılan, tüm matematiği bu şekilde kodlama çağrısıydı. ⓘ
Kurt Gödel, basit aritmetiği bile tanımlayacak kadar zengin herhangi bir biçimsel sistemin kendi tamlığını veya tutarlılığını garanti edemeyeceğini gösteren eksiklik teoremleriyle bu hedefin temelde imkansız olduğunu kanıtladı. Bununla birlikte, formalist kavramlar matematiği büyük ölçüde etkilemeye devam etmektedir, öyle ki ifadelerin varsayılan olarak küme teorisi formülleriyle ifade edilebilir olması beklenmektedir. Sadece çok istisnai sonuçların bir aksiyomatik sisteme ya da diğerine uymadığı kabul edilir. ⓘ
Soyut bilgi
Uygulamada, matematikçiler tipik olarak bilim insanlarıyla gruplandırılır ve matematiğin fiziksel bilimlerle, özellikle de varsayımlardan tümdengelim yoluyla akıl yürütme gibi pek çok ortak noktası vardır. Matematikçiler de bilim insanlarına benzer şekilde sezgileriyle deneme yanılma yöntemini kullanarak varsayım olarak bilinen matematiksel hipotezler geliştirirler. Deneysel matematik ve simülasyon gibi hesaplama yöntemlerinin de matematik içindeki önemi artmaya devam etmektedir. ⓘ
Günümüzde tüm bilimler matematikçiler tarafından incelenen problemler ortaya koymakta ve tersine, matematikten elde edilen sonuçlar genellikle bilimlerde yeni sorulara ve gerçekleşmelere yol açmaktadır. Örneğin fizikçi Richard Feynman, kuantum mekaniğinin yol integrali formülasyonunu icat etmek için matematiksel muhakeme ile fiziksel kavrayışı birleştirmiştir. Öte yandan sicim teorisi, matematikte yeni tekniklere ve sonuçlara ilham veren modern fiziğin çoğunu birleştirmek için önerilen bir çerçevedir. ⓘ

Alman matematikçi Carl Friedrich Gauss matematiği "Bilimlerin Kraliçesi" olarak adlandırmış ve daha yakın zamanlarda Marcus du Sautoy matematiği "bilimsel keşiflerin arkasındaki ana itici güç" olarak tanımlamıştır. Bununla birlikte, bazı yazarlar matematiğin modern bilim kavramından önemli bir şekilde farklı olduğunu vurgulamaktadır: matematik deneysel kanıtlara dayanmamaktadır. ⓘ
Bilimsel Devrim'den bu yana matematiksel bilginin kapsamı genişlemiş ve diğer çalışma alanlarında olduğu gibi bu da uzmanlaşmaya yol açmıştır. 2010 yılı itibariyle, Amerikan Matematik Derneği'nin en son Matematik Konu Sınıflandırması yüzlerce alt alanı tanımakta ve tam sınıflandırma 46 sayfaya ulaşmaktadır. Tipik olarak, bir alt alandaki birçok kavram matematiğin diğer dallarından süresiz olarak izole kalabilir; sonuçlar öncelikle diğer teoremleri ve teknikleri desteklemek için iskele görevi görebilir veya alt alan dışındaki herhangi bir şeyle net bir ilişkisi olmayabilir. ⓘ
Yine de matematik dikkate değer bir evrimleşme eğilimi gösterir ve zaman içinde matematikçiler genellikle şaşırtıcı uygulamalar veya kavramlar arasında bağlantılar keşfederler. Bunun çok etkili bir örneği, geometri ve cebir arasında yenilikçi ve derin bağlantılar kuran Felix Klein'ın Erlangen programıdır. Bu da her iki alanı da daha fazla soyutlamaya açmış ve tamamen yeni alt alanlar ortaya çıkarmıştır. ⓘ
Uygulamalı matematik ile saf matematik olarak bilinen, tamamen soyut sorulara ve kavramlara yönelik matematik arasında sıklıkla bir ayrım yapılır. Ancak matematiğin diğer bölümlerinde olduğu gibi bu sınır da değişkendir. Başlangıçta belirli bir uygulama göz önünde bulundurularak geliştirilen fikirler genellikle daha sonra genelleştirilir ve bunun üzerine genel matematiksel kavramlar stokuna katılır. Uygulamalı matematiğin bazı alanları, istatistik, yöneylem araştırması ve bilgisayar bilimi gibi kendi başlarına disiplinler haline gelmek için pratik alanlarla bile birleşmiştir. ⓘ
Belki de daha da şaşırtıcı olanı, fikirlerin diğer yöne doğru akması ve "en saf" matematiğin bile beklenmedik tahminlere veya uygulamalara yol açmasıdır. Örneğin, sayı teorisi modern kriptografide merkezi bir yere sahiptir ve fizikte Maxwell'in denklemlerinden türetilenler radyo dalgalarının ve ışık hızının sabitliğinin deneysel kanıtlarını önceden ortaya koymuştur. Fizikçi Eugene Wigner bu olguyu "matematiğin mantıksız etkinliği" olarak adlandırmıştır. ⓘ
Soyut matematik ile maddi gerçeklik arasındaki esrarengiz bağlantı, en azından Pisagor zamanından beri felsefi tartışmalara yol açmıştır. Antik filozof Platon bunun mümkün olduğunu çünkü maddi gerçekliğin zamanın dışında var olan soyut nesneleri yansıttığını savunmuştur. Sonuç olarak, matematiksel nesnelerin bir şekilde soyutlama içinde kendi başlarına var oldukları görüşü genellikle Platonculuk olarak adlandırılır. Çoğu matematikçi tipik olarak Platonculuğun ortaya attığı sorularla ilgilenmese de, daha felsefi düşünen bazı matematikçiler çağdaş zamanlarda bile kendilerini Platoncu olarak tanımlamaktadır. ⓘ
Yaratıcılık ve sezgi
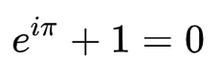
Doğruluk ve titizliğe duyulan ihtiyaç, matematiğin yaratıcılığa yer vermediği anlamına gelmez. Aksine, ezbere hesaplamaların ötesindeki çoğu matematiksel çalışma, zekice problem çözmeyi ve sezgisel olarak yeni perspektifleri keşfetmeyi gerektirir. ⓘ
Matematiksel eğilimi olanlar matematikte yalnızca yaratıcılık değil, aynı zamanda genellikle zarafet olarak tanımlanan estetik bir değer de görürler. Basitlik, simetri, bütünlük ve genellik gibi nitelikler özellikle ispatlarda ve tekniklerde değerlidir. G. H. Hardy, A Mathematician's Apology (Bir Matematikçinin Özrü) adlı eserinde, bu estetik kaygıların saf matematik çalışmalarını haklı çıkarmak için kendi başlarına yeterli olduğu inancını dile getirmiştir. Ayrıca, matematiksel estetiğe katkıda bulunan anlamlılık, beklenmediklik ve kaçınılmazlık gibi başka kriterler de tanımlamıştır. ⓘ
Paul Erdős bu düşünceyi daha ironik bir şekilde, en güzel ispatların sözde ilahi bir koleksiyonu olan "Kitap "tan bahsederek ifade etmiştir. Erdős'ten esinlenen 1998 tarihli Proofs from THE BOOK kitabı, özellikle özlü ve açıklayıcı matematiksel argümanların bir derlemesidir. Özellikle zarif sonuçlara örnek olarak Öklid'in sonsuz sayıda asal sayı olduğuna dair kanıtı ve harmonik analiz için hızlı Fourier dönüşümü verilebilir. ⓘ
Bazıları matematiği bir bilim olarak görmenin onun yedi geleneksel liberal sanat içindeki sanatını ve tarihini küçümsemek anlamına geldiğini düşünmektedir. Bu bakış açısı farklılığının ortaya çıkmasının bir yolu da matematiksel sonuçların yaratılmış mı (sanatta olduğu gibi) yoksa keşfedilmiş mi (bilimde olduğu gibi) olduğu konusundaki felsefi tartışmadır. Eğlence matematiğinin popülerliği, birçok kişinin matematiksel soruları çözmekten aldığı zevkin bir başka göstergesidir. ⓘ
20. yüzyılda matematikçi L. E. J. Brouwer, matematiği öncelikle zihindeki bazı yaratıcı süreçlerle özdeşleştiren sezgicilik olarak bilinen felsefi bir bakış açısını bile başlatmıştır. Sezgicilik de konstrüktivizm olarak bilinen ve matematiksel bir nesneyi yalnızca doğrudan inşa edilebildiği takdirde geçerli sayan, yalnızca mantık tarafından dolaylı olarak garanti edilmeyen bir duruşun bir çeşididir. Bu da kendini adamış inşacıların bazı sonuçları, özellikle de dışlanmış orta yasasına dayanan varoluşsal kanıtlar gibi argümanları reddetmelerine yol açar. ⓘ
Sonuçta, ne yapılandırmacılık ne de sezgicilik klasik matematiğin yerini almış ya da ana akım kabul görmüştür. Bununla birlikte, bu programlar sezgisel mantık ve kendi başlarına takdir edilen diğer temel anlayışlar gibi belirli gelişmeleri motive etmiştir. ⓘ
Toplum içinde
Matematik, kültürel sınırları ve zaman dilimlerini aşma konusunda dikkate değer bir yeteneğe sahiptir. Bir insan faaliyeti olarak, matematik pratiğinin eğitim, kariyer, tanınma, popülerleşme ve benzerlerini içeren sosyal bir yanı vardır. ⓘ
Ödüller ve ödül problemleri

Matematik alanındaki en prestijli ödül, 1936 yılında kurulan ve her dört yılda bir (İkinci Dünya Savaşı dönemi hariç) en fazla dört kişiye verilen Fields Madalyası'dır. Nobel Ödülünün matematiksel eşdeğeri olarak kabul edilir. ⓘ
Diğer prestijli matematik ödülleri şunlardır:
- Abel Ödülü, 2002 yılında kurulmuş ve ilk kez 2003 yılında verilmiştir
- Yaşam boyu başarı için verilen Chern Madalyası 2009 yılında tanıtıldı ve ilk kez 2010 yılında verildi
- Yine yaşam boyu başarı için verilen Wolf Matematik Ödülü 1978 yılında verilmiştir ⓘ
"Hilbert'in problemleri" olarak adlandırılan 23 açık problemden oluşan ünlü bir liste, 1900 yılında Alman matematikçi David Hilbert tarafından derlenmiştir. Bu liste matematikçiler arasında büyük bir üne kavuşmuştur ve 2022 itibariyle problemlerin en az on üçü (bazılarının nasıl yorumlandığına bağlı olarak) çözülmüştür. ⓘ
"Milenyum Ödülü Problemleri" başlıklı yedi önemli problemden oluşan yeni bir liste 2000 yılında yayımlanmıştır. Bunlardan yalnızca biri, Riemann hipotezi, Hilbert'in problemlerinden birini tekrarlamaktadır. Bu problemlerden herhangi birinin çözümü 1 milyon dolar ödül getirmektedir. Bugüne kadar bu problemlerden yalnızca biri, Poincaré varsayımı, çözülmüştür. ⓘ
Matematik eğitimi
Matematik, bilimde olduğu kadar günlük hayatta da bir insanın sık sık karşısına çıkar. Matematik, temeli mantığa dayanan bir sistemdir ve zihni geliştiren bir araç olarak kişiye rasyonel bakış açısı kazandırır. Kişiye özgür ve ön yargısız bir düşünce ortamı yaratır. İnsanın sistemli, mantıklı, tutarlı düşünmesini sağlar. Bu yüzden matematik dersi ilköğretimden yükseköğretim programlarına kadar her alanda yer alır. İlköğretimde ortaöğretime hazırlık olarak, ortaöğretimde yükseköğretime hazırlık olarak matematik öğretimi yapılır. ⓘ
Matematiğin modern kullanım alanları
- Cebirsel geometri ve teknikleri, robot ve bilgisayar oyunu modellemelerinde kullanılır.
- Diferansiyel denklemler ve sayısal analiz teknikleri uçak ve motor modellemelerinde, uydu yapımında ve daha genel olarak dinamik sistemlerin değişimlerinin ölçümünde kullanılır.
- Fraktallar, anten teknolojisinde hacmi küçük, yüzey alanı büyük antenlerin yapımında kullanılır. Ayrıca fraktal geometri, canlılarda kılcal damarların düzeni ve kanın akışının izahında kullanılır.
- Kendini kopyalayabilen makineler ve sembolik otomatlar, uzay istasyonlarından Dünya'ya gönderilen dijital verinin kaybolan parçalarının yeniden inşa edilmesinde kullanılır.
- Fourier analizi ve teknikleri, iletişim ağlarında verinin çok uzak mesafelere gönderilebilmesi ve kaybın en az olması için kullanılır. Ayrıca, Fourier teknikleri resim, video ve dijital müziğin sıkıştırılmasında kullanılır.
- Hücresel otomatlar, biyolojik canlıların üremelerini ve hastalıkların yayılmalarını modellemek için kullanılır.
- Cebirsel topolojinin bir alt dalı olan uygulamalı homoloji, dijital verinin matematiksel topolojisini belirlemek için kullanılır. Buna en iyi örnek, uzak gezegenlerin fotoğraflarından gezegen yüzeyinin coğrafyasının belirlenmesidir.
- Algoritmik teknikler programcılıkta kullanılır.
- Soyut mantık, elektrik devresi ve bilgisayar dizaynında kullanılır.
- Graf teorisi, veri tabanının topolojik ve kombinatorik olarak incelenmesinde kullanılır. Örnek olarak, bir ülkedeki hastanelerin bulundukları yer ile aralarındaki uzaklıkların ideal olup olmadığının belirlenmesini verebiliriz. Bir başka örnek ise internet sitelerinin dağılımlarının incelenmesidir. ⓘ
Matematiğin konuları
Sayılar
ⓘDoğal sayılar Tam sayılar Rasyonel sayılar İrrasyonel sayılar Reel sayılar Karmaşık sayılar Dördeyler Asal sayılar Sabitler
ⓘπ,e Hiperbolik sayılar Çifte karmaşık sayılar P-sel sayılar Ardışık sayılar Aşkın sayı Mükemmel sayı İkili sayılar Sıfır
Temel matematiksel yapılar
Monoid -- Öbek (matematik) -- Halkalar -- Cisim (Cebir) -- Topolojik Uzaylar -- Çokkatlılar -- Hilbert aksiyomları -- Sıralamalar ⓘ
Temel matematiksel kavramlar
Cebir -- Kümeler -- Sayılar -- Bağıntılar--Fonksiyonlar -- Limit -- Süreklilik -- Türev ve Türevlenebilirlik -- Analitik geometri -- İntegrallenebilirlik -- Matris --Determinantlar -- Eşyapı -- Homotopi -- İyi-sıralılık ilkesi -- Sayılabilirlik -- Soyutluk -- Oran -- Orantı -- Polinom -- Permütasyon -- Kombinasyon -- Logaritma -- Diziler -- Seriler -- Lineer cebir ⓘ
Sonlu matematik
Kombinatorik -- Saf küme teorisi -- Olasılık -- Hesap teorisi -- Sonlu matematik -- Kriptografi -- Graf teorisi -- Oyun teorisi ⓘ
ⓘ


Kombinatorik Hesap teorisi Kriptografi Graf teorisi
Uygulamalı matematik
Mekanik -- Sayısal analiz -- Optimizasyon -- Olasılık -- İstatistik -- Finansal matematik ⓘ
Ünlü teoriler ve hipotezler
Fermat'nın son teoremi -- Riemann hipotezi -- Süreklilik hipotezi -- P=NP -- Goldbach hipotezi -- Gödel'in yetersizlik teoremi -- Poincaré hipotezi -- Cantor'un diagonal yöntemi -- Pisagor teoremi -- Merkezsel limit teoremi -- Hesabın temel teoremi -- İkiz asallar hipotezi -- Cebirin temel teoremi -- Aritmetiğin temel teoremi -- Dört renk teoremi -- Zorn önsavı -- Fibonacci dizisi ⓘ
Matematik yazılımları
- Fx Draw
- Macsyma
- MAP
- Maple
- Math Type
- Mathcad
- Mathematica
- MathML
- Matlab
- Maxima
- Mupat
- GeoGebra ⓘ