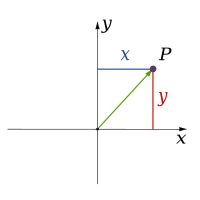Boyut
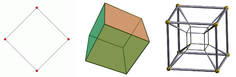

- Bir doğru parçası oluşturmak için iki nokta birleştirilebilir.
- İki paralel doğru parçası birleştirilerek bir kare oluşturulabilir.
- İki paralel kare birleştirilerek bir küp oluşturulabilir.
- İki paralel küp birleştirilerek bir tesserakt oluşturulabilir. ⓘ
| Geometri ⓘ |
|---|
 |
|
| Geometriler |
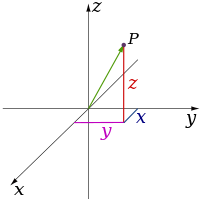
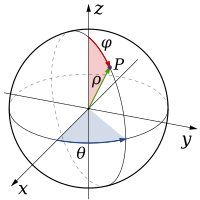
Fizik ve matematikte, matematiksel bir uzayın (veya nesnenin) boyutu, gayri resmi olarak, içindeki herhangi bir noktayı belirtmek için gereken minimum koordinat sayısı olarak tanımlanır. Dolayısıyla, bir doğrunun boyutu birdir (1D) çünkü üzerindeki bir noktayı belirtmek için yalnızca bir koordinat gerekir - örneğin, bir sayı doğrusu üzerinde 5'teki nokta. Bir silindirin veya kürenin sınırı gibi bir yüzeyin boyutu ikidir (2D) çünkü üzerindeki bir noktayı belirlemek için iki koordinat gereklidir - örneğin, bir kürenin yüzeyindeki bir noktayı bulmak için hem enlem hem de boylam gereklidir. İki boyutlu bir Öklid uzayı, düzlem üzerinde iki boyutlu bir uzaydır. Bir küpün, silindirin ya da kürenin içi üç boyutludur (3D) çünkü bu uzaylarda bir noktanın yerini belirlemek için üç koordinat gereklidir. ⓘ
Klasik mekanikte uzay ve zaman farklı kategorilerdir ve mutlak uzay ve zamana atıfta bulunur. Bu dünya anlayışı dört boyutlu bir uzaydır ancak elektromanyetizmayı tanımlamak için gerekli olan uzay değildir. Uzayzamanın dört boyutu (4D), uzamsal ve zamansal olarak mutlak bir şekilde tanımlanmayan, daha ziyade bir gözlemcinin hareketine göre bilinen olaylardan oluşur. Minkowski uzayı ilk olarak kütleçekimsiz evrene yaklaşır; genel göreliliğin sözde-Riemannian manifoldları madde ve kütleçekim ile uzayzamanı tanımlar. Süper sicim teorisini tanımlamak için 10 boyut kullanılır (6D hiperuzay + 4D), 11 boyut süperçekim ve M-teorisini tanımlayabilir (7D hiperuzay + 4D) ve kuantum mekaniğinin durum uzayı sonsuz boyutlu bir fonksiyon uzayıdır. ⓘ
Boyut kavramı fiziksel nesnelerle sınırlı değildir. Yüksek boyutlu uzaylar matematikte ve bilimlerde sıklıkla görülür. Bunlar Lagrangian veya Hamilton mekaniğinde olduğu gibi parametre uzayları veya konfigürasyon uzayları olabilir; bunlar içinde yaşadığımız fiziksel uzaydan bağımsız soyut uzaylardır. ⓘ
Boyut sayısı
|
Örnek koordinat sistemleri ⓘ | |||
|---|---|---|---|---|
| 1 |
| |||
| 2 |
| |||
| 3 |
|
Matematikte
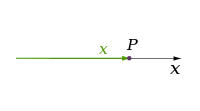
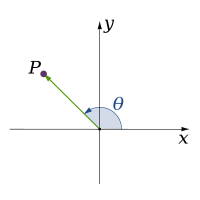
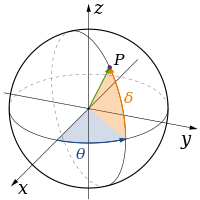
Matematikte bir nesnenin boyutu, kabaca, bu nesne üzerinde hareket eden bir noktanın serbestlik derecelerinin sayısıdır. Başka bir deyişle, boyut, nesne üzerinde olması kısıtlanan bir noktanın konumunu tanımlamak için gereken bağımsız parametrelerin veya koordinatların sayısıdır. Örneğin, bir noktanın boyutu sıfırdır; bir doğrunun boyutu birdir, çünkü bir nokta bir doğru üzerinde yalnızca bir yönde (veya tersi yönde) hareket edebilir; bir düzlemin boyutu ikidir, vb. ⓘ
Boyut, nesnenin içinde bulunduğu ya da bulunabileceği uzayın boyutundan bağımsız olması anlamında, bir nesnenin içsel bir özelliğidir. Örneğin, daire gibi bir eğrinin boyutu birdir, çünkü eğri üzerindeki bir noktanın konumu eğri üzerindeki sabit bir noktaya olan işaretli uzaklığı ile belirlenir. Bu, bir eğrinin, bir doğru olmadığı sürece, ikiden daha düşük boyutlu bir Öklid uzayına gömülemeyeceği gerçeğinden bağımsızdır. ⓘ
Öklid n-uzayı En'in boyutu n'dir. Diğer uzay türlerine genellemeye çalışırken, "En'i n-boyutlu yapan nedir?" sorusuyla karşılaşılır. Cevaplardan biri, En'deki sabit bir topu ε yarıçaplı küçük toplarla kaplamak için ε-n mertebesinde küçük toplara ihtiyaç duyulmasıdır. Bu gözlem, Minkowski boyutunun ve daha karmaşık bir varyantı olan Hausdorff boyutunun tanımlanmasına yol açar, ancak bu sorunun başka cevapları da vardır. Örneğin, En'deki bir topun sınırı yerel olarak En-1 gibi görünür ve bu da tümevarım boyutu kavramına yol açar. Bu kavramlar En üzerinde hemfikir olsa da, daha genel uzaylara bakıldığında farklı oldukları ortaya çıkar. ⓘ
Bir tesseract dört boyutlu bir nesneye örnektir. Oysa matematik dışında "boyut" teriminin kullanımı şöyledir: "Bir tesseraktın dört boyutu vardır", matematikçiler bunu genellikle şu şekilde ifade eder: "Tesseract'ın boyutu 4'tür" veya "Tesseract'ın boyutu 4'tür" veya: 4D. ⓘ
Yüksek boyut kavramı René Descartes'a kadar uzansa da, yüksek boyutlu geometrinin esaslı gelişimi ancak 19. yüzyılda Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli ve Bernhard Riemann'ın çalışmalarıyla başlamıştır. Riemann'ın 1854 tarihli Habilitationsschrift'i, Schläfli'nin 1852 tarihli Theorie der vielfachen Kontinuität'i, Hamilton'ın kuaterniyonları ve John T. Graves'in 1843'te oktoniyonları keşfi yüksek boyutlu geometrinin başlangıcını oluşturmuştur. ⓘ
Bu bölümün geri kalanında boyutun daha önemli matematiksel tanımlarından bazıları incelenmektedir. ⓘ
Vektör uzayları
Bir vektör uzayının boyutu, uzayın herhangi bir temelindeki vektörlerin sayısıdır, yani herhangi bir vektörü belirtmek için gerekli koordinat sayısıdır. Bu boyut kavramı (bir bazın kardinalitesi), diğer boyut kavramlarından ayırt etmek için genellikle Hamel boyutu veya cebirsel boyut olarak adlandırılır. ⓘ
Serbest olmayan durum için bu, bir modülün uzunluğu kavramına genelleştirilir. ⓘ
Manifoldlar
Her bağlı topolojik manifoldun tekil olarak tanımlanmış boyutu hesaplanabilir. Bağlantılı bir topolojik manifold, n sayısının manifoldun boyutu olduğu Öklid n-uzayına yerel olarak homeomorfiktir. ⓘ
Bağlantılı türevlenebilir manifoldlar için boyut aynı zamanda herhangi bir noktadaki teğet vektör uzayının boyutudur. ⓘ
Geometrik topolojide manifoldlar teorisi, 1. ve 2. boyutların nispeten basit olması, yüksek boyutlu n > 4 durumlarının "çalışılacak" fazladan alana sahip olmasıyla basitleştirilmesi ve n = 3 ve 4 durumlarının bazı açılardan en zor durumlar olmasıyla karakterize edilir. Bu durum, dört farklı ispat yönteminin uygulandığı Poincaré varsayımının çeşitli durumlarında oldukça belirgindir. ⓘ
Karmaşık boyut
Bir manifoldun boyutu, Öklid uzayının tanımlandığı temel alana bağlıdır. Analiz genellikle bir manifoldun reel sayılar üzerinde olduğunu varsaysa da, karmaşık manifoldlar ve cebirsel çeşitlerin incelenmesinde bazen bunun yerine karmaşık sayılar üzerinde çalışmak yararlı olabilir. Karmaşık bir sayı (x + iy), x ve y'nin her ikisinin de gerçel sayı olduğu bir gerçel kısım x ve bir hayali kısım y'ye sahiptir; dolayısıyla, karmaşık boyut gerçel boyutun yarısıdır. ⓘ
Tersine, cebirsel olarak kısıtlanmamış bağlamlarda, iki gerçek boyuta sahip bir nesneye tek bir karmaşık koordinat sistemi uygulanabilir. Örneğin, sıradan iki boyutlu bir küresel yüzey, karmaşık bir metrik verildiğinde, tek karmaşık boyutlu bir Riemann küresi haline gelir. ⓘ
Çeşitler
Bir cebirsel çeşitliliğin boyutu çeşitli eşdeğer yollarla tanımlanabilir. En sezgisel yol muhtemelen cebirsel bir çeşitliliğin herhangi bir Normal noktasındaki teğet uzayın boyutudur. Diğer bir sezgisel yol ise boyutu, sonlu sayıda noktaya indirgenmiş (sıfır boyut) bir çeşitlilikle kesişime sahip olmak için gereken hiper düzlem sayısı olarak tanımlamaktır. Bu tanım, bir çeşidin bir hiperdüzlemle kesişiminin, hiperdüzlem çeşidi içermediği sürece boyutu bir azalttığı gerçeğine dayanır. ⓘ
Cebirsel çeşitlerin sonlu bir birleşimi olan cebirsel bir kümenin boyutu, bileşenlerinin boyutlarının maksimumudur. Zincirlerin maksimum uzunluğuna eşittir verilen cebirsel kümenin alt çeşitlerinden oluşan bir zincirdir (böyle bir zincirin uzunluğu, ""). ⓘ
Her çeşit cebirsel bir yığın olarak düşünülebilir ve çeşit olarak boyutu yığın olarak boyutuyla aynıdır. Bununla birlikte, çeşitlere karşılık gelmeyen birçok yığın vardır ve bunlardan bazıları negatif boyuta sahiptir. Özellikle, eğer V m boyutlu bir varyete ve G V üzerine etki eden n boyutlu bir cebirsel grup ise, o zaman [V/G] bölüm yığını m - n boyutuna sahiptir. ⓘ
Krull boyutu
Bir değişmeli halkanın Krull boyutu, içindeki asal ideallerin zincirlerinin maksimum uzunluğudur, n uzunluğundaki bir zincir bir dizidir içerme ile ilişkili asal ideallerden oluşur. Cebirsel bir çeşitliliğin boyutu ile güçlü bir şekilde ilişkilidir, çünkü çeşitlilik üzerindeki polinomların halkasının alt çeşitlilikleri ve asal idealleri arasındaki doğal yazışma. ⓘ
Bir alan üzerindeki bir cebir için, vektör uzayı olarak boyut, ancak ve ancak Krull boyutu 0 ise sonludur. ⓘ
Topolojik uzaylar
Herhangi bir normal topolojik uzay X için, X'in Lebesgue örtü boyutu, aşağıdakilerin geçerli olduğu en küçük n tamsayısı olarak tanımlanır: herhangi bir açık örtü, hiçbir noktanın n + 1'den fazla elemana dahil olmadığı bir açık iyileştirmeye (her elemanın ilk örtüdeki bir elemanın alt kümesi olduğu ikinci bir açık örtü) sahiptir. Bu durumda dim X = n. Bir manifold olan X için bu, yukarıda bahsedilen boyut ile çakışır. Eğer böyle bir n tamsayısı yoksa, o zaman X'in boyutunun sonsuz olduğu söylenir ve dim X = ∞ yazılır. Dahası, X'in boyutu -1'dir, yani dim X = -1 ancak ve ancak X boş ise. Örtü boyutunun bu tanımı, normal uzaylar sınıfından tüm Tychonoff uzaylarına, sadece tanımdaki "açık" terimini "fonksiyonel olarak açık" terimiyle değiştirerek genişletilebilir. ⓘ
Tümevarımsal bir boyut tümevarımsal olarak aşağıdaki gibi tanımlanabilir. Ayrık bir nokta kümesini (sonlu bir nokta koleksiyonu gibi) 0-boyutlu olarak düşünün. 0-boyutlu bir nesne bir yönde sürüklendiğinde 1-boyutlu bir nesne elde edilir. 1 boyutlu bir nesne yeni bir yöne sürüklendiğinde 2 boyutlu bir nesne elde edilir. Genel olarak, n boyutlu bir nesneyi yeni bir yöne sürükleyerek (n + 1) boyutlu bir nesne elde edilir. Topolojik bir uzayın tümevarımsal boyutu, küçük tümevarımsal boyut veya büyük tümevarımsal boyut anlamına gelebilir ve metrik uzaylar söz konusu olduğunda, (n + 1) boyutlu topların n boyutlu sınırlara sahip olduğu analojisine dayanır ve açık kümelerin sınırlarının boyutuna dayalı tümevarımsal bir tanıma izin verir. Dahası, ayrık bir nokta kümesinin sınırı boş kümedir ve bu nedenle boş küme -1 boyutuna sahip olarak alınabilir. ⓘ
Benzer şekilde, CW kompleksleri sınıfı için, bir nesnenin boyutu, n-iskeletin önemsiz olduğu en büyük n'dir. Sezgisel olarak bu şu şekilde tanımlanabilir: orijinal uzay sürekli olarak karmaşık bir yüzeyle yüzlerinden birleştirilen daha yüksek boyutlu üçgenler koleksiyonuna deforme edilebiliyorsa, nesnenin boyutu bu üçgenlerin boyutudur. ⓘ
Hausdorff boyutu
Hausdorff boyutu, yapısal olarak karmaşık kümeleri, özellikle de fraktalları incelemek için kullanışlıdır. Hausdorff boyutu tüm metrik uzaylar için tanımlanmıştır ve yukarıda ele alınan boyutlardan farklı olarak tamsayı olmayan gerçek değerlere de sahip olabilir. Kutu boyutu veya Minkowski boyutu aynı fikrin bir çeşididir. Genel olarak, son derece düzensiz kümeler için çalışan ve tamsayı olmayan pozitif reel değerlere ulaşan daha fazla fraktal boyut tanımı vardır. ⓘ
Hilbert uzayları
Her Hilbert uzayının bir ortonormal tabanı vardır ve belirli bir uzay için bu tür iki taban aynı kardinaliteye sahiptir. Bu kardinaliteye Hilbert uzayının boyutu denir. Bu boyut, ancak ve ancak uzayın Hamel boyutu sonlu ise sonludur ve bu durumda iki boyut çakışır. ⓘ
Fizikte
Mekânsal boyutlar
Klasik fizik teorileri üç fiziksel boyutu tanımlar: uzaydaki belirli bir noktadan hareket edebileceğimiz temel yönler yukarı/aşağı, sol/sağ ve ileri/geri yönleridir. Diğer herhangi bir yöndeki hareket sadece bu üçü cinsinden ifade edilebilir. Aşağı hareket etmek, negatif bir mesafe yukarı hareket etmekle aynıdır. Çapraz olarak yukarı ve ileriye doğru hareket etmek, yönün adından da anlaşılacağı gibi, yukarı ve ilerinin doğrusal bir kombinasyonunda hareket etmektir. En basit haliyle: bir doğru bir boyutu, bir düzlem iki boyutu ve bir küp üç boyutu tanımlar. (Bkz. Uzay ve Kartezyen koordinat sistemi.) ⓘ
Sayı
boyutlar |
Örnek koordinat sistemleri ⓘ | |||
|---|---|---|---|---|
| 1 |
| |||
| 2 |
| |||
| 3 |
|
Zaman
Zamansal boyut ya da zaman boyutu, zamanın bir boyutudur. Bu nedenle zaman genellikle "dördüncü boyut" olarak adlandırılır, ancak bu onun uzamsal bir boyut olduğu anlamına gelmez. Zamansal boyut, fiziksel değişimi ölçmenin bir yoludur. Sadece bir tane olması ve zaman içinde serbestçe hareket edemeyip öznel olarak tek bir yönde hareket etmemiz nedeniyle üç uzamsal boyuttan farklı olarak algılanır. ⓘ
Fizikte gerçekliği modellemek için kullanılan denklemler, zamanı insanların yaygın olarak algıladığı şekilde ele almaz. Klasik mekaniğin denklemleri zamana göre simetriktir ve kuantum mekaniğinin denklemleri, hem zaman hem de diğer nicelikler (yük ve parite gibi) tersine çevrildiğinde tipik olarak simetriktir. Bu modellerde, zamanın tek yönde aktığı algısı termodinamik yasalarının bir eseridir (zamanı artan entropi yönünde akıyor olarak algılarız). ⓘ
Zamanın bir boyut olarak en iyi bilinen ele alınışı Poincaré ve Einstein'ın özel göreliliğidir (ve genel göreliliğe genişletilmiştir), algılanan uzay ve zamanı uzay-zaman olarak bilinen dört boyutlu bir manifoldun bileşenleri olarak ele alır ve özel, düz durumda Minkowski uzayı olarak adlandırılır. Zaman tüm uzamsal boyutlarda işlediği için diğer uzamsal boyutlardan farklıdır. Zaman birinci, ikinci ve üçüncü uzamsal boyutların yanı sıra dördüncü uzamsal boyut gibi teorik uzamsal boyutlarda da işler. Ancak zaman, geometrik bir nokta olarak tanımlanan mutlak sonsuz tekillikteki tek bir noktada mevcut değildir, çünkü sonsuz küçük bir noktada hiçbir değişiklik ve dolayısıyla zaman olamaz. Bir nesne uzaydaki konumlar arasında hareket ettiğinde olduğu gibi, zaman içindeki konumlar arasında da hareket eder. Bu anlamda herhangi bir nesneyi değişime iten güç zamandır. ⓘ
Ek boyutlar
Fizikte, üç uzay ve bir zaman boyutu kabul edilen normdur. Bununla birlikte, dört temel kuvveti ekstra boyutlar/üstuzay getirerek birleştirmeye çalışan teoriler de vardır. En önemlisi, süper sicim teorisi 10 uzay-zaman boyutu gerektirir ve geçici olarak M-teorisi olarak adlandırılan ve daha önce beş farklı süper sicim teorisini kapsayan daha temel bir 11 boyutlu teoriden kaynaklanır. Süperçekim teorisi de 11D uzayzaman = 7D hiperuzay + 4 ortak boyutu desteklemektedir. Bugüne kadar bu ekstra boyutların varlığını destekleyen doğrudan deneysel ya da gözlemsel bir kanıt mevcut değildir. Eğer hiperuzay varsa, bazı fiziksel mekanizmalar tarafından bizden gizlenmiş olmalıdır. İyi çalışılmış bir olasılık, ekstra boyutların mevcut deneyler için etkili bir şekilde görünmez olacak kadar küçük ölçeklerde "kıvrılmış" olabileceğidir. Ekstra boyutların boyut ve diğer özelliklerine ilişkin sınırlar, Büyük Hadron Çarpıştırıcısı'ndaki gibi parçacık deneyleri tarafından belirlenmektedir. ⓘ
1921 yılında Kaluza-Klein teorisi fazladan bir uzay boyutunu da içeren 5B'yi ortaya koymuştur. Kuantum alan teorisi düzeyinde Kaluza-Klein teorisi, küçük, kompakt ekstra boyutlarda yayılan yerçekiminin uzun mesafelerdeki gauge etkileşimlerine eşdeğer olduğu gerçeğine dayanarak yerçekimini gauge etkileşimleriyle birleştirir. Özellikle ekstra boyutların geometrisi önemsiz olduğunda, elektromanyetizmayı yeniden üretir. Ancak yeterince yüksek enerjilerde veya kısa mesafelerde bu düzenek, kuantum kütleçekimini tanımlamaya yönelik doğrudan girişimleri engelleyen aynı patolojilerden muzdariptir. Bu nedenle, bu modeller hala sicim teorisinin sağlamayı amaçladığı türden bir UV tamamlamasına ihtiyaç duymaktadır. Özellikle, süper sicim teorisi bir Calabi-Yau manifoldu oluşturan altı kompakt boyut (6D hiperuzay) gerektirir. Dolayısıyla Kaluza-Klein teorisi ya kendi başına eksik bir açıklama olarak ya da sicim teorisi model inşasının bir alt kümesi olarak düşünülebilir. ⓘ
Küçük ve kıvrılmış ekstra boyutlara ek olarak, görünür evrenimizle ilişkili madde (3 + 1) boyutlu bir alt uzayda lokalize olduğu için görünmeyen ekstra boyutlar da olabilir. Bu nedenle ekstra boyutların küçük ve kompakt olması gerekmez, ancak büyük ekstra boyutlar olabilir. D-branlar, sicim teorisi tarafından öngörülen ve bu rolü oynayabilecek çeşitli boyutlardaki dinamik genişletilmiş nesnelerdir. Gösterge etkileşimleriyle ilişkili olan açık sicim uyarımlarının uç noktaları tarafından zarla sınırlandırılması özelliğine sahipken, kütleçekim etkileşimine aracılık eden kapalı sicimler tüm uzayzamana veya "kütleye" yayılmakta serbesttir. Bu durum kütleçekiminin neden diğer kuvvetlerden katlanarak daha zayıf olduğuyla ilgili olabilir, çünkü daha yüksek boyutlu bir hacme yayıldıkça kendini etkili bir şekilde seyreltir. ⓘ
Brane fiziğinin bazı yönleri kozmolojiye uygulanmıştır. Örneğin, brane gazı kozmolojisi topolojik ve termodinamik düşünceleri kullanarak uzayın neden üç boyutu olduğunu açıklamaya çalışır. Bu düşünceye göre üç boyut, sicimlerin genel olarak kesişebileceği en büyük uzamsal boyut sayısıdır. Başlangıçta kompakt boyutlar etrafında çok sayıda sicim sarımı varsa, uzay ancak bu sarımlar ortadan kaldırıldığında makroskopik boyutlara genişleyebilir, bu da zıt sarımlı sicimlerin birbirini bulmasını ve yok olmasını gerektirir. Ancak sicimler sadece üç boyutta anlamlı bir oranda yok olmak için birbirlerini bulabilir, bu nedenle bu tür bir başlangıç konfigürasyonu göz önüne alındığında uzayın sadece üç boyutunun büyümesine izin verilir. ⓘ
Eğer tüm alanlar içlerinde yayılmakta eşit derecede özgürse, ekstra boyutların evrensel olduğu söylenir. ⓘ
Aralık 2012'de Büyük Hadron Çarpıştırıcısı sonuçlarının analizi, büyük ilave boyutlu teorileri ciddî şekilde sınırlamıştır. ⓘ
Uzaya ilave boyutlar eklemiş başka fizîki teorilerse şunlardır:
- Kaluza–Klein teorisi, kütleçekimi dışındaki kuvvetleri açıklamak için ilave boyutlar getirir (aslen sadece elektromanyetizma).
- Büyük ilave boyutlar ve Randall–Sundrum Modeli, kütleçekimin zaafını açıklamaya çalışır. Bu özellik brane kozmolojisinde kullanılır.
- Evrensel ilave boyutlar ⓘ
Bilgisayar grafikleri ve uzamsal verilerde
İllüstrasyon yazılımı, Bilgisayar destekli tasarım ve Coğrafi bilgi sistemleri de dahil olmak üzere çeşitli dijital sistem türleri geometrik şekillerin depolanması, analizi ve görselleştirilmesine dayanmaktadır. Farklı vektör sistemleri şekilleri temsil etmek için çok çeşitli veri yapıları kullanır, ancak neredeyse hepsi temelde uzamsal boyutlara karşılık gelen bir dizi geometrik ilkel öğeye dayanır:
- Nokta (0 boyutlu), Kartezyen koordinat sisteminde tek bir koordinat.
- Çizgi veya Çoklu Çizgi (1 boyutlu), genellikle sürekli bir çizgiden örneklenen noktaların sıralı bir listesi olarak temsil edilir, bunun üzerine yazılımın çizginin aradaki şeklini düz veya eğri çizgi parçaları olarak enterpole etmesi beklenir.
- Çokgen (2 boyutlu), genellikle uç noktalarında kapanan ve iki boyutlu bir bölgenin sınırını temsil eden bir çizgi olarak temsil edilir. Yazılımın bu sınırı 2 boyutlu uzayı iç ve dış olarak bölmek için kullanması beklenir.
- Yüzey (3 boyutlu), bağlı çokgen yüzlerden oluşan bir çokyüzlü gibi çeşitli stratejiler kullanılarak temsil edilir. Yazılımın bu yüzeyi 3 boyutlu uzayı iç ve dış olarak bölmek için kullanması beklenir. ⓘ
Bu sistemlerde, özellikle CBS ve Haritacılıkta, gerçek dünyadaki bir olgunun temsili, temsil edilen olgudan farklı (genellikle daha düşük) bir boyuta sahip olabilir. Örneğin, bir şehir (iki boyutlu bir bölge) bir nokta olarak ya da bir yol (üç boyutlu bir malzeme hacmi) bir çizgi olarak temsil edilebilir. Bu boyutsal genelleme, uzamsal bilişteki eğilimlerle ilişkilidir. Örneğin, iki şehir arasındaki mesafeyi sormak, şehirlerin nokta olarak kavramsal bir modelini varsayarken, "yukarı", "aşağı" veya "bir yol boyunca" seyahat etmeyi içeren yönergeler vermek tek boyutlu bir kavramsal model anlamına gelir. Bu genellikle veri verimliliği, görsel basitlik veya bilişsel verimlilik amacıyla yapılır ve temsil ile temsil edilen arasındaki ayrım anlaşılırsa kabul edilebilir, ancak bilgi kullanıcıları dijital şeklin gerçekliğin mükemmel bir temsili olduğunu varsayarsa (örneğin, yolların gerçekten çizgi olduğuna inanmak) kafa karışıklığına neden olabilir. ⓘ
Literatürde
Bilim kurgu metinlerinde paralel veya alternatif evrenlere ya da diğer hayali varoluş düzlemlerine atıfta bulunulurken sıklıkla "boyut" kavramından bahsedilir. Bu kullanım, paralel/alternatif evrenlere/düzlemlere seyahat etmek için standart olanın dışında bir yönde/boyutta seyahat etmek gerektiği fikrinden türetilmiştir. Gerçekte, diğer evrenler/düzlemler bizimkinden sadece küçük bir mesafe uzaklıktadır, ancak bu mesafe standart boyutlarda değil, dördüncü (veya daha yüksek) bir uzamsal (veya uzamsal olmayan) boyuttadır. ⓘ
Gerçek geometrik boyutlulukla ilgili en çok müjdelenen bilim kurgu öykülerinden biri ve bu tür konuları araştırmaya yeni başlayanlar için genellikle bir başlangıç noktası olarak tavsiye edilen, Edwin A. Abbott'un 1884 tarihli romanı Flatland'dir. Isaac Asimov, 1984 tarihli Signet Classics baskısına yazdığı önsözde Flatland'i "Boyutları algılama biçimine dair bulunabilecek en iyi giriş" olarak tanımlamıştır. ⓘ
Diğer boyutlar fikri, örneğin Miles J. Breuer'in The Appendix and the Spectacles (1928) ve Murray Leinster'in The Fifth-Dimension Catapult (1931) adlı kitaplarında öne çıkan birçok erken dönem bilim kurgu öyküsüne dahil edilmiş ve 1940'lara kadar bilim kurguda düzensiz olarak yer almıştır. Diğer boyutları içeren klasik öyküler arasında Robert A. Heinlein'ın -And He Built a Crooked House (1941), Kaliforniyalı bir mimarın bir tesseract'ın üç boyutlu bir projeksiyonuna dayanan bir ev tasarladığı; Alan E. Nourse'un Tiger by the Tail ve The Universe Between (her ikisi de 1951); ve Walter Tevis'in The Ifth of Oofth (1957) adlı kitapları sayılabilir. Bir başka referans da Madeleine L'Engle'ın A Wrinkle In Time (1962) adlı romanıdır; bu romanda beşinci boyut "evreni tesseract etmek" ya da uzayı hızlı bir şekilde katlamak için bir yol olarak kullanılmıştır. Dördüncü ve beşinci boyutlar aynı zamanda William Sleator'un The Boy Who Reversed Himself adlı kitabının da önemli bir bileşenidir. ⓘ
Felsefede
Immanuel Kant 1783'te şöyle yazmıştır: "Uzayın (kendisi başka bir uzayın sınırı olmayan) her yerde üç boyuta sahip olduğu ve genel olarak uzayın daha fazla boyuta sahip olamayacağı, bir noktada üçten fazla doğrunun dik açıyla kesişemeyeceği önermesine dayanır. Bu önerme kavramlardan hareketle gösterilemez, ancak doğrudan sezgiye ve hatta apodiktik (kanıtlanabilir) olarak kesin olduğu için a priori saf sezgiye dayanır." ⓘ
"Uzayın Dört Boyutu Vardır", Alman filozof ve deneysel psikolog Gustav Fechner tarafından 1846 yılında "Dr. Mises" takma adıyla yayınlanan kısa bir öyküdür. Öykünün kahramanı, diğer gölgelerin farkında olan ve onlarla iletişim kurabilen, ancak iki boyutlu bir yüzeye hapsolmuş bir gölgedir. Fechner'e göre bu "gölge adam" üçüncü boyutu zaman olarak algılamaktadır. Hikaye, Platon'un Cumhuriyet (M.Ö. 380) adlı eserinde yer alan "Mağara Alegorisi" ile güçlü bir benzerlik taşımaktadır. ⓘ
Simon Newcomb 1898 yılında Bulletin of the American Mathematical Society için "The Philosophy of Hyperspace" başlıklı bir makale yazmıştır. Linda Dalrymple Henderson, yirminci yüzyıl başı sanatında dördüncü boyut hakkındaki 1983 tarihli tezinde, metafizik temaları keşfetmek için daha yüksek boyutları kullanan yazıları tanımlamak için kullanılan "hiperuzay felsefesi" terimini ortaya atmıştır. "Hiperuzay filozoflarına" örnek olarak 1888 yılında "tesseract" kelimesini kullanan ilk yazar olan Charles Howard Hinton ve Rus ezoterist P. D. Ouspensky verilebilir. ⓘ
Daha fazla boyut
| Geometri ⓘ |
|---|
 |
|
| Geometriler |
- Serbestlik derecesi
- mekanikte
- fizik ve kimya alanlarında
- istatistikte
- Dış boyut
- Hurst üsteli
- İzoperimetrik boyut
- Metrik boyut
- Sipariş boyutu
- q-boyutu
- Fraktal (q = 1)
- Korelasyon (q = 2) ⓘ
Konuyla ilgili yayınlar
- Edwin A. Abbott, (1884) Flatland: A Romance of Many Dimensions, Public Domain. Online version with ASCII approximation of illustrations 24 Eylül 2009 tarihinde Wayback Machine sitesinde arşivlendi. at Project Gutenberg.
- Thomas Banchoff, (1996) Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, Second Edition, Freeman.
- Clifford A. Pickover, (1999) Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons, Oxford University Press.
- Rudy Rucker, (1984) The Fourth Dimension, Houghton-Mifflin.
- Michio Kaku, (1994) Hyperspace, a Scientific Odyssey Through the 10th Dimension, Oxford University Press. ⓘ
| Fizik ile ilgili bu madde taslak seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. ⓘ |
| Matematik ile ilgili bu madde taslak seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. ⓘ |