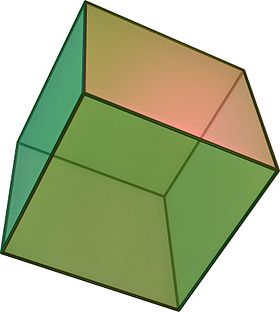
Küp

Düzenli altı yüzlü ⓘ
(Dönen model için buraya tıklayın)
Tip	Platonik katı
kısa kod	4=
Elementler	F = 6, E = 12 V = 8 (χ = 2)
Yan yana yüzler	6{4}
Conway notasyonu	C
Schläfli sembolleri	{4,3}
	t{2,4} veya {4}×{} tr{2,2} veya {}×{}×{}
Yüz yapılandırması	V3.3.3.3
Wythoff sembolü	2 4
Coxeter diyagramı
Simetri	Oh, B3, [4,3], (*432)
Rotasyon grubu	O, [4,3]+, (432)
Referanslar	U06, C18, W3
Özellikler	düzenli, konvekszonohedron
Dihedral açı	90°
4.4.4 (Vertex figürü)	Oktahedron (çift polihedron)
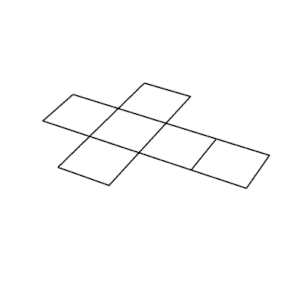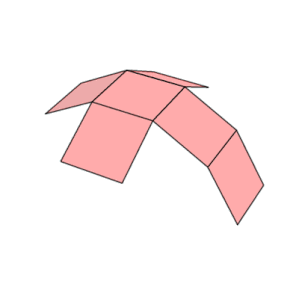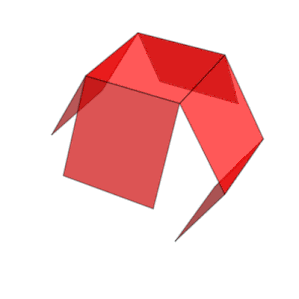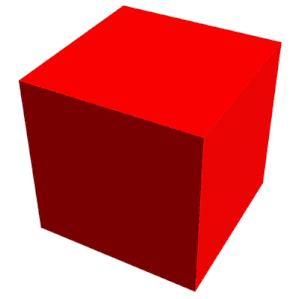
Net

Bir küpün ağı ⓘ

Geometride küp, altı kare yüz, faset veya kenar ile sınırlandırılmış, her bir tepe noktasında üçü buluşan üç boyutlu katı bir nesnedir. ⓘ

Küp tek düzenli altı yüzlüdür ve beş Platonik katıdan biridir. 6 yüzü, 12 kenarı ve 8 köşesi vardır. ⓘ

Küp aynı zamanda bir kare paralel yüzlü, bir eşkenar küboid ve bir sağ eşkenar dörtgen, bir 3-zonohedrondur. Üç yönde düzenli bir kare prizma ve dört yönde bir trigonal trapezohedrondur. ⓘ

Küp, oktahedronun çiftidir. Kübik veya oktahedral simetriye sahiptir. ⓘ

Küp, tüm yüzleri kare olan tek dışbükey çokyüzlüdür. ⓘ

Şeffaf olan ve yavaş yavaş dönen bir küp		Bir küp ilüstrasyonu; yapısını vurgulamak için dört farklı yöntem kullanılmıştır: çevirme, katlanma/katlanmama, yarı şeffaflık ve en önemlisi stereogram. (Animasyonu izle)

Ortogonal projeksiyonlar

Küpün bir tepe noktasında, kenarlarında, yüzünde ve tepe noktasına göre normalinde ortalanmış dört özel ortogonal izdüşümü vardır. Birinci ve üçüncü, A₂ ve B₂ Coxeter düzlemlerine karşılık gelir. ⓘ

Ortogonal izdüşümler ⓘ

Merkezinde	Yüz	Vertex
Coxeter düzlemleri	B2	A2
Projektif simetri	[4]	[6]
Eğik görünümler

Küresel döşeme

Küp aynı zamanda küresel bir döşeme olarak da temsil edilebilir ve stereografik bir projeksiyonla düzleme yansıtılabilir. Bu izdüşüm konformaldir, açıları korur ancak alanları veya uzunlukları korumaz. Küre üzerindeki düz çizgiler düzlem üzerinde dairesel yaylar olarak yansıtılır. ⓘ

Ortografik projeksiyon	Stereografik projeksiyon

Kartezyen koordinatlar

Orijin merkezli, kenarları eksenlere paralel ve kenar uzunluğu 2 olan bir küp için köşelerin Kartezyen koordinatları şöyledir

(±1, ±1, ±1) ⓘ

iç kısım ise tüm i için -₁ < xi < 1 olan tüm noktalardan (x₀, x1, x₂) oluşur. ⓘ

İçindeki denklem (math)

Analitik geometride, merkezi (x₀, y₀, z₀) ve kenar uzunluğu 2a olan bir küpün yüzeyi, aşağıdaki gibi tüm noktaların (x, y, z) yeridir

$\max\{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|\}=a.$ ⓘ

Bir küp, üç üs de sonsuza yaklaştıkça 3D süperelipsoidin sınırlayıcı durumu olarak da düşünülebilir. ⓘ

Formüller

Kenar uzunluğu olan bir küp için $a$:

yüzey alanı	$6a^{2}\,$	hacim	$a^{3}\,$ ⓘ
yüz diyagonal	${\sqrt {2}}a$	uzay köşegeni	${\textstyle {\sqrt {3}}a}$
çevrelenmiş kürenin yarıçapı	${\frac {\sqrt {3}}{2}}a$	kenarlara teğet küre yarıçapı	${\frac {a}{\sqrt {2}}}$
yazılı kürenin yarıçapı	${\frac {a}{2}}$	yüzeyler arasındaki açılar (radyan cinsinden)	${\frac {\pi }{2}}$

Bir küpün hacmi, kenarlarının üçüncü kuvveti olduğundan $a\times a\times a$üçüncü kuvvetler, kareler ve ikinci kuvvetlere benzer şekilde küp olarak adlandırılır. ⓘ

Bir küp, belirli bir yüzey alanına sahip küboidler (dikdörtgen kutular) arasında en büyük hacme sahiptir. Ayrıca, bir küp aynı toplam doğrusal boyuta (uzunluk+genişlik+yükseklik) sahip küpler arasında en büyük hacme sahiptir. ⓘ

Uzayda nokta

Çevreleyen küresi R yarıçapına sahip bir küp için ve küpün sekiz köşesinden di uzaklıklarına sahip 3 boyutlu uzayında verilen bir nokta için:

${\frac {\sum _{i=1}^{8}d_{i}^{4}}{8}}+{\frac {16R^{4}}{9}}=\left({\frac {\sum _{i=1}^{8}d_{i}^{2}}{8}}+{\frac {2R^{2}}{3}}\right)^{2}.$ ⓘ

Küpün iki katına çıkarılması

Küpün iki katına çıkarılması ya da Delian problemi, Antik Yunan matematikçilerinin sadece bir pergel ve çizgeç kullanarak belirli bir küpün kenar uzunluğundan başlayıp orijinal küpün iki katı hacme sahip bir küpün kenar uzunluğunu inşa etme problemiydi. Bu problemi çözemediler ve 1837'de Pierre Wantzel bunun imkansız olduğunu kanıtladı çünkü 2'nin küp kökü inşa edilebilir bir sayı değildir. ⓘ

Düzgün renklendirmeler ve simetri

Oktahedral simetri ağacı ⓘ

Küp, her bir tepe noktasının etrafındaki kare yüzlerin renkleriyle adlandırılan üç tek tip renklendirmeye sahiptir: 111, 112, 123. ⓘ

Küpün dört simetri sınıfı vardır ve bunlar yüzlerin tepe-geçişli renklendirilmesiyle temsil edilebilir. En yüksek oktahedral simetri olan Oh'un tüm yüzleri aynı renktedir. D_4h dihedral simetrisi küpün bir katı olmasından kaynaklanır ve altı yüzün hepsi farklı renktedir. Prizmatik alt kümeler D_2d bir öncekiyle aynı renge sahiptir ve D_2h, zıt kenarlarla eşleştirilmiş toplam üç renk için kenarları için alternatif renklere sahiptir. Her simetri formunun farklı bir Wythoff sembolü vardır. ⓘ

İsim	Düzenli hexahedron	Kare prizma	Dikdörtgen trapezoprizm	Dikdörtgen küboid	Rhombic prizma	Trigonal trapez yüzlü ⓘ
Coxeter diyagramı
Schläfli sembolü	{4,3}	{4}×{ } rr{4,2}	s2{2,4}	{ }3 tr{2,2}	{ }×2{ }
Wythoff sembolü	4 2	2
Simetri	Oh [4,3] (*432)	D4h [4,2] (*422)	D2d [4,2+] (2*2)	D2h [2,2] (*222)		D3d [6,2+] (2*3)
Simetri Sipariş	24	16	8	8		12
Resim (üniforma renklendirme)	(111)	(112)	(112)	(123)	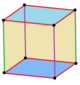(112)	(111), (112)

Geometrik ilişkiler

Küpün 11 ağı. ⓘ

Bu tanıdık altı yüzlü zarlar küp şeklindedir. ⓘ

Bir küpün on bir ağı vardır (biri yukarıda gösterilmiştir): yani, içi boş bir küpü yedi kenarını keserek düzleştirmenin on bir yolu vardır. Küpü, bitişik iki yüz aynı renge sahip olmayacak şekilde renklendirmek için en az üç renge ihtiyaç vardır. ⓘ

Küp, üç boyutlu Öklid uzayının tek düzenli döşemesinin hücresidir. Ayrıca Platonik katılar arasında çift sayıda kenara sahip yüzlere sahip olmasıyla benzersizdir ve sonuç olarak bu grubun zonohedron olan tek üyesidir (her yüz nokta simetrisine sahiptir). ⓘ

Küp altı özdeş kare piramide kesilebilir. Bu kare piramitler daha sonra ikinci bir küpün yüzlerine eklenirse, eşkenar dörtgen bir dodekahedron elde edilir (eşkenar üçgen çiftleri eşkenar dörtgen yüzler halinde birleştirilir). ⓘ

Diğer boyutlar

Dört boyutlu Öklid uzayında bir küpün benzerinin özel bir adı vardır: tesserakt veya hiperküp. Daha doğru bir ifadeyle, hiperküp (veya n-boyutlu küp veya sadece n-küp) küpün n-boyutlu Öklid uzayındaki analogudur ve tesserakt da 4. dereceden hiperküptür. Bir hiperküp aynı zamanda bir ölçü politopu olarak da adlandırılır. ⓘ

Küpün daha düşük boyutlarda da benzerleri vardır: 0 boyutunda bir nokta, bir boyutta bir doğru parçası ve iki boyutta bir kare. ⓘ

İlgili polihedralar

Bir küpün ikizi, burada köşeleri küpün kare yüzlerinin merkezinde görülen bir oktahedrondur. ⓘ

Hemiküp, küpün 2'ye 1 bölümüdür. ⓘ

Küpün antipodal harita ile bölümü projektif bir çokyüzlü olan hemiküpü verir. ⓘ

Orijinal küpün kenar uzunluğu 1 ise, çift çokyüzlünün (bir oktahedron) kenar uzunluğu $\scriptstyle {\sqrt {2}}/2$. ⓘ

Küp, genel çokyüzlülerin çeşitli sınıflarında özel bir durumdur:

İsim	Eşit kenar uzunlukları?	Eşit açılar?	Dik açılar? ⓘ
Küp	Evet	Evet	Evet
Rhombohedron	Evet	Evet	Hayır
Kübik	Hayır	Evet	Evet
Parallelepiped	Hayır	Evet	Hayır
dörtgen yüzlü altı yüzlü	Hayır	Hayır	Hayır

Bir küpün köşeleri, her biri düzenli bir dörtyüzlü oluşturan dörderli iki grup halinde gruplandırılabilir; daha genel olarak buna demiküp denir. Bu ikisi birlikte düzenli bir bileşik olan stella octangula'yı oluşturur. İkisinin kesişimi düzenli bir oktahedron oluşturur. Düzenli bir dörtyüzlünün simetrileri, her bir dörtyüzlüyü kendisine eşleyen bir küpün simetrilerine karşılık gelir; küpün diğer simetrileri ise ikisini birbirine eşler. ⓘ

Böyle bir düzgün dörtyüzlü, küpün 1/3'ü kadar bir hacme sahiptir. Geriye kalan alan, her biri küpün 1/6'sı kadar hacme sahip dört eşit düzensiz dörtyüzlüden oluşur. ⓘ

Düzeltilmiş küp, küboktahedrondur. Daha küçük köşeler kesilirse altı sekizgen yüzlü ve sekiz üçgen yüzlü bir çokyüzlü elde ederiz. Özellikle düzenli sekizgenler (kesik küp) elde edebiliriz. Rhombicuboctahedron, hem köşelerin hem de kenarların doğru miktarda kesilmesiyle elde edilir. ⓘ

Bir küp bir dodekahedronun içine yerleştirilebilir, böylece küpün her bir köşesi dodekahedronun bir köşesi olur ve her bir kenar dodekahedronun yüzlerinden birinin köşegeni olur; bu tür tüm küpleri almak düzenli beş küp bileşiğini ortaya çıkarır. ⓘ

Bir küpün karşılıklı iki köşesi, kendilerine doğrudan bağlı üç köşenin derinliğinde kesilirse, düzensiz bir oktahedron elde edilir. Bu düzensiz oktahedraların sekizi, küboktahedronu elde etmek için düzenli bir oktahedronun üçgen yüzlerine eklenebilir. ⓘ

Küp, topolojik olarak bir dizi küresel çok yüzlü ve 3. dereceden tepe figürlü tilinglerle ilişkilidir. ⓘ

Düzenli tilinglerin *n32 simetri mutasyonu: {n,3}
Küresel				Öklid	Kompakt hiperb.		Paraco.	Kompakt olmayan hiperbolik
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Küboktahedron, küp ve düzgün oktahedron ile ilişkili bir düzgün çokyüzlü ailesinden biridir. ⓘ

Düzgün oktahedral çokyüzlüler ⓘ
Simetri: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= veya	= veya	=
Düzgün polihedraların dualleri
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Küp, topolojik olarak hiperbolik düzleme uzanan düzenli tilings dizisinin bir parçası olarak ilişkilidir: {4,p}, p=3,4,5... ⓘ

Düzenli eğimlerin *n42 simetri mutasyonu: {4,n}
Küresel	Öklid	Kompakt hiperbolik				Paracompact
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}...	{4,∞}

Dihedral simetri, Dih₄ ile küp, hiperbolik düzleme uzanan bir dizi düzgün çok yüzlü ve 4.2n.2n tilings ile topolojik olarak ilişkilidir:

*n42 kesilmiş tilinglerin simetri mutasyonu: 4.2n.2n
Simetri *n42 [n,4]	Küresel		Öklid	Kompakt hiperbolik				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Kesilmiş rakamlar
Konfigürasyon.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
n-kis rakamlar
Konfigürasyon.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Tüm bu şekiller oktahedral simetriye sahiptir. ⓘ

Küp, [n,3] Coxeter grup simetrisine sahip eşkenar dörtgen çokyüzlüler ve tilingler dizisinin bir parçasıdır. Küp, eşkenar dörtgenlerin kare olduğu eşkenar dörtgen bir altı yüzlü olarak görülebilir. ⓘ

Dual quasiregular tilinglerin simetri mutasyonları: V(3.n)2 ⓘ
*n32	Küresel			Öklid	Hiperbolik
	*332	*432	*532	*632	*732	*832...	*∞32
Döşeme
Konf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

Küp bir kare prizmadır:

Düzgün n-gonal prizmalar ailesi
Prizma adı	Digonal prizma	(Trigonal) Üçgen prizma	(Tetragonal) Kare prizma	Beşgen prizma	Altıgen prizma	Heptagonal prizma	Sekizgen prizma	Enneagonal prizma	Ongen prizma	Hendecagonal prizma	Onikigen prizma	...	Apeirogonal prizma
Polihedron görüntüsü												...
Küresel döşeme görüntüsü												Düzlem döşeme görüntüsü
Tepe konfigürasyonu.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diyagramı												...

Bir trigonal trapezohedron olarak küp, altıgen dihedral simetri ailesiyle ilişkilidir. ⓘ

Düzgün altıgen dihedral küresel çokyüzlüler ⓘ
Simetri: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
İkili üniformalar
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Düzenli ve düzgün küp bileşikleri ⓘ

Üç küpün bileşimi

Beş küpten oluşan bileşik

Tek tip peteklerde ve polikoralarda

28 dışbükey düzgün petekten 9'unun bir elemanıdır: ⓘ

Kübik petek	Kesik kare prizmatik bal peteği	Saplı kare prizmatik petek	Uzatılmış üçgen prizmatik bal peteği	Jiroelongasyonlu üçgen prizmatik bal peteği ⓘ
Kantellenmiş kübik petek	Cantitruncated kübik bal peteği	Runcitruncated kübik petek	Runcinated dönüşümlü kübik petek

Aynı zamanda beş adet dört boyutlu tekdüze polikoranın bir unsurudur: ⓘ

Tesseract	Kantellenmiş 16 hücreli	Runcinated tesseract	Cantitruncated 16-hücre	Runcitruncated 16 hücreli

Kübik grafik

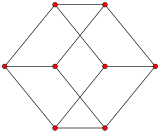
Kübik grafik ⓘ
Adını	Q3
Köşeler	8
Kenarlar	12
Yarıçap	3
Çap	3
Çevresi	4
Otomorfizmler	48
Kromatik sayı	2
Özellikler	Hamiltonyen, düzenli, simetrik, mesafeli-düzenli, mesafeli-geçişli, 3 köşeli-bağlantılı, iki parçalı, düzlemsel çizge
Grafikler ve parametreler tablosu

Küpün iskeleti (köşeler ve kenarlar), küp grafiği olarak adlandırılan 8 köşeli ve 12 kenarlı bir grafik oluşturur. Bu, hiperküp grafiğinin özel bir durumudur. Her biri kendi Platonik katısının iskeleti olan 5 Platonik çizgeden biridir. ⓘ

Bir uzantısı, k = 2 için küp grafiği olan üç boyutlu k-ARY Hamming grafiğidir. Bu tür graflar bilgisayarlarda paralel işlem teorisinde ortaya çıkar. ⓘ