Kare

Kare ⓘ
Kare ⓘ
	Düzgün bir dörtgen
Tip	Düzenli çokgen
Kenarlar ve köşeler	4
Schläfli sembolü	{4}
Coxeter-Dynkin diyagramları	;
Simetri grubu	Dihedral (D4), sıra 2×4
İç açı (derece)	90°
Mülkler	Dışbükey, döngüsel, eşkenar, izogonal, izotoksal

Kare ⓘ

Cetvel ve pergel kullanarak kare çizimi ⓘ

Kare, bütün kenarları ve açıları birbirine eşit olan düzgün dörtgendir. Matematiğin en temel geometrik şekilleri arasındadır. Aynı zamanda dikdörtgendir ve eşkenar dörtgendir. Bu iki özel dörtgenin tüm özelliklerini taşır. Eski adı ise murabbadır. ⓘ

Karakterizasyonlar

Dışbükey bir dörtgen, ancak ve ancak aşağıdakilerden herhangi biri ise bir karedir:

İki bitişik eşit kenarı olan bir dikdörtgen
Dik tepe açısına sahip bir eşkenar dörtgen
Tüm açıları eşit olan bir eşkenar dörtgen
Bir dik tepe açısı ve iki bitişik eşit kenarı olan bir paralelkenar
Dört eşit kenarı ve dört dik açısı olan bir dörtgen
Köşegenlerin eşit olduğu ve birbirlerinin dik açıortayları olduğu bir dörtgen (yani, eşit köşegenlere sahip bir eşkenar dörtgen)
Ardışık kenarları a, b, c, d olan dışbükey bir dörtgenin alanı $A={\tfrac {1}{2}}(a^{2}+c^{2})={\tfrac {1}{2}}(b^{2}+d^{2}).$ ⓘ

Mülkler

Kare, eşkenar dörtgen (eşit kenarlar, karşılıklı eşit açılar), uçurtma (iki çift bitişik eşit kenar), yamuk (bir çift karşılıklı kenar paralel), paralelkenar (tüm karşılıklı kenarlar paralel), dörtgen veya dörtgen (dört kenarlı çokgen) ve dikdörtgenin (karşılıklı kenarlar eşit, dik açılar) özel bir durumudur ve bu nedenle tüm bu şekillerin tüm özelliklerine sahiptir:

Bir karenin dört iç açısı da eşittir (her biri 360°/4 = 90°, bir dik açıdır).
Bir karenin merkez açısı 90°'ye eşittir (360°/4).
Bir karenin dış açısı 90°'ye eşittir.
Bir karenin köşegenleri eşittir ve 90°'de buluşarak birbirlerini keserler.
Bir karenin köşegeni iç açısını ikiye böler ve 45°'lik bitişik açılar oluşturur.
Bir karenin dört kenarı da eşittir.
Bir karenin karşıt kenarları paraleldir.
Kare, n-hiperküp ve n-ortopleks ailelerinin n=2 durumudur.
Bir karenin Schläfli sembolü {4}'tür. Kesilmiş bir kare, t{4}, bir sekizgendir, {8}. Dönüşümlü bir kare, h{4}, bir digondur, {2}. ⓘ

Çevre ve alan

Bir karenin alanı, kenarlarının uzunluklarının çarpımıdır. ⓘ

Dört kenarı uzun olan bir karenin çevresi $\ell$ o

P=4\ell

ⓘ

ve A alanı ise

A=\ell ^{2}.

ⓘ

Dört kare on altıya eşit olduğundan, dörde dört bir karenin alanı çevresine eşittir. Böyle bir özelliğe sahip diğer tek dörtgen üçe altı dikdörtgendir. ⓘ

Klasik zamanlarda ikinci kuvvet, yukarıdaki formülde olduğu gibi bir karenin alanı cinsinden tanımlanırdı. Bu da kare teriminin ikinci kuvvete yükseltme anlamında kullanılmasına yol açmıştır. ⓘ

Alan, d köşegeni kullanılarak aşağıdaki şekilde de hesaplanabilir

A={\frac {d^{2}}{2}}.

ⓘ

R çevre yarıçapı cinsinden, bir karenin alanı şöyledir

A=2R^{2};

ⓘ

Çünkü dairenin alanı $\pi R^{2},$ kare doluyor $2/\pi \approx 0.6366$ çevreleyen dairenin alanıdır. ⓘ

İç yarıçap r cinsinden, karenin alanı şöyledir

A=4r^{2};

ⓘ

Dolayısıyla, iç içe geçmiş dairenin alanı $\pi /4\approx 0.7854$ kareninkinden daha büyüktür. ⓘ

Düzgün bir çokgen olduğu için kare, belirli bir alanı çevreleyen en az çevreye sahip dörtgendir. Aynı şekilde kare, belirli bir çevre içinde en büyük alanı içeren dörtgendir. Gerçekten de, eğer A ve P bir dörtgen tarafından çevrelenen alan ve çevre ise, o zaman aşağıdaki izoperimetrik eşitsizlik geçerlidir:

16A\leq P^{2}

ancak ve ancak dörtgen bir kare ise eşittir. ⓘ

Köşegen uzunluğu d olmak üzere ⓘ

Diğer gerçekler

Bir karenin köşegenleri şunlardır ${\sqrt {2}}$ (yaklaşık 1,414) karenin bir kenarının uzunluğunun katıdır. Pisagor sabiti ya da 2'nin karekökü olarak bilinen bu değer, irrasyonel olduğu kanıtlanan ilk sayıdır.
Kare, açıları ikiye bölen eşit köşegenlere sahip bir paralelkenar olarak da tanımlanabilir.
Eğer bir şekil hem dikdörtgen (dik açılar) hem de eşkenar dörtgen (eşit kenar uzunlukları) ise, o zaman bir karedir.
Bir kare, aynı çevreye sahip diğer dörtgenlerden daha büyük bir alana sahiptir.
Kare döşeme, düzlemin üç düzenli döşemesinden biridir (diğerleri eşkenar üçgen ve düzgün altıgendir).
Kare, iki boyutta iki politop ailesinde yer alır: hiperküp ve çapraz politop. Kare için Schläfli sembolü {4}'tür.
Kare oldukça simetrik bir nesnedir. Dört yansıma simetrisi çizgisi vardır ve 4. dereceden dönme simetrisine sahiptir (90°, 180° ve 270° boyunca). Simetri grubu D₄ dihedral grubudur.
Bir kare herhangi bir düzgün çokgenin içine yazılabilir. Bu özelliğe sahip diğer tek çokgen eşkenar üçgendir.
Eğer bir ABCD karesinin iç içe geçmiş çemberinin AB üzerinde E, BC üzerinde F, CD üzerinde G ve DA üzerinde H teğet noktaları varsa, o zaman iç içe geçmiş çember üzerindeki herhangi bir P noktası için,

2(PH^{2}-PE^{2})=PD^{2}-PB^{2}.

Eğer $d_{i}$ düzlemdeki rastgele bir noktadan karenin i'inci köşesine olan uzaklıktır ve $R$ karenin çevre yarıçapı ise, o zaman ⓘ

{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+3R^{4}=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+R^{2}\right)^{2}.

Eğer $L$ ve $d_{i}$ düzlemdeki keyfi bir noktadan sırasıyla karenin merkez noktasına ve dört köşesine olan uzaklıklardır, o halde ⓘ

d_{1}^{2}+d_{3}^{2}=d_{2}^{2}+d_{4}^{2}=2(R^{2}+L^{2})

ve

d_{1}^{2}d_{3}^{2}+d_{2}^{2}d_{4}^{2}=2(R^{4}+L^{4}),

nerede

R

karenin çevre yarıçapıdır. ⓘ

Koordinatlar ve denklemler

|x|+|y|=2

Kartezyen koordinatlar üzerinde çizilmiştir. ⓘ

Dikey ve yatay kenarları olan, orijin merkezli ve kenar uzunluğu 2 olan bir karenin köşelerinin koordinatları (±1, ±1) iken, bu karenin içi -1 < xi < 1 ve -1 < yi < 1 olan tüm (xi, yi) noktalarından oluşur. Denklem

\max(x^{2},y^{2})=1

ⓘ

bu karenin sınırını belirtir. Bu denklem "x² veya y², hangisi büyükse, 1'e eşittir" anlamına gelir. Bu karenin çevre yarıçapı (karenin köşelerinden çizilen bir dairenin yarıçapı) karenin köşegeninin yarısıdır ve şu değere eşittir ${\sqrt {2}}.$ O zaman çemberin denklemi

x^{2}+y^{2}=2.

ⓘ

Alternatif olarak denklem ⓘ

\left|x-a\right|+\left|y-b\right|=r.

ⓘ

(a, b) merkez koordinatlarına ve r yatay veya dikey yarıçapına sahip bir karenin sınırını tanımlamak için de kullanılabilir. Bu nedenle kare, L₁ mesafe metriğine göre topolojik bir top şeklindedir. ⓘ

İnşaat

Aşağıdaki animasyonlar bir pergel ve çizgeç kullanarak bir karenin nasıl oluşturulacağını göstermektedir. Bu, ikinin kuvveti olan 4 = 2² olduğu için mümkündür. ⓘ

Belirli bir çevre çemberinde kare ⓘ

Belirli bir kenar uzunluğunda kare,
Thales teoremini kullanarak dik açı

Belirli bir köşegende kare ⓘ

Simetri

Dihedral simetriler köşelerden (diyagonal için d) veya kenarlardan (dikmeler için p) geçip geçmediklerine bağlı olarak bölünmüştür. Orta sütundaki döngüsel simetriler merkezi dönme düzenleri için g olarak etiketlenmiştir. Karenin tam simetrisi r8'dir ve simetri yok a1 olarak etiketlenmiştir. ⓘ

Kare 8. dereceden Dih₄ simetrisine sahiptir. 2 dihedral alt grubu vardır: Dih₂, Dih₁ ve 3 döngüsel alt grup: Z₄, Z₂ ve Z₁. ⓘ

Kare, birçok alt simetri dörtgeninin özel bir durumudur:

İki bitişik eşit kenarı olan bir dikdörtgen
Dört eşit kenarı ve dört dik açısı olan bir dörtgen
Bir dik açısı ve iki bitişik eşit kenarı olan bir paralelkenar
Dik açılı bir eşkenar dörtgen
Tüm açıları eşit olan bir eşkenar dörtgen
Köşegenleri eşit olan bir eşkenar dörtgen ⓘ

Bu 6 simetri bir kare üzerinde 8 farklı simetriyi ifade etmektedir. John Conway bunları bir harf ve grup sırasına göre etiketlemiştir. ⓘ

Her bir alt grup simetrisi, düzensiz dörtgenler için bir veya daha fazla serbestlik derecesine izin verir. r8 karenin tam simetrisi ve a1 simetri yok. d4 bir dikdörtgenin simetrisi ve p4 bir eşkenar dörtgenin simetrisi. Bu iki form birbirinin ikilisidir ve karenin simetri sırasının yarısına sahiptir. d2 bir ikizkenar yamuğun simetrisi ve p2 bir uçurtmanın simetrisidir. g2 bir paralelkenarın geometrisini tanımlar. ⓘ

Sadece g4 alt grubunun serbestlik derecesi yoktur, ancak yönlendirilmiş kenarları olan bir kare olarak görülebilir. ⓘ

Üçgenlerin içine yerleştirilmiş kareler

Her dar üçgenin üç adet iç karesi vardır (iç karelerin dört köşesi de üçgenin bir kenarı üzerinde yer alır, dolayısıyla karelerden ikisi aynı kenar üzerinde yer alır ve dolayısıyla karenin bir kenarı üçgenin bir kenarının bir kısmıyla çakışır). Bir dik üçgende karelerden ikisi çakışır ve üçgenin dik açısında bir tepe noktasına sahiptir, bu nedenle bir dik üçgenin yalnızca iki farklı yazılı karesi vardır. Bir geniş üçgende, bir kenarı üçgenin en uzun kenarının bir kısmıyla çakışan yalnızca bir kare vardır. ⓘ

Üçgenin alanının kare tarafından doldurulan kısmı 1/2'den fazla değildir. ⓘ

Dairenin karesini alma

Eski geometriciler tarafından önerilen çemberin karesini alma, pergel ve çizgeç ile sadece sonlu sayıda adım kullanarak verilen bir çemberle aynı alana sahip bir kare inşa etme problemidir. ⓘ

1882 yılında, pi ( $π$ )'nin cebirsel irrasyonel bir sayıdan ziyade transandantal bir sayı olduğunu, yani rasyonel katsayılı herhangi bir polinomun kökü olmadığını kanıtlayan Lindemann-Weierstrass teoreminin bir sonucu olarak bu görevin imkansız olduğu kanıtlanmıştır. ⓘ

Öklid dışı geometri

Öklidyen olmayan geometride, kareler daha genel olarak 4 eşit kenarı ve eşit açıları olan çokgenlerdir. ⓘ

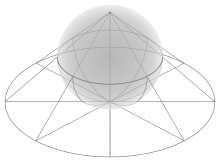
Küresel geometride kare, kenarları eşit uzaklıkta ve eşit açılarda birleşen büyük daire yayları olan bir çokgendir. Düzlem geometrisinin karesinden farklı olarak, böyle bir karenin açıları bir dik açıdan daha büyüktür. Daha büyük küresel kareler daha büyük açılara sahiptir. ⓘ

Hiperbolik geometride dik açılı kareler mevcut değildir. Bunun yerine, hiperbolik geometrideki kareler dik açılardan daha küçük açılara sahiptir. Daha büyük hiperbolik kareler daha küçük açılara sahiptir. ⓘ

Örnekler:

İki kare, her bir tepe noktası etrafında 2 kare ve 180 derecelik iç açılarla küreyi döşeyebilir. Her kare bütün bir yarımküreyi kaplar ve köşeleri büyük bir daire boyunca uzanır. Buna küresel kare dihedron denir. Schläfli sembolü {4,2}'dir.	Altı kare, her bir köşenin etrafında 3 kare ve 120 derecelik iç açılarla küreyi kaplayabilir. Buna küresel küp denir. Schläfli sembolü {4,3}'tür.	Kareler hiperbolik düzlemi her bir tepe noktası etrafında 5 kare olacak ve her bir kare 72 derecelik iç açılara sahip olacak şekilde döşeyebilir. Schläfli sembolü {4,5} şeklindedir. Aslında, herhangi bir n ≥ 5 için, her bir tepe noktası etrafında n kareli bir hiperbolik döşeme vardır. ⓘ

Çapraz kare

Çapraz kare ⓘ

Çapraz kare, bir karenin karşılıklı iki kenarının çıkarılması ve iki köşegeniyle yeniden bağlanmasıyla oluşturulan, kendi kendini kesen bir çokgen olan karenin bir yüzüdür. Karenin yarısı kadar simetriye sahiptir, Dih₂, mertebe 4. Kare ile aynı köşe düzenine sahiptir ve köşe geçişlidir. Ortak bir tepe noktasına sahip iki 45-45-90 üçgeni olarak görünür, ancak geometrik kesişme bir tepe noktası olarak kabul edilmez. ⓘ

Çapraz kare bazen papyon veya kelebeğe benzetilir. çapraz dikdörtgen, dikdörtgenin bir yüzü olarak ilişkilidir, her ikisi de çapraz dörtgenlerin özel durumlarıdır. ⓘ

Çapraz bir karenin iç kısmı, saat yönünde veya saat yönünün tersine sarım yönüne bağlı olarak her üçgende ±1'lik bir çokgen yoğunluğuna sahip olabilir. ⓘ

Bir kare ve bir çapraz kare aşağıdaki ortak özelliklere sahiptir:

Karşılıklı kenarların uzunluğu eşittir.
İki köşegenin uzunluğu eşittir.
İki yansıma simetrisi çizgisine ve 2. dereceden (180° boyunca) dönme simetrisine sahiptir. ⓘ

Düzgün bir yıldız çokyüzlü olan tetrahemihexahedronun tepe figüründe bulunur. ⓘ

Grafikler

3-simpleks (3D) ⓘ

K₄ tam grafiği genellikle 6 olası kenarın tamamının bağlı olduğu bir kare olarak çizilir, dolayısıyla her iki köşegeni de çizilmiş bir kare olarak görünür. Bu grafik aynı zamanda düzenli 3'lü simpleksin (tetrahedron) 4 köşesi ve 6 kenarının ortografik bir izdüşümünü temsil eder. ⓘ

Özellikleri

Dört kenarının da uzunluğu birbirine eşittir.
Karşılıklı kenarları birbirine paraleldir.
Dört açısı da 90 derecedir.
İç açılarının toplamı 360 derecedir.
İki adet köşegeni vardır. Bu köşegenler aynı zamanda açıortaylardır ve uzunlukları birbirlerine eşittir.
Köşegenlerin kesişme noktası 90 derecedir.
Köşegenlerin kesiştikleri nokta karenin ağırlık merkezidir.
Köşegenleri birbirini dik ortalar. ⓘ