PID
Oransal-integral-türev kontrolör (PID kontrolör veya üç terimli kontrolör), endüstriyel kontrol sistemlerinde ve sürekli modülasyonlu kontrol gerektiren çeşitli diğer uygulamalarda yaygın olarak kullanılan geri besleme kullanan bir kontrol döngüsü mekanizmasıdır. Bir PID kontrolör sürekli olarak bir hata değeri hesaplar istenen bir ayar noktası (SP) ile ölçülen bir proses değişkeni (PV) arasındaki fark olarak tanımlanır ve oransal, integral ve türev terimlerine (sırasıyla P, I ve D olarak gösterilir) dayalı bir düzeltme uygular, dolayısıyla adı da buradan gelir. ⓘ
Pratik anlamda, PID bir kontrol fonksiyonuna otomatik olarak doğru ve duyarlı bir düzeltme uygular. Günlük bir örnek, sabit motor gücü uygulandığında bir tepeye çıkmanın hızı düşüreceği bir arabadaki hız sabitleyicidir. Kontrolörün PID algoritması, motorun güç çıkışını kontrollü bir şekilde artırarak ölçülen hızı minimum gecikme ve aşma ile istenen hıza geri getirir. ⓘ
PID'nin ilk teorik analizi ve pratik uygulaması, 1920'lerin başından itibaren geliştirilen gemiler için otomatik dümen sistemleri alanındaydı. Daha sonra imalat sanayinde otomatik süreç kontrolü için kullanılmış ve önce pnömatik sonra da elektronik kontrolörlerde yaygın olarak uygulanmıştır. Günümüzde PID konsepti, doğru ve optimize edilmiş otomatik kontrol gerektiren uygulamalarda evrensel olarak kullanılmaktadır. ⓘ
Geçmişte istatistik değerleri olmayan bir sürecin ve bilginin olmadığı durumlarda, PID denetleyici algoritması tarihsel olarak en iyi denetleyici olarak kabul edilmiştir. PID kontrol algoritması üç parametre ile , özel proseslerin gereksinimleri için kontrol eylemi sağlayabilir. Denetleyicinin tepkisi hatanın denetlenerek yanıtlanması olarak tarif edilebilir. ⓘ
Temel çalışma

PID algoritması hata değerini azaltmak için üç ayrı sabit parametreyi kontrol eder, bu sebeple bazen üç aşamalı kontrol olarak adlandırılır: oransal, P ile gösterilir; integral, I ile gösterilir; türevsel, D ile gösterilir. Sezgisel olarak, bu değerler mevcut değişim göz önüne alınarak şu şekilde yorumlanabilir; P mevcut hataya bağlıdır, I geçmiş hataların toplamı ve D gelecekteki hataların bir tahminidir. Sistem, bu üç eylemin ağırlıklı toplamı yoluyla kontrol edilerek istenen duruma getirilir. Örnek olarak, bir kontrol vanasının pozisyonu ya da bir ısıtma elemanının çıkış gücü kontrol edilerek istenilen akış veya sıcaklık seviyesi en düşük hata ile elde edilmeye çalışılır. ⓘ
Yandaki blok şeması bu parametrelerin nasıl hesaplandığını ve uygulandığını göstermektedir. Şemada görüldüğü gibi PID denetleyici sürekli olarak bir hata değerini hesaplamaktadır. , amaçlanan durum ile ölçülen durum arasındaki farktır. Denetleyici oransal, integral, ve türevsel terimleri içeren bir düzeltme uygular. Bu düzeltme, bir kontrol değişkenini ayarlayarak hatayı en aza indirgemeyi amaçlar. Örneğin, düzeltme PID terimlerinin ağırlıklı toplamına göre bir kontrol valfinin döndürülmesi olabilir. ⓘ
Bu modelde:
- P terimi, SP−PV hatasının mevcut değeriyle orantılıdır. Örneğin, hata büyük ve pozitifse, kontrol çıktısı, kazanç faktörü "K" dikkate alınarak orantılı olarak büyük ve pozitif olacaktır. Orantısal kontrolün tek başına kullanılması, orantısal yanıtı oluşturmak için bir hata gerektirdiğinden, genellikle ayar noktası ile gerçek işlem değeri arasında bir hataya neden olur. Kontrolör, bir hata olmadığı sürece sistemi ayarlayamaz. ⓘ
- I terimi, SP−PV hatasının geçmiş değerlerini hesaba katar ve I terimini üretmek için bunları zaman içinde integralini alarak bütünleştirir. Örneğin, orantısal kontrol uygulamasından sonra artık bir SP−PV hatası varsa, integral terimi, hatanın geçmiş kümülatif değerine bağlı olarak bir kontrol etkisi ekleyerek artık hatayı ortadan kaldırmaya çalışır. Hata ortadan kaldırıldığında, integral terimin büyümesi duracaktır. Bu, hata azaldıkça orantılı etkinin azalmasına neden olur ancak bu, artan integral etkisi ile telafi edilir. ⓘ
- D terimi, mevcut değişim hızına dayalı olarak SP−PV hatasının gelecekteki eğiliminin en iyi tahminidir. Hata değişim oranı tarafından üretilen bir kontrol etkisi uygulayarak SP-PV hatasının etkisini etkin bir şekilde azaltmaya çalıştığı için bazen "öngörülü kontrol" (ingilizce: anticipatory control) olarak adlandırılır. Değişim ne kadar hızlı olursa, kontrol veya sönümleme etkisi o kadar büyük olur. ⓘ
Ayarlama – Optimum kontrol fonksiyonunu üretmek için bu efektlerin dengesi loop tuning ile sağlanır. Ayar sabitleri aşağıda "K" olarak gösterilmiştir ve bunlar, kontrolörün dışındaki tam döngünün yanıt özelliklerine bağlı olduklarından, her kontrol uygulaması için türetilmelidir. Bunlar, ölçüm sensörünün davranışına, son kontrol elemanına (bir kontrol valfi gibi), herhangi bir kontrol sinyali gecikmesine ve sürecin kendisine bağlıdır. Sabitlerin yaklaşık değerleri, genellikle uygulamanın türü bilinerek başlangıçta girilebilir ancak normalde bir ayar noktası değişikliği ekleyerek ve sistem yanıtını gözlemleyerek uygulamada süreci "çarparak" (ing: bumping) düzeltilir veya ayarlanır. ⓘ
Kontrol eylemi – Yukarıdaki matematiksel model ve pratik döngü, tüm terimler için bir doğrudan kontrol eylemi kullanır; bu, artan bir pozitif hatanın artan bir pozitif kontrol çıktı düzeltmesi ile sonuçlanması anlamına gelir. Olumsuz düzeltici eylem uygulanması gerekiyorsa, sisteme “ters” hareket denir. Örneğin, akış döngüsündeki valf, %0–100 kontrol çıkışı için %100–0 valf açıklığıysa bu, kontrolör eyleminin tersine çevrilmesi gerektiği anlamına gelir. Bazı proses kontrol şemaları ve nihai kontrol elemanları bu ters işlemi gerektirir. Bir örneği, soğutma suyu için kullanılan bir vana olabilir. Burada arızaya karşı emniyet (ing: fail-safe) modu, sinyal kaybında vananın %100 açılmasıdır; bu nedenle %0 kontrolör çıkışı olduğunda valfin %100 açılmasına neden olmalıdır. ⓘ
Matematiksel form
Genel kontrol fonksiyonu ⓘ
nerede , ve , hepsi negatif olmayan, sırasıyla oransal, integral ve türev terimlerinin katsayılarını gösterir (bazen P, I ve D olarak gösterilir). ⓘ
Denklemin standart formunda (makalenin ilerleyen bölümlerine bakınız), ve sırasıyla şu şekilde değiştirilir ve Bunun avantajı ise ve sırasıyla bir entegrasyon süresini ve bir türev süresini temsil ettikleri için anlaşılabilir bir fiziksel anlama sahiptirler. kontrolörün ayar noktasına yaklaşmaya çalışacağı zaman sabitidir. kontrolörün çıkışın sürekli olarak ayar noktasının üstünde veya altında olmasını ne kadar süre tolere edeceğini belirler. ⓘ
Kontrol terimlerinin seçici kullanımı
Bir PID kontrolörünün üç kontrol terimi olmasına rağmen, bazı uygulamalarda uygun kontrolü sağlamak için sadece bir veya iki terime ihtiyaç duyulur. Bu, kullanılmayan parametrelerin sıfıra ayarlanmasıyla elde edilir ve diğer kontrol eylemlerinin yokluğunda PI, PD, P veya I kontrolörü olarak adlandırılır. PI kontrolörler, türevsel eylemin ölçüm gürültüsüne duyarlı olacağı uygulamalarda oldukça yaygındır, ancak integral terimi genellikle sistemin hedef değerine ulaşması için gereklidir. ⓘ
Uygulanabilirlik
PID algoritmasının kullanılması, sistemin optimum kontrolünü veya kontrol kararlılığını garanti etmez. Aşırı gecikmelerin olduğu durumlar ortaya çıkabilir: proses değerinin ölçümü gecikir veya kontrol eylemi yeterince hızlı uygulanmaz. Bu durumlarda etkili olabilmek için lead-lag kompanzasyonu gereklidir. Kontrolörün tepkisi, bir hataya verdiği yanıt, sistemin bir ayar noktasını aşma derecesi ve herhangi bir sistem salınımının derecesi açısından tanımlanabilir. Ancak PID kontrolörü, altta yatan sürecin bilgisine veya modeline değil, yalnızca ölçülen süreç değişkeninin yanıtına dayandığı için geniş çapta uygulanabilir. ⓘ
Tarihçe


Kökenleri
Sürekli kontrol, PID kontrolörleri tam olarak anlaşılmadan ve uygulanmadan önce, bir süreci kontrol etmek için dönen ağırlıklar kullanan santrifüj regülatöründe kökenlerinden birine sahiptir. Bu, 17. yüzyılda Christiaan Huygens tarafından yel değirmenlerindeki değirmen taşları arasındaki boşluğu dönüş hızına bağlı olarak düzenlemek ve böylece tahıl beslemesinin değişken hızını telafi etmek için icat edilmiştir. ⓘ
Düşük basınçlı sabit buhar makinesinin icadıyla birlikte otomatik hız kontrolüne ihtiyaç duyuldu ve James Watt'ın kendi tasarımı olan "konik sarkaç" regülatörü, dikey bir mile bağlantı kollarıyla tutturulmuş bir dizi döner çelik bilye, bir endüstri standardı haline geldi. Bu, değirmen taşı-boşluk kontrolü konseptine dayanıyordu. ⓘ
Bununla birlikte, döner regülatör hız kontrolü, değişen yük koşulları altında hala değişkendi ve şu anda oransal kontrol olarak bilinen kontrolün tek başına yetersizliği ortadaydı. İstenen hız ile gerçek hız arasındaki hata artan yük ile birlikte artmaktaydı. 19. yüzyılda, regülatörlerin çalışmasının teorik temeli ilk olarak James Clerk Maxwell tarafından 1868 yılında şu anda ünlü olan On Governors (Regülatörler Üzerine) adlı makalesinde tanımlandı. Kontrol kararlılığının matematiksel temelini araştırdı ve bir çözüme doğru iyi bir yol kat etti, ancak matematikçilerin sorunu incelemesi için bir çağrıda bulundu. Sorun 1874'te Edward Routh, Charles Sturm ve 1895'te Adolf Hurwitz tarafından daha fazla incelenmiş ve bunların hepsi kontrol kararlılığı kriterlerinin oluşturulmasına katkıda bulunmuştur. Sonraki uygulamalarda hız regülatörleri, özellikle 1872 yılında Watt'ın konik sarkaç regülatörünü teorik olarak analiz eden Amerikalı bilim adamı Willard Gibbs tarafından daha da geliştirilmiştir. ⓘ
Bu sıralarda Whitehead torpidosunun icadı, çalışma derinliğinin doğru bir şekilde kontrol edilmesini gerektiren bir kontrol sorunu ortaya çıkardı. Tek başına bir derinlik basınç sensörünün kullanılması yetersiz kaldı ve torpidonun ön ve arka eğimini ölçen bir sarkaç, derinlik ölçümü ile birleştirilerek sarkaç ve hidrostat kontrolü haline geldi. Basınç kontrolü sadece oransal bir kontrol sağlıyordu ve eğer kontrol kazancı çok yüksekse, kararsız hale geliyor ve derinlik tutuşunda önemli bir kararsızlıkla birlikte aşıma giriyordu. Sarkaç, torpidonun dalış/tırmanış açısını ve dolayısıyla derinlik değişim hızını tespit ederek salınımları sönümleyen, günümüzde türevsel kontrol olarak bilinen kontrolü ekledi. Bu gelişme (Whitehead tarafından eylemi hakkında hiçbir ipucu vermemek için "Sır" olarak adlandırılmıştır) 1868 civarındaydı. ⓘ
PID tipi kontrolörün bir diğer erken örneği 1911 yılında Elmer Sperry tarafından gemi dümeni için geliştirilmiştir, ancak bu çalışma matematiksel temelli olmaktan ziyade sezgiseldir. ⓘ
Ancak 1922 yılına kadar, şu anda PID veya üç terimli kontrol olarak adlandırdığımız şey için resmi bir kontrol yasası ilk kez Rus-Amerikan mühendis Nicolas Minorsky tarafından teorik analiz kullanılarak geliştirilmedi. Minorsky, ABD Donanması için otomatik gemi dümenini araştırıyor ve tasarlıyordu ve analizini bir dümencinin gözlemlerine dayandırdı. Dümencinin gemiyi sadece mevcut rota hatasına göre değil, aynı zamanda geçmiş hatalara ve mevcut değişim oranına göre de yönlendirdiğini fark etti; bu daha sonra Minorsky tarafından matematiksel bir işleme tabi tutuldu. Minorsky'nin amacı genel kontrol değil istikrardı ve bu da sorunu önemli ölçüde basitleştiriyordu. Oransal kontrol küçük bozulmalara karşı kararlılık sağlarken, sabit bir bozulmayla, özellikle de integral teriminin eklenmesini gerektiren sert bir fırtınayla (sabit durum hatası nedeniyle) başa çıkmak için yetersizdi. Son olarak, kararlılığı ve kontrolü iyileştirmek için türev terimi eklenmiştir. ⓘ
USS New Mexico üzerinde, dümenin açısal hızını (açısını değil) kontrol eden kontrolörler ile denemeler gerçekleştirilmiştir. PI kontrolü ±2°'lik sürekli sapma (açısal hata) sağlamıştır. D elemanının eklenmesiyle ±1/6°'lik bir sapma hatası elde edildi ki bu çoğu dümencinin elde edebileceğinden daha iyiydi. ⓘ
Donanma nihayetinde personelin karşı çıkması nedeniyle bu sistemi benimsememiştir. Benzer çalışmalar 1930'larda birkaç kişi tarafından daha yürütülmüş ve yayınlanmıştır. ⓘ
Endüstriyel kontrol
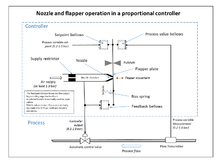
Geri besleme kontrolörlerinin yaygın kullanımı, negatif geri besleme kavramını kullanmak üzere geniş bantlı yüksek kazançlı amplifikatörlerin geliştirilmesine kadar mümkün olmamıştır. Bu, 1920'lerin sonlarında Harold Black tarafından telefon mühendisliği elektroniğinde geliştirilmiş, ancak 1934'e kadar yayınlanmamıştı. Bağımsız olarak, 1930 yılında Foxboro Company'den Clesson E Mason, 1914 yılında icat edilen nozul ve klape yüksek kazançlı pnömatik amplifikatörü, kontrolör çıkışından negatif geri besleme ile birleştirerek geniş bantlı bir pnömatik kontrolör icat etti. Bu, nozul ve klape amplifikatörünün doğrusal çalışma aralığını önemli ölçüde artırdı ve hassas bir hava alma valfi ve integral terimi üreten bir körük kullanılarak integral kontrol de eklenebildi. Sonuç, geri besleme körükleri kullanarak hem oransal hem de integral fonksiyonlar sağlayan "Stabilog" kontrolör oldu. İntegral terimi Sıfırlama olarak adlandırıldı. Daha sonra türev terimi bir başka körük ve ayarlanabilir orifis ile eklendi. ⓘ
Yaklaşık 1932'den itibaren geniş bantlı pnömatik kontrolörlerin kullanımı çeşitli kontrol uygulamalarında hızla arttı. Hava basıncı, kontrolör çıkışını üretmek ve ayrıca diyaframla çalışan kontrol valfleri gibi proses modülasyon cihazlarına güç sağlamak için kullanıldı. Bunlar, zorlu endüstriyel ortamlarda iyi çalışan ve tehlikeli yerlerde patlama riski oluşturmayan basit ve az bakım gerektiren cihazlardı. Ayrık elektronik kontrolörler ve dağıtılmış kontrol sistemleri ortaya çıkana kadar onlarca yıl boyunca endüstri standardı oldular. ⓘ
Bu kontrolörlerle birlikte, cihazların doğrusal karakteristikleri dahilinde çalışmasını sağlamak için yükseltilmiş bir sıfıra sahip olan ve %0-100 kontrol aralığını temsil eden 3-15 psi (0,2-1,0 bar) pnömatik endüstri sinyal standardı oluşturuldu. ⓘ
1950'lerde, yüksek kazançlı elektronik amplifikatörler ucuz ve güvenilir hale geldiğinde, elektronik PID kontrolörleri popüler hale geldi ve pnömatik standart 10-50 mA ve 4-20 mA akım döngüsü sinyalleri ile taklit edildi (ikincisi endüstri standardı haline geldi). Pnömatik saha aktüatörleri, proses tesisi ortamlarındaki kontrol valfleri için pnömatik enerjinin avantajları nedeniyle hala yaygın olarak kullanılmaktadır. ⓘ
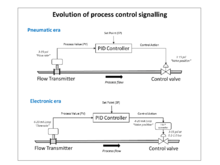
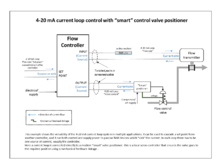
Endüstrideki modern PID kontrollerinin çoğu dağıtılmış kontrol sistemlerinde (DCS), programlanabilir mantık kontrolörlerinde (PLC'ler) veya ayrık kompakt kontrolörlerde bilgisayar yazılımı olarak uygulanmaktadır. ⓘ
Elektronik analog kontrolörler
Elektronik analog PID kontrol döngüleri genellikle daha karmaşık elektronik sistemlerde bulunurdu, örneğin bir disk sürücüsünün kafa konumlandırması, bir güç kaynağının güç koşullandırması ve hatta modern bir sismometrenin hareket algılama devresi. Ayrık elektronik analog kontrolörlerin yerini büyük ölçüde PID algoritmalarını uygulamak için mikro denetleyiciler veya FPGA'lar kullanan dijital kontrolörler almıştır. Bununla birlikte, ayrık analog PID kontrolörleri, lazer diyot kontrolörleri gibi yüksek bant genişliği ve düşük gürültü performansı gerektiren niş uygulamalarda hala kullanılmaktadır. ⓘ
Kontrol döngüsü örneği
Bir kontrol döngüsü ile hareket ettirilebilen ve konumlandırılabilen robotik bir kol düşünün. Bir elektrik motoru, uygulanan ileri veya geri güce bağlı olarak kolu kaldırabilir veya indirebilir, ancak kolun eylemsiz kütlesi, yerçekiminden kaynaklanan kuvvetler, kaldırılacak bir yük veya harici bir nesne üzerinde yapılacak iş gibi kol üzerindeki dış kuvvetler nedeniyle güç, konumun basit bir fonksiyonu olamaz.
- Algılanan konum süreç değişkenidir (PV).
- İstenen konum ayar noktası (SP) olarak adlandırılır.
- PV ve SP arasındaki fark, kolun çok düşük veya çok yüksek olup olmadığını ve ne kadar olduğunu ölçen hatadır (e).
- Sürecin girdisi (motordaki elektrik akımı) PID kontrolörünün çıktısıdır. Buna manipüle edilen değişken (MV) ya da kontrol değişkeni (CV) denir. ⓘ
Konum (PV) ölçülerek ve ayar noktasından (SP) çıkarılarak hata (e) bulunur ve kontrolör bundan motora (MV) ne kadar elektrik akımı sağlayacağını hesaplar. ⓘ
Oransal
Bariz yöntem oransal kontroldür: motor akımı mevcut hatayla orantılı olarak ayarlanır. Ancak, örneğin kolun farklı ağırlıkları kaldırması gerekiyorsa bu yöntem başarısız olur: daha büyük bir ağırlık, aşağı tarafta aynı hata için daha büyük bir kuvvet uygulanmasını gerektirir, ancak yukarı tarafta hata düşükse daha küçük bir kuvvet gerekir. İşte bu noktada integral ve türev terimleri devreye girer. ⓘ
İntegral
Bir integral terimi, sadece hataya değil, aynı zamanda hatanın devam ettiği süreye bağlı olarak eylemi artırır. Dolayısıyla, uygulanan kuvvet hatayı sıfıra getirmek için yeterli değilse, bu kuvvet zaman geçtikçe artacaktır. Saf bir "I" kontrolörü hatayı sıfıra getirebilir, ancak hem başlangıçta yavaş tepki verir (çünkü eylem başlangıçta küçük olur, anlamlı hale gelmesi zamana bağlıdır) hem de sonunda acımasız olur (hata pozitif olduğu sürece, hata sıfıra yaklaşmaya başlamış olsa bile eylem artar). ⓘ
Hata küçükken ve azalırken çok fazla integral uygulamak aşıma yol açacaktır. Aşımdan sonra, kontrolör ters yönde büyük bir düzeltme uygularsa ve istenen konumu tekrar tekrar aşarsa, çıkış ayar noktası etrafında sabit, büyüyen veya azalan bir sinüzoid şeklinde salınacaktır. Salınımların genliği zamanla artarsa, sistem kararsızdır. Eğer azalırlarsa, sistem kararlıdır. Salınımlar sabit bir büyüklükte kalırsa, sistem marjinal olarak kararlıdır. ⓘ
Türev
Bir türev terimi hatanın büyüklüğünü dikkate almaz (yani hatayı sıfıra indiremez: saf bir D kontrolörü sistemi ayar noktasına getiremez), ancak hatanın değişim oranını dikkate alır ve bu oranı sıfıra indirmeye çalışır. Hata yörüngesini yatay bir çizgide düzleştirmeyi, uygulanan kuvveti sönümlemeyi ve böylece aşımı (uygulanan kuvvetin çok büyük olması nedeniyle diğer taraftaki hata) azaltmayı amaçlar. ⓘ
Kontrol sönümlemesi
İstenen konuma (SP) zamanında ve doğru bir şekilde kontrollü bir varış elde etmek için, kontrollü sistemin kritik bir şekilde sönümlenmesi gerekir. İyi ayarlanmış bir konum kontrol sistemi aynı zamanda kontrol edilen motora gerekli akımları uygulayarak kolun gerekli konumdan uzaklaştırmaya çalışan dış kuvvetlere karşı koymak için gerektiği kadar itmesini ve çekmesini sağlar. Ayar noktasının kendisi PLC veya başka bir bilgisayar sistemi gibi harici bir sistem tarafından oluşturulabilir, böylece robotik kolun yapması beklenen işe bağlı olarak sürekli değişir. İyi ayarlanmış bir PID kontrol sistemi, kolun bu değişen gereksinimleri en iyi şekilde karşılamasını sağlayacaktır. ⓘ
Bozukluklara yanıt
Eğer bir kontrolör sıfır hata (PV = SP) ile kararlı bir durumdan başlarsa, kontrolör tarafından yapılan diğer değişiklikler, prosesi ve dolayısıyla PV'yi etkileyen prosesin diğer ölçülen veya ölçülmeyen girdilerindeki değişikliklere yanıt olacaktır. Süreci MV dışında etkileyen değişkenler bozulmalar olarak bilinir. Genel olarak, kontrolörler bozuklukları reddetmek ve ayar noktası değişikliklerini uygulamak için kullanılır. Kol üzerindeki yükte meydana gelen bir değişiklik, robot kolu kontrol süreci için bir bozulma teşkil eder. ⓘ
Uygulamalar
Teorik olarak bir kontrolör, ölçülebilir bir çıktıya (PV), bu çıktı için bilinen bir ideal değere (SP) ve ilgili PV'yi etkileyecek sürece bir girdiye (MV) sahip herhangi bir süreci kontrol etmek için kullanılabilir. Kontrolörler endüstride sıcaklık, basınç, kuvvet, besleme hızı, akış hızı, kimyasal bileşim (bileşen konsantrasyonları), ağırlık, konum, hız ve ölçümün mevcut olduğu diğer tüm değişkenleri düzenlemek için kullanılır. ⓘ
Kontrolör teorisi
- Bu bölümde PID kontrolörünün paralel veya etkileşimsiz formu açıklanmaktadır. Diğer formlar için lütfen Alternatif isimlendirme ve formlar bölümüne bakınız. ⓘ
PID kontrol şeması adını, toplamı manipüle edilen değişkeni (MV) oluşturan üç düzeltme teriminden alır. Oransal, integral ve türev terimleri, PID kontrolörün çıkışını hesaplamak için toplanır. Tanımlama kontrolör çıkışı olarak, PID algoritmasının son şekli şöyledir
nerede
- bir ayarlama parametresi olan oransal kazançtır,
- bir ayarlama parametresi olan integral kazancıdır,
- bir ayarlama parametresi olan türev kazancıdır,
- hatadır (SP ayar noktası ve PV(t) proses değişkenidir),
- zaman veya anlık zamandır (şimdiki zaman),
- entegrasyon değişkenidir (0 zamanından günümüze kadar değerler alır) ). ⓘ
Eşdeğer olarak, PID kontrolörün Laplace alanındaki transfer fonksiyonu şöyledir
nerede karmaşık frekanstır. ⓘ
Oransal terim

Oransal terim, mevcut hata değeriyle orantılı bir çıkış değeri üretir. Oransal yanıt, hatanın oransal kazanç sabiti olarak adlandırılan bir Kp sabiti ile çarpılmasıyla ayarlanabilir. ⓘ
Oransal terim şu şekilde verilir
Yüksek bir oransal kazanç, hatadaki belirli bir değişiklik için çıkışta büyük bir değişiklikle sonuçlanır. Oransal kazanç çok yüksekse sistem kararsız hale gelebilir (döngü ayarlama bölümüne bakın). Buna karşılık, küçük bir kazanç, büyük bir giriş hatasına küçük bir çıkış tepkisi ve daha az duyarlı veya daha az duyarlı bir kontrolör ile sonuçlanır. Oransal kazanç çok düşükse, sistem bozukluklarına yanıt verirken kontrol eylemi çok küçük olabilir. Ayarlama teorisi ve endüstriyel uygulama, oransal terimin çıkış değişiminin büyük kısmına katkıda bulunması gerektiğini göstermektedir. ⓘ
Kararlı durum hatası
Kararlı durum hatası, istenen nihai çıkış ile gerçek çıkış arasındaki farktır. Sürmek için sıfır olmayan bir hata gerektiğinden, oransal bir kontrolör genellikle kararlı durum hatası ile çalışır. Kararlı durum hatası (SSE) proses kazancı ile orantılı ve oransal kazanç ile ters orantılıdır. SSE, ayar noktası AND çıkışına dengeleyici bir sapma terimi eklenerek azaltılabilir veya bir integral terimi eklenerek dinamik olarak düzeltilebilir. ⓘ
İntegral terimi
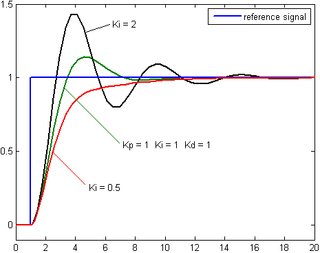
İntegral teriminin katkısı hem hatanın büyüklüğü hem de hatanın süresi ile orantılıdır. Bir PID kontrolöründeki integral, zaman içindeki anlık hatanın toplamıdır ve daha önce düzeltilmiş olması gereken birikmiş ofseti verir. Biriken hata daha sonra integral kazancı (Ki) ile çarpılır ve kontrolör çıkışına eklenir. ⓘ
İntegral terimi şu şekilde verilir
İntegral terimi, prosesin ayar noktasına doğru hareketini hızlandırır ve saf oransal kontrolörde meydana gelen artık kararlı durum hatasını ortadan kaldırır. Bununla birlikte, integral terimi geçmişten gelen birikmiş hatalara yanıt verdiğinden, mevcut değerin ayar noktası değerini aşmasına neden olabilir (döngü ayarlama bölümüne bakın). ⓘ
Türevsel terim
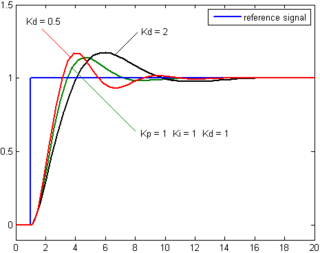
Proses hatasının türevi, hatanın zaman içindeki eğimi belirlenerek ve bu değişim oranı türev kazancı Kd ile çarpılarak hesaplanır. Türev teriminin genel kontrol eylemine katkısının büyüklüğü türev kazancı, Kd olarak adlandırılır. ⓘ
Türev terimi şu şekilde verilir
Türev eylemi sistem davranışını tahmin eder ve böylece sistemin yerleşme süresini ve kararlılığını iyileştirir. İdeal bir türev nedensel değildir, bu nedenle PID kontrolörlerinin uygulamaları, yüksek frekanslı kazancı ve gürültüyü sınırlamak için türev terimi için ek bir düşük geçişli filtreleme içerir. Türev işlemi, gerçek dünya uygulamalarında sistem kararlılığı üzerindeki değişken etkisi nedeniyle pratikte nadiren kullanılır - bir tahmine göre konuşlandırılmış kontrolörlerin yalnızca %25'inde -. ⓘ
Döngü ayarlama
Bir kontrol döngüsünün ayarlanması, kontrol parametrelerinin (oransal bant/kazanç, integral kazanç/reset, türevsel kazanç/oran) istenen kontrol yanıtı için optimum değerlere ayarlanmasıdır. Kararlılık (sınırsız salınım olmaması) temel bir gerekliliktir, ancak bunun ötesinde, farklı sistemler farklı davranışlara sahiptir, farklı uygulamaların farklı gereksinimleri vardır ve gereksinimler birbiriyle çelişebilir. ⓘ
Sadece üç parametre olmasına ve prensipte tanımlanması basit olmasına rağmen, PID ayarlaması zor bir problemdir çünkü PID kontrolünün sınırlamaları dahilinde karmaşık kriterleri karşılaması gerekir. Buna göre, döngü ayarı için çeşitli yöntemler vardır ve daha sofistike teknikler patentlere konu olmuştur; bu bölümde döngü ayarı için bazı geleneksel, manuel yöntemler açıklanmaktadır. ⓘ
Bir PID kontrolörünün tasarlanması ve ayarlanması kavramsal olarak sezgisel gibi görünse de, kısa geçici ve yüksek kararlılık gibi birden fazla (ve genellikle birbiriyle çelişen) hedefe ulaşılmak isteniyorsa pratikte zor olabilir. PID kontrolörleri genellikle varsayılan ayarlar kullanılarak kabul edilebilir kontrol sağlar, ancak performans genellikle dikkatli ayarlama ile iyileştirilebilir ve kötü ayarlama ile performans kabul edilemez olabilir. Genellikle ilk tasarımların, kapalı döngü sistemi istenildiği gibi performans gösterene veya ödün verene kadar bilgisayar simülasyonları aracılığıyla tekrar tekrar ayarlanması gerekir. ⓘ
Bazı proseslerde doğrusal olmama derecesi vardır, bu nedenle tam yük koşullarında iyi çalışan parametreler proses yüksüz olarak başlatıldığında çalışmaz. Bu durum kazanç planlamasıyla (farklı çalışma bölgelerinde farklı parametreler kullanarak) düzeltilebilir. ⓘ
Kararlılık
PID kontrolör parametreleri (oransal, integral ve türev terimlerinin kazançları) yanlış seçilirse, kontrol edilen proses girişi kararsız olabilir; yani, çıkışı salınımlı veya salınımsız olarak sapar ve yalnızca doygunluk veya mekanik kırılma ile sınırlıdır. Kararsızlık, özellikle önemli bir gecikmenin varlığında aşırı kazançtan kaynaklanır. ⓘ
Genel olarak, tepkinin stabilizasyonu gereklidir ve proses, proses koşulları ve ayar noktalarının herhangi bir kombinasyonu için salınım yapmamalıdır, ancak bazen marjinal stabilite (sınırlı salınım) kabul edilebilir veya istenebilir. ⓘ
Matematiksel olarak, kararsızlığın kökenleri Laplace alanında görülebilir. ⓘ
Toplam döngü transfer fonksiyonu şöyledir:
nerede PID transfer fonksiyonudur ve tesis transfer fonksiyonudur. Kapalı döngü transfer fonksiyonunun bazı durumlarda sapma gösterdiği bir sistem kararsızdır . Bu, aşağıdaki durumlarda gerçekleşir . Tipik olarak bu durum şu durumlarda gerçekleşir 180 derecelik bir faz kayması ile. Kararlılık şu durumlarda garanti edilir yüksek faz kaymalarına maruz kalan frekanslar için. Bu etkinin daha genel bir formalizmi Nyquist kararlılık kriteri olarak bilinir. ⓘ
Optimal davranış
Bir proses değişikliğinde veya ayar noktası değişikliğinde optimum davranış uygulamaya bağlı olarak değişir. ⓘ
İki temel gereksinim regülasyon (bozulma reddi - belirli bir ayar noktasında kalma) ve komut takibidir (ayar noktası değişikliklerini uygulama). Bu terimler, kontrol edilen değişkenin istenen değeri ne kadar iyi izlediğini ifade eder. Komut takibi için spesifik kriterler yükselme süresi ve yerleşme süresini içerir. Bazı prosesler, örneğin güvenli olmayacaksa, proses değişkeninin ayar noktasının ötesine geçmesine izin vermemelidir. Diğer prosesler yeni bir ayar noktasına ulaşırken harcanan enerjiyi en aza indirmelidir. ⓘ
Ayarlama yöntemlerine genel bakış
Bir PID döngüsünü ayarlamak için çeşitli yöntemler vardır. En etkili yöntemler genellikle bir tür proses modeli geliştirmeyi ve ardından dinamik model parametrelerine dayalı olarak P, I ve D'yi seçmeyi içerir. Manuel ayarlama yöntemleri, özellikle uzun döngü sürelerine sahip sistemler için nispeten zaman alıcı olabilir. ⓘ
Yöntem seçimi büyük ölçüde döngünün ayarlama için çevrimdışına alınıp alınamayacağına ve sistemin tepki süresine bağlıdır. Sistem çevrimdışı alınabiliyorsa, en iyi ayarlama yöntemi genellikle sistemi girişte bir adım değişikliğine tabi tutmayı, çıkışı zamanın bir fonksiyonu olarak ölçmeyi ve kontrol parametrelerini belirlemek için bu yanıtı kullanmayı içerir. ⓘ
| Yöntem | Avantajlar | Dezavantajlar ⓘ |
|---|---|---|
| Manuel ayarlama | Matematik gerektirmez; çevrimiçi. | Deneyimli personel gerektirir. |
| Ziegler-Nichols | Kanıtlanmış yöntem; çevrimiçi. | Süreç karışık, biraz deneme-yanılma, çok agresif ayarlama. |
| Tyreus Luyben | Kanıtlanmış yöntem; çevrimiçi. | Süreç karışık, biraz deneme-yanılma, çok agresif ayarlama. |
| Yazılım araçları | Tutarlı ayarlama; çevrimiçi veya çevrimdışı - bilgisayar otomatik kontrol sistemi tasarımı (CAutoD) tekniklerini kullanabilir; valf ve sensör analizini içerebilir; indirmeden önce simülasyona izin verir; sabit olmayan durum (NSS) ayarlamasını destekleyebilir. | Bir miktar maliyet veya eğitim söz konusudur. |
| Cohen-Coon | İyi süreç modelleri. | Biraz matematik; çevrimdışı; sadece birinci dereceden süreçler için iyi. |
| Åström-Hägglund | Otomatik ayarlama için kullanılabilir; genlik minimumdur, bu nedenle bu yöntem en düşük işlem üzüntüsüne sahiptir | Sürecin kendisi doğası gereği salınımlıdır. |
Manuel ayarlama
Sistemin çevrimiçi kalması gerekiyorsa, bir ayarlama yöntemi ilk olarak ve değerlerini sıfıra getirin. Artırmak döngü çıkışı salınım yapana kadar; daha sonra "çeyrek genlikli bozunma" tipi bir yanıt için bu değerin yaklaşık yarısına kadar. Sonra artırın herhangi bir ofset işlem için yeterli sürede düzeltilene kadar, ancak çok büyük bir değer kararsızlığa neden olana kadar değil. Son olarak, artırın Gerekirse, döngü bir yük bozukluğundan sonra referansına kabul edilebilir bir şekilde hızlı ulaşana kadar. Çok fazla aşırı tepki ve aşıma neden olur. Hızlı bir PID döngü ayarı genellikle ayar noktasına daha hızlı ulaşmak için biraz aşım yapar; ancak bazı sistemler aşımı kabul edemez, bu durumda aşırı sönümlü bir kapalı döngü sistemi gereklidir ve bu da bir yarısından önemli ölçüde daha az ayarlanması salınıma neden olan ayar. ⓘ
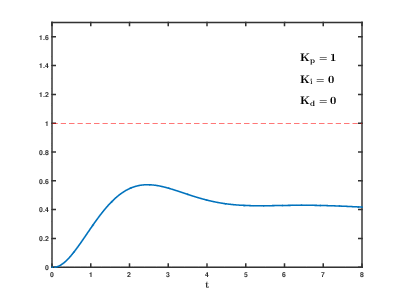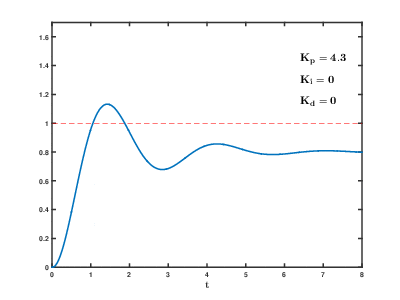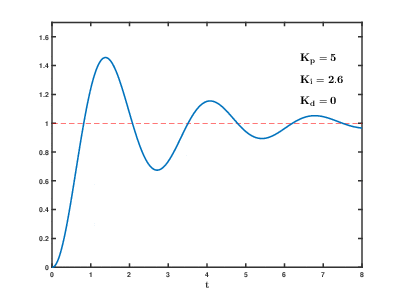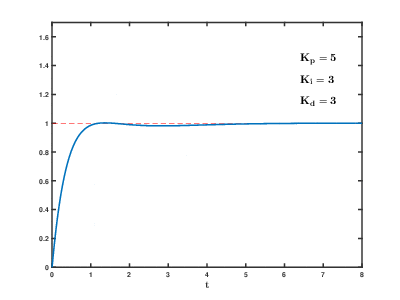
| Parametre | Yükselme süresi | Aşım | Yerleşme süresi | Kararlı durum hatası | Kararlılık ⓘ |
|---|---|---|---|---|---|
| Azalma | Artış | Küçük değişiklikler | Azalma | Degrade | |
| Azalma | Artış | Artış | Ortadan kaldırmak | Degrade | |
| Küçük değişiklik | Azalma | Azalma | Teoride bir etkisi yok | Eğer geliştirin küçük |
Ziegler-Nichols yöntemi
Bir diğer sezgisel ayarlama yöntemi, 1940'larda John G. Ziegler ve Nathaniel B. Nichols tarafından tanıtılan Ziegler-Nichols yöntemi olarak bilinir. Yukarıdaki yöntemde olduğu gibi ve kazançlar ilk olarak sıfıra ayarlanır. Oransal kazanç nihai kazanca ulaşana kadar artırılır, 'de döngünün çıkışı sürekli salınmaya başlar. ve salınım periyodu kazançları aşağıdaki gibi ayarlamak için kullanılır:
| Kontrol Tipi | |||
|---|---|---|---|
| P | — | — | |
| PI | — | ||
| PID |
Bu kazançlar PID kontrolörünün ideal, paralel formu için geçerlidir. Standart PID formuna uygulandığında, sadece integral ve türev kazançları ve salınım periyoduna bağlıdır . ⓘ
Cohen-Coon parametreleri
Bu yöntem 1953 yılında geliştirilmiştir ve birinci dereceden + zaman gecikmesi modeline dayanmaktadır. Ziegler-Nichols yöntemine benzer şekilde, aşağıdaki bozunma oranına sahip bir kapalı döngü yanıtı elde etmek için bir dizi ayarlama parametresi geliştirilmiştir . Bu parametrelerle ilgili tartışmasız en büyük sorun, süreç parametrelerindeki küçük bir değişikliğin kapalı döngü bir sistemin kararsız hale gelmesine neden olabilmesidir. ⓘ
Röle (Åström-Hägglund) yöntemi
1984 yılında Karl Johan Åström ve Tore Hägglund tarafından yayınlanan röle yöntemi, süreci geçici olarak bang-bang kontrolü kullanarak çalıştırır ve ortaya çıkan salınımları ölçer. Çıkış, kontrol değişkeninin iki değeri arasında değiştirilir (sanki bir röleyle, dolayısıyla adı). Değerler, prosesin ayar noktasını geçeceği şekilde seçilmelidir, ancak %0 ve %100 olmaları gerekmez; uygun değerler seçilerek tehlikeli salınımlardan kaçınılabilir. ⓘ
Proses değişkeni ayar noktasının altında olduğu sürece, kontrol çıkışı daha yüksek değere ayarlanır. Ayar noktasının üzerine çıkar çıkmaz, kontrol çıkışı daha düşük değere ayarlanır. İdeal olarak, çıkış dalga formu neredeyse kare şeklindedir ve ayar noktasının üstünde ve altında eşit zaman harcar. Ortaya çıkan salınımların periyodu ve genliği ölçülür ve nihai kazanç ve periyodu hesaplamak için kullanılır, bunlar daha sonra Ziegler-Nichols yöntemine beslenir. ⓘ
Spesifik olarak, nihai dönem gözlemlenen süreye eşit olduğu varsayılır ve nihai kazanç şu şekilde hesaplanır Burada a proses değişkeni salınımının genliği, b ise buna neden olan kontrol çıkışı değişiminin genliğidir. ⓘ
Röle yönteminin çok sayıda çeşidi vardır. ⓘ
Ölü zaman modeli ile birinci derece
Ölü zamana sahip birinci dereceden bir süreç için transfer fonksiyonu şöyledir: ⓘ
Burada kp proses kazancı, τp zaman sabiti, θ ölü zaman ve u(s) bir adım değişim girdisidir. Bu transfer fonksiyonunu zaman alanına dönüştürmek: ⓘ
yukarıda bulunan aynı parametreleri kullanarak. ⓘ
Bu yöntemi kullanırken, çıktının ölçülebilmesi için yeterince büyük bir adım değişikliği girişi uygulamak önemlidir; ancak, çok büyük bir adım değişikliği sürecin kararlılığını etkileyebilir. Ek olarak, daha büyük bir adım değişikliği çıkışın bir bozulma nedeniyle değişmemesini sağlar (en iyi sonuçlar için, adım testini gerçekleştirirken bozulmaları en aza indirmeye çalışın). ⓘ
Birinci dereceden proses için parametreleri belirlemenin bir yolu da %63,2 yöntemini kullanmaktır. Bu yöntemde proses kazancı (kp), çıkıştaki değişimin girişteki değişime bölünmesine eşittir. Ölü zaman (θ), adım değişiminin gerçekleştiği zaman ile çıktının ilk değiştiği zaman arasındaki süredir. Zaman sabiti (τp), adım değişikliğinden sonra çıkışın yeni kararlı durum değerinin %63,2'sine ulaşması için geçen süredir. Bu yöntemi kullanmanın bir dezavantajı, süreç büyük zaman sabitlerine sahipse yeni bir kararlı durum değerine ulaşmanın biraz zaman alabilmesidir. ⓘ
Ayarlama yazılımı
Modern endüstriyel tesislerin çoğu artık yukarıda gösterilen manuel hesaplama yöntemlerini kullanarak döngüleri ayarlamamaktadır. Bunun yerine, tutarlı sonuçlar elde etmek için PID ayarlama ve döngü optimizasyon yazılımı kullanılmaktadır. Bu yazılım paketleri veri toplar, proses modelleri geliştirir ve optimum ayarlama önerir. Hatta bazı yazılım paketleri referans değişikliklerden veri toplayarak ayarlama geliştirebilir. ⓘ
Matematiksel PID döngü ayarı sistemde bir dürtü oluşturur ve ardından PID döngü değerlerini tasarlamak için kontrol edilen sistemin frekans tepkisini kullanır. Birkaç dakikalık tepki sürelerine sahip döngülerde matematiksel döngü ayarı önerilir, çünkü deneme yanılma yöntemiyle kararlı bir döngü değerleri kümesi bulmak günler alabilir. Optimal değerleri bulmak daha zordur. Bazı dijital döngü kontrolörleri, çok küçük ayar noktası değişikliklerinin prosese gönderildiği ve kontrolörün kendisinin optimum ayar değerlerini hesaplamasına olanak tanıyan bir kendi kendine ayarlama özelliği sunar. ⓘ
Başka bir yaklaşım, Ziegler-Nichols yöntemi ile başlangıç değerlerini hesaplar ve daha iyi PID katsayıları bulmak için sayısal bir optimizasyon tekniği kullanır. ⓘ
Döngüyü farklı performans kriterlerine göre ayarlamak için başka formüller de mevcuttur. Birçok patentli formül artık PID ayarlama yazılımı ve donanım modülleri içine yerleştirilmiştir. ⓘ
Otomatik PID döngü ayarlama yazılımındaki gelişmeler, dinamik veya durağan olmayan durum (NSS) senaryosunda PID Döngülerini ayarlamak için algoritmalar da sunmaktadır. Yazılım, bir sürecin dinamiklerini bir bozulma yoluyla modeller ve yanıt olarak PID kontrol parametrelerini hesaplar. ⓘ
Sınırlamalar
PID kontrolörleri birçok kontrol problemine uygulanabilir ve genellikle herhangi bir iyileştirme olmadan veya sadece kaba ayarlama ile tatmin edici bir performans gösterirken, bazı uygulamalarda kötü performans gösterebilir ve genel olarak optimum kontrol sağlamaz. PID kontrolünün temel zorluğu, sabit parametreleri olan ve süreç hakkında doğrudan bilgi sahibi olmayan bir geri besleme kontrol sistemi olması ve bu nedenle genel performansın reaktif ve bir uzlaşma olmasıdır. PID kontrolü, sürecin modeli olmayan bir gözlemcide en iyi kontrolör olsa da, bir gözlemciye başvurmadan sürecin aktörünü açıkça modelleyerek daha iyi performans elde edilebilir. ⓘ
PID kontrolörleri, tek başlarına kullanıldıklarında, kontrol sisteminin kontrol ayar noktası değerini aşmaması, salınım yapmaması veya bu değer etrafında dolaşmaması için PID döngü kazançlarının azaltılması gerektiğinde düşük performans verebilirler. Ayrıca doğrusal olmayan durumların varlığında zorluklar yaşarlar, düzenleme ile tepki süresi arasında denge kurabilirler, değişen süreç davranışına tepki vermezler (örneğin, süreç ısındıktan sonra değişir) ve büyük bozulmalara yanıt vermede gecikme yaşarlar. ⓘ
En önemli iyileştirme, sistem hakkında bilgi sahibi olarak ileri beslemeli kontrolü dahil etmek ve PID'yi yalnızca hatayı kontrol etmek için kullanmaktır. Alternatif olarak, PID'ler parametrelerin değiştirilmesi (farklı kullanım durumlarında kazanç planlaması veya performansa göre uyarlamalı olarak değiştirilmesi), ölçümün iyileştirilmesi (daha yüksek örnekleme oranı, hassasiyet ve doğruluk ve gerekirse düşük geçişli filtreleme) veya birden fazla PID kontrolörünün basamaklandırılması gibi daha küçük yollarla değiştirilebilir. ⓘ
Doğrusallık ve simetri
PID kontrolörleri, kontrol edilecek döngü doğrusal ve simetrik olduğunda en iyi şekilde çalışır. Bu nedenle, doğrusal olmayan ve asimetrik sistemlerdeki performansları düşer. ⓘ
Örneğin bir akış kontrol uygulamasında doğrusal olmayan bir valf, değişken döngü hassasiyetine neden olur ve kararsızlığı önlemek için sönümleme eylemi gerektirir. Bir çözüm, bunu telafi etmek için kontrol algoritmasında vananın doğrusal olmayan karakteristiğinin kullanılmasıdır. ⓘ
Örneğin asimetrik bir uygulama, yalnızca pasif soğutmanın mevcut olduğu, yalnızca aktif ısıtma (bir ısıtma elemanı aracılığıyla) kullanan HVAC sistemlerinde sıcaklık kontrolüdür. Kontrol edilen sıcaklığın düşürülmesi istendiğinde ısıtma çıkışı kapatılır, ancak kontrol çıkışı nedeniyle aktif soğutma yoktur. Bu nedenle yükselen sıcaklıktaki herhangi bir aşım sadece yavaşça düzeltilebilir; kontrol çıkışı tarafından aşağıya doğru zorlanamaz. Bu durumda PID kontrolörü, aşımı önlemek veya azaltmak için aşırı sönümlenecek şekilde ayarlanabilir, ancak bu, yükselen sıcaklığın ayar noktasına yerleşme süresini artırarak performansı düşürür. Bu uygulamada kontrol kalitesinin doğal olarak bozulması aktif soğutma uygulaması ile çözülebilir. ⓘ
Türev teriminde gürültü
Türev terimiyle ilgili bir sorun, çıkışta büyük miktarda değişikliğe neden olabilecek daha yüksek frekanslı ölçüm veya işlem gürültüsünü yükseltmesidir. Yüksek frekanslı gürültü bileşenlerini ortadan kaldırmak için ölçümleri düşük geçişli bir filtre ile filtrelemek genellikle yararlıdır. Alçak geçiren filtreleme ve türev kontrolü birbirini iptal edebileceğinden, filtreleme miktarı sınırlıdır. Bu nedenle, düşük gürültülü enstrümantasyon önemli olabilir. Filtreleme verimliliğini ve pratik performansı artıran doğrusal olmayan bir medyan filtre kullanılabilir. Bazı durumlarda, diferansiyel bant çok az kontrol kaybıyla kapatılabilir. Bu, PID kontrolörünü PI kontrolörü olarak kullanmaya eşdeğerdir. ⓘ
Algoritmada yapılan değişiklikler
Temel PID algoritması, kontrol uygulamalarında PID formunda yapılan küçük değişikliklerle ele alınan bazı zorluklar sunar. ⓘ
İntegral sarma
İdeal PID uygulamalarından kaynaklanan yaygın bir sorun integral sarmasıdır. Ayar noktasındaki büyük bir değişikliğin ardından integral terimi, düzenleme değişkeni için maksimum değerden daha büyük bir hata biriktirebilir (sarma), böylece sistem aşırı aşım yapar ve bu biriken hata çözülene kadar artmaya devam eder. Bu sorun şu şekilde ele alınabilir:
- PV kontrol edilebilir bölgeye girene kadar entegrasyonun devre dışı bırakılması
- İntegral teriminin önceden belirlenmiş sınırların üzerinde veya altında birikmesini önleme
- Regülatör çıkışını uygulanabilir sınırlar içinde kısıtlamak için integral teriminin geri hesaplanması. ⓘ
Bilinen bozukluklardan kaynaklanan aşım
Örneğin, sistemin stabilize olduğu bir elektrikli rezistans fırınının sıcaklığını kontrol etmek için bir PID döngüsü kullanılır. Şimdi kapı açıldığında ve fırına soğuk bir şey konulduğunda sıcaklık ayar noktasının altına düşer. Kontrolörün integral fonksiyonu, pozitif yönde başka bir hata ekleyerek hatayı telafi etme eğilimindedir. Bu aşım, kontrol döngüsünün tipik olarak fırını yeniden ısıtmak için ihtiyaç duyduğu süre boyunca kapının açılmasından sonra integral fonksiyonunun dondurulmasıyla önlenebilir. ⓘ
PI kontrolörü

PI kontrolör (oransal-integral kontrolör), hatanın türevinin (D) kullanılmadığı PID kontrolörün özel bir durumudur. ⓘ
Kontrolör çıkışı şu şekilde verilir
nerede gerçek ölçülen değerin (PV) ayar noktasından (SP) hatası veya sapmasıdır.
Bir PI kontrolörü, Laplace operatörlerini içeren bir "akış şeması" kutusu kullanılarak Simulink veya Xcos gibi yazılımlarda kolayca modellenebilir:
nerede
- = oransal kazanç
- = integral kazanç ⓘ
İçin bir değer ayarlama genellikle aşımı azaltma ve yerleşme süresini artırma arasında bir denge vardır. ⓘ
Türev eylemin olmaması, gürültülü veri durumunda sistemi kararlı durumda daha istikrarlı hale getirebilir. Bunun nedeni, türev işleminin girdilerdeki daha yüksek frekanslı terimlere daha duyarlı olmasıdır. ⓘ
Türev eylem olmadan, PI kontrollü bir sistem durumdaki gerçek (gürültüsüz) ve nispeten hızlı değişikliklere daha az duyarlıdır ve bu nedenle sistemin ayar noktasına ulaşması daha yavaş olacak ve iyi ayarlanmış bir PID sistemine göre pertürbasyonlara yanıt vermesi daha yavaş olacaktır. ⓘ
Ölü bant
Birçok PID döngüsü mekanik bir cihazı (örneğin bir valf) kontrol eder. Mekanik bakım önemli bir maliyet olabilir ve aşınma, bir giriş sinyaline verilen mekanik tepkide ya stiction ya da backlash şeklinde kontrolün bozulmasına yol açar. Mekanik aşınma oranı esas olarak bir cihazın değişiklik yapmak için ne sıklıkta etkinleştirildiğinin bir fonksiyonudur. Aşınmanın önemli bir sorun olduğu durumlarda, PID döngüsü, çıkışın (valf) aktivasyon sıklığını azaltmak için bir çıkış ölü bandına sahip olabilir. Bu, değişiklik küçük olacaksa (tanımlanan ölü bant aralığında) kontrolörün çıkışını sabit tutacak şekilde değiştirilmesiyle gerçekleştirilir. Gerçek çıkış değişmeden önce hesaplanan çıkışın ölü banttan çıkması gerekir. ⓘ
Ayar noktası adım değişikliği
Oransal ve türevsel terimler, bir sistem büyük bir ayar noktası değişikliği gibi hatada anlık bir adım artışına maruz kaldığında çıkışta aşırı hareket üretebilir. Türev terimi söz konusu olduğunda bu durum, anlık bir adım değişikliği durumunda çok büyük olan hatanın türevinin alınmasından kaynaklanır. Sonuç olarak, bazı PID algoritmaları aşağıdaki modifikasyonlardan bazılarını içerir:
- Ayar noktası rampası
- Bu modifikasyonda, ayar noktası doğrusal veya birinci dereceden diferansiyel rampa fonksiyonu kullanılarak eski değerinden yeni belirlenen bir değere kademeli olarak taşınır. Bu, basit bir adım değişikliğinde mevcut olan süreksizliği önler.
- Proses değişkeninin türevi
- Bu durumda PID kontrolörü hatanın türevi yerine ölçülen proses değişkeninin (PV) türevini ölçer. Bu miktar her zaman süreklidir (yani, ayar noktasının değişmesi sonucunda asla bir adım değişikliği olmaz). Bu değişiklik, ayar noktası ağırlıklandırmanın basit bir örneğidir.
- Ayar noktası ağırlıklandırma
- Ayar noktası ağırlığı, kontrolörün oransal ve türevsel elemanlarındaki hatada ayar noktasına ayarlanabilir faktörler (genellikle 0 ile 1 arasında) ekler. İntegral terimindeki hata, kararlı durum kontrol hatalarını önlemek için gerçek kontrol hatası olmalıdır. Bu iki ekstra parametre yük bozukluklarına ve ölçüm gürültüsüne verilen yanıtı etkilemez ve kontrolörün ayar noktası yanıtını iyileştirmek için ayarlanabilir. ⓘ
İleri Besleme
Kontrol sistemi performansı, bir PID kontrolörünün geri besleme (veya kapalı döngü) kontrolü ile ileri besleme (veya açık döngü) kontrolü birleştirilerek geliştirilebilir. Sistem hakkındaki bilgi (istenen ivme ve atalet gibi) ileri beslenebilir ve genel sistem performansını iyileştirmek için PID çıktısıyla birleştirilebilir. İleri besleme değeri tek başına genellikle kontrolör çıkışının büyük bir kısmını sağlayabilir. PID kontrolörü öncelikle ayar noktası (SP) ile açık döngü kontrolüne verilen sistem yanıtı arasında kalan fark veya hatayı telafi etmek zorundadır. İleri besleme çıkışı proses geri beslemesinden etkilenmediğinden, kontrol sisteminin salınım yapmasına asla neden olmaz, böylece kararlılığı etkilemeden sistem yanıtını iyileştirir. İleri besleme, ayar noktasına ve ekstra ölçülen bozukluklara dayalı olabilir. Ayar noktası ağırlıklandırma, ileri beslemenin basit bir şeklidir. ⓘ
Örneğin, çoğu hareket kontrol sisteminde, kontrol altındaki mekanik bir yükü hızlandırmak için aktüatörden daha fazla kuvvet gerekir. Yükün hızını kontrol etmek ve aktüatör tarafından uygulanan kuvvete komut vermek için bir hız döngüsü PID kontrolörü kullanılıyorsa, istenen anlık ivmeyi almak, bu değeri uygun şekilde ölçeklendirmek ve PID hız döngüsü kontrolörünün çıkışına eklemek faydalıdır. Bu, yük her hızlandığında veya yavaşladığında, geri besleme değerinden bağımsız olarak aktüatörden orantılı miktarda kuvvet komutu verildiği anlamına gelir. Bu durumda PID döngüsü, proses ayar noktası ile geri besleme değeri arasında kalan farkı azaltmak amacıyla birleşik çıkışı değiştirmek için geri besleme bilgisini kullanır. Birleştirilmiş açık döngü ileri beslemeli kontrolör ve kapalı döngü PID kontrolör birlikte çalışarak daha duyarlı bir kontrol sistemi sağlayabilir. ⓘ
Boşta çalışma
PID kontrolörleri genellikle parametre değişiklikleri boyunca tutarlı bir proses çıktısını korumak için integral akümülatör terimini yeniden hesaplayan bir "bumpless" başlatma özelliği ile uygulanır. Kısmi bir uygulama, hatayı depolamak ve integral kazancı ile sonradan çarpmak yerine integral kazancını hata ile çarparak depolamaktır, bu da I kazancı değiştirildiğinde süreksiz çıktıyı önler, ancak P veya D kazançlarını önlemez. ⓘ
Diğer iyileştirmeler
İleri beslemeye ek olarak, PID kontrolörleri genellikle PID kazanç zamanlaması (farklı çalışma koşullarında parametrelerin değiştirilmesi), bulanık mantık veya hesaplamalı fiil mantığı gibi yöntemlerle geliştirilir. Diğer pratik uygulama sorunları kontrolöre bağlı enstrümantasyondan kaynaklanabilir. Yeterli kontrol performansı elde etmek için yeterince yüksek bir örnekleme oranı, ölçüm hassasiyeti ve ölçüm doğruluğu gereklidir. PID kontrolörünün iyileştirilmesi için bir başka yeni yöntem de kesirli mertebe kullanarak serbestlik derecesini artırmaktır. İntegratör ve diferansiyatörün sırası kontrolöre daha fazla esneklik katar. ⓘ
Kademeli kontrol
PID kontrolörlerinin belirgin bir avantajı, daha iyi dinamik performans elde etmek için iki PID kontrolörünün birlikte kullanılabilmesidir. Buna kademeli PID kontrolü denir. İki kontrolör, biri diğerinin ayar noktasını düzenleyecek şekilde düzenlendiğinde kademelidir. Bir PID kontrolörü, akışkan seviyesi veya hızı gibi birincil fiziksel parametreyi kontrol eden dış döngü kontrolörü olarak görev yapar. Diğer kontrolör, dış döngü kontrolörünün çıkışını ayar noktası olarak okuyan ve genellikle daha hızlı değişen bir parametreyi, akış hızını veya ivmeyi kontrol eden iç döngü kontrolörü olarak görev yapar. Basamaklı PID kontrolörleri kullanılarak kontrolörün çalışma frekansının artırıldığı ve nesnenin zaman sabitinin azaltıldığı matematiksel olarak kanıtlanabilir. ⓘ
Örneğin, sıcaklık kontrollü bir sirkülasyon banyosunda, her biri kendi termokupl sıcaklık sensörüne sahip iki PID kontrolörü vardır. Dış kontrolör, ısıtıcıdan uzakta bulunan ve suyun büyük kısmının sıcaklığını doğru bir şekilde okuyan bir termokupl kullanarak suyun sıcaklığını kontrol eder. Bu PID kontrolörün hata terimi, istenen banyo sıcaklığı ile ölçülen sıcaklık arasındaki farktır. Isıtıcıyı doğrudan kontrol etmek yerine, dış PID kontrolörü iç PID kontrolörü için bir ısıtıcı sıcaklığı hedefi belirler. İç PID kontrolör, ısıtıcıya bağlı bir termokupl kullanarak ısıtıcının sıcaklığını kontrol eder. İç kontrolörün hata terimi, bu ısıtıcı sıcaklığı ayar noktası ile ısıtıcının ölçülen sıcaklığı arasındaki farktır. Çıkışı, gerçek ısıtıcıyı bu ayar noktasına yakın kalacak şekilde kontrol eder. ⓘ
İki kontrolörün oransal, integral ve diferansiyel terimleri çok farklı olacaktır. Dış PID kontrolörünün uzun bir zaman sabiti vardır - tanktaki tüm suyun ısınması veya soğuması gerekir. İç döngü çok daha hızlı yanıt verir. Her kontrolör, kontrol ettiği sistemin fiziğine (tüm tankın veya sadece ısıtıcının ısı transferi ve termal kütlesi) uyacak şekilde ayarlanabilir ve daha iyi toplam yanıt verir. ⓘ
Alternatif isimlendirme ve formlar
Standart ve paralel (ideal) form
Endüstride en sık karşılaşılan ve ayarlama algoritmalarıyla en ilgili olan PID kontrolör formu standart formdur. Bu formda kazancına uygulanır. ve terimlerini verir:
nerede
- integral zamanıdır
- türev alma zamanıdır ⓘ
Bu standart formda, parametrelerin açık bir fiziksel anlamı vardır. Özellikle iç toplama, gelecek ve geçmiş hatalar için telafi edilen yeni bir tek hata değeri üretir. Oransal hata terimi mevcut hatadır. Türev bileşenleri terimi, aşağıdaki durumlarda hata değerini tahmin etmeye çalışır Döngü kontrolünün değişmediği varsayılarak gelecekteki saniyeler (veya örnekler). İntegral bileşeni, geçmişteki tüm hataların toplamını telafi etmek için hata değerini ayarlar ve bunları gelecekte tamamen ortadan kaldırmayı amaçlar. saniye (veya örnek). Elde edilen telafi edilmiş tek hata değeri daha sonra tek kazanç ile ölçeklendirilir kontrol değişkenini hesaplamak için. ⓘ
Kontrolör teorisi bölümünde gösterilen paralel formda
kazanç parametreleri standart formun parametreleri ile şu şekilde ilişkilidir ve . Parametrelerin basit kazançlar olarak ele alındığı bu paralel form en genel ve esnek formdur. Bununla birlikte, parametrelerin fiziksel davranışlarla en zayıf ilişkiye sahip olduğu formdur ve genellikle PID kontrolörünün teorik olarak ele alınması için ayrılmıştır. Standart form, matematiksel olarak biraz daha karmaşık olmasına rağmen endüstride daha yaygındır. ⓘ
Karşılıklı kazanç, diğer adıyla oransal bant
Birçok durumda, PID kontrolörü tarafından manipüle edilen değişken çıktısı, mümkün olan maksimum değerin %0 ila %100'ü arasında boyutsuz bir kesirdir ve gerçek birimlere (pompalama hızı veya ısıtıcı gücü watt'ı gibi) çevrilmesi PID kontrolörünün dışındadır. Ancak proses değişkeni sıcaklık gibi boyutlandırılmış birimlerdedir. Bu durumda kazancı ifade etmek yaygındır "derece başına çıktı" olarak değil, daha ziyade orantılı bir bandın karşılıklı formunda "tam çıkış başına derece": çıkışın 0 ila 1 (%0 ila %100) arasında değiştiği aralık. Bu aralığın ötesinde, çıkış doymuş, tam kapalı veya tam açıktır. Bu bant ne kadar dar olursa, oransal kazanç o kadar yüksek olur. ⓘ
Türevsel eylemin PV'ye dayandırılması
Çoğu ticari kontrol sisteminde, türevsel eylem hatadan ziyade proses değişkenine dayanır. Yani, ayar noktasındaki bir değişiklik türevsel eylemi etkilemez. Bunun nedeni, algoritmanın sayısallaştırılmış versiyonunun ayar noktası değiştirildiğinde istenmeyen büyük bir ani yükselme üretmesidir. Ayar noktası sabitse, PV'deki değişiklikler hatadaki değişikliklerle aynı olacaktır. Bu nedenle, bu değişiklik kontrolörün proses bozukluklarına yanıt verme biçiminde hiçbir fark yaratmaz. ⓘ
Oransal eylemin PV'ye dayandırılması
Çoğu ticari kontrol sistemi, oransal eylemi yalnızca proses değişkenine dayandırma seçeneği de sunar. Bu, ayar noktasındaki değişikliklere yalnızca integral eylemin yanıt verdiği anlamına gelir. Algoritmada yapılan değişiklik, kontrolörün proses bozukluklarına yanıt verme şeklini etkilemez. Oransal eylemin PV'ye dayandırılması, ayar noktasındaki ani bir değişikliğin neden olduğu çıkıştaki anlık ve muhtemelen çok büyük değişikliği ortadan kaldırır. Sürece ve ayarlamaya bağlı olarak bu, bir ayar noktası adımına verilen yanıt için faydalı olabilir.
King etkili bir grafik tabanlı yöntem tanımlamaktadır. ⓘ
Laplace formu
Bazen PID regülatörünü Laplace dönüşümü formunda yazmak faydalı olabilir:
PID kontrolörünün Laplace formunda yazılması ve kontrol edilen sistemin transfer fonksiyonuna sahip olunması, sistemin kapalı döngü transfer fonksiyonunun belirlenmesini kolaylaştırır. ⓘ
Seri/etkileşimli form
PID kontrolörünün bir başka gösterimi de seri veya etkileşimli formdur
Burada parametreler standart formun parametreleri ile şu şekilde ilişkilidir
- , ve
ile
- . ⓘ
Bu form esasen seri olarak bir PD ve PI kontrolöründen oluşur. İntegral, kontrolörün öngerilimini hesaplamak için gerekli olduğundan, bu form, çoklu kontrolör gelişmiş kontrol şemalarının uygun şekilde uygulanması için kullanılması gereken harici bir öngerilim değerini izleme yeteneği sağlar. ⓘ
Ayrık uygulama
Bir mikrodenetleyici (MCU) veya FPGA cihazında bir PID denetleyicisinin dijital uygulamasını tasarlamak için yapılan analiz, PID denetleyicisinin standart formunun ayrıklaştırılmasını gerektirir. Birinci dereceden türevler için yaklaşımlar geriye doğru sonlu farklar ile yapılır. ve örnekleme periyodu ile ayrıklaştırılır k örnek indeksidir. ⓘ
Newton notasyonu kullanılarak PID denkleminin her iki tarafının türevi alınır: ⓘ
Türev terimleri şu şekilde yaklaştırılır,
Evet, ⓘ
Geriye doğru fark tekrar uygulandığında, ⓘ
Yukarıdaki denklemin terimlerinin basitleştirilmesi ve yeniden gruplandırılmasıyla, ayrıklaştırılmış PID kontrolörünün bir MCU'da uygulanması için bir algoritma elde edilir:
veya:
s.t. ⓘ
Not: Bu yöntem aslında şunları çözer nerede Bu sabit, düzenleme döngüsü üzerinde bir başlatma ve durdurma kontrolüne sahip olmak istediğinizde kullanışlıdır. Örneğin, Kp, Ki ve Kd değerlerini 0'a ayarlamak u(t) değerini sabit tutacaktır. Aynı şekilde, u(t) sıfır değilken hatanın zaten 0'a yakın olduğu bir sistemde bir düzenleme başlatmak istediğinizde, çıkışın 0'a gönderilmesini önler. ⓘ
Sözde kod
İşte meslekten olmayanlar tarafından kolayca anlaşılabilecek çok basit ve açık bir sözde kod grubu:
- Kp - oransal kazanç
- Ki - integral kazanç
- Kd - türev kazancı
- dt - döngü aralığı süresi ⓘ
previous_error := 0
integral := 0
döngü:
hata := ayar noktası - ölçülen_değer
orantılı := hata;
integral := integral + hata × dt
türev := (hata - önceki_hata) / dt
çıktı := Kp × oransal + Ki × integral + Kd × türev
previous_error := hata
wait(dt)
goto döngüsü ⓘ
İşte bir PID algoritmasını uygulayan daha karmaşık ve çok daha az açık bir yazılım döngüsü:
A0 := Kp + Ki*dt + Kd/dt
A1 := -Kp - 2*Kd/dt
A2 := Kd/dt
hata[2] := 0 // e(t-2)
hata[1] := 0 // e(t-1)
hata[0] := 0 // e(t)
output := u0 // Genellikle aktüatörün mevcut değeri ⓘ
döngü:
hata[2] := hata[1]
hata[1] := hata[0]
hata[0] := ayar noktası - ölçülen_değer
çıktı := çıktı + A0 * hata[0] + A1 * hata[1] + A2 * hata[2]
wait(dt)
goto döngüsü ⓘ
Burada, Kp boyutsuz bir sayıdır, Ki ise şu şekilde ifade edilir Aktüatör ve ölçülen değerin aynı birimde olmadığı bir düzenleme yapılırken (örneğin, bir valfi kontrol eden bir motor kullanarak sıcaklık düzenlemesi), Kp, Ki ve Kd bir birim dönüştürme faktörü ile düzeltilebilir. Ki'yi karşılıklı formunda (entegrasyon süresi) kullanmak da ilginç olabilir. Yukarıdaki uygulama, bazı durumlarda yararlı olabilecek bir I-sadece kontrolör gerçekleştirmeye izin verir. ⓘ
Gerçek dünyada bu, D'den A'ya dönüştürülür ve kontrol altındaki sürece manipüle edilen değişken (MV) olarak aktarılır. Mevcut hata bir sonraki farklılaşmada yeniden kullanılmak üzere başka bir yerde saklanır, program daha sonra başlangıçtan bu yana dt saniye geçene kadar bekler ve döngü yeniden başlar, PV ve ayar noktası için yeni değerler okunur ve hata için yeni bir değer hesaplanır. ⓘ
Gerçek kod için "wait(dt)" kullanımının uygun olmayabileceğini unutmayın çünkü döngü sırasında algoritmanın kendisi tarafından harcanan zamanı veya daha da önemlisi algoritmayı geciktiren herhangi bir ön işlemi hesaba katmaz. ⓘ
Kullanırken sık karşılaşılan bir sorun aşağıda gösterildiği gibi ayar noktasının yükselen veya düşen kenarının türevine verilen yanıttır:

Tipik bir geçici çözüm, zaman sabitinin alçak geçiren bir filtresini kullanarak türev eylemini filtrelemektir nerede :
Türev için Sonsuz dürtü yanıtı filtresi kullanan yukarıdaki algoritmanın bir çeşidi:
A0 := Kp + Ki*dt
A1 := -Kp
hata[2] := 0 // e(t-2)
hata[1] := 0 // e(t-1)
hata[0] := 0 // e(t)
output := u0 // Genellikle aktüatörün mevcut değeri
A0d = Kd/dt
A1d = - 2,0*Kd/dt
A2d = Kd/dt
N := 5
tau := Kd / (Kp*N) // IIR filtre zaman sabiti
alpha = dt / (2*tau)
d0 := 0
d1 := 0
fd0 := 0
fd1 := 0
döngü:
hata[2] := hata[1]
hata[1] := hata[0]
hata[0] := ayar noktası - ölçülen_değer
// PI
çıktı := çıktı + A0 * hata[0] + A1 * hata[1]
// Filtrelenmiş D
d1 = d0
d0 = A0d * hata[0] + A1d * hata[1] + A2d * hata[2]
fd1 = fd0
fd0 = ((alpha) / (alpha + 1)) * (d0 + d1) - ((alpha - 1) / (alpha + 1)) * fd1
çıktı := çıktı + fd0
wait(dt)
goto döngüsü ⓘ








































































![{\displaystyle u(t_{k})=u(t_{k-1})+K_{p}\left[\left(1+{\dfrac {\Delta t}{T_{i}}}+{\dfrac {T_{d}}{\Delta t}}\right)e(t_{k})+\left(-1-{\dfrac {2T_{d}}{\Delta t}}\right)e(t_{k-1})+{\dfrac {T_{d}}{\Delta t}}e(t_{k-2})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71fa41e1c58fcef6f2a3a4118577458ce29c659)





