Kütle

Fizikte, kütle, Newton'un ikinci yasasından yararlanılarak tanımlandığında cismin herhangi bir kuvvet tarafından ivmelenmeye karşı gösterdiği dirençtir. Doğal olarak kütlesi olan bir cisim eylemsizliğe sahiptir. Kütleçekim kuramına göre, kütle kütleçekim etkileşmesinin büyüklüğünü de belirleyen bir çarpandır(parametredir) ve eşdeğerlik ilkesinden yola çıkılarak bir cismin kütlesi kütleçekimden elde edilebilir. Ama kütle ve ağırlık birbirinden farklı kavramlardır. Ağırlık cismin hangi cisim tarafından kütleçekime maruz kaldığına göre ve konumuna göre değişebilir. ⓘ

Aynı zamanda Einstein'ın $E=mc^{2}$ yasasına göre kütle enerji olarak da değerlendirilebilir veya enerji kütle olarak da düşünülebilir. Bu durum ışığın kütleçekim yasasından etkilenmesinde yatan temel sebebi oluşturur. Işığın enerjisi kütle olarak da düşünülebilir ama Einstein'ın genel görelilik kuramına göre hesaplamalar yapılmaktadır ve bunlar oldukça karmaşık denklemlerdir. $E=mc^{2}$ yasası çerçevesinde düşündüğümüzde bir gözlemci çerçevesinde enerji olarak değerlendirilen durumun, başka bir gözlemci çerçevesinde kütle olarak değerlendirilebileceği sonucuna ulaşabiliriz. ⓘ

Kütleyi ölçmek için kullanılan birim kilogramdır. Kütleyi doğrudan ölçmek zordur. Bu yüzden kütleyi ölçmek için eşit kollu terazi kullanılır. Ayrıca cismin ilk olarak ağırlığını yaylı kantarla ölçüp daha sonra kütlesini hesaplayabiliriz. İnsanların günlük hayattaki kullanımları düşünüldüğünde, kütle bir cismin sahip olduğu madde miktarı şeklinde de tanımlanabilir. Ayrıca yüksek enerji fiziğinde, kütle cismin durağan kabul edildiği bir sistemde kendi gözlemci çerçevesinde o cismin sahip olduğu toplam enerji şeklinde düşünülür. Ama atom altı parçacıklar düşünüldüğünde temel parçacıkların, elektron veya kuark gibi, henüz nedeni bilinmeyen bir kütleye sahip oldukları görülür. Higgs parçacığı bu kütlenin nedeni olarak düşünülmektedir ama bu işle ilgili farklı kuramlar olmakla birlikte henüz tam olarak bu durumun nasıl olduğu açıklığa kavuşmamıştır ve güncel olarak çalışılan konulardan biridir. ⓘ

Kütleyi ölçmek konusunda birçok farklı görüngü vardır. Bazı teorisyenler bu görüngüleri çözmeye çalışmasına rağmen bu görüngüler (fenomenler) başka görüngüleri (fenomenleri) ortaya çıkarmıştır. Şu an denenen deneylerde aşağıdakilerden farklı olarak kütleyi ölçmenin bir yolunu bulamamışlardır: Eylemsizlik kütlesi, bir maddenin hızındaki değişimine (ivmelenmeye) gösterdiği dirençtir. Aktif kütleçekim kütlesi, kütleçekim kuvvetine sebep olan maddenin kütleçekimde sağladığı çarpanın ifadesidir. Pasif kütleçekim kütlesi, maddenin kütleçekim kuvvetinin etkisi altında kalmasına sebep olan büyüklüğüdür. ⓘ

Kütle-enerji ölçümünde cismin kütlesine karşılık gelen enerji $E=mc^{2}$ formülü kullanılarak hesaplanır. ⓘ

Bir cismin kütlesi, cisme belli bir kuvvet uygulandığında cismin ivmesini bulmamıza yardım eder. Bu görüngü eylemsizlik olarak adlandırılır. Newton’un ikinci yasasına göre, eğer herhangi bir cismin kütlesine $m$, cisme uygulanan kuvvete $F$, ivmesini de $a$ olarak ele alırsak $a=F/m$ olarak hesaplama yapabiliriz. Bir cismin kütlesi o cismin kütleçekim alanından ne kadar etkileneceğini belirler. Eğer ilk cismin kütlesine $m_{a}$, ikinci cismin kütlesine $m_{b}$, iki cismin merkezleri arasındaki uzaklığa da $r$ dersek iki cisim arasındaki çekim kuvvetini (F), F_g = Gm_am_b/r² formülünü kullanarak hesaplayabiliriz ( $G=6.67\times 10^{-11}Nm^{2}kg^{-2}$,kütleçekim sabiti). 17. yüzyıldan beri yapılan deneylerde kütleçekim kütlesi ve eylemsizlik kütlesi arasında bir fark bulunamamıştır. Bu deneylerde en yüksek hassasiyet $5\times 10^{-14}$ düzeyindedir, başka bir deyişle $10^{14}$ de 5 seviyesine kadar kütleçekim kütlesi ve eylemsizlik kütlesi aynıdır. ⓘ

Kütle ⓘ
Teraziler için kullanılan 2 kg (4,4 lb) dökme demir ağırlık
Ortak semboller	m
SI birimi	kilogram
Kapsamlı mı?	Evet
Korunmuş mu?	Evet

Fenomenler

Kütleyi ölçmek için kullanılabilecek birkaç farklı olgu vardır. Bazı teorisyenler bu olguların bazılarının birbirinden bağımsız olabileceğini düşünse de, mevcut deneyler nasıl ölçüldüğüne bakılmaksızın sonuçlarda bir fark bulamamıştır:

• Eylemsiz kütle, bir nesnenin bir kuvvet tarafından hızlandırılmaya karşı direncini ölçer (F = ma ilişkisi ile temsil edilir).
• Aktif yerçekimsel kütle, bir nesne tarafından oluşturulan yerçekimsel alanın gücünü belirler.
• Pasif yerçekimi kütlesi, bilinen bir yerçekimi alanında bir nesneye uygulanan yerçekimi kuvvetini ölçer. ⓘ

Bir nesnenin kütlesi, uygulanan bir kuvvetin varlığında ivmesini belirler. Eylemsizlik ve eylemsizlik kütlesi, fiziksel cisimlerin bu özelliğini sırasıyla niteliksel ve niceliksel düzeyde tanımlar. Newton'un ikinci hareket yasasına göre, sabit m kütleli bir cisim tek bir F kuvvetine maruz kalırsa, a ivmesi F/m ile verilir. Bir cismin kütlesi aynı zamanda bir yerçekimi alanı oluşturma ve bu alandan etkilenme derecesini de belirler. Eğer mA kütleli birinci cisim, mB kütleli ikinci cisimden r uzaklığına (kütle merkezinden kütle merkezine) yerleştirilirse, her cisim Fg = GmAmB/r² çekici kuvvetine maruz kalır; burada G = 6.67×10-11 N⋅kg-2⋅m² "evrensel çekim sabiti "dir. Bu bazen yerçekimsel kütle olarak da adlandırılır. Eylemsizlik ve yerçekimi kütlesinin özdeş olduğu 17. yüzyıldan beri tekrarlanan deneylerle gösterilmiştir; 1915'ten beri bu gözlem genel göreliliğin eşdeğerlik ilkesine a priori olarak dahil edilmiştir. ⓘ

Kütle birimleri

Kilogram, yedi SI temel biriminden biridir. ⓘ

Uluslararası Birimler Sistemi (SI) kütle birimi kilogramdır (kg). Kilogram 1000 gramdır (g) ve ilk olarak 1795 yılında buzun erime noktasındaki bir desimetre küp suyun kütlesi olarak tanımlanmıştır. Ancak, belirtilen sıcaklık ve basınçta bir desimetre küp suyun hassas ölçümü zor olduğundan, 1889'da kilogram metal bir nesnenin kütlesi olarak yeniden tanımlandı ve böylece metreden ve suyun özelliklerinden bağımsız hale geldi. 1793'te mezarın bakır prototipi, 1799'da platin Kilogramme des Archives ve 1889'da platin-iridyum Uluslararası Kilogram Prototipi (IPK). ⓘ

Ancak IPK'nın ve ulusal kopyalarının kütlesinin zaman içinde değiştiği tespit edilmiştir. Kilogramın ve diğer bazı birimlerin yeniden tanımlanması, Kasım 2018'de CGPM tarafından yapılan nihai oylamanın ardından 20 Mayıs 2019'da yürürlüğe girmiştir. Yeni tanım sadece doğanın değişmez niceliklerini kullanmaktadır: ışık hızı, sezyum hiperfine frekansı, Planck sabiti ve temel yük. ⓘ

SI birimleriyle birlikte kullanılması kabul edilen SI dışı birimler şunlardır:

• ton (t) (veya "metrik ton"), 1000 kg'a eşittir
• kütle-enerji eşdeğerliği yoluyla kütleyi eV/c² birimlerinde ifade etmek için kullanılan bir enerji birimi olan elektronvolt (eV)
• dalton (Da), serbest bir karbon-12 atomunun kütlesinin 1/12'sine eşittir, yaklaşık 1,66×10-27 kg. ⓘ

SI sistemi dışında, diğer kütle birimleri şunları içerir:

• sümüklü böcek (sl), bir İmparatorluk kütle birimi (yaklaşık 14,6 kg)
• bir kütle birimi (yaklaşık 0,45 kg) olan pound (lb), bir kuvvet birimi olan benzer şekilde adlandırılmış pound (kuvvet) (yaklaşık 4,5 N) ile birlikte kullanılır
• Planck kütlesi (yaklaşık 2,18×10-8 kg), temel sabitlerden türetilen bir niceliktir
• güneş kütlesi (M_☉), Güneş'in kütlesi olarak tanımlanır, öncelikle astronomide yıldızlar veya galaksiler gibi büyük kütleleri karşılaştırmak için kullanılır (≈ 1,99×10³⁰ kg)
• ters Compton dalga boyu ile tanımlanan bir parçacığın kütlesi (1 cm-1 ≘ 3,52×10-41 kg)
• Schwarzschild yarıçapı (1 cm ≘ 6,73×10²⁴ kg) ile tanımlanan bir yıldızın veya kara deliğin kütlesi. ⓘ

Tanımlar

Fizik biliminde, kavramsal olarak kütlenin en az yedi farklı yönü veya kütle kavramını içeren yedi fiziksel kavram arasında ayrım yapılabilir. Bugüne kadar yapılan her deney bu yedi değerin orantılı ve bazı durumlarda eşit olduğunu göstermiştir ve bu orantılılık soyut kütle kavramını ortaya çıkarmıştır. Kütlenin ölçülebileceği veya operasyonel olarak tanımlanabileceği birkaç yol vardır:

• Eylemsiz kütle, bir kuvvet uygulandığında bir nesnenin ivmelenmeye karşı direncinin bir ölçüsüdür. Bir nesneye bir kuvvet uygulayarak ve bu kuvvetten kaynaklanan ivmeyi ölçerek belirlenir. Küçük eylemsizlik kütlesine sahip bir cisim, aynı kuvvet uygulandığında büyük eylemsizlik kütlesine sahip bir cisimden daha fazla hızlanacaktır. Daha büyük kütleli cismin daha büyük eylemsizliğe sahip olduğu söylenir.
• Aktif yerçekimsel kütle, bir cismin yerçekimsel akısının gücünün bir ölçüsüdür (yerçekimsel akı, çevreleyen bir yüzey üzerindeki yerçekimsel alanın yüzey integraline eşittir). Yerçekimi alanı, küçük bir "test nesnesinin" serbestçe düşmesine izin vererek ve serbest düşüş ivmesini ölçerek ölçülebilir. Örneğin, Ay'ın yakınında serbest düşüşte olan bir nesne daha küçük bir çekim alanına maruz kalır ve dolayısıyla aynı nesne Dünya'nın yakınında serbest düşüşte olsaydı olacağından daha yavaş hızlanır. Ay'ın yakınındaki yerçekimi alanı daha zayıftır çünkü Ay daha az aktif yerçekimi kütlesine sahiptir.
• Pasif yerçekimi kütlesi, bir nesnenin yerçekimi alanıyla etkileşiminin gücünün bir ölçüsüdür. Pasif yerçekimi kütlesi, bir nesnenin ağırlığının serbest düşme ivmesine bölünmesiyle belirlenir. Aynı yerçekimi alanı içindeki iki nesne aynı ivmeyi deneyimleyecektir; ancak, daha küçük pasif yerçekimi kütlesine sahip nesne, daha büyük pasif yerçekimi kütlesine sahip nesneden daha küçük bir kuvvet (daha az ağırlık) deneyimleyecektir.
• Kütle-enerji eşdeğerliği ilkesine göre enerjinin de kütlesi vardır. Bu eşdeğerlik, çift üretimi, nükleer füzyon ve ışığın yerçekimsel bükülmesi gibi çok sayıda fiziksel süreçte örneklendirilmiştir. Çift üretimi ve nükleer füzyon, ölçülebilir miktarlarda kütlenin enerjiye dönüştürüldüğü ya da tam tersinin gerçekleştiği süreçlerdir. Işığın yerçekimsel bükülmesinde, saf enerji fotonlarının pasif yerçekimsel kütleye benzer bir davranış sergilediği gösterilmiştir.
• Uzayzamanın eğriliği kütlenin varlığının göreceli bir tezahürüdür. Bu tür bir eğrilik son derece zayıftır ve ölçülmesi zordur. Bu nedenle eğrilik, Einstein'ın genel görelilik teorisi tarafından öngörülene kadar keşfedilememiştir. Örneğin, Dünya yüzeyindeki son derece hassas atomik saatlerin, uzaydaki benzer saatlere kıyasla daha az zaman ölçtüğü (daha yavaş çalıştığı) bulunmuştur. Geçen zamandaki bu fark, yerçekimsel zaman genişlemesi adı verilen bir eğrilik biçimidir. Eğriliğin diğer biçimleri Gravity Probe B uydusu kullanılarak ölçülmüştür.
• Kuantum kütlesi, bir nesnenin kuantum frekansı ile dalga sayısı arasındaki fark olarak kendini gösterir. Bir parçacığın kuantum kütlesi ters Compton dalga boyuyla orantılıdır ve çeşitli spektroskopi biçimleriyle belirlenebilir. Rölativistik kuantum mekaniğinde kütle, Poincaré grubunun indirgenemez temsil etiketlerinden biridir. ⓘ

Ağırlık ve kütle

Günlük kullanımda, kütle ve "ağırlık" genellikle birbirinin yerine kullanılır. Örneğin, bir kişinin ağırlığı 75 kg olarak ifade edilebilir. Sabit bir yerçekimi alanında, bir nesnenin ağırlığı kütlesiyle orantılıdır ve her iki kavram için de aynı birimi kullanmak sorunsuzdur. Ancak Dünya'nın çekim alanının farklı yerlerdeki gücündeki küçük farklılıklar nedeniyle, bu ayrım yüzde birkaçtan daha hassas ölçümler için ve uzay ya da diğer gezegenler gibi Dünya yüzeyinden uzak yerler için önemli hale gelir. Kavramsal olarak, "kütle" (kilogram cinsinden ölçülür) bir nesnenin içsel bir özelliğini ifade ederken, "ağırlık" (newton cinsinden ölçülür) bir nesnenin, yakındaki yerçekimi alanından etkilenebilen mevcut serbest düşüş rotasından sapmaya karşı direncini ölçer. Yerçekimi alanı ne kadar güçlü olursa olsun, serbest düşüş halindeki nesneler ağırlıksızdır, ancak yine de kütleleri vardır. ⓘ

"Ağırlık" olarak bilinen kuvvet, kütlenin serbest düşüşten farklı olarak hızlandırıldığı tüm durumlarda kütle ve ivme ile orantılıdır. Örneğin, bir cisim yerçekimi alanında hareketsizken (serbest düşme yerine), bir ölçekten ya da Dünya veya Ay gibi bir gezegensel cismin yüzeyinden gelen bir kuvvet tarafından hızlandırılmalıdır. Bu kuvvet nesnenin serbest düşüşe geçmesini engeller. Ağırlık bu gibi durumlarda karşıt kuvvettir ve bu nedenle serbest düşüş ivmesi tarafından belirlenir. Örneğin Dünya yüzeyinde 50 kilogram kütleli bir cisim 491 newton ağırlığındadır, bu da cismin serbest düşüşe geçmesini engellemek için 491 newton uygulandığı anlamına gelir. Buna karşılık, Ay'ın yüzeyinde aynı nesne hala 50 kilogramlık bir kütleye sahiptir, ancak sadece 81,5 newton ağırlığındadır, çünkü bu nesnenin Ay'da serbest düşüşe geçmesini önlemek için sadece 81,5 newton gereklidir. Matematiksel terimlerle ifade edecek olursak, Dünya yüzeyinde bir nesnenin ağırlığı W, kütlesi m ile W = mg ile ilişkilidir; burada g = 9,80665 m/s² Dünya'nın yerçekimi alanından kaynaklanan ivmedir (serbest düşen bir nesnenin maruz kaldığı ivme olarak ifade edilir). ⓘ

Nesnelerin bir gezegen yüzeyinin direnci dışındaki kuvvetlerden kaynaklanan mekanik ivmelere maruz kalması gibi diğer durumlar için ağırlık kuvveti, bir nesnenin kütlesi ile serbest düşüşten uzak toplam ivmenin çarpımı ile orantılıdır ve buna uygun ivme denir. Bu tür mekanizmalar sayesinde, asansörler, araçlar, santrifüjler ve benzerlerindeki nesneler, gezegen yüzeylerinden kaynaklanan yerçekiminin nesneler üzerindeki etkilerine karşı dirençten kaynaklanan ağırlık kuvvetlerinin kat kat fazlasına maruz kalabilir. Bu gibi durumlarda, bir nesnenin ağırlığı W için genelleştirilmiş denklem, kütlesi m ile W = -ma denklemi ile ilişkilidir; burada a, yerçekimi dışındaki tüm etkilerin neden olduğu nesnenin uygun ivmesidir. (Yine, eğer yerçekimi tek etki ise, örneğin bir nesne serbestçe düştüğünde olduğu gibi, ağırlığı sıfır olacaktır). ⓘ

Eylemsiz ve yerçekimsel kütle

Eylemsiz kütle, pasif yerçekimi kütlesi ve aktif yerçekimi kütlesi kavramsal olarak birbirinden farklı olsa da, hiçbir deney bunlar arasında herhangi bir fark olduğunu kesin olarak göstermemiştir. Klasik mekanikte, Newton'un üçüncü yasası aktif ve pasif yerçekimi kütlesinin her zaman aynı (ya da en azından orantılı) olması gerektiğini ima eder, ancak klasik teori yerçekimi kütlesinin neden eylemsizlik kütlesine eşit olması gerektiğine dair ikna edici bir neden sunmaz. Bu sadece ampirik bir gerçektir. ⓘ

Albert Einstein genel görelilik kuramını eylemsiz ve pasif kütleçekimsel kütlelerin aynı olduğu varsayımından yola çıkarak geliştirmiştir. Bu eşdeğerlik ilkesi olarak bilinir. ⓘ

Genellikle "Galile eşdeğerlik ilkesi" veya "zayıf eşdeğerlik ilkesi" olarak adlandırılan özel eşdeğerlik, serbestçe düşen nesneler için en önemli sonuca sahiptir. Bir cismin sırasıyla m ve M eylemsizlik ve kütleçekim kütlelerine sahip olduğunu varsayalım. Eğer cisme etki eden tek kuvvet g kütleçekim alanından geliyorsa, cisim üzerindeki kuvvet g'dir:

$F=Mg.$ ⓘ

Bu kuvvet göz önüne alındığında, nesnenin ivmesi Newton'un ikinci yasası ile belirlenebilir:

$F=ma.$ ⓘ

Bunlar bir araya getirildiğinde, yerçekimi ivmesi şu şekilde verilir:

$a={\frac {M}{m}}g.$ ⓘ

Bu, herhangi bir nesnenin yerçekimsel kütlesinin eylemsiz kütlesine oranının, ancak ve ancak tüm nesneler belirli bir yerçekimi alanında aynı oranda düşüyorsa, bazı K sabitine eşit olduğunu söyler. Bu olgu "serbest düşüşün evrenselliği" olarak adlandırılır. Buna ek olarak, birimlerimizi uygun şekilde tanımlayarak K sabiti 1 olarak alınabilir. ⓘ

Serbest düşmenin evrenselliğini gösteren ilk deneyler -bilimsel 'folklor'a göre- Galileo tarafından Pisa Kulesi'nden cisimler düşürülerek gerçekleştirilmiştir. Bu büyük olasılıkla uydurmadır: Galileo'nun deneylerini, hareketi yavaşlatmak ve zamanlama doğruluğunu artırmak için neredeyse sürtünmesiz eğik düzlemlerden aşağı yuvarlanan toplarla gerçekleştirmiş olması daha olasıdır. Loránd Eötvös tarafından 1889'da burulma dengesi sarkacı kullanılarak yapılanlar gibi giderek daha hassas deneyler gerçekleştirilmiştir. 2008 yılı itibariyle, en azından 10-6 hassasiyetle, evrensellikten ve dolayısıyla Galile denkliğinden herhangi bir sapma bulunamamıştır. Daha hassas deneysel çalışmalar halen devam etmektedir. ⓘ

Astronot David Scott Ay'da tüy ve çekiç düşürme deneyini gerçekleştiriyor ⓘ

Serbest düşüşün evrenselliği yalnızca yerçekiminin tek etkili kuvvet olduğu sistemler için geçerlidir. Diğer tüm kuvvetlerin, özellikle de sürtünme ve hava direncinin olmaması ya da en azından ihmal edilebilir düzeyde olması gerekir. Örneğin, bir çekiç ve bir tüy Dünya üzerinde aynı yükseklikten havaya bırakılırsa, tüyün yere ulaşması çok daha uzun sürecektir; tüy gerçekten serbest düşüşte değildir çünkü tüye karşı yukarı doğru hava direnci kuvveti, aşağı doğru yerçekimi kuvvetiyle karşılaştırılabilir. Öte yandan, deney hava direncinin olmadığı bir vakum ortamında gerçekleştirilirse, çekiç ve tüy yere tam olarak aynı anda çarpmalıdır (her iki nesnenin birbirine ve yerin her iki nesneye doğru ivmesinin ihmal edilebilir olduğu varsayılırsa). Bu, bir lise laboratuvarında, nesneleri vakum pompasıyla havası alınmış şeffaf tüplere bırakarak kolayca yapılabilir. David Scott'ın Apollo 15 sırasında Ay yüzeyinde yaptığı gibi, doğal olarak vakumlu bir ortamda yapıldığında daha da dramatiktir. ⓘ

Einstein eşdeğerlik ilkesi ya da güçlü eşdeğerlik ilkesi olarak bilinen eşdeğerlik ilkesinin daha güçlü bir versiyonu, genel görelilik kuramının temelinde yatmaktadır. Einstein'ın eşdeğerlik ilkesi, uzay-zamanın yeterince küçük bölgelerinde, tekdüze bir ivme ile tekdüze bir kütleçekim alanını birbirinden ayırmanın imkansız olduğunu belirtir. Dolayısıyla teori, kütleli bir cisme kütleçekim alanının neden olduğu kuvvetin, cismin düz bir çizgide hareket etme eğiliminin (başka bir deyişle eylemsizliğinin) bir sonucu olduğunu ve bu nedenle eylemsiz kütlesinin ve kütleçekim alanının gücünün bir fonksiyonu olması gerektiğini varsayar. ⓘ

Köken

Teorik fizikte kütle üretim mekanizması, kütlenin kökenini fiziğin en temel yasalarından hareketle açıklamaya çalışan bir teoridir. Bugüne kadar, kütlenin kökenine ilişkin farklı görüşleri savunan bir dizi farklı model önerilmiştir. Kütle kavramının yerçekimi etkileşimiyle güçlü bir şekilde ilişkili olması, ancak Standart Model olarak bilinen parçacık fiziğinin şu anda popüler olan modeliyle bir teorinin henüz uzlaştırılamamış olması sorunu daha da karmaşık hale getirmektedir. ⓘ

Newton öncesi kavramlar

Miktar olarak ağırlık

Hunefer Papirüsü'ndeki (19. hanedanlığa tarihlenen, MÖ 1285 civarı) erken dönem terazi tasviri. Sahnede Anubis, Hunefer'in kalbini tartarken gösterilmektedir. ⓘ

Miktar kavramı çok eskidir ve kayıtlı tarihten öncesine dayanır. İnsanlar, erken bir dönemde, benzer nesnelerden oluşan bir koleksiyonun ağırlığının koleksiyondaki nesne sayısıyla doğru orantılı olduğunu fark etmişlerdir:

$W_{n}\propto n,$ ⓘ

Burada W benzer nesneler koleksiyonunun ağırlığı, n ise koleksiyondaki nesne sayısıdır. Orantılılık, tanımı gereği, iki değerin sabit bir orana sahip olduğu anlamına gelir:

${\frac {W_{n}}{n}}={\frac {W_{m}}{m}}$ya da eşdeğer olarak ${\frac {W_{n}}{W_{m}}}={\frac {n}{m}}.$ ⓘ

Bu ilişkinin ilk kullanımlarından biri, bir nesnenin ağırlığının kuvvetini başka bir nesnenin ağırlığının kuvvetine karşı dengeleyen bir terazidir. Bir terazinin iki tarafı, nesnelerin benzer yerçekimi alanlarına maruz kalmasına yetecek kadar yakındır. Dolayısıyla, benzer kütlelere sahiplerse ağırlıkları da benzer olacaktır. Bu da terazinin ağırlıkları karşılaştırarak kütleleri de karşılaştırmasını sağlar. ⓘ

Sonuç olarak, tarihsel ağırlık standartları genellikle miktar cinsinden tanımlanmıştır. Örneğin Romalılar keçiboynuzu tohumunu (karat veya siliqua) bir ölçüm standardı olarak kullanmışlardır. Eğer bir nesnenin ağırlığı 1728 keçiboynuzu tohumuna eşdeğerse, o zaman nesnenin bir Roma poundu ağırlığında olduğu söylenirdi. Öte yandan, eğer nesnenin ağırlığı 144 keçiboynuzu tohumuna eşdeğerse, o zaman nesnenin bir Roma onsu (uncia) ağırlığında olduğu söylenirdi. Roma poundu ve onsunun her ikisi de aynı ortak kütle standardı olan keçiboynuzu tohumunun farklı boyutlardaki koleksiyonları açısından tanımlanmıştır. Bir Roma onsunun (144 keçiboynuzu tohumu) bir Roma pounduna (1728 keçiboynuzu tohumu) oranı şöyleydi:

${\frac {\mathrm {ounce} }{\mathrm {pound} }}={\frac {W_{144}}{W_{1728}}}={\frac {144}{1728}}={\frac {1}{12}}.$ ⓘ

Gezegensel hareket

Milattan sonra 1600 yılında, Johannas Kepler, en hassas astronomik verilerin bazılarına sahip olan Tycho Brahe’nin yanına çalışmaya başladı. Brahe'nin hassas Mars gezegeni gözlemlerini kullanarak, Kepler, gezegensel hareketi karakterize etmek için kendi yöntemini geliştirmek adına 5 yıl çalıştı. 1609’da Kepler, gezegenlerin Güneş etrafındaki hareketini açıklayan üç yasa yayınladı. Kepler son hareket modelinde, gezegenlerin, merkezinin birinde Güneş olduğu eliptik bir yörünge etrafında nasıl hareket ettiklerini açıkladı. Kepler bir gezegenin yörüngesinin karesiyle, gezegenin yarı-büyük ekseninin küpü doğru orantılıdır ya da eşdeğerdir ve bu iki değerin oranı Güneş Sistemi’ndeki tüm gezegenler için sabittir şeklindeki üçüncü yasasını yayınlayarak bu hareketi açıklayacak en önemli adımlardan birini attı. ⓘ

25 Ağustos 1606’da Galileo Galilei, Venedikli tüccar bir gruba ilk teleskobunu gösterdi ve Ocak 1610’un öncesinde Galileo, Jüpiter'in etrafında yıldızlara benzer ama çıplak gözle görülemeyen nesneler gözlemledi. Ancak gözlemlerinden birkaç gün sonra Galileo, bu “yıldızların” Jüpiter’in yörüngesinde olduğunu fark etti. Bu dört nesne(Keşfinin onuruna Galile uyduları olarak adlandırılır) Dünya'dan gözlenen ama Dünya’nın ve Güneş’in yörüngesi dışında başka bir yörünge etrafında döndüğü fark edilen ilk cisimlerdir. Galileo, sonraki on sekiz ay içinde bu uydularını gözlemeye devam etti ve 1611’in ortalarında uyduların devirlerinin zamanı hakkında tahminlerde bulundu. Bu tahminler belli bir hassayite kadar doğru olmasına rağmen Jüpiter ve Dünya arasındaki uzaklığın değişmesinden dolayı bir miktar hata payı barındırıyordu. Daha sonra Romer tarafından bu durum, Jüpiter ile Dünya'nın arasındaki uzaklığın değişmesi, kullanılarak ilk defa ışığın hızı hesaplandı. Bu hesap 26% lik hata payı içeriyordu ama zamanına göre yapılmış en iyi hesaptı ve Romer ışık hızını 220000 km/s (saniyede 220 bin kilometre) olarak hesaplamıştı. ⓘ

Galileo'nun serbest düşüşü

Galileo Galilei (1636) ⓘ

Serbestçe düşen bir topun kat ettiği mesafe, geçen zamanın karesi ile orantılıdır ⓘ

Galileo, 1638'den bir süre önce dikkatini serbest düşüş halindeki cisimler olgusuna çevirmiş ve bu hareketleri karakterize etmeye çalışmıştır. Galileo, Dünya'nın yerçekimi alanını araştıran ilk kişi olmadığı gibi, temel özelliklerini doğru bir şekilde tanımlayan ilk kişi de değildi. Bununla birlikte, Galileo'nun fiziksel ilkeleri belirlemek için bilimsel deneylere güvenmesi, gelecek nesil bilim insanları üzerinde derin bir etkiye sahip olacaktı. Bunların sadece bir kavramı açıklamak için kullanılan varsayımsal deneyler mi yoksa Galileo tarafından gerçekleştirilen gerçek deneyler mi olduğu belirsizdir, ancak bu deneylerden elde edilen sonuçlar hem gerçekçi hem de ilgi çekicidir. Galileo'nun öğrencisi Vincenzo Viviani'nin yazdığı bir biyografide, Galileo'nun aynı malzemeden ama farklı kütlelerden topları Pisa Kulesi'nden aşağı bırakarak iniş sürelerinin kütlelerinden bağımsız olduğunu gösterdiği belirtilmektedir. Bu sonucu desteklemek için Galileo aşağıdaki teorik argümanı ileri sürmüştür: Farklı kütlelere ve farklı düşüş hızlarına sahip iki cisim bir iple bağlanırsa, birleşik sistem artık daha kütleli olduğu için mi daha hızlı düşer, yoksa daha hafif olan cisim daha ağır olan cismi daha yavaş düşüşünde tutar mı? Bu sorunun tek ikna edici çözümü, tüm cisimlerin aynı hızda düşmesi gerektiğidir. ⓘ

Daha sonraki bir deney Galileo'nun 1638'de yayınlanan İki Yeni Bilim kitabında anlatılmıştır. Galileo'nun kurgusal karakterlerinden biri olan Salviati, bronz bir top ve ahşap bir rampa kullanarak yaptığı bir deneyi anlatır. Ahşap rampa "12 arşın uzunluğunda, yarım arşın genişliğinde ve üç parmak kalınlığında" olup düz, pürüzsüz, cilalı bir oluğa sahipti. Oluk "mümkün olduğunca pürüzsüz ve cilalı bir parşömenle" kaplanmıştı. Ve bu oluğun içine "sert, pürüzsüz ve çok yuvarlak bronz bir top" yerleştirilmiştir. Rampa, geçen sürenin ölçülebilmesi için ivmeyi yeterince yavaşlatacak şekilde çeşitli açılarla eğimlendirildi. Topun rampadan aşağı bilinen bir mesafeye yuvarlanmasına izin verildi ve topun bilinen mesafeyi kat etmesi için geçen süre ölçüldü. Zaman aşağıdaki şekilde tarif edilen bir su saati kullanılarak ölçülmüştür:

"Büyük bir su kabı yüksek bir yere yerleştirildi; bu kabın dibine ince bir su püskürten küçük çaplı bir boru lehimlendi ve bu su, kanalın tüm uzunluğu ya da uzunluğunun bir kısmı boyunca her iniş sırasında küçük bir bardakta toplandı; Bu şekilde toplanan su, her inişten sonra çok hassas bir terazide tartıldı; bu ağırlıkların farkları ve oranları bize zamanların farklarını ve oranlarını verdi ve bu öyle bir doğrulukla yapıldı ki, işlem birçok kez tekrarlanmasına rağmen sonuçlarda kayda değer bir tutarsızlık olmadı. " ⓘ

Galileo, serbest düşüş halindeki bir cisim için, cismin düştüğü mesafenin her zaman geçen zamanın karesiyle orantılı olduğunu buldu:

${\text{Distance}}\propto {{\text{Time}}^{2}}$ ⓘ

Galileo, Dünya'nın çekim alanının etkisi altında serbest düşüşte olan cisimlerin sabit bir ivmeye sahip olduğunu göstermiş ve Galileo'nun çağdaşı Johannes Kepler de gezegenlerin Güneş'in çekim kütlesinin etkisi altında eliptik yollar izlediğini göstermişti. Ancak Galileo'nun serbest düşme hareketleri ile Kepler'in gezegen hareketleri Galileo'nun yaşamı boyunca farklı kalmıştır. ⓘ

Bir topun, serbest düşme esnasındaki eşit zaman aralıklarında olan yer değiştirmesi. ⓘ

Newton kütlesi

Isaac Newton 1689 ⓘ

Dünya'nın Ay'ı		Dünya'nın Kütlesi ⓘ
Yarı majör eksen	Sidereal yörünge periyodu
0,002 569 AU	0,074 802 yıldız yılı	$1.2\pi ^{2}\cdot 10^{-5}{\frac {{\text{AU}}^{3}}{{\text{y}}^{2}}}=3.986\cdot 10^{14}{\frac {{\text{m}}^{3}}{{\text{s}}^{2}}}$
Dünya'nın yerçekimi	Dünya'nın yarıçapı
9.806 65 m/s2	6 375 km

Robert Hooke 1674 yılında yerçekimi kuvvetleri kavramını yayınlamış ve tüm gök cisimlerinin kendi merkezlerine doğru bir çekim veya çekim gücüne sahip olduklarını ve aynı zamanda faaliyet alanları içinde bulunan diğer tüm gök cisimlerini de çektiklerini belirtmiştir. Ayrıca, yerçekimsel çekimin, üzerinde çalışılan cisim kendi merkezine ne kadar yakınsa o kadar arttığını belirtmiştir. Hooke, Isaac Newton ile 1679 ve 1680 yıllarında yaptığı yazışmalarda, çekim kuvvetlerinin iki cisim arasındaki mesafenin iki katına göre azalabileceği varsayımında bulunmuştur. Hooke, kalkülüsün geliştirilmesinde öncü olan Newton'u, Hooke'un hipotezinin doğru olup olmadığını belirlemek için Keplerian yörüngelerinin matematiksel detayları üzerinde çalışmaya teşvik etti. Newton'un kendi araştırmaları Hooke'un haklı olduğunu doğruladı, ancak iki adam arasındaki kişisel farklılıklar nedeniyle Newton bunu Hooke'a açıklamamayı tercih etti. Isaac Newton 1684 yılına kadar keşifleri konusunda sessiz kaldı ve bu tarihte bir arkadaşı olan Edmond Halley'e yerçekimsel yörüngeler sorununu çözdüğünü ancak çözümü ofisinde unuttuğunu söyledi. Halley tarafından teşvik edilen Newton, yerçekimiyle ilgili fikirlerini geliştirmeye ve tüm bulgularını yayınlamaya karar verdi. Kasım 1684'te Isaac Newton, Edmund Halley'e şimdi kayıp olan ancak De motu corporum in gyrum (Latince "Bir yörüngedeki cisimlerin hareketi üzerine") başlıklı olduğu tahmin edilen bir belge gönderdi. Halley, Newton'un bulgularını Londra Kraliyet Cemiyeti'ne sundu ve bunu daha kapsamlı bir sunumun izleyeceği sözünü verdi. Newton daha sonra fikirlerini Philosophiæ Naturalis Principia Mathematica (Latince: Doğa Felsefesinin Matematiksel İlkeleri) başlıklı üç kitaplık bir set halinde kaydetti. İlki 28 Nisan 1685-86'da, ikincisi 2 Mart 1686-87'de ve üçüncüsü 6 Nisan 1686-87'de Royal Society tarafından kabul edildi. Kraliyet Cemiyeti Newton'un tüm koleksiyonunu masrafları kendisine ait olmak üzere Mayıs 1686-87'de yayınladı. ⓘ

Isaac Newton, Kepler'in yerçekimsel kütlesi ile Galileo'nun yerçekimsel ivmesi arasındaki boşluğu doldurmuş ve her ikisini de yöneten aşağıdaki ilişkiyi keşfetmiştir:

$\mathbf {g} =-\mu {\frac {\hat {\mathbf {R} }}{|\mathbf {R} |^{2}}}$ ⓘ

Burada g, yerçekimi alanlarının bulunduğu bir uzay bölgesinden geçerken bir cismin görünürdeki ivmesi, μ yerçekimi alanlarına neden olan cismin yerçekimi kütlesi (standart yerçekimi parametresi) ve R radyal koordinattır (iki cismin merkezleri arasındaki mesafe). ⓘ

Newton, bir cismin yerçekimi kütlesi ile yerçekimi alanı arasındaki kesin ilişkiyi bularak, yerçekimi kütlesini ölçmek için ikinci bir yöntem sağlamıştır. Dünya'nın kütlesi Kepler'in yöntemi kullanılarak (Ay'ın yörüngesinden) belirlenebileceği gibi, Dünya'nın yüzeyindeki yerçekimi ivmesinin ölçülmesi ve bunun Dünya'nın yarıçapının karesiyle çarpılmasıyla da belirlenebilir. Dünya'nın kütlesi yaklaşık olarak Güneş'in kütlesinin milyonda üçü kadardır. Bugüne kadar yerçekimi kütlesini ölçmek için başka doğru bir yöntem keşfedilmemiştir. ⓘ

Newton, Kepler'in kütleçekimsel kütle ve Galileo'nun kütleçekimsel ivme kavramları arasındaki boşluğu dolduran

$\mathbf {g} =-\mu {\frac {\hat {\mathbf {R} }}{|\mathbf {R} |^{2}}}$

bağıntıyı ispatladı. Bu denklemde g kütleçekimden etkilenen cismin gözlemlenen ivmesine, μ kütleçekime sebep olan cismin kütleçekimsel kütlesine ve R etkileşimde bulunan iki cismin merkezleri arasındaki uzunluğa karşılık gelmektedir. ⓘ

Newton'un güllesi

Çok yüksek bir dağın tepesindeki bir top, yatay olarak bir gülle fırlatır. Hız düşükse, gülle hızla Dünya'ya geri düşer (A, B). Orta hızlarda, eliptik bir yörünge boyunca Dünya'nın etrafında dönecektir (C, D). Kaçış hızının ötesinde, geri dönmeden Dünya'yı terk edecektir (E). ⓘ

Newton'un güllesi, Galileo'nun yerçekimi ivmesi ile Kepler'in eliptik yörüngeleri arasındaki boşluğu doldurmak için kullanılan bir düşünce deneyiydi. Newton'un 1728 tarihli A Treatise of the System of the World adlı kitabında yer almıştır. Galileo'nun yerçekimi kavramına göre, düşürülen bir taş sabit bir ivmeyle Dünya'ya doğru düşer. Ancak Newton, bir taş yatay olarak atıldığında (yani yanlamasına ya da Dünya'nın yerçekimine dik olarak) kavisli bir yol izlediğini açıklar. "Çünkü fırlatılan bir taş, kendi ağırlığının baskısıyla, yalnızca fırlatılışıyla izlemesi gereken doğrusal yoldan çıkmaya zorlanır ve havada eğri bir çizgi çizmeye zorlanır; ve bu eğri yoldan sonunda yere indirilir. Ve yansıtıldığı hız ne kadar büyükse, Dünya'ya düşmeden önce o kadar uzağa gider." Newton ayrıca, eğer bir cisim "yüksek bir dağın tepesinden yatay bir yönde" yeterli bir hızla fırlatılırsa, "sonunda Dünya'nın çevresinin oldukça ötesine ulaşacağını ve fırlatıldığı dağa geri döneceğini" söyler. ⓘ

Evrensel yerçekimi kütlesi

Bir elma Dünya'nın her yerine doğru yönelen yerçekimi alanlarına maruz kalır; ancak bu birçok alanın toplamı Dünya'nın merkezine doğru yönelen tek bir yerçekimi alanı oluşturur ⓘ

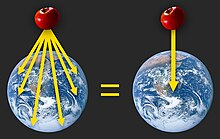
Göklerin tamamen farklı malzemelerden yapıldığını belirten daha önceki teorilerin (örneğin gök küreleri) aksine, Newton'un kütle teorisi kısmen evrensel yerçekimi kütlesini ortaya koyduğu için çığır açıcı olmuştur: her nesnenin yerçekimi kütlesi vardır ve bu nedenle her nesne bir yerçekimi alanı oluşturur. Newton ayrıca her nesnenin çekim alanının gücünün, o nesneye olan uzaklığın karesine göre azalacağını varsaymıştır. Eğer küçük cisimlerden oluşan büyük bir koleksiyon Dünya ya da Güneş gibi dev bir küresel cisme dönüşürse, Newton bu koleksiyonun cismin toplam kütlesiyle orantılı ve cismin merkezine olan uzaklığın karesiyle ters orantılı bir çekim alanı yaratacağını hesaplamıştır. ⓘ

Örneğin, Newton'un evrensel çekim teorisine göre, her keçiboynuzu tohumu bir çekim alanı üretir. Bu nedenle, eğer çok sayıda keçiboynuzu tohumu toplanıp muazzam bir küre haline getirilirse, kürenin çekim alanı küredeki keçiboynuzu tohumu sayısıyla orantılı olacaktır. Dolayısıyla, Dünya veya Güneş'inkine benzer bir çekim alanı oluşturmak için gerekli olan keçiboynuzu tohumu sayısını tam olarak belirlemek teorik olarak mümkün olmalıdır. Aslında, birim dönüştürme yoluyla, herhangi bir geleneksel kütle biriminin teorik olarak yerçekimi kütlesini ölçmek için kullanılabileceğini anlamak basit bir soyutlama meselesidir. ⓘ

Cavendish'in burulmalı terazi aletinin, içinde bulunduğu binayı da içeren dikey kesit çizimi. Büyük bilyeler bir çerçeveye asılmıştı, böylece dışarıdan bir makara ile küçük bilyelerin yanındaki pozisyona döndürülebiliyorlardı. Cavendish'in makalesinden Şekil 1. ⓘ

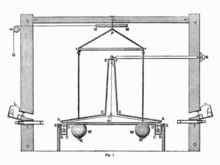
Yerçekimsel kütlenin geleneksel kütle birimleri cinsinden ölçülmesi prensipte basit, ancak pratikte son derece zordur. Newton'un teorisine göre, tüm nesneler yerçekimi alanları üretir ve teorik olarak çok sayıda küçük nesneyi bir araya getirmek ve bunları yerçekimi yapan muazzam bir küre haline getirmek mümkündür. Ancak pratik açıdan bakıldığında, küçük nesnelerin çekim alanları son derece zayıftır ve ölçülmesi zordur. Newton'un evrensel çekimle ilgili kitapları 1680'lerde yayınlandı, ancak Dünya'nın kütlesinin geleneksel kütle birimleri cinsinden ilk başarılı ölçümü, Cavendish deneyi, yüz yıldan fazla bir süre sonra, 1797'ye kadar gerçekleşmedi. Henry Cavendish, Dünya'nın yoğunluğunun suyun yoğunluğunun 5,448 ± 0,033 katı olduğunu bulmuştur. 2009 yılı itibariyle, Dünya'nın kilogram cinsinden kütlesi yalnızca beş basamaklı doğrulukla bilinirken, yerçekimi kütlesi dokuzdan fazla anlamlı rakamla bilinmektedir. ⓘ

MA ve MB kütlelerine sahip, R_AB yer değiştirmesi ile ayrılmış iki A ve B cismi verildiğinde, Newton'un çekim yasası her bir cismin diğerine şu büyüklükte bir çekim kuvveti uyguladığını belirtir

$\mathbf {F} _{\text{AB}}=-GM_{\text{A}}M_{\text{B}}{\frac {{\hat {\mathbf {R} }}_{\text{AB}}}{|\mathbf {R} _{\text{AB}}|^{2}}}\$,

Burada G evrensel yerçekimi sabitidir. Yukarıdaki ifade şu şekilde yeniden formüle edilebilir: g yerçekimi alanında belirli bir konumdaki büyüklük ise, yerçekimi kütlesi M olan bir nesne üzerindeki yerçekimi kuvveti

$F=Mg$.

Bu, kütlelerin tartılarak belirlendiği temeldir. Örneğin basit yaylı terazilerde, Hooke yasası uyarınca F kuvveti, tartı kefesinin altındaki yayın yer değiştirmesiyle orantılıdır ve teraziler g'yi hesaba katacak şekilde kalibre edilerek M kütlesinin okunmasına olanak tanır. Yerçekimi alanının terazinin her iki tarafında da eşdeğer olduğu varsayıldığında, bir terazi göreli ağırlığı ölçerek her bir nesnenin göreli yerçekimi kütlesini verir. ⓘ

Eylemsiz kütle

Kütle ölçer, ağırlıksız ortamda bir astronotun atalet kütlesini ölçmeye yarayan bir cihaz. Kütle, astronotun bağlı olduğu bir yayın salınım periyodu üzerinden hesaplanır (Tsiolkovsky Devlet Kozmonotik Tarihi Müzesi) ⓘ

Eylemsiz kütle, bir nesnenin ivmeye karşı gösterdiği dirençle ölçülen kütlesidir. Bu tanım Ernst Mach tarafından savunulmuş ve o zamandan beri Percy W. Bridgman tarafından işlemselcilik kavramına dönüştürülmüştür. Kütlenin basit klasik mekanik tanımı, özel görelilik teorisindeki tanımdan biraz farklıdır, ancak temel anlamı aynıdır. ⓘ

Klasik mekanikte, Newton'un ikinci yasasına göre, bir cismin herhangi bir zaman anında hareket denklemine uyması halinde m kütlesine sahip olduğunu söyleriz ⓘ

$\mathbf {F} =m\mathbf {a} ,$ ⓘ

Burada F cisme etki eden bileşke kuvvet, a ise cismin kütle merkezinin ivmesidir. Şimdilik, "cisme etki eden kuvvetin" gerçekte ne anlama geldiği sorusunu bir kenara bırakacağız. ⓘ

Bu denklem, kütlenin bir cismin eylemsizliği ile nasıl ilişkili olduğunu göstermektedir. Farklı kütlelere sahip iki cisim düşünün. Her birine aynı kuvveti uygularsak, daha büyük kütleli cisim daha küçük bir ivme yaşayacak ve daha küçük kütleli cisim daha büyük bir ivme yaşayacaktır. Daha büyük kütlenin, kuvvete tepki olarak hareket durumunu değiştirmeye karşı daha büyük bir "direnç" gösterdiğini söyleyebiliriz. ⓘ

Ancak, farklı nesnelere "aynı" kuvvetleri uygulama fikri bizi kuvvetin ne olduğunu tam olarak tanımlamadığımız gerçeğine geri götürür. Bu zorluğu Newton'un üçüncü yasasının yardımıyla aşabiliriz; bu yasaya göre bir cisim ikinci bir cisme kuvvet uygularsa, ikinci cisim de ona eşit ve zıt bir kuvvete maruz kalacaktır. Kesin olmak gerekirse, m₁ ve m₂ sabit eylemsizlik kütlelerine sahip iki nesnemiz olduğunu varsayalım. Bu iki nesneyi diğer tüm fiziksel etkilerden izole ediyoruz, böylece mevcut tek kuvvet F₁₂ olarak gösterdiğimiz m2 tarafından m1'e uygulanan kuvvet ve F₂₁ olarak gösterdiğimiz m1 tarafından m2'ye uygulanan kuvvet olacaktır. Newton'un ikinci yasası şunu belirtir

${\begin{aligned}\mathbf {F_{12}} &=m_{1}\mathbf {a} _{1},\\\mathbf {F_{21}} &=m_{2}\mathbf {a} _{2},\end{aligned}}$

Burada a₁ ve a₂ sırasıyla m₁ ve m₂ 'nin ivmeleridir. Bu ivmelerin sıfır olmadığını, dolayısıyla iki nesne arasındaki kuvvetlerin de sıfır olmadığını varsayalım. Bu durum, örneğin iki nesne birbiriyle çarpışma sürecindeyse ortaya çıkar. Newton'un üçüncü yasasına göre

$\mathbf {F} _{12}=-\mathbf {F} _{21};$

ve böylece

$m_{1}=m_{2}{\frac {|\mathbf {a} _{2}|}{|\mathbf {a} _{1}|}}\!.$ ⓘ

Eğer |a₁| sıfır değilse, kesir iyi tanımlanmıştır ve bu da m₁'in eylemsiz kütlesini ölçmemizi sağlar. Bu durumda m₂ bizim "referans" nesnemizdir ve m kütlesini (diyelim ki) 1 kilogram olarak tanımlayabiliriz. Daha sonra evrendeki başka herhangi bir cismi referans cisimle çarpıştırarak ve ivmelerini ölçerek kütlesini ölçebiliriz. ⓘ

Ek olarak, kütle bir cismin p momentumunu v doğrusal hızıyla ilişkilendirir:

$\mathbf {p} =m\mathbf {v}$,

ve cismin kinetik enerjisi K hızına eşittir:

$K={\dfrac {1}{2}}m|\mathbf {v} |^{2}$. ⓘ

Mach'ın kütle tanımındaki temel zorluk, kütle ölçümünü gerçekleştirmek üzere iki kütleyi birbirine yeterince yaklaştırmak için gereken potansiyel enerjiyi (ya da bağlanma enerjisini) hesaba katmamasıdır. Bu durum en açık şekilde döteryum çekirdeğindeki protonun kütlesinin, serbest uzaydaki protonun kütlesiyle (yaklaşık %0,239 oranında daha büyüktür - bu döteryumun bağlanma enerjisinden kaynaklanmaktadır) karşılaştırılmasıyla gösterilebilir. Bu nedenle, örneğin, referans ağırlığı m₂ nötronun serbest uzaydaki kütlesi olarak alınırsa ve döteryumdaki proton ve nötron için göreli ivmeler hesaplanırsa, yukarıdaki formül döteryumdaki proton için m₁ kütlesini (%0,239 oranında) fazla tahmin eder. Mach'ın formülü en iyi ihtimalle sadece kütlelerin oranlarını elde etmek için kullanılabilir, yani m₁ / m₂ = |a₂| / |a₁| şeklinde. Henri Poincaré tarafından işaret edilen bir başka zorluk da anlık ivmenin ölçümünün imkansız olduğudur: zaman ya da mesafe ölçümünün aksine ivmeyi tek bir ölçümle ölçmenin bir yolu yoktur; ivmeyi elde etmek için birden fazla ölçüm (konum, zaman vb.) yapmak ve bir hesaplama gerçekleştirmek gerekir. Poincaré bunu Mach'ın kütle tanımındaki "aşılamaz bir kusur" olarak nitelendirmiştir. ⓘ

Atomik kütleler

Tipik olarak, nesnelerin kütlesi kilogram cinsinden ölçülür ve 2019'dan bu yana doğanın temel sabitleri cinsinden tanımlanır. Bir atomun veya başka bir parçacığın kütlesi, başka bir atomunkiyle daha kesin ve daha uygun bir şekilde karşılaştırılabilir ve bu nedenle bilim insanları daltonu (birleşik atomik kütle birimi olarak da bilinir) geliştirmiştir. Tanım olarak, 1 Da (bir dalton) bir karbon-12 atomunun kütlesinin tam olarak on ikide biridir ve dolayısıyla bir karbon-12 atomu tam olarak 12 Da kütleye sahiptir. ⓘ

Görelilikte

Özel görelilik

Özel göreliliğin bazı çerçevelerinde, fizikçiler terimin farklı tanımlarını kullanmışlardır. Bu çerçevelerde iki tür kütle tanımlanır: durgun kütle (değişmez kütle) ve rölativistik kütle (hız ile artan). Durgun kütle, nesne ile birlikte hareket eden bir gözlemci tarafından ölçülen Newton kütlesidir. Göreli kütle ise bir cisim ya da sistemdeki toplam enerji miktarının c²'ye bölünmesiyle elde edilir. Bu ikisi aşağıdaki denklemle ilişkilidir:

$m_{\mathrm {relative} }=\gamma (m_{\mathrm {rest} })\!$ ⓘ

burada $\gamma$ Lorentz faktörüdür:

$\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}$ ⓘ

Sistemlerin değişmez kütlesi tüm eylemsiz çerçevelerdeki gözlemciler için aynıyken, göreli kütle gözlemcinin referans çerçevesine bağlıdır. Fizik denklemlerini, kütle değerleri gözlemciler arasında değişmeyecek şekilde formüle etmek için, durgun kütle kullanmak uygundur. Bir cismin durgun kütlesi aynı zamanda E enerjisi ve p momentumunun büyüklüğü ile rölativistik enerji-momentum denklemi ile ilişkilidir:

$(m_{\mathrm {rest} })c^{2}={\sqrt {E_{\mathrm {total} }^{2}-(|\mathbf {p} |c)^{2}}}.\!$ ⓘ

Sistem kütle ve enerji açısından kapalı olduğu sürece, her iki kütle türü de herhangi bir referans çerçevesinde korunur. Kütlenin korunumu, bazı parçacık türleri diğerlerine dönüşse bile geçerlidir. Madde parçacıkları (atomlar gibi) madde olmayan parçacıklara (ışık fotonları gibi) dönüşebilir, ancak bu toplam kütle veya enerji miktarını etkilemez. Isı gibi şeyler madde olmasa da, her tür enerji yine de kütle sergilemeye devam eder. Dolayısıyla, görelilikte kütle ve enerji birbirine dönüşmez; aksine, her ikisi de aynı şeyin adıdır ve ne kütle ne de enerji diğeri olmadan ortaya çıkar. ⓘ

Hem durgun hem de göreli kütle, iyi bilinen E = mc² ilişkisi uygulanarak bir enerji olarak ifade edilebilir ve sırasıyla durgun enerji ve "göreli enerji" (toplam sistem enerjisi) elde edilir:

$E_{\mathrm {rest} }=(m_{\mathrm {rest} })c^{2}\!$

$E_{\mathrm {total} }=(m_{\mathrm {relative} })c^{2}\!$ ⓘ

"Rölativistik" kütle ve enerji kavramları "durgun" muadilleriyle ilişkilidir, ancak net momentumun olduğu sistemlerde durgun muadilleriyle aynı değere sahip değildirler. Rölativistik kütle enerji ile orantılı olduğundan, fizikçiler arasında giderek kullanılmaz hale gelmiştir. Kavramın pedagojik olarak yararlı olup olmadığı konusunda anlaşmazlık vardır. ⓘ

Bağlı sistemlerde, bağlanma enerjisi genellikle bağlı olmayan sistemin kütlesinden çıkarılmalıdır, çünkü bağlanma enerjisi genellikle bağlandığı anda sistemi terk eder. Sistemin kütlesi bu süreçte değişir çünkü sistem bağlanma süreci sırasında kapalı değildi, bu nedenle enerji kaçtı. Örneğin, atom çekirdeklerinin bağlanma enerjisi, çekirdekler oluşurken genellikle gama ışınları şeklinde kaybolur ve geriye, oluştukları serbest parçacıklardan (nükleonlar) daha az kütleye sahip nüklitler kalır. ⓘ

Kütle-enerji eşdeğerliği makroskopik sistemlerde de geçerlidir. Örneğin, tam olarak bir kilogram buz alınır ve ısı uygulanırsa, ortaya çıkan eriyik suyun kütlesi bir kilogramdan fazla olacaktır: buzu eritmek için kullanılan termal enerjiden (gizli ısı) gelen kütleyi de içerecektir; bu enerjinin korunumundan kaynaklanır. Bu sayı küçüktür ancak ihmal edilebilir değildir: yaklaşık 3,7 nanogram. Eriyen buzun gizli ısısının (334 kJ/kg) ışık hızının karesine (c² ≈ 9×10¹⁶ m²/s²) bölünmesiyle elde edilir. ⓘ

Genel görelilik

Genel görelilikte eşdeğerlik ilkesi, yerçekimsel ve eylemsiz kütlenin eşdeğerliğidir. Bu iddianın özünde Albert Einstein'ın, kütleli bir cisim (Dünya gibi) üzerinde dururken yerel olarak deneyimlenen yerçekimi kuvvetinin, eylemsiz (yani ivmeli) bir referans çerçevesindeki bir gözlemcinin deneyimlediği sözde kuvvetle aynı olduğu fikri yatar. ⓘ

Ancak, genel görelilikte değişmez kütle kavramı için nesnel bir genel tanım bulmanın imkansız olduğu ortaya çıkmıştır. Sorunun özünde Einstein alan denklemlerinin doğrusal olmaması yatar, bu da kütleçekim alanı enerjisini stres-enerji tensörünün bir parçası olarak tüm gözlemciler için değişmez bir şekilde yazmayı imkansız kılar. Belirli bir gözlemci için bu, stres-enerji-momentum psödotensörü ile sağlanabilir. ⓘ

Kuantum fiziğinde

Klasik mekanikte, bir parçacığın hareketsiz kütlesi Euler-Lagrange denkleminde bir m parametresi olarak görünür:

${\frac {\mathrm {d} }{\mathrm {d} t}}\ \left(\,{\frac {\partial L}{\partial {\dot {x}}_{i}}}\,\right)\ =\ m\,{\ddot {x}}_{i}$. ⓘ

Kuantizasyondan sonra, x konum vektörü bir dalga fonksiyonu ile değiştirildiğinde, m parametresi kinetik enerji operatöründe görünür:

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)=\left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} )\right)\Psi (\mathbf {r} ,\,t)$. ⓘ

Görünüşte kovaryant (göreli olarak değişmez) Dirac denkleminde ve doğal birimlerde bu şöyle olur:

$(-i\gamma ^{\mu }\partial _{\mu }+m)\psi =0\,$

Burada "kütle" parametresi m artık basitçe dalga fonksiyonu ψ tarafından tanımlanan kuantumla ilişkili bir sabittir. ⓘ

1960'larda geliştirilen parçacık fiziğinin Standart Modelinde bu terim, ψ alanının ek bir alan olan Φ, yani Higgs alanına bağlanmasından kaynaklanır. Fermiyonlar söz konusu olduğunda, Higgs mekanizması Lagrangian'daki mψ teriminin yerine $G_{\psi }{\overline {\psi }}\phi \psi$. Bu, her bir temel parçacığın kütlesine ilişkin değerin açıklamasını, bilinmeyen bağlantı sabiti G_ψ'nin değerine kaydırır. ⓘ

Takyonik parçacıklar ve hayali (karmaşık) kütle

Takyonik alan ya da kısaca takyon, hayali kütleye sahip bir kuantum alanıdır. Takyonlar (ışıktan daha hızlı hareket eden parçacıklar) genel olarak var olduğuna inanılmayan tamamen varsayımsal bir kavram olmasına rağmen, hayali kütleye sahip alanlar modern fizikte önemli bir rol oynamaya başlamış ve popüler fizik kitaplarında tartışılmıştır. Bu tür teorilerde hiçbir koşul altında hiçbir uyarım ışıktan daha hızlı yayılmaz - takyonik bir kütlenin varlığı ya da yokluğu sinyallerin maksimum hızı üzerinde hiçbir etkiye sahip değildir (nedensellik ihlali yoktur). Alan hayali kütleye sahip olsa da, herhangi bir fiziksel parçacık değildir; "hayali kütle" sistemin kararsız hale geldiğini gösterir ve mevcut parçacık fiziği modellerinde simetri kırılmasıyla sonuçlanan takyon yoğunlaşması (ikinci dereceden faz geçişleriyle yakından ilgilidir) adı verilen bir tür faz geçişinden geçerek kararsızlıktan kurtulur. ⓘ

"Takyon" terimi Gerald Feinberg tarafından 1967 tarihli bir makalede ortaya atılmıştır, ancak kısa süre sonra Feinberg'in modelinin aslında süperluminal hızlara izin vermediği anlaşılmıştır. Bunun yerine, hayali kütle konfigürasyonda bir istikrarsızlık yaratır: - bir veya daha fazla alan uyarımının takyonik olduğu herhangi bir konfigürasyon kendiliğinden bozulur ve ortaya çıkan konfigürasyon fiziksel takyon içermez. Bu süreç takyon yoğunlaşması olarak bilinir. İyi bilinen örnekler arasında parçacık fiziğindeki Higgs bozonunun yoğunlaşması ve yoğun madde fiziğindeki ferromanyetizma sayılabilir. ⓘ

Takyonik hayali kütle kavramı, hayali kütlenin klasik bir yorumu olmadığı için rahatsız edici görünse de, kütle kuantize değildir. Aksine, skaler alan kuantize olur; takyonik kuantum alanları için bile, uzaya benzer şekilde ayrılmış noktalardaki alan operatörleri hala gidip gelir (veya ters gider), böylece nedensellik korunur. Bu nedenle, bilgi hala ışıktan daha hızlı yayılmaz ve çözümler üstel olarak büyür, ancak süperlüminal olarak büyümez (nedensellik ihlali yoktur). Takyon yoğunlaşması, yerel bir sınıra ulaşmış ve safça fiziksel takyonlar üretmesi beklenebilecek bir fiziksel sistemi, fiziksel takyonların bulunmadığı alternatif bir kararlı duruma yönlendirir. Takyonik alan potansiyelin minimumuna ulaştığında, kuantları artık takyon değil, pozitif kütle karesine sahip sıradan parçacıklardır. ⓘ

Bu, kararsız kütleli parçacıkların resmi olarak karmaşık bir kütleye sahip olarak tanımlandığı genel kuralın özel bir durumudur; gerçek kısım olağan anlamda kütleleri ve hayali kısım doğal birimlerdeki bozunma oranıdır. Bununla birlikte, kuantum alan teorisinde, bir parçacık ("tek parçacık durumu") kabaca zaman içinde sabit olan bir durum olarak tanımlanır; yani Hamiltonyen'in bir özdeğeri. Kararsız bir parçacık, zaman içinde sadece yaklaşık olarak sabit olan bir durumdur; Ölçülebilecek kadar uzun süre var olursa, resmi olarak karmaşık bir kütleye sahip olarak tanımlanabilir, kütlenin gerçek kısmı hayali kısmından daha büyüktür. Her iki kısım da aynı büyüklükteyse, bu bir parçacıktan ziyade saçılma sürecinde ortaya çıkan bir rezonans olarak yorumlanır, çünkü saçılma sürecinden bağımsız olarak ölçülebilecek kadar uzun süre var olmadığı kabul edilir. Bir takyon durumunda, kütlenin gerçek kısmı sıfırdır ve dolayısıyla ona hiçbir parçacık kavramı atfedilemez. ⓘ

Lorentz değişmez teorisinde, sıradan ışıktan yavaş parçacıklar (takyon tartışmalarında bazen "bradyonlar" olarak adlandırılır) için geçerli olan formüllerin aynısı takyonlar için de geçerli olmalıdır. Özellikle enerji-momentum ilişkisi:

$E^{2}=p^{2}c^{2}+m^{2}c^{4}\;$

(burada p bradyonun rölativistik momentumu ve m de durgun kütlesidir) bir parçacığın toplam enerjisine ilişkin formülle birlikte geçerli olmalıdır:

$E={\frac {mc^{2}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.$

Bu denklem, bir parçacığın (bradyon ya da takyon) toplam enerjisinin, durgun kütlesinden ("durgun kütle enerjisi") ve hareketinden, kinetik enerjiden gelen bir katkı içerdiğini gösterir. v, c'den büyük olduğunda, radikalin altındaki değer negatif olduğundan, enerji denklemindeki payda "hayali "dir. Toplam enerjinin gerçek olması gerektiğinden, pay da hayali olmalıdır: yani, saf hayali bir sayının başka bir saf hayali sayıya bölümü gerçek bir sayı olduğundan, durgun kütle m hayali olmalıdır. ⓘ

Kütle-Hız Değişimi

Kuantum mekaniğine göre hızı artan bir cismin kütlesi de artmaktadır. Fakat bu değişim küçük hızlarda ihmal edilebilecek kadar azdır. bu değişim aşağıdaki formül ile hesaplanır:
$m={\frac {m_{0}}{\sqrt {1-(v^{2}/c^{2})}}}$
Burada $m$: Kütle değişimini, $m_{0}$: İlk kütleyi, $v$: Cismin hızını, $c$: ışık hızını temsil eder. ⓘ