Titreşim

Titreşim, bir denge noktası etrafında salınımların meydana geldiği mekanik bir olgudur. Kelime Latince vibrationem'den ("sallama, sallanma") gelmektedir. Salınımlar, bir sarkacın hareketi gibi periyodik ya da çakıllı bir yolda bir lastiğin hareketi gibi rastgele olabilir. ⓘ

Titreşim arzu edilen bir şey olabilir: örneğin bir diyapazonun hareketi, bir nefesli çalgıdaki veya mızıkadaki kamış, bir cep telefonu veya bir hoparlörün konisi. ⓘ

Ancak birçok durumda titreşim istenmeyen bir durumdur, enerjiyi boşa harcar ve istenmeyen sesler yaratır. Örneğin, motorların, elektrik motorlarının veya çalışan herhangi bir mekanik cihazın titreşim hareketleri tipik olarak istenmeyen hareketlerdir. Bu tür titreşimlere dönen parçalardaki dengesizlikler, eşit olmayan sürtünme veya dişli dişlerinin birbirine geçmesi neden olabilir. Dikkatli tasarımlar genellikle istenmeyen titreşimleri en aza indirir. ⓘ

Ses ve titreşim çalışmaları yakından ilişkilidir. Ses veya basınç dalgaları, titreşen yapılar (örneğin ses telleri) tarafından üretilir; bu basınç dalgaları aynı zamanda yapıların (örneğin kulak zarı) titreşimine de neden olabilir. Bu nedenle, gürültüyü azaltma girişimleri genellikle titreşim sorunlarıyla ilişkilidir. ⓘ

Dairesel bir tamburun olası titreşim modlarından biri (bkz. diğer modlar). ⓘ

Araba süspansiyonu: Titreşim kontrolü tasarımı akustik, otomotiv veya makine mühendisliğinin bir parçası olarak üstlenilir. ⓘ

Titreşim türleri

Serbest titreşim, mekanik bir sistem bir ilk girdi ile harekete geçirildiğinde ve serbestçe titreşmesine izin verildiğinde meydana gelir. Bu tür titreşime örnek olarak bir çocuğun salıncakta geri çekilip bırakılması veya bir diyapazon çatalına vurulup çalmasına izin verilmesi verilebilir. Mekanik sistem bir veya daha fazla doğal frekansında titreşir ve hareketsizliğe doğru sönümlenir. ⓘ

Zorlanmış titreşim, mekanik bir sisteme zamanla değişen bir rahatsızlık (yük, yer değiştirme, hız veya ivme) uygulandığında ortaya çıkar. Bozukluk periyodik ve sabit durumlu bir girdi, geçici bir girdi veya rastgele bir girdi olabilir. Periyodik giriş harmonik veya harmonik olmayan bir bozulma olabilir. Bu tür titreşimlere örnek olarak bir dengesizlik nedeniyle sallanan bir çamaşır makinesi, bir motorun veya düzensiz bir yolun neden olduğu ulaşım titreşimi veya bir deprem sırasında bir binanın titreşimi verilebilir. Doğrusal sistemler için, periyodik, harmonik bir girişin uygulanmasından kaynaklanan kararlı durum titreşim tepkisinin frekansı, uygulanan kuvvet veya hareketin frekansına eşittir ve tepki büyüklüğü gerçek mekanik sisteme bağlıdır. ⓘ

Sönümlü titreşim: Titreşen bir sistemin enerjisi sürtünme ve diğer dirençler tarafından kademeli olarak dağıtıldığında, titreşimlerin sönümlendiği söylenir. Titreşimlerin frekansı veya şiddeti kademeli olarak azalır veya değişir ya da durur ve sistem denge konumunda kalır. Bu tür titreşimlere örnek olarak amortisör tarafından sönümlenen araç süspansiyonu verilebilir. ⓘ

Titreşim testi

Titreşim testi, genellikle bir tür çalkalayıcı ile bir yapıya bir zorlama işlevi getirilerek gerçekleştirilir. Alternatif olarak, bir DUT (test edilen cihaz) bir çalkalayıcının "tablasına" bağlanır. Titreşim testi, test edilen bir cihazın (DUT) tanımlanmış bir titreşim ortamına verdiği tepkiyi incelemek için gerçekleştirilir. Ölçülen tepki, titreşim ortamında çalışma kabiliyeti, yorulma ömrü, rezonans frekansları veya gıcırtı ve çıngırak sesi çıkışı (NVH) olabilir. Gıcırtı ve çıngırak testi, çalışma sırasında çok düşük ses seviyeleri üreten özel bir sessiz çalkalayıcı türü ile gerçekleştirilir. ⓘ

Nispeten düşük frekanslı zorlamalar için (tipik olarak 100 Hz'den az) servohidrolik (elektrohidrolik) çalkalayıcılar kullanılır. Daha yüksek frekanslar için (tipik olarak 5 Hz ila 2000 Hz) elektrodinamik çalkalayıcılar kullanılır. Genel olarak, bir titreşim tertibatının DUT tarafında bulunan bir veya daha fazla "giriş" veya "kontrol" noktası belirli bir ivmede tutulur. Diğer "yanıt" noktaları, kontrol noktalarından daha yüksek titreşim seviyelerine (rezonans) veya daha düşük titreşim seviyelerine (anti-rezonans veya sönümleme) maruz kalabilir. Bir sistemin çok gürültülü olmasını önlemek veya belirli titreşim frekanslarının neden olduğu titreşim modları nedeniyle belirli parçalar üzerindeki gerilimi azaltmak için genellikle anti-rezonans elde etmek istenir. ⓘ

Titreşim testi laboratuvarları tarafından yürütülen en yaygın titreşim testi hizmetleri sinüzoidal ve rastgele titreşim testleridir. Sinüs (her seferinde bir frekans) testleri, test edilen cihazın (DUT) yapısal tepkisini incelemek için gerçekleştirilir. Titreşim testinin erken tarihi boyunca, titreşim makinesi kontrolörleri sadece sinüs hareketini kontrol etmekle sınırlıydı, bu nedenle sadece sinüs testi yapıldı. Daha sonra, daha sofistike analog ve ardından dijital kontrolörler rastgele kontrol (aynı anda tüm frekanslar) sağlayabilmiştir. Rastgele (tüm frekanslar aynı anda) bir testin genellikle hareket halindeki bir otomobilin yol girdileri gibi gerçek dünya ortamını daha yakından taklit ettiği kabul edilir. ⓘ

Çoğu titreşim testi, gerçek dünyadaki titreşimlerin çoğu aynı anda çeşitli eksenlerde meydana gelmesine rağmen, bir seferde 'tek bir DUT ekseninde' gerçekleştirilir. 2008'in sonlarında yayınlanan MIL-STD-810G, Test Yöntemi 527, çoklu uyarıcı testi gerektirir. DUT'yi çalkalayıcı tablaya bağlamak için kullanılan titreşim testi fikstürü, titreşim testi spektrumunun frekans aralığı için tasarlanmalıdır. Gerçek kullanımdaki montajın dinamik tepkisini (mekanik empedans) kopyalayan bir titreşim testi fikstürü tasarlamak zordur. Bu nedenle, titreşim testleri arasında tekrarlanabilirliği sağlamak için, titreşim fikstürleri test frekansı aralığında rezonanssız olacak şekilde tasarlanır. Genel olarak daha küçük armatürler ve daha düşük frekans aralıkları için tasarımcı, test frekansı aralığında rezonans içermeyen bir armatür tasarımını hedefleyebilir. DUT büyüdükçe ve test frekansı arttıkça bu daha zor hale gelir. Bu durumlarda çok noktalı kontrol stratejileri, gelecekte mevcut olabilecek bazı rezonansları azaltabilir. ⓘ

Bazı titreşim testi yöntemleri, titreşim testi fikstürü tarafından sergilenmesine izin verilen çapraz karışma (bir yanıt noktasının test edilen eksene karşılıklı olarak dik bir yönde hareket etmesi) miktarını sınırlar. Titreşimleri izlemek veya kaydetmek için özel olarak tasarlanmış cihazlara vibroskop denir. ⓘ

Titreşim analizi

Endüstriyel veya bakım ortamında uygulanan titreşim analizi (VA), ekipman arızalarını tespit ederek bakım maliyetlerini ve ekipman arıza süresini azaltmayı amaçlar. VA, durum izleme (CM) programının önemli bir bileşenidir ve genellikle kestirimci bakım (PdM) olarak adlandırılır. En yaygın olarak VA, dönen ekipmanlarda (Fanlar, Motorlar, Pompalar ve Dişli Kutuları vb.) dengesizlik, yanlış hizalama, yuvarlanma elemanı yatak arızaları ve rezonans koşulları gibi arızaları tespit etmek için kullanılır. ⓘ

VA, zaman dalga formu (TWF) olarak görüntülenen Deplasman, Hız ve İvme birimlerini kullanabilir, ancak en yaygın olarak TWF'nin hızlı Fourier dönüşümünden türetilen spektrum kullanılır. Titreşim spektrumu, arızalı bileşeni tam olarak belirleyebilecek önemli frekans bilgileri sağlar. ⓘ

Titreşim analizinin temelleri, basit Kütle-yay-sönümleyici modeli incelenerek anlaşılabilir. Aslında, otomobil gövdesi gibi karmaşık bir yapı bile basit kütle-yay-sönümleyici modellerinin bir "toplamı" olarak modellenebilir. Kütle-yay-sönümleyici modeli basit bir harmonik osilatör örneğidir. Davranışını tanımlamak için kullanılan matematik, RLC devresi gibi diğer basit harmonik osilatörlerle aynıdır. ⓘ

Not: Bu makale adım adım matematiksel türetmeleri içermez, ancak temel titreşim analizi denklemlerine ve kavramlarına odaklanır. Ayrıntılı türetmeler için lütfen makalenin sonundaki referanslara başvurun. ⓘ

Sönümleme olmadan serbest titreşim

Basit kütle yay modeli

Kütle-yay-sönümleyici incelemesine başlamak için sönümlemenin ihmal edilebilir olduğunu ve kütleye uygulanan herhangi bir dış kuvvet olmadığını (yani serbest titreşim) varsayalım. Yay tarafından kütleye uygulanan kuvvet, yayın gerildiği "x" miktarı ile orantılıdır (yayın kütlenin ağırlığı nedeniyle zaten sıkıştırılmış olduğu varsayılır). Orantı sabiti, k, yayın sertliğidir ve kuvvet/mesafe birimlerine sahiptir (örn. lbf/in veya N/m). Negatif işaret, kuvvetin her zaman kendisine bağlı kütlenin hareketine karşı olduğunu gösterir:

$F_{s}=-kx.\!$

Kütle tarafından üretilen kuvvet, Newton'un ikinci hareket yasası tarafından verildiği gibi kütlenin ivmesi ile orantılıdır:

$\Sigma \ F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}.$

Kütle üzerindeki kuvvetlerin toplamı bu adi diferansiyel denklemi oluşturur: $\ m{\ddot {x}}+kx=0.$

Kütle-yay sisteminin basit harmonik hareketi

Titreşimin başlamasının, yayın A mesafesi kadar gerilmesi ve serbest bırakılmasıyla başladığını varsayarsak, kütlenin hareketini tanımlayan yukarıdaki denklemin çözümü şudur:

$x(t)=A\cos(2\pi f_{n}t).\!$

Bu çözüm, A genliğine ve fn frekansına sahip basit harmonik hareketle salınacağını söyler. fn sayısına sönümlenmemiş doğal frekans denir. Basit kütle-yay sistemi için fn şu şekilde tanımlanır:

$f_{n}={1 \over {2\pi }}{\sqrt {k \over m}}.\!$ ⓘ

Not: Saniyede radyan birimine sahip açısal frekans ω (ω=2 π f) denklemlerde sıklıkla kullanılır çünkü denklemleri basitleştirir, ancak normalde bir sistemin frekansını belirtirken normal frekansa (Hz birimleri veya eşdeğer olarak saniyede devir) dönüştürülür. Sistemin kütlesi ve sertliği biliniyorsa, yukarıdaki formül, başlangıçtaki bir rahatsızlık tarafından harekete geçirildiğinde sistemin titreştiği frekansı belirleyebilir. Titreşen her sistemin, rahatsız edildiğinde titreştiği bir veya daha fazla doğal frekansı vardır. Bu basit ilişki, kütle veya sertlik eklediğimizde daha karmaşık bir sisteme ne olduğunu genel olarak anlamak için kullanılabilir. Örneğin, yukarıdaki formül, bir araba veya kamyon tamamen yüklendiğinde, süspansiyonun neden yüksüz halinden ″daha yumuşak″ hissettiğini açıklar - kütle artmış ve sistemin doğal frekansını azaltmıştır. ⓘ

Kütle üzerindeki kuvvetleri toplayıp aşağıdaki adi diferansiyel denkleme ulaşırız:

$m{\ddot {x}}+kx=0.$ ⓘ

Bu çözüm şu anlamdadır: kütle “A” genliğinde ve $f_{n}$ frekansında salınmaktadır, burada $f_{n}$ titreşim analizindeki en önemli değerlerden biridir ve sönümsüz “doğal frekans” olarak adlandırılır. ⓘ

Sistemin titreşmesine neden olan şey: enerjinin korunumu bakış açısından

Titreşimsel hareket enerjinin korunumu açısından anlaşılabilir. Yukarıdaki örnekte yay bir x değeri kadar uzatılmıştır ve bu nedenle bir miktar potansiyel enerji (${\tfrac {1}{2}}kx^{2}$) yayda depolanır. Yay serbest bırakıldığında gerilmemiş durumuna (minimum potansiyel enerji durumu) dönme eğilimindedir ve bu süreçte kütleyi hızlandırır. Yayın gerilmemiş durumuna ulaştığı noktada, onu gererek sağladığımız tüm potansiyel enerji kinetik enerjiye dönüşmüştür (${\tfrac {1}{2}}mv^{2}$). Kütle daha sonra yavaşlamaya başlar çünkü artık yayı sıkıştırmakta ve bu süreçte kinetik enerjiyi potansiyeline geri aktarmaktadır. Böylece yayın salınımı, kinetik enerjinin potansiyel enerjiye ileri geri aktarılması anlamına gelir. Bu basit modelde kütle sonsuza kadar aynı büyüklükte salınmaya devam eder - ancak gerçek bir sistemde, sönümleme her zaman enerjiyi dağıtır ve sonunda yayı dinlenmeye getirir. ⓘ

Sönümlü serbest titreşim

Kütle-yay-sönümleyici modeli ⓘ

Modele bir "viskoz" sönümleyici eklendiğinde, bu kütlenin hızıyla orantılı bir kuvvet ortaya çıkarır. Sönümleme viskoz olarak adlandırılır çünkü bir nesne içindeki bir sıvının etkilerini modeller. Orantı sabiti c, sönümleme katsayısı olarak adlandırılır ve hız üzerinden Kuvvet (lbf⋅s/in veya N⋅s/m) birimlerine sahiptir. ⓘ

$F_{\text{d}}=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}.$ ⓘ

Kütle üzerindeki kuvvetlerin toplanması aşağıdaki adi diferansiyel denklemle sonuçlanır:

$m{\ddot {x}}+c{\dot {x}}+kx=0.$ ⓘ

Bu denklemin çözümü sönümleme miktarına bağlıdır. Sönümleme yeterince küçükse, sistem hala titreşir - ancak sonunda, zamanla, titreşmeyi durdurur. Bu durum, titreşim analizinde önemli olan yetersiz sönümleme olarak adlandırılır. Sönümleme, sistemin artık salınım yapmadığı noktaya kadar artırılırsa, sistem kritik sönümleme noktasına ulaşmıştır. Sönümleme kritik sönümlemeyi geçecek şekilde artırılırsa sistem aşırı sönümlenmiş olur. Kütle-yay-sönümleyici modelinde kritik sönümleme için sönümleme katsayısının ulaşması gereken değer:

$c_{\text{c}}=2{\sqrt {\text{km}}}.$ ⓘ

Bir sistemdeki sönümleme miktarını karakterize etmek için sönümleme oranı (sönümleme faktörü ve % kritik sönümleme olarak da bilinir) adı verilen bir oran kullanılır. Bu sönümleme oranı, gerçek sönümlemenin kritik sönümlemeye ulaşmak için gereken sönümleme miktarına oranıdır. Sönümleme oranının formülü ($\zeta$) kütle-yay-sönümleyici modelidir:

$\zeta ={c \over 2{\sqrt {\text{km}}}}.$ ⓘ

Örneğin, metal yapılar (örneğin, uçak gövdeleri, motor krank milleri) 0,05'ten daha düşük sönümleme faktörlerine sahipken, otomotiv süspansiyonları 0,2-0,3 aralığındadır. Kütle-yay-sönümleyici modeli için az sönümlü sistemin çözümü aşağıdaki gibidir:

$x(t)=Xe^{-\zeta \omega _{n}t}\cos \left({\sqrt {1-\zeta ^{2}}}\omega _{n}t-\phi \right),\qquad \omega _{n}=2\pi f_{n}.$ ⓘ

0,1 ve 0,3 sönümleme oranı ile serbest titreşim ⓘ

X'in değeri, başlangıç büyüklüğü ve $\phi ,$ faz kayması, yayın gerildiği miktara göre belirlenir. Bu değerler için formüller referanslarda bulunabilir. ⓘ

Sönümlü ve sönümsüz doğal frekanslar

Şimdi sisteme kütlenin hızıyla orantılı olarak kuvvet üreten viskoz bir sönümleyici ekliyoruz.Sönümleme viskoz olarak adlandırılmaktadır çünkü bir akışkanın içindeki bir objeyi modellemektedir. Orantı sabiti “c” sönüm katsayısı olarak adlandırılır ve kuvvet/hız birimindedir(lbf s/ in veya N s/m). ⓘ

$F_{d}=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}\!$ ⓘ

Kütle üzerindeki kuvvetleri toplayarak aşağıdaki adi diferansiyel denlemi elde ederiz:

$m{\ddot {x}}+{c}{\dot {x}}+{k}x=0.$ ⓘ

Bu denklemin çözümü sönümün miktarına bağlıdır. Eğer sönüm yeterince küçükse sistem titreşecek fakat zaman geçtikçe titremesi sona erecektir. Bu durumda sistem az sönümlü olarak ifade edilir—titreşim analizinin en çok ilgi çeken kısmıdır. Eğer sönümü sistemin artık salınmadığı noktaya kadar arttırırsak kritik sönüme ulaşmış oluruz(eğer sönümü kritik sönümün üzerine de çıkarırsak sistem aşırı sönümlü sistem olarak adlandırılır). Kütle yay sönüm modelinde kritik sönüm için sönüm katsayısının ulaşması gereken değer şudur:

$c_{c}=2{\sqrt {km}}$ ⓘ

Sistemdeki sönümü tanımlamak için sönüm oranı(sönüm faktörü ve % kritik sönüm de denir) denen bir oran kullanılır. Bu oran sistemdeki gerçek sönümün, kritik sönüme ulaşması için gereken sönüme oranıdır.Kütle yay sönüm modeli için sönüm oranı ($\zeta$) formülü ise şöyledir:

$\zeta ={c \over 2{\sqrt {km}}}.$ ⓘ

Örneğin; metal yapılar(uçak gövdeleri, motor krank milleri gibi) 0.05 den daha küçük sönümleme faktörlerine sahipken, otomotiv süspansiyonları 0.2-0.3 aralığındadır. ⓘ

Az sönümlü kütle yay sönüm sistemi için çözüm aşağıdaki gibidir:

$x(t)=Xe^{-\zeta \omega _{n}t}\cos({{\sqrt {1-\zeta ^{2}}}\omega _{n}t-\phi }),\ \ \omega _{n}=2\pi f_{n}$ ⓘ

Başlangıç genliği “X” ve faz farkı $\phi$ yayın ne kadar sıkıştırıldığına göre değişir. Bu değerlerin formülleri referanslarda bulunabilir. ⓘ

Bu çözümde fark edilmesi gereken önemli nokta eksponansiyel terim ve kosinüs fonksiyonudur. Eksponansiyel terim sis temin ne kadar hızlı sönümleceğini belirleyen terimdir-sönüm oranı büyüdükçe sistem daha hızlı sönümlenir. Koisinüs fonksiyonu ise çözümün salınım yapan kısmıdır ve salınımın frekansı sönümsüz durumdan farklıdır. ⓘ

Bu durumdaki frekansa sönümlü doğal frekans, $f_{d}$, denir ve aşağıdaki formüle göre sönümsüz doğal frekansla ilişkilidir:

$f_{d}={\sqrt {1-\zeta ^{2}}}f_{n}$ ⓘ

Sönümlü doğal frekans sönümsüz doğal frekanstan daha düşüktür, fakat birçok pratik durumda sönüm oranı göreceli olarak küçüktür ve bu yüzden aradaki fark göz ardı edilebilir. Bu yüzden sönümlü ve sönümsüz tanımlamalar, doğal frekanstan bahsedildiğinde, büyütülmüş olur. (Örneğin: 0.1 lik sönüm oranında; sönümlü doğal frekans sönümsüz doğal frekanstan %1 küçüktür.) ⓘ

Yandaki çizimler 0.1 ve 0.3 lük sönüm oranlarının zaman geçtikçe sistemin sönümlenmesini nasıl etkilediğini gösterir. Pratikte sıklıkla yapılan ise bir darbeden sonra (örneğin; bir çekiçle vurduktan sonra) deneysel olarak serbest titreşimi ölçmektir ve bundan sonra salınım oranını ölçerek sistemin doğal frekansı hesaplanır ve düşüş oranı ölçülerek sönüm oranı bulunur. Doğal frekans ve sönüm oranı sadece serbest titreşimde önemli değildir. Aynı zamanda sistemin zorlama altındaki titreşiminde nasıl davranacağını da belirlerler. ⓘ

Sönümleme ile zorlanmış titreşim

Yay kütleli damper modelinin davranışı harmonik bir kuvvetin eklenmesiyle değişir. Bu tür bir kuvvet, örneğin, dönen bir dengesizlik tarafından üretilebilir. ⓘ

$F=F_{0}\sin(2\pi ft).\!$ ⓘ

Kütle üzerindeki kuvvetlerin toplanması aşağıdaki adi diferansiyel denklemle sonuçlanır:

$m{\ddot {x}}+c{\dot {x}}+kx=F_{0}\sin(2\pi ft).$ ⓘ

Bu problemin kararlı durum çözümü şu şekilde yazılabilir:

$x(t)=X\sin(2\pi ft+\phi ).\!$ ⓘ

Sonuç, kütlenin uygulanan kuvvetle aynı frekansta, f, ancak faz kaymasıyla salınacağını belirtir $\phi .$ ⓘ

Titreşimin genliği "X" aşağıdaki formül ile tanımlanır. ⓘ

$X={F_{0} \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}.$ ⓘ

Burada "r", harmonik kuvvet frekansının kütle-yay-sönümleyici modelinin sönümlenmemiş doğal frekansına oranı olarak tanımlanır. ⓘ

$r={\frac {f}{f_{n}}}.$ ⓘ

Faz kayması, $\phi ,$ aşağıdaki formül ile tanımlanır. ⓘ

$\phi =\arctan \left({\frac {-2\zeta r}{1-r^{2}}}\right).$ ⓘ

"Sistemin frekans tepkisi" olarak adlandırılan bu fonksiyonların grafiği, zorlanmış titreşimdeki en önemli özelliklerden birini sunar. Hafif sönümlü bir sistemde zorlama frekansı doğal frekansa yaklaştığında ($r\approx 1$) titreşimin genliği son derece yüksek olabilir. Bu olaya rezonans adı verilir (daha sonra bir sistemin doğal frekansı genellikle rezonans frekansı olarak adlandırılır). Rotor yatak sistemlerinde, rezonans frekansını uyaran herhangi bir dönme hızı kritik hız olarak adlandırılır. ⓘ

Mekanik bir sistemde rezonans meydana gelirse bu çok zararlı olabilir ve sistemin nihai olarak arızalanmasına yol açabilir. Sonuç olarak, titreşim analizinin en önemli nedenlerinden biri, bu tür bir rezonansın ne zaman meydana gelebileceğini tahmin etmek ve ardından meydana gelmesini önlemek için hangi adımların atılacağını belirlemektir. Genlik grafiğinin gösterdiği gibi, sönümleme eklemek titreşimin büyüklüğünü önemli ölçüde azaltabilir. Ayrıca, sistemin sertliği veya kütlesi değiştirilerek doğal frekans zorlama frekansından uzaklaştırılabilirse büyüklük azaltılabilir. Sistem değiştirilemiyorsa, belki zorlama frekansı kaydırılabilir (örneğin, kuvveti üreten makinenin hızının değiştirilmesi). ⓘ

Aşağıda, frekans yanıtı grafiklerinde gösterilen zorlanmış titreşimle ilgili diğer bazı noktalar yer almaktadır. ⓘ

• Belirli bir frekans oranında, titreşimin genliği, X, kuvvetin genliği ile doğru orantılıdır $F_{0}$ (örneğin, kuvveti iki katına çıkarırsanız, titreşim de iki katına çıkar)
• Sönümleme çok az olduğunda veya hiç olmadığında, frekans oranı r < 1 olduğunda titreşim zorlama frekansı ile aynı fazda, frekans oranı r > 1 olduğunda ise 180 derece faz dışındadır
• r ≪ 1 olduğunda genlik sadece statik kuvvet altındaki yayın sapmasıdır $F_{0}.$ Bu sapma statik sapma olarak adlandırılır $\delta _{st}.$ Dolayısıyla, r ≪ 1 olduğunda damper ve kütlenin etkileri minimumdur.
• r ≫ 1 olduğunda titreşimin genliği aslında statik sapmadan daha azdır $\delta _{st}.$ Bu bölgede kütlenin oluşturduğu kuvvet (F=ma) baskındır çünkü kütlenin gördüğü ivme frekansla birlikte artar. Yayda görülen sapma, X, bu bölgede azaldığından, yayın (F = kx) tabana ilettiği kuvvet azalır. Bu nedenle, kütle-yay-sönümleyici sistemi harmonik kuvveti montaj tabanından izole eder - buna titreşim izolasyonu denir. Daha fazla sönümleme aslında r ≫ 1 olduğunda titreşim izolasyonunun etkilerini azaltır çünkü sönümleme kuvveti (F = cv) de tabana iletilir.
• Sönümleme ne olursa olsun, frekans oranı r = 1 olduğunda titreşim zorlama frekansı ile 90 derece faz dışıdır, bu da sistemin doğal frekansını belirleme konusunda çok yardımcı olur.
• Sönümleme ne olursa olsun, r ≫ 1 olduğunda, titreşim zorlama frekansı ile 180 derece faz dışıdır
• Sönümleme ne olursa olsun, r ≪ 1 olduğunda, titreşim zorlama frekansı ile aynı fazdadır ⓘ

Rezonans nedenleri

Yay ve kütle enerji depolama elemanları olarak görülürse rezonansı anlamak kolaydır - kütle kinetik enerji depolarken yay potansiyel enerji depolar. Daha önce tartışıldığı gibi, kütle ve yay üzerlerinde herhangi bir dış kuvvet olmadığında, enerjiyi doğal frekansa eşit bir oranda ileri geri aktarırlar. Başka bir deyişle, hem kütleye hem de yaya verimli bir şekilde enerji pompalamak için enerji kaynağının enerjiyi doğal frekansa eşit bir hızda beslemesi gerekir. Kütleye ve yaya kuvvet uygulamak salıncaktaki bir çocuğu itmeye benzer, salıncağın daha da yükselmesini sağlamak için doğru anda bir itme gereklidir. Salıncak örneğinde olduğu gibi, büyük hareketler elde etmek için uygulanan kuvvetin yüksek olması gerekmez, sadece sisteme enerji eklemelidir. ⓘ

Damper, enerji depolamak yerine enerjiyi dağıtır. Sönümleme kuvveti hız ile orantılı olduğundan, hareket ne kadar fazla olursa, damper enerjiyi o kadar fazla dağıtır. Bu nedenle, damper tarafından dağıtılan enerjinin kuvvet tarafından eklenen enerjiye eşit olduğu bir nokta vardır. Bu noktada sistem maksimum genliğine ulaşmıştır ve uygulanan kuvvet aynı kaldığı sürece bu seviyede titreşmeye devam edecektir. Sönümleme yoksa, enerjiyi dağıtacak hiçbir şey yoktur ve teorik olarak hareket sonsuza kadar büyümeye devam edecektir. ⓘ

Kütle-yay-sönümleyici modeline "karmaşık" kuvvetlerin uygulanması

Bir önceki bölümde modele sadece basit bir harmonik kuvvet uygulanmıştı, ancak bu iki güçlü matematiksel araç kullanılarak önemli ölçüde genişletilebilir. Bunlardan ilki, bir sinyali zamanın (zaman alanı) bir fonksiyonu olarak alan ve frekansın (frekans alanı) bir fonksiyonu olarak harmonik bileşenlerine ayıran Fourier dönüşümüdür. Örneğin, kütle-yay-sönümleyici modeline aşağıdaki döngüyü tekrarlayan bir kuvvet uygulayarak - 0,5 saniye boyunca 1 newtona eşit bir kuvvet ve ardından 0,5 saniye boyunca kuvvet yok. Bu tür bir kuvvet 1 Hz kare dalga şeklindedir. ⓘ

1 Hz kare dalganın sinüs dalgalarının (harmonikler) toplamı olarak nasıl gösterilebileceği ve buna karşılık gelen frekans spektrumu. Animasyon için tıklayın ve tam çözünürlüğe gidin ⓘ

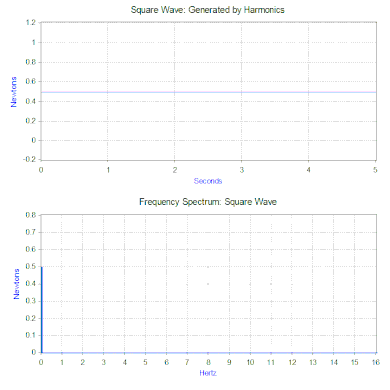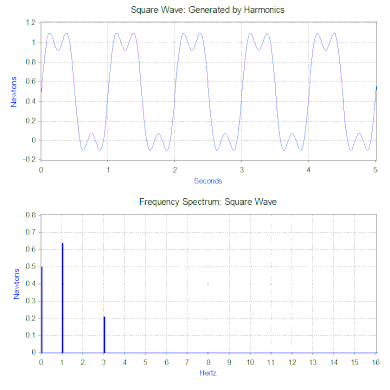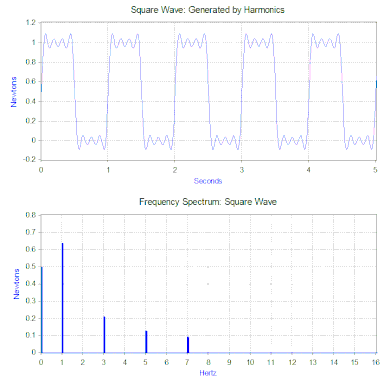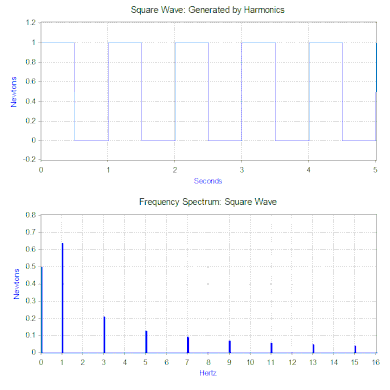
Kare dalganın Fourier dönüşümü, kare dalgayı oluşturan harmoniklerin büyüklüğünü gösteren bir frekans spektrumu üretir (faz da üretilir, ancak tipik olarak daha az endişe vericidir ve bu nedenle genellikle çizilmez). Fourier dönüşümü, geçici olaylar (örneğin darbeler) ve rastgele fonksiyonlar gibi periyodik olmayan fonksiyonları analiz etmek için de kullanılabilir. Fourier dönüşümü neredeyse her zaman bir pencere fonksiyonu ile birlikte hızlı Fourier dönüşümü (FFT) bilgisayar algoritması kullanılarak hesaplanır. ⓘ

Kare dalga kuvvetimiz söz konusu olduğunda, ilk bileşen aslında 0,5 newtonluk sabit bir kuvvettir ve frekans spektrumunda 0 Hz'de bir değerle temsil edilir. Bir sonraki bileşen 0,64 genliğe sahip 1 Hz sinüs dalgasıdır. Bu, 1 Hz'deki çizgi ile gösterilir. Kalan bileşenler tek frekanslardadır ve mükemmel kare dalgayı oluşturmak için sonsuz sayıda sinüs dalgası gerekir. Dolayısıyla Fourier dönüşümü, kuvveti daha "karmaşık" bir kuvvet (örneğin kare dalga) yerine uygulanan sinüzoidal kuvvetlerin bir toplamı olarak yorumlamanıza olanak tanır. ⓘ

Önceki bölümde titreşim çözümü tek bir harmonik kuvvet için verilmişti, ancak Fourier dönüşümü genel olarak birden fazla harmonik kuvvet verir. İkinci matematiksel araç olan süperpozisyon prensibi, sistem doğrusal ise birden fazla kuvvetin çözümlerinin toplanmasına izin verir. Yay-kütle-sönümleyici modeli durumunda, yay kuvveti yer değiştirmeyle orantılıysa ve sönümleme ilgilenilen hareket aralığı boyunca hızla orantılıysa sistem doğrusaldır. Dolayısıyla, kare dalga ile ilgili sorunun çözümü, kare dalganın frekans spektrumunda bulunan harmonik kuvvetlerin her birinden tahmin edilen titreşimin toplanmasıdır. ⓘ

Frekans tepki modeli

Bir titreşim probleminin çözümü, kuvvetin girdi ve çıktının titreşim olduğu bir girdi/çıktı ilişkisi olarak görülebilir. Kuvvet ve titreşimi frekans alanında (büyüklük ve faz) temsil etmek aşağıdaki ilişkiyi sağlar:

$X(i\omega )=H(i\omega )\cdot F(i\omega ){\text{ or }}H(i\omega )={X(i\omega ) \over F(i\omega )}.$ ⓘ

$H(i\omega )$ Frekans tepki fonksiyonu olarak adlandırılır (transfer fonksiyonu olarak da adlandırılır, ancak teknik olarak bu kadar doğru değildir) ve hem büyüklük hem de faz bileşenine sahiptir (karmaşık bir sayı olarak temsil edilirse, gerçek ve hayali bir bileşen). Frekans tepki fonksiyonunun (FRF) büyüklüğü daha önce kütle-yay-sönümleyici sistemi için sunulmuştu. ⓘ

$|H(i\omega )|=\left|{X(i\omega ) \over F(i\omega )}\right|={1 \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}},{\text{ where }}r={\frac {f}{f_{n}}}={\frac {\omega }{\omega _{n}}}.$ ⓘ

FRF'nin fazı da daha önce sunulmuştu:

$\angle H(i\omega )=-\arctan \left({\frac {2\zeta r}{1-r^{2}}}\right).$ ⓘ

Frekans tepki modeli ⓘ

Örneğin, kütlesi 1 kg, yay sertliği 1,93 N/mm ve sönümleme oranı 0,1 olan bir kütle-yay-sönümleyici sistemi için FRF'nin hesaplanması. Yay ve kütle değerleri bu özel sistem için 7 Hz'lik bir doğal frekans vermektedir. Daha önceki 1 Hz kare dalganın uygulanması kütlenin öngörülen titreşiminin hesaplanmasını sağlar. Şekilde ortaya çıkan titreşim gösterilmektedir. Bu örnekte kare dalganın dördüncü harmoniği 7 Hz'e denk gelmektedir. Bu nedenle kütle-yay-sönümleyicinin frekans tepkisi, giriş kuvveti nispeten düşük bir 7 Hz harmoniğe sahip olmasına rağmen yüksek bir 7 Hz titreşim verir. Bu örnek, ortaya çıkan titreşimin hem zorlama fonksiyonuna hem de kuvvetin uygulandığı sisteme bağlı olduğunu vurgulamaktadır. ⓘ

Şekilde ayrıca ortaya çıkan titreşimin zaman alanı gösterimi de gösterilmektedir. Bu, frekans alanı verilerini zaman alanına dönüştüren bir ters Fourier Dönüşümü gerçekleştirilerek yapılır. Pratikte bu nadiren yapılır çünkü frekans spektrumu gerekli tüm bilgileri sağlar. ⓘ

Frekans tepki fonksiyonunun (FRF) sistemin kütle, sönümleme ve sertlik bilgisinden hesaplanması gerekmez, ancak deneysel olarak ölçülebilir. Örneğin, bir frekans aralığında bilinen bir kuvvet uygulanırsa ve ilgili titreşimler ölçülürse, frekans tepki fonksiyonu hesaplanabilir ve böylece sistem karakterize edilebilir. Bu teknik, bir yapının titreşim özelliklerini belirlemek için deneysel modal analiz alanında kullanılır. ⓘ

Çoklu serbestlik dereceli sistemler ve mod şekilleri

İki serbestlik dereceli model ⓘ

Basit kütle-yay-sönümleyici modeli titreşim analizinin temelini oluşturur, peki ya daha karmaşık sistemler? Yukarıda açıklanan kütle-yay-sönümleyici modeline tek serbestlik dereceli (SDOF) model denir çünkü kütlenin sadece yukarı ve aşağı hareket ettiği varsayılır. Daha karmaşık sistemlerde, sistemin birden fazla yönde hareket eden daha fazla kütleye ayrıştırılması ve serbestlik derecelerinin eklenmesi gerekir. Çoklu serbestlik derecesinin (MDOF) temel kavramları, şekilde gösterildiği gibi sadece 2 serbestlik dereceli bir modele bakılarak anlaşılabilir. ⓘ

2DOF sistemin hareket denklemleri şu şekilde bulunur:

$m_{1}{\ddot {x_{1}}}+(c_{1}+c_{2}){\dot {x_{1}}}-c_{2}{\dot {x_{2}}}+(k_{1}+k_{2})x_{1}-k_{2}x_{2}=f_{1},$ ⓘ

$m_{2}{\ddot {x_{2}}}-c_{2}{\dot {x_{1}}}+(c_{2}+c_{3}){\dot {x_{2}}}-k_{2}x_{1}+(k_{2}+k_{3})x_{2}=f_{2}.\!$ ⓘ

Bu, matris formatında yeniden yazılabilir:

${\begin{bmatrix}m_{1}&0\\0&m_{2}\end{bmatrix}}{\begin{Bmatrix}{\ddot {x_{1}}}\\{\ddot {x_{2}}}\end{Bmatrix}}+{\begin{bmatrix}c_{1}+c_{2}&-c_{2}\\-c_{2}&c_{2}+c_{3}\end{bmatrix}}{\begin{Bmatrix}{\dot {x_{1}}}\\{\dot {x_{2}}}\end{Bmatrix}}+{\begin{bmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}+k_{3}\end{bmatrix}}{\begin{Bmatrix}x_{1}\\x_{2}\end{Bmatrix}}={\begin{Bmatrix}f_{1}\\f_{2}\end{Bmatrix}}.$ ⓘ

Bu matris denkleminin daha kompakt bir biçimi şu şekilde yazılabilir:

${\begin{bmatrix}M\end{bmatrix}}{\begin{Bmatrix}{\ddot {x}}\end{Bmatrix}}+{\begin{bmatrix}C\end{bmatrix}}{\begin{Bmatrix}{\dot {x}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{Bmatrix}x\end{Bmatrix}}={\begin{Bmatrix}f\end{Bmatrix}}$ ⓘ

burada ${\begin{bmatrix}M\end{bmatrix}},$ ${\begin{bmatrix}C\end{bmatrix}},$ ve ${\begin{bmatrix}K\end{bmatrix}}$ sırasıyla kütle, sönümleme ve sertlik matrisleri olarak adlandırılan simetrik matrislerdir. Bu matrisler NxN kare matrislerdir ve burada N sistemin serbestlik derecesi sayısıdır. ⓘ

Aşağıdaki analiz, sönümlemenin ve uygulanan kuvvetlerin olmadığı (yani serbest titreşim) durumu içermektedir. Viskoz olarak sönümlenmiş bir sistemin çözümü biraz daha karmaşıktır. ⓘ

${\begin{bmatrix}M\end{bmatrix}}{\begin{Bmatrix}{\ddot {x}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{Bmatrix}x\end{Bmatrix}}=0.$ ⓘ

Bu diferansiyel denklem aşağıdaki türde bir çözüm varsayılarak çözülebilir:

${\begin{Bmatrix}x\end{Bmatrix}}={\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}.$ ⓘ

Not: Üstel çözümü kullanarak ${\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}$ doğrusal diferansiyel denklemleri çözmek için kullanılan matematiksel bir hiledir. Euler'in formülünü kullanarak ve çözümün sadece reel kısmını alarak 1 DOF sistemi için aynı kosinüs çözümü elde edilir. Üstel çözüm sadece matematiksel olarak manipüle edilmesi daha kolay olduğu için kullanılır. ⓘ

Bu durumda denklem şöyle olur:

${\begin{bmatrix}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}=0.$ ⓘ

Beri $e^{i\omega t}$ sıfıra eşit olamaz, denklem aşağıdakine indirgenir. ⓘ

${\begin{bmatrix}{\begin{bmatrix}K\end{bmatrix}}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0.$ ⓘ

Özdeğer problemi

Bu, matematikte bir özdeğer problemi olarak adlandırılır ve denklemin şu şekilde önceden çarpılmasıyla standart formata sokulabilir ${\begin{bmatrix}M\end{bmatrix}}^{-1}$ ⓘ

${\begin{bmatrix}{\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}K\end{bmatrix}}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}M\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0$ ⓘ

ve eğer: ${\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}K\end{bmatrix}}={\begin{bmatrix}A\end{bmatrix}}$ ve $\lambda =\omega ^{2}\,$ ⓘ

${\begin{bmatrix}{\begin{bmatrix}A\end{bmatrix}}-\lambda {\begin{bmatrix}I\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0.$ ⓘ

Problemin çözümü N özdeğer ile sonuçlanır (yani $\omega _{1}^{2},\omega _{2}^{2},\cdots \omega _{N}^{2}$) ile sonuçlanır; burada N serbestlik derecesi sayısına karşılık gelir. Özdeğerler sistemin doğal frekanslarını verir. Bu özdeğerler orijinal denklem setinde tekrar yerine konulduğunda ${\begin{Bmatrix}X\end{Bmatrix}}$ her bir özdeğere karşılık gelen özvektörler olarak adlandırılır. Bu özvektörler sistemin mod şekillerini temsil eder. Bir özdeğer probleminin çözümü oldukça zahmetli olabilir (özellikle çok sayıda serbestlik derecesine sahip problemler için), ancak neyse ki çoğu matematik analiz programının özdeğer rutinleri vardır. ⓘ

Özdeğerler ve özvektörler genellikle aşağıdaki matris formatında yazılır ve sistemin modal modelini tanımlar:

${\begin{bmatrix}^{\diagdown }\omega _{r\diagdown }^{2}\end{bmatrix}}={\begin{bmatrix}\omega _{1}^{2}&\cdots &0\\\vdots &\ddots &\vdots \\0&\cdots &\omega _{N}^{2}\end{bmatrix}}{\text{ and }}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}\psi _{1}\end{Bmatrix}}{\begin{Bmatrix}\psi _{2}\end{Bmatrix}}\cdots {\begin{Bmatrix}\psi _{N}\end{Bmatrix}}\end{bmatrix}}.$ ⓘ

2 DOF modelini kullanan basit bir örnek kavramların açıklanmasına yardımcı olabilir. Her iki kütlenin kütlesi 1 kg ve her üç yayın sertliği 1000 N/m olsun. Bu problem için kütle ve sertlik matrisi şu şekildedir:

${\begin{bmatrix}M\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\end{bmatrix}}$ ve ${\begin{bmatrix}K\end{bmatrix}}={\begin{bmatrix}2000&-1000\\-1000&2000\end{bmatrix}}.$ ⓘ

O halde ${\begin{bmatrix}A\end{bmatrix}}={\begin{bmatrix}2000&-1000\\-1000&2000\end{bmatrix}}.$ ⓘ

Bu problem için özdeğerler bir özdeğer rutini ile verilir:

${\begin{bmatrix}^{\diagdown }\omega _{r\diagdown }^{2}\end{bmatrix}}={\begin{bmatrix}1000&0\\0&3000\end{bmatrix}}.$ ⓘ

Hertz birimindeki doğal frekanslar o zaman (hatırlayarak $\scriptstyle \omega =2\pi f$) $\scriptstyle f_{1}=5.033\mathrm {\ Hz}$ ve $\scriptstyle f_{2}=8.717{\text{ Hz}}.$ ⓘ

İlgili doğal frekanslar için iki mod şekli aşağıdaki gibi verilmiştir:

${\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}\psi _{1}\end{Bmatrix}}{\begin{Bmatrix}\psi _{2}\end{Bmatrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}-0.707\\-0.707\end{Bmatrix}}_{1}{\begin{Bmatrix}0.707\\-0.707\end{Bmatrix}}_{2}\end{bmatrix}}.$ ⓘ

Sistem 2 DOF'lu bir sistem olduğundan, ilgili doğal frekansları ve şekilleri olan iki mod vardır. Mod şekli vektörleri mutlak hareket değildir, sadece serbestlik derecelerinin göreceli hareketini tanımlar. Bizim durumumuzda ilk mod şekli vektörü, aynı değer ve işarete sahip oldukları için kütlelerin birlikte fazda hareket ettiğini söyler. İkinci mod şekil vektörü durumunda, her bir kütle aynı oranda ters yönde hareket etmektedir. ⓘ

Çoklu DOF probleminin gösterimi

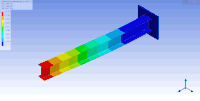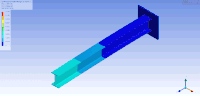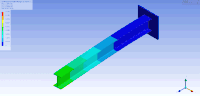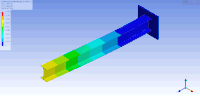
Çok sayıda serbestlik derecesi olduğunda, mod şekillerini görselleştirmenin bir yöntemi de Femap, ANSYS veya ESI Group VA One gibi yapısal analiz yazılımlarını kullanarak bunları canlandırmaktır. Mod şekillerini canlandırmanın bir örneği, ANSYS'de modal analiz kullanılarak gösterildiği gibi konsollu bir I-kiriş için aşağıdaki şekilde gösterilmiştir. Bu durumda, sonlu elemanlar yöntemi, ayrık bir özdeğer problemini çözmek için ilgili nesneyi kafesleyerek kütle ve sertlik matrislerinin bir yaklaşımını oluşturmak için kullanılmıştır. Bu durumda, sonlu elemanlar yönteminin (sonsuz sayıda titreşim modu ve frekansı bulunan) kafeslenmiş yüzeyin bir yaklaşımını sağladığını unutmayın. Bu nedenle, 100'den fazla serbestlik derecesine ve dolayısıyla bir o kadar doğal frekansa ve mod şekline sahip olan bu nispeten basit model, ilk doğal frekanslar ve modlar için iyi bir yaklaşım sağlar. Genel olarak, pratik uygulamalar için sadece ilk birkaç mod önemlidir. ⓘ

ⓘ

Bu tabloda bir I-kirişinin birinci ve ikinci (sırasıyla üst ve alt) yatay eğilme (sol), burulma (orta) ve dikey eğilme (sağ) titreşim modları görselleştirilmiştir. Kirişin sırasıyla yükseklik, genişlik ve uzunluk yönlerinde sıkıştığı/gerildiği başka titreşim modları da mevcuttur.
Konsollu bir I-kirişin mod şekilleri

^ Herhangi bir matematiksel modelin sayısal yaklaşımını gerçekleştirirken, ilgilenilen parametrelerin yakınsamasının tespit edilmesi gerektiğini unutmayın. ⓘ

Tek bir DOF problemine dönüştürülmüş çoklu DOF problemi

Özvektörler, ortogonallik özellikleri olarak adlandırılan çok önemli özelliklere sahiptir. Bu özellikler, çok serbestlik dereceli modellerin çözümünü büyük ölçüde basitleştirmek için kullanılabilir. Özvektörlerin aşağıdaki özelliklere sahip olduğu gösterilebilir:

${\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}},$ ⓘ

${\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}.$ ⓘ

${\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}}$ ve ${\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}$ modların her biri için modal kütle ve sertlik değerlerini içeren köşegen matrislerdir. (Not: Özvektörler (mod şekilleri) keyfi olarak ölçeklendirilebildiğinden, ortogonallik özellikleri genellikle özvektörleri ölçeklendirmek için kullanılır, böylece her mod için modal kütle değeri 1'e eşit olur. Modal kütle matrisi bu nedenle bir kimlik matrisidir) ⓘ

Bu özellikler, aşağıdaki koordinat dönüşümü yapılarak çok serbestlik dereceli modellerin çözümünü büyük ölçüde basitleştirmek için kullanılabilir. ⓘ

${\begin{Bmatrix}x\end{Bmatrix}}={\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}.$ ⓘ

Bu koordinat dönüşümü orijinal serbest titreşim diferansiyel denkleminde kullanıldığında aşağıdaki denklem elde edilir. ⓘ

${\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.$ ⓘ

Ortogonallik özelliklerinden faydalanarak bu denklemin ön çarpımını ${\begin{bmatrix}\Psi \end{bmatrix}}^{T}$ ⓘ

${\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.$ ⓘ

Ortogonallik özellikleri daha sonra bu denklemi basitleştirir:

${\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.$ ⓘ

Bu denklem, çok serbestlik dereceli sistemler için titreşim analizinin temelini oluşturur. Benzer bir sonuç sönümlü sistemler için de elde edilebilir. Buradaki kilit nokta, modal kütle ve sertlik matrislerinin köşegen matrisler olması ve dolayısıyla denklemlerin "ayrıştırılmış" olmasıdır. Başka bir deyişle, problem büyük ve hantal bir çoklu serbestlik derecesi probleminden, yukarıda özetlenen aynı yöntemler kullanılarak çözülebilen birçok tek serbestlik derecesi problemine dönüştürülmüştür. ⓘ

X için çözmenin yerini, modal koordinatlar veya modal katılım faktörleri olarak adlandırılan q için çözme almıştır. ⓘ

Aşağıdakileri anlamak daha açık olabilir ${\begin{Bmatrix}x\end{Bmatrix}}={\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}$ olarak yazılır:

${\begin{Bmatrix}x_{n}\end{Bmatrix}}=q_{1}{\begin{Bmatrix}\psi \end{Bmatrix}}_{1}+q_{2}{\begin{Bmatrix}\psi \end{Bmatrix}}_{2}+q_{3}{\begin{Bmatrix}\psi \end{Bmatrix}}_{3}+\cdots +q_{N}{\begin{Bmatrix}\psi \end{Bmatrix}}_{N}.$ ⓘ

Bu şekilde yazıldığında, serbestlik derecelerinin her birindeki titreşimin mod şekillerinin doğrusal bir toplamı olduğu görülebilir. Ayrıca, her bir modun nihai titreşime ne kadar "katıldığı", modal katılım faktörü olan q ile tanımlanır. ⓘ

Rijit gövde modu

Sınırlandırılmamış çok serbestlik dereceli bir sistem hem rijit gövde ötelemesi ve/veya dönüşü hem de titreşim yaşar. Bir rijit gövde modunun varlığı sıfır doğal frekansla sonuçlanır. Karşılık gelen mod şekline rijit gövde modu denir. ⓘ

Diğer kaynaklar

ⓘ ⓘ

• Thermotron Industries, Fundamentals of Electrodynamic Vibration Testing Handbook
• Nelson Publishing, Evaluation Engineering Magazine ⓘ