İvme

Hızlanma ⓘ
Vakumda (hava direnci yok), Dünya tarafından çekilen nesneler sabit bir oranda hız kazanır.
Yaygın semboller	a
SI birimi	m/s2, m-s-2, m s-2
Türevleri diğer miktarlar	$\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}$

Mekanikte ivme, bir cismin hızının zamana göre değişim oranıdır. İvmeler vektörel büyüklüklerdir (büyüklükleri ve yönleri vardır). Bir nesnenin ivmesinin yönü, o nesneye etki eden net kuvvetin yönü ile verilir. Newton'un İkinci Yasası tarafından tanımlandığı gibi, bir nesnenin ivmesinin büyüklüğü, iki nedenin birleşik etkisidir:

• o nesneye etki eden tüm dış kuvvetlerin net dengesi - büyüklük, ortaya çıkan bu net kuvvetle doğru orantılıdır;
• Nesnenin kütlesi, yapıldığı malzemelere bağlı olarak - büyüklük nesnenin kütlesiyle ters orantılıdır. ⓘ

İvme için SI birimi saniyenin karesi başına metredir (m⋅s-2, ${\tfrac {\operatorname {m} }{\operatorname {s} ^{2}}}$). ⓘ

Örneğin, bir araç durma noktasından başladığında (eylemsiz referans çerçevesinde sıfır hız) ve artan hızlarda düz bir çizgide ilerlediğinde, seyahat yönünde ivmelenir. Araç dönerse, yeni yöne doğru bir ivme meydana gelir ve hareket vektörünü değiştirir. Aracın mevcut hareket yönündeki ivmesine doğrusal (ya da dairesel hareketler sırasında teğetsel) ivme denir ve bu ivmeye araçtaki yolcular kendilerini koltuklarına geri iten bir kuvvet olarak tepki verirler. Yön değiştirirken, etki eden ivme radyal (veya dairesel hareketler sırasında merkezcil) ivme olarak adlandırılır ve yolcular buna merkezkaç kuvveti olarak tepki verir. Aracın hızı azalırsa, bu ters yönde bir ivmedir ve matematiksel olarak negatiftir, bazen yavaşlama veya gecikme olarak adlandırılır ve yolcular yavaşlama tepkisini kendilerini ileri iten bir eylemsizlik kuvveti olarak yaşarlar. Bu tür negatif ivmeler genellikle uzay araçlarında retrorocket yakılmasıyla elde edilir. Hem hızlanma hem de yavaşlama aynı şekilde ele alınır, çünkü her ikisi de hızdaki değişikliklerdir. Bu ivmelerin her biri (teğetsel, radyal, yavaşlama) yolcular tarafından bağıl (diferansiyel) hızları hızdaki değişimden kaynaklanan ivmeye göre nötralize edilene kadar hissedilir. ⓘ

İvme, hızın zamanla değişim hızıdır ve hız grafiğinde herhangi bir noktada, o noktaya teğet doğrunun eğimi olarak tanımlanır. ⓘ

Fizikte ivme, hızın zamana göre türevi olarak tanımlanır. Büyüklüğü uzaklık/zaman² olan bir vektörel niceliktir ve cismin hem hızının hem de yönünün şiddetlerindeki değişimini gösterir. İvmeölçer yardımıyla ölçülen ivmenin SI birimi metre/saniye²'dir. ⓘ

Tanım ve özellikler

Klasik bir parçacığın kinematik büyüklükleri: kütle m, konum r, hız v, ivme a. ⓘ

Ortalama ivme

İvme, hızın değişim oranıdır. Bir yörünge üzerindeki herhangi bir noktada ivmenin büyüklüğü, o noktadaki hızın hem büyüklük hem de yön olarak değişim oranıyla verilir. t zamanındaki gerçek ivme, Δv/Δt'nin Δt → 0 zaman aralığı olarak limitte bulunur ⓘ

Bir nesnenin belirli bir süre boyunca ortalama ivmesi, hızındaki değişimdir, $\Delta \mathbf {v}$'nin dönem süresine bölünmesiyle elde edilir, $\Delta t$. Matematiksel olarak,

$${\bar {\mathbf {a} }}={\frac {\Delta \mathbf {v} }{\Delta t}}.$$

ⓘ

Anlık hızlanma

Aşağıdan yukarıya doğru:

• bir ivme fonksiyonu a(t);
• ivmenin integrali v(t) hız fonksiyonudur;
• ve hızın integrali de s(t) mesafe fonksiyonudur. ⓘ

Bu arada anlık ivme, sonsuz küçük bir zaman aralığındaki ortalama ivmenin limitidir. Kalkülüs terimleriyle, anlık ivme, hız vektörünün zamana göre türevidir:

$$\mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}$$

İvme, hızın, v, t zamanına göre türevi olarak tanımlandığından ve hız da konumun, x, zamana göre türevi olarak tanımlandığından, ivme x'in t'ye göre ikinci türevi olarak düşünülebilir:

$$\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}$$

ⓘ

(Burada ve başka yerlerde, eğer hareket düz bir çizgideyse, vektörel büyüklükler denklemlerde skalerlerle değiştirilebilir). ⓘ

Kalkülüsün temel teoremine göre, ivme fonksiyonu a(t)'nin integralinin hız fonksiyonu v(t) olduğu görülebilir; yani, ivmeye karşı zaman (a'ya karşı t) grafiğinin eğrisinin altındaki alan hız değişimine karşılık gelir.

$$\mathbf {\Delta v} =\int \mathbf {a} \,dt$$

ⓘ

Benzer şekilde, ivme fonksiyonunun türevi olan sarsıntı fonksiyonunun j(t) integrali, belirli bir zamandaki ivme değişimini bulmak için kullanılabilir:

$$\mathbf {\Delta a} =\int \mathbf {j} \,dt$$

ⓘ

Birimler

İvme, hızın (L/T) zamana bölünmesi, yani L T-2 boyutlarına sahiptir. SI ivme birimi saniyenin karesi başına metredir (m s-2); ya da saniyede metre cinsinden hız her saniye ivme değeri kadar değiştiğinden "saniyede metre". ⓘ

Diğer formlar

Dünya'nın yörüngesinde dönen bir uydu gibi dairesel hareket eden bir cisim, hızı sabit olsa da hareket yönünün değişmesi nedeniyle ivmelenir. Bu durumda merkezcil (merkeze doğru) ivmelenme yaşadığı söylenir. ⓘ

Bir cismin serbest düşme durumuna göre ivmesi olan uygun ivme, ivmeölçer adı verilen bir aletle ölçülür. ⓘ

Klasik mekanikte, sabit kütleli bir cisim için, cismin kütle merkezinin (vektör) ivmesi, üzerine etki eden net kuvvet vektörü (yani tüm kuvvetlerin toplamı) ile orantılıdır (Newton'un ikinci yasası):

$$\mathbf {F} =m\mathbf {a} \quad \implies \quad \mathbf {a} ={\frac {\mathbf {F} }{m}}$$

Burada F cisme etki eden net kuvvet, m cismin kütlesi ve a kütle merkezi ivmesidir. Hızlar ışık hızına yaklaştıkça rölativistik etkiler giderek daha büyük hale gelir. ⓘ

Teğetsel ve merkezcil ivme

Hız ve ivme işaretli, salınan bir sarkaç. Hem teğetsel hem de merkezcil ivme yaşar. ⓘ

Kavisli bir hareket için ivme bileşenleri. Teğetsel bileşen at, geçiş hızındaki değişimden kaynaklanır ve eğri boyunca hız vektörü yönünde (veya ters yönde) işaret eder. Normal bileşen (dairesel hareket için merkezcil bileşen olarak da adlandırılır) ac, hız vektörünün yönündeki değişiklikten kaynaklanır ve yörüngeye normaldir, yolun eğrilik merkezine doğru işaret eder. ⓘ

Eğri bir yol üzerinde hareket eden bir parçacığın hızı zamanın bir fonksiyonu olarak şu şekilde yazılabilir:

$\mathbf {v} (t)=v(t){\frac {\mathbf {v} (t)}{v(t)}}=v(t)\mathbf {u} _{\mathrm {t} }(t),$ ⓘ

v(t) yol boyunca seyahat hızına eşittir ve ⓘ

$\mathbf {u} _{\mathrm {t} }={\frac {\mathbf {v} (t)}{v(t)}}\ ,$ ⓘ

zamanda seçilen andaki hareket yönünü işaret eden yola teğet bir birim vektör. Hem değişen v(t) hızı hem de değişen ut yönü dikkate alındığında, eğri bir yol üzerinde hareket eden bir parçacığın ivmesi, iki zaman fonksiyonunun çarpımı için zincirleme türev kuralı kullanılarak şu şekilde yazılabilir:

${\begin{alignedat}{3}\mathbf {a} &={\frac {d\mathbf {v} }{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+v(t){\frac {d\mathbf {u} _{\mathrm {t} }}{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+{\frac {v^{2}}{r}}\mathbf {u} _{\mathrm {n} }\ ,\end{alignedat}}$ ⓘ

Burada un, parçacığın yörüngesinin birim (içe doğru) normal vektörüdür (ana normal olarak da adlandırılır) ve r, t zamanındaki osilasyon çemberine dayanan anlık eğrilik yarıçapıdır. Bu bileşenler teğetsel ivme ve normal veya radyal ivme (veya dairesel harekette merkezcil ivme, ayrıca bkz. dairesel hareket ve merkezcil kuvvet) olarak adlandırılır. ⓘ

Üç boyutlu uzay eğrilerinin geometrik analizi, teğet, (ana) normal ve binormal'i açıklayan Frenet-Serret formülleri ile tanımlanır. ⓘ

Özel durumlar

Düzgün hızlanma

Düzgün bir ivme için hız farkının hesaplanması ⓘ

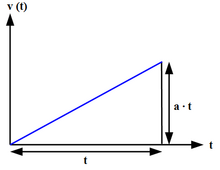
Düzgün veya sabit ivme, bir nesnenin hızının her eşit zaman diliminde eşit miktarda değiştiği bir hareket türüdür. ⓘ

Tekdüze ivmeye sıkça verilen bir örnek, tekdüze bir yerçekimi alanında serbest düşüş halindeki bir cisimdir. Harekete karşı dirençlerin olmadığı durumda düşen bir cismin ivmesi yalnızca yerçekimi alanının gücüne (g) bağlıdır (yerçekimine bağlı ivme olarak da adlandırılır). Newton'un İkinci Yasasına göre kuvvet $\mathbf {F_{g}}$ tarafından verilir:

$\mathbf {F_{g}} =m\mathbf {g}$ ⓘ

Sabit ivme durumunun basit analitik özellikleri nedeniyle, yer değiştirmeyi, başlangıç ve zamana bağlı hızları ve ivmeyi geçen zamanla ilişkilendiren basit formüller vardır:

$\mathbf {s} (t)=\mathbf {s} _{0}+\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}=\mathbf {s} _{0}+{\frac {\mathbf {v} _{0}+\mathbf {v} (t)}{2}}t$

$\mathbf {v} (t)=\mathbf {v} _{0}+\mathbf {a} t$

${v^{2}}(t)={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {s} (t)-\mathbf {s} _{0}]$ ⓘ

burada

• $t$ geçen süredir,
• $\mathbf {s} _{0}$ orijinden ilk yer değiştirmedir,
• $\mathbf {s} (t)$ zamanda orijinden olan yer değiştirmedir $t$,
• $\mathbf {v} _{0}$ başlangıç hızıdır,
• $\mathbf {v} (t)$ zamanındaki hızdır $t$ve
• $\mathbf {a}$ tekdüze hızlanma oranıdır. ⓘ

Özellikle hareket, biri sabit hızda diğeri yukarıdaki denklemlere göre olmak üzere iki ortogonal parçaya ayrılabilir. Galileo'nun gösterdiği gibi, net sonuç parabolik harekettir ve örneğin Dünya yüzeyine yakın bir boşlukta bir merminin yörüngesini tanımlar. ⓘ

Dairesel hareket

Konum vektörü r, her zaman orijinden radyal olarak işaret eder.

Hız vektörü v, her zaman hareket yoluna teğettir.

İvme vektörü a, radyal harekete paralel değildir ancak açısal ve Coriolis ivmeleri tarafından dengelenir, ne de yola teğettir ancak merkezcil ve radyal ivmeler tarafından dengelenir.

Düzlem kutupsal koordinatlarda kinematik vektörler. Düzenin 2 boyutlu uzay ile sınırlı olmadığına dikkat ediniz, ancak herhangi bir yüksek boyutta keyfi bir eğrinin bir noktasında salınan düzlemi temsil edebilir. ⓘ

Düzgün dairesel harekette, yani dairesel bir yol boyunca sabit hızla hareket eden bir parçacık, büyüklüğü sabit kalırken hız vektörünün yönünün değişmesinden kaynaklanan bir ivme yaşar. Bir eğri üzerindeki bir noktanın konumunun zamana göre türevi, yani hızı, her zaman eğriye tam teğet, sırasıyla bu noktadaki yarıçapa ortogonal olarak ortaya çıkar. Düzgün harekette teğet yöndeki hız değişmediğinden, ivme dairenin merkezini işaret eden radyal yönde olmalıdır. Bu ivme, hızın yönünü komşu noktada teğet olacak şekilde sürekli değiştirir ve böylece hız vektörünü daire boyunca döndürür. ⓘ

• Belirli bir hız için $v$geometrik olarak neden olunan bu ivmenin (merkezcil ivme) büyüklüğü yarıçap ile ters orantılıdır $r$ ve bu hızın karesi kadar artar:
  $$a_{c}={\frac {v^{2}}{r}}\;.$$
• Belirli bir açısal hız için $\omega$merkezcil ivme yarıçap ile doğru orantılıdır $r$. Bunun nedeni hızın bağımlı olmasıdır $v$ yarıçap üzerinde $r$.
  $$v=\omega r.$$

Merkezcil ivme vektörünün kutupsal bileşenler cinsinden ifade edilmesi, burada $\mathbf {r}$ dairenin merkezinden parçacığa bu mesafeye eşit büyüklükte bir vektördür ve ivmenin merkeze doğru yönelimi dikkate alındığında ⓘ

$\mathbf {a_{c}} =-{\frac {v^{2}}{|\mathbf {r} |}}\cdot {\frac {\mathbf {r} }{|\mathbf {r} |}}\;.$ ⓘ

Dönüşlerde her zaman olduğu gibi, hız $v$ uzaklığındaki bir noktaya göre açısal hız olarak ifade edilebilir. $r$ olarak ⓘ

$\omega ={\frac {v}{r}}.$ ⓘ

Böylece $\mathbf {a_{c}} =-\omega ^{2}\mathbf {r} \;.$ ⓘ

Bu ivme ve parçacığın kütlesi, bu parçacığı bu düzgün dairesel harekette tutmak için etki eden net kuvvet olarak dairenin merkezine doğru yönlendirilen gerekli merkezcil kuvveti belirler. 'Merkezkaç kuvveti' olarak adlandırılan ve cisim üzerinde dışa doğru etki ediyormuş gibi görünen kuvvet, dairesel hareket halindeki cismin referans çerçevesinde, hareket dairesine teğet bir vektör olan cismin doğrusal momentumuna bağlı olarak deneyimlenen sözde bir kuvvettir. ⓘ

Düzgün olmayan bir dairesel harekette, yani eğri yol boyunca hız değişiyorsa, ivmenin eğriye teğet sıfır olmayan bir bileşeni vardır ve yarıçapı belirleyen, salınım yapan dairenin merkezine yönelen ana normalle sınırlı değildir $r$ merkezcil ivme için. Teğetsel bileşen açısal ivme ile verilir $\alpha$yani, değişim oranı $\alpha ={\dot {\omega }}$ açısal hızın $\omega$ yarıçapın katları $r$. İşte bu, ⓘ

$a_{t}=r\alpha .$ ⓘ

İvmenin teğetsel bileşeninin işareti, açısal ivmenin işareti tarafından belirlenir ($\alpha$) ve teğet her zaman yarıçap vektörüne dik açılarla yönlendirilir. ⓘ

Görelilik ile ilişki

Özel görelilik

Özel görelilik teorisi, boşlukta ışığın hızına yaklaşan hızlarda diğer nesnelere göre hareket eden nesnelerin davranışını açıklar. Newton mekaniğinin, düşük hızlarda büyük bir doğrulukla geçerli olan, gerçeğe tam olarak yaklaşan bir yaklaşım olduğu ortaya çıkmıştır. İlgili hızlar ışık hızına doğru arttıkça, ivme artık klasik denklemleri takip etmez. ⓘ

Hızlar ışık hızına yaklaştıkça, belirli bir kuvvet tarafından üretilen ivme azalır ve ışık hızına yaklaşıldıkça sonsuz derecede küçük hale gelir; kütlesi olan bir nesne bu hıza asimptotik olarak yaklaşabilir, ancak asla ulaşamaz. ⓘ

Genel görelilik

Bir nesnenin hareket durumu bilinmediği sürece, gözlemlenen bir kuvvetin yerçekiminden mi yoksa ivmeden mi kaynaklandığını ayırt etmek imkansızdır - yerçekimi ve eylemsiz ivme aynı etkilere sahiptir. Albert Einstein buna eşdeğerlik ilkesi adını vermiş ve yalnızca yerçekimi kuvveti de dahil olmak üzere hiçbir kuvvet hissetmeyen gözlemcilerin ivmelenmedikleri sonucuna varmakta haklı olduklarını söylemiştir. ⓘ

Dönüşümler

Yaygın ivme birimleri arasında dönüşümler ⓘ

Temel değer	(Gal veya cm/s2)	(ft/s2)	(m/s2)	(Standart yerçekimi, g0)
1 Gal veya cm/s2	1	0.0328084	0.01	1.01972 × 10⁻³
1 ft/s2	30.4800	1	0.304800	0.0310810
1 m/s2	100	3.28084	1	0.101972
1 g0	980.665	32.1740	9.80665	1

Kütleçekim ivmesi

İvme kütleçekim sebebiyle de ortaya çıkar. Dünya simetrik bir küre olmadığı için, deniz seviyesinde kütleçekimi her yerde aynı değildir. Mesela Paris kentinde ivme; ⓘ

$\quad g=9.80665\quad m/sn^{2}$ ⓘ