Yamuk

Trapezium (BrE) Yamuk (AmE) ⓘ
Yamuk veya trapezoid
Tip	dörtgen
Kenarlar ve köşeler	4
Alan	${\tfrac {a+b}{2}}h$
Mülkler	dışbükey

En az bir çift paralel kenarı olan bir dörtgen, Amerikan ve Kanada İngilizcesinde yamuk (/ˈtræpəzɔɪd/) olarak adlandırılır. İngilizcede ve İngilizcenin diğer biçimlerinde (Kuzey Amerika) yamuğa trapezium (/trəˈpiːziəm/) denir. Bu iki terimin yer değiştirmesi Charles Hutton'un matematik sözlüğündeki bir hatanın sonucudur. ⓘ

Bir yamuk, Öklid geometrisinde zorunlu olarak dışbükey bir dörtgendir. Paralel kenarlara yamuğun tabanları denir. Diğer iki kenar paralel değilse bacak (ya da yanal kenar) olarak adlandırılır; aksi takdirde yamuk bir paralelkenardır ve iki çift taban vardır). Skalen yamuk, aşağıdaki özel durumların aksine, eşit ölçülü kenarları olmayan bir yamuktur. ⓘ

Etimoloji ve yamuk ile trapez

Hutton'ın 1795'teki hatası ⓘ

Antik Yunan matematikçi Öklid, dördü iki paralel kenar kümesine sahip (İngilizce'de kare, dikdörtgen, eşkenar dörtgen ve eşkenar dörtgen olarak bilinir) ve sonuncusu iki paralel kenar kümesine sahip olmayan beş tip dörtgen tanımladı - bir τραπέζια (trapezia kelimenin tam anlamıyla "bir masa", kendisi τετράς (tetrás), "dört" + πέζα (péza), "bir ayak; uç, sınır, kenar"). ⓘ

Proclus (MS 412 ila 485) tarafından Öklid'in Elementler'inin ilk kitabına yazdığı yorumda iki tür trapezia tanıtılmıştır:

• bir çift paralel kenar - bir trapez (τραπέζιον), ikizkenar (eşit bacaklar) ve skalen (eşit olmayan) trapezlere ayrılır
• paralel kenarı yok - yamuk (τραπεζοειδή, trapezoeidé, kelimenin tam anlamıyla yamuk benzeri (εἶδος "benzer" anlamına gelir), aynı şekilde küp küp benzeri ve eşkenar dörtgen eşkenar dörtgen benzeri anlamına gelir) ⓘ

Charles Hutton tarafından 1795 yılında yayınlanan etkili bir matematik sözlüğü, terimlerin yer değiştirmesini açıklama yapmadan destekleyene kadar, tüm Avrupa dilleri 18. yüzyılın sonlarına kadar İngilizcede olduğu gibi Proclus'un yapısını takip etmiştir. Bu hata İngiliz İngilizcesinde yaklaşık 1875 yılında düzeltilmiş, ancak Amerikan İngilizcesinde günümüze kadar korunmuştur. ⓘ

Tip	Resim	Orijinal terminoloji			Modern terminoloji ⓘ
		Öklid (Tanım 22)	Proclus (Tanımlar 30-34, Posidonius'tan alıntı)	Euclid / Proclus tanımı	İngiliz İngilizcesi (ve Avrupa dilleri)	Amerikan İngilizcesi
Paralelkenar		ῥόμβος (rhombos)		eşkenar ama dik açılı değil	Rhombus		Yamuk (dahil)
		ῥομβοειδὲς (rhomboides)		karşılıklı kenarlar ve açılar birbirine eşittir ancak eşkenar veya dik açılı değildir	Rhomboid (halk dilinde Paralelkenar)
Paralelkenar olmayan		τραπέζια (trapezia)	τραπέζιον ἰσοσκελὲς (trapezion isoskelés)	İki paralel kenar ve bir simetri çizgisi	Isoceles Trapezium	İzosel Trapezoid
			τραπέζιον σκαληνὸν (trapezion skalinón)	İki paralel kenar ve simetri çizgisi yok	Trapezium	Trapezoid (özel)
			τραπέζοειδὲς (trapezoides)	Paralel kenar yok	Trapezoid	Trapezium

Bu şekil genellikle düzensiz dörtgen olarak adlandırılır. ⓘ

Kapsayıcı vs özel tanım

İki çift paralel kenarı olan paralelkenarların yamuk olarak kabul edilip edilmeyeceği konusunda bazı anlaşmazlıklar vardır. Bazıları yamuğu sadece bir çift paralel kenarı olan bir dörtgen olarak tanımlar (dışlayıcı tanım) ve böylece paralelkenarları hariç tutar. Diğerleri ise yamuğu en az bir çift paralel kenarı olan bir dörtgen olarak tanımlar (kapsayıcı tanım) ve paralelkenarı özel bir yamuk türü haline getirir. İkinci tanım, kalkülüs gibi yüksek matematikteki kullanımlarıyla tutarlıdır. Bu makale kapsayıcı tanımı kullanmakta ve paralelkenarları yamuğun özel durumları olarak değerlendirmektedir. Bu aynı zamanda dörtgenlerin taksonomisinde de savunulmaktadır. ⓘ

Kapsayıcı tanım altında, tüm paralelkenarlar (eşkenar dörtgenler, dikdörtgenler ve kareler dahil) yamuktur. Dikdörtgenler orta kenarlarda ayna simetrisine sahiptir; eşkenar dörtgenler köşelerde ayna simetrisine sahipken, kareler hem orta kenarlarda hem de köşelerde ayna simetrisine sahiptir. ⓘ

Özel durumlar

Yamuk özel durumları. Turuncu şekiller aynı zamanda paralelkenar olarak da nitelendirilir. ⓘ

Bir dik yamuk (dik açılı yamuk olarak da adlandırılır) iki bitişik dik açıya sahiptir. Dik yamuklar, bir eğrinin altındaki alanları tahmin etmek için trapezoidal kuralda kullanılır. ⓘ

Bir dar yamuğun uzun taban kenarında iki bitişik dar açı bulunurken, bir geniş yamuğun her tabanında bir dar ve bir geniş açı bulunur. ⓘ

İkizkenar yamuk, taban açılarının aynı ölçüye sahip olduğu bir yamuktur. Sonuç olarak iki bacak da eşit uzunluktadır ve yansıma simetrisine sahiptir. Bu, dar yamuklar veya dik yamuklar (dikdörtgenler) için mümkündür. ⓘ

Paralelkenar, iki çift paralel kenarı olan bir yamuktur. Bir paralelkenar merkezi 2 kat dönme simetrisine (veya nokta yansıma simetrisine) sahiptir. Geniş yamuklar veya dik yamuklar (dikdörtgenler) için mümkündür. ⓘ

Teğetsel yamuk, bir daire içine sahip olan bir yamuktur. ⓘ

Bir Saccheri dörtgeni, Öklid düzleminde bir dikdörtgen iken, iki bitişik dik açı ile hiperbolik düzlemdeki bir yamuğa benzer. Hiperbolik düzlemdeki bir Lambert dörtgeninin 3 dik açısı vardır. ⓘ

Var olma koşulu

Dört a, c, b, d uzunluğu, a ve b'nin paralel olduğu paralelkenar olmayan bir yamuğun ardışık kenarlarını ancak aşağıdaki durumlarda oluşturabilir

$\displaystyle |d-c|<|b-a|<d+c.$ ⓘ

Aşağıdaki durumlarda dörtgen bir paralelkenardır $d-c=b-a=0$'dir, ancak aşağıdaki durumlarda bir dış teğet dörtgendir (yamuk değildir) $|d-c|=|b-a|\neq 0$. ⓘ

Karakterizasyonlar

genel yamuk/trapez:
paralel kenarlar: $a,\,b$ ile $a<b$
Bacaklar: $c,\,d$
çaprazlar: $q,\,p$
orta bölüm: $m$
yükseklik/yükseklik: $h$ ⓘ

karşıt üçgenlere sahip yamuk/trapezium $S,\,T$ köşegenler tarafından oluşturulan ⓘ

Dışbükey bir dörtgen verildiğinde, aşağıdaki özellikler eşdeğerdir ve her biri dörtgenin bir yamuk olduğunu ima eder:

• Birbirini tamamlayan, yani toplamı 180 derece olan iki bitişik açıya sahiptir.
• Bir kenar ile bir köşegen arasındaki açı, karşı kenar ile aynı köşegen arasındaki açıya eşittir.
• Köşegenler birbirlerini karşılıklı olarak aynı oranda keser (bu oran paralel kenarların uzunlukları arasındaki oranla aynıdır).
• Köşegenler dörtgeni, karşılıklı bir çiftinin alanları eşit olan dört üçgene böler.
• Bir köşegen tarafından oluşturulan iki üçgenin alanlarının çarpımı, diğer köşegen tarafından oluşturulan iki üçgenin alanlarının çarpımına eşittir.
• Köşegenlerin oluşturduğu dört üçgenin bazı karşılıklı iki üçgeninin S ve T alanları denklemi sağlar ⓘ

${\sqrt {K}}={\sqrt {S}}+{\sqrt {T}},$ ⓘ

Burada K dörtgenin alanıdır. ⓘ

• Karşılıklı iki kenarın orta noktaları ve köşegenlerin kesişme noktaları aynı hizadadır.
• ABCD dörtgenindeki açılar aşağıdakileri sağlar $\sin A\sin C=\sin B\sin D.$
• İki komşu açının kosinüsleri, diğer iki açının kosinüsleri gibi 0'a eşittir.
• İki komşu açının kotanjantları, diğer iki komşu açının kotanjantları gibi 0'a eşittir.
• Bir bimedyen dörtgeni eşit alanlı iki dörtgene böler.
• Karşılıklı iki kenarın orta noktalarını birleştiren bimedyanın uzunluğunun iki katı, diğer kenarların uzunluklarının toplamına eşittir. ⓘ

Ek olarak, aşağıdaki özellikler eşdeğerdir ve her biri a ve b karşıt kenarlarının paralel olduğunu ima eder:

• Ardışık a, c, b, d kenarları ve p, q köşegenleri aşağıdaki denklemi sağlar

$p^{2}+q^{2}=c^{2}+d^{2}+2ab.$ ⓘ

• Köşegenlerin orta noktaları arasındaki v mesafesi denklemi karşılar

$v={\frac {|a-b|}{2}}.$ ⓘ

Orta bölüm ve yükseklik

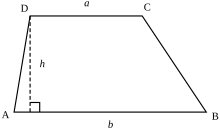
Bir yamuğun orta bölümü (medyan veya orta çizgi olarak da adlandırılır) bacakların orta noktalarını birleştiren bölümdür. Tabanlara paraleldir. Uzunluğu m, yamuğun a ve b tabanlarının uzunluklarının ortalamasına eşittir,

$m={\frac {a+b}{2}}.$ ⓘ

Bir yamuğun orta bölümü iki bimedyandan biridir (diğer bimedyan yamuğu eşit alanlara böler). ⓘ

Yükseklik (veya irtifa) tabanlar arasındaki dik mesafedir. İki tabanın farklı uzunluklara sahip olması durumunda (a ≠ b), yamuğun yüksekliği h, aşağıdaki formül kullanılarak dört kenarının uzunluğuna göre belirlenebilir

$h={\frac {\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}}$ ⓘ

Burada c ve d bacakların uzunluklarıdır. ⓘ

Alan

Bir yamuğun K alanı şu şekilde verilir

$K={\frac {a+b}{2}}\cdot h=mh$ ⓘ

Burada a ve b paralel kenarların uzunlukları, h yükseklik (bu kenarlar arasındaki dik mesafe) ve m iki paralel kenarın uzunluklarının aritmetik ortalamasıdır. MS 499'da Hint matematiğinin ve Hint astronomisinin klasik çağından büyük bir matematikçi-astronom olan Aryabhata, Aryabhatiya'da bu yöntemi kullanmıştır (bölüm 2.8). Bu, özel bir durum olarak, bir üçgeni paralel kenarlarından birinin bir noktaya küçüldüğü dejenere bir yamuk olarak düşünerek, bir üçgenin alanı için iyi bilinen formülü verir. ⓘ

7. yüzyılda yaşamış Hintli matematikçi I. Bhāskara, a, c, b, d ardışık kenarlarına sahip bir yamuğun alanı için aşağıdaki formülü türetmiştir:

$K={\frac {1}{2}}(a+b){\sqrt {c^{2}-{\frac {1}{4}}\left((b-a)+{\frac {c^{2}-d^{2}}{b-a}}\right)^{2}}}$ ⓘ

Burada a ve b paraleldir ve b > a'dır. Bu formül daha simetrik bir versiyona dönüştürülebilir

$K={\frac {a+b}{4|b-a|}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}.$ ⓘ

Paralel kenarlardan biri bir noktaya kadar küçüldüğünde (diyelim ki a = 0), bu formül Heron'un üçgenin alanı için kullandığı formüle indirgenir. ⓘ

Alan için Heron'un formülüne daha çok benzeyen bir başka eşdeğer formül de şudur

$K={\frac {a+b}{|b-a|}}{\sqrt {(s-b)(s-a)(s-b-c)(s-b-d)}},$ ⓘ

nerede $s={\tfrac {1}{2}}(a+b+c+d)$ yamuğun yarı ölçüsüdür. (Bu formül Brahmagupta'nın formülüne benzer, ancak bir yamuğun döngüsel olmaması (bir çemberin içine yazılmamış olması) nedeniyle ondan farklıdır. Bu formül aynı zamanda Bretschneider'in genel dörtgen formülünün özel bir durumudur). ⓘ

Bretschneider'ın formülünden şu sonuç çıkar

$K={\sqrt {{\frac {(ab^{2}-a^{2}b-ad^{2}+bc^{2})(ab^{2}-a^{2}b-ac^{2}+bd^{2})}{4(b-a)^{2}}}-\left({\frac {c^{2}+d^{2}-a^{2}-b^{2}}{4}}\right)^{2}}}.$ ⓘ

Paralel kenarların orta noktalarını birleştiren doğru, alanı ikiye böler. ⓘ

Yamuğun alanı "K" ile gösterilir. a ve b kenarlarının toplamının ikiye bölümünün yükseklik ile çarpılmasıyla hesaplanır. Formülü ise şöyledir;$K={\frac {a+b}{2}}\cdot h$

ⓘ

Diyagonaller

Köşegenlerin uzunlukları şöyledir

$p={\sqrt {\frac {ab^{2}-a^{2}b-ac^{2}+bd^{2}}{b-a}}},$

$q={\sqrt {\frac {ab^{2}-a^{2}b-ad^{2}+bc^{2}}{b-a}}}$ ⓘ

Burada a kısa taban, b uzun taban, c ve d ise yamuğun bacaklarıdır. ⓘ

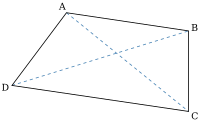
Yamuk, O noktasında kesişen AC ve BD köşegenleri (sağda gösterildiği gibi) tarafından dört üçgene bölünürse, o zaman $\triangle$ AOD aşağıdakilere eşittir $\triangle$ BOC, ve aşağıdaki alanların ürünüdür $\triangle$ AOD ve $\triangle$ BOC'unkine eşittir $\triangle$ AOB ve $\triangle$ COD. Her bir komşu üçgen çiftinin alanlarının oranı, paralel kenarların uzunlukları arasındaki oranla aynıdır. ⓘ

Yamuğun köşeleri sırayla A, B, C ve D olsun ve AB ve DC paralel kenarlara sahip olsun. E köşegenlerin kesişimi olsun ve F DA kenarında ve G BC kenarında olsun, öyle ki FEG AB ve CD'ye paralel olsun. O halde FG, AB ve DC'nin harmonik ortalamasıdır:

${\frac {1}{FG}}={\frac {1}{2}}\left({\frac {1}{AB}}+{\frac {1}{DC}}\right).$ ⓘ

Hem genişletilmiş paralel olmayan kenarların kesişme noktasından hem de köşegenlerin kesişme noktasından geçen doğru, her bir tabanı ikiye böler. ⓘ

Diğer özellikler

Alan merkezi (düzgün bir lamina için kütle merkezi), paralel kenarların orta noktalarını birleştiren doğru parçası boyunca, aşağıdaki şekilde verilen uzun kenardan x dik uzaklığında yer alır

$x={\frac {h}{3}}\left({\frac {2a+b}{a+b}}\right).$ ⓘ

Alanın merkezi bu segmenti şu oranda böler (kısa kenardan uzun kenara doğru alındığında) ⓘ

${\frac {a+2b}{2a+b}}.$ ⓘ

A ve B açıortayları P'de kesişiyorsa ve C ve D açıortayları Q'da kesişiyorsa, o zaman

$PQ={\frac {|AD+BC-AB-CD|}{2}}.$ ⓘ

Uygulamalar

New York'taki Metropolitan Sanat Müzesi'nde bulunan Dendur Tapınağı ⓘ

Mimarlık

Mimaride bu kelime simetrik kapılar, pencereler ve Mısır tarzında tabanda daha geniş, tepeye doğru daralan binalar için kullanılır. Bunların düz kenarları ve keskin köşeleri varsa, şekilleri genellikle ikizkenar yamuktur. Bu, İnkaların kapı ve pencereleri için standart stildi. ⓘ

Geometri

Çapraz merdivenler problemi, köşegen uzunlukları ve dik bacaktan köşegen kesişimine kadar olan mesafe verildiğinde, bir dik yamuğun paralel kenarları arasındaki mesafeyi bulma problemidir. ⓘ

Biyoloji

Sütleğen böceği üzerinde ana hatları belirlenmiş trapeziform pronotum örneği ⓘ

Morfoloji, taksonomi ve bu tür şekiller için bir terimin gerekli olduğu diğer tanımlayıcı disiplinlerde, trapezoidal veya trapeziform gibi terimler genellikle belirli organların veya formların tanımlanmasında yararlıdır. ⓘ

Bilgisayar mühendisliği

Bilgisayar mühendisliğinde, özellikle dijital mantık ve bilgisayar mimarisinde, yamuklar tipik olarak çoklayıcıları sembolize etmek için kullanılır. Çoklayıcılar, birden fazla eleman arasında seçim yapan ve bir seçim sinyaline dayalı olarak tek bir çıkış üreten mantık elemanlarıdır. Tipik tasarımlar, evrensel olarak eşdeğer oldukları için özellikle çoklayıcı olduklarını belirtmeden yamuklar kullanacaktır. ⓘ