Dikdörtgen

Dikdörtgen ⓘ
Dikdörtgen ⓘ
	Dikdörtgen
Tip	dörtgen, yamuk, paralelkenar, ortotop
Kenarlar ve köşeler	4
Schläfli sembolü	{ } × { }
Coxeter-Dynkin diyagramları
Simetri grubu	Dihedral (D2), [2], (*22), sıra 4
Mülkler	dışbükey, izogonal, döngüsel Karşıt açılar ve kenarlar uyumludur

ABCD dikdörtgeninin köşegenlerinin ve dik açılarından biri olan C açısının gösterimi ⓘ

Dikdörtgen, karşılıklı kenarları birbirine eşit, dik ve paralel olan dörtgene denir. ⓘ

Bir dikdörtgende, karşılıklı kenarların orta noktalarını birleştiren birbirine dik iki simetri ekseni vardır. Bu eksenlerin kesim noktası aynı zamanda köşegenlerin de kesim noktasıdır, bu noktaya simetri merkezi denir. Dikdörtgenin dört açısı da dik açıdır ve köşegenleri birbirine eşittir. Dikdörtgenin alanı, tabanı ile yüksekliğinin çarpımına eşittir. Eski adı ise mustatil'dir. ⓘ

Alan = a x b ⓘ

Dikdörtgen kelimesi Latince rectus (sıfat olarak, doğru, uygun) ve angulus (açı) kelimelerinin birleşiminden oluşan rectangulus kelimesinden gelmektedir. ⓘ

Dikdörtgenler, düzlemin dikdörtgenlerle döşenmesi veya bir dikdörtgenin çokgenlerle döşenmesi gibi birçok döşeme probleminde yer alır. ⓘ

Karakterizasyonlar

Dışbükey bir dörtgen, ancak ve ancak aşağıdakilerden herhangi biri ise bir dikdörtgendir:

en az bir dik açıya sahip bir paralelkenar
köşegenleri eşit uzunlukta olan bir paralelkenar
ABD ve DCA üçgenlerinin eş olduğu bir ABCD paralelkenarı
bir eşkenar dörtgen
dört dik açılı bir dörtgen
iki köşegenin eşit uzunlukta olduğu ve birbirini ikiye böldüğü bir dörtgen
a, b, c, d ardışık kenarları olan dışbükey bir dörtgenin alanı ${\tfrac {1}{4}}(a+c)(b+d)$ .
a, b, c, d ardışık kenarları olan dışbükey bir dörtgenin alanı ${\tfrac {1}{2}}{\sqrt {(a^{2}+c^{2})(b^{2}+d^{2})}}.$ ⓘ

Sınıflandırma

Dikdörtgen hem paralelkenarın hem de yamuğun özel bir durumudur. Kare, dikdörtgenin özel bir durumudur. ⓘ

Geleneksel hiyerarşi

Dikdörtgen, her bir bitişik kenar çiftinin dik olduğu paralelkenarın özel bir durumudur. ⓘ

Paralelkenar, trapezin (Kuzey Amerika'da yamuk olarak bilinir) her iki karşıt kenar çiftinin paralel ve eşit uzunlukta olduğu özel bir durumudur. ⓘ

Trapez, en az bir çift paralel karşılıklı kenarı olan dışbükey bir dörtgendir. ⓘ

Dışbükey bir dörtgen

Basit: Sınır kendi kendini geçmez.
Yıldız şekilli: Tüm iç kısım, herhangi bir kenarı geçmeden tek bir noktadan görülebilir. ⓘ

Alternatif hiyerarşi

De Villiers dikdörtgeni daha genel olarak, simetri eksenleri her bir karşılıklı kenar çiftinden geçen herhangi bir dörtgen olarak tanımlar. Bu tanım hem dik açılı dikdörtgenleri hem de çapraz dikdörtgenleri içerir. Her birinin bir çift karşıt kenara paralel ve eşit uzaklıkta bir simetri ekseni ve bu kenarların dik açıortayı olan başka bir ekseni vardır, ancak çapraz dikdörtgen durumunda, ilk eksen, ikiye böldüğü her iki kenar için de bir simetri ekseni değildir. ⓘ

Her biri bir çift zıt kenardan geçen iki simetri eksenine sahip dörtgenler, bir çift zıt kenardan geçen en az bir simetri eksenine sahip daha büyük dörtgenler sınıfına aittir. Bu dörtgenler ikizkenar trapezleri ve çapraz ikizkenar trapezleri (ikizkenar trapezlerle aynı köşe düzenine sahip çapraz dörtgenler) içerir. ⓘ

Mülkler

Simetri

Bir dikdörtgen döngüseldir: tüm köşeleri tek bir daire üzerinde yer alır. ⓘ

Eşkenar dörtgendir: tüm köşe açıları eşittir (her biri 90 derecedir). ⓘ

İzogonal veya köşe geçişlidir: tüm köşeler aynı simetri yörüngesi içinde yer alır. ⓘ

İki yansıma simetrisi çizgisine ve 2. dereceden (180° boyunca) dönme simetrisine sahiptir. ⓘ

Dikdörtgen-eşkenar dörtgen ikiliği

Bir dikdörtgenin çift çokgeni, aşağıdaki tabloda gösterildiği gibi bir eşkenar dörtgendir. ⓘ

Dikdörtgen	Eşkenar Dörtgen ⓘ
Tüm açılar eşittir.	Tüm kenarlar eşittir.
Alternatif kenarlar eşittir.	Alternatif açılar eşittir.
Merkezi köşelerinden eşit uzaklıktadır, dolayısıyla bir çemberi vardır.	Merkezi kenarlarından eşit uzaklıktadır, dolayısıyla bir iç çemberi vardır.
İki simetri ekseni karşıt kenarları ikiye böler.	İki simetri ekseni karşıt açıları ikiye böler.
Köşegenlerin uzunlukları eşittir.	Köşegenler eşit açılarla kesişir.

Bir dikdörtgenin kenarlarının orta noktalarının sırayla birleştirilmesiyle oluşan şekil eşkenar dörtgendir ve bunun tersi de geçerlidir. ⓘ

Çeşitli

Dikdörtgen doğrusal bir çokgendir: kenarları dik açılarla birleşir. ⓘ

Düzlemdeki bir dikdörtgen, örneğin konum için üç (iki öteleme ve bir dönme olmak üzere), şekil için bir (en-boy oranı) ve toplam boyut (alan) için bir olmak üzere beş bağımsız serbestlik derecesi ile tanımlanabilir. ⓘ

Hiçbiri diğerinin içine sığmayan iki dikdörtgenin karşılaştırılamaz olduğu söylenir. ⓘ

Formüller

Bir dikdörtgenin çevre uzunluğu için formül ⓘ

Bir dikdörtgenin alanı, uzunluk ve genişliğin çarpımıdır. ⓘ

Eğer bir dikdörtgenin uzunluğu $\ell$ ve genişlik $w$

alanı var $A=\ell w\,$ ,
çevresi var $P=2\ell +2w=2(\ell +w)\,$ ,
her köşegen uzunluğa sahiptir $d={\sqrt {\ell ^{2}+w^{2}}}$ ,
ve ne zaman $\ell =w\,$ 'de dikdörtgen bir karedir. ⓘ

Teoremler

Dikdörtgenler için izoperimetrik teorem, belirli bir çevreye sahip tüm dikdörtgenler arasında karenin en büyük alana sahip olduğunu belirtir. ⓘ

Köşegenleri dik olan herhangi bir dörtgenin kenarlarının orta noktaları bir dikdörtgen oluşturur. ⓘ

Köşegenleri eşit olan bir paralelkenar bir dikdörtgendir. ⓘ

Döngüsel dörtgenler için Japon teoremi, döngüsel bir dörtgenin köşeleri tarafından belirlenen dört üçgenin her seferinde üçü alındığında bir dikdörtgen oluşturduğunu belirtir. ⓘ

İngiliz bayrak teoremi, köşeleri A, B, C ve D olarak gösterilen bir dikdörtgenin aynı düzlemi üzerindeki herhangi bir P noktası için şunu belirtir:

\displaystyle (AP)^{2}+(CP)^{2}=(BP)^{2}+(DP)^{2}.

ⓘ

Düzlemdeki her dışbükey C cismi için, C'ye öyle bir r dikdörtgeni çizebiliriz ki, r'nin homotetik bir kopyası R, C'yi çevreler ve pozitif homotetiklik oranı en fazla 2 ve $0.5{\text{ × Area}}(R)\leq {\text{Area}}(C)\leq 2{\text{ × Area}}(r)$ . ⓘ

Çapraz dikdörtgenler

Çapraz dörtgen (kendisiyle kesişen), kendisiyle kesişmeyen bir dörtgenin iki köşegeniyle birlikte karşılıklı iki kenarından oluşur. Benzer şekilde, çapraz dikdörtgen, iki köşegenle birlikte bir dikdörtgenin karşılıklı iki kenarından oluşan çapraz bir dörtgendir. Dikdörtgen ile aynı köşe düzenine sahiptir. Ortak bir tepe noktasına sahip iki özdeş üçgen gibi görünür, ancak geometrik kesişme bir tepe noktası olarak kabul edilmez. ⓘ

Çapraz dörtgen bazen bir papyona veya kelebeğe benzetilir, bazen de "açısal sekiz" olarak adlandırılır. Bükülmüş üç boyutlu bir dikdörtgen tel çerçeve papyon şeklini alabilir. ⓘ

Çapraz bir dikdörtgenin iç kısmı, saat yönünde veya saat yönünün tersine sarım yönüne bağlı olarak her üçgende ±1'lik bir çokgen yoğunluğuna sahip olabilir. ⓘ

Sağa ve sola dönüşlere izin verildiği takdirde çapraz dikdörtgen eşkenar dörtgen olarak kabul edilebilir. Herhangi bir çapraz dörtgende olduğu gibi, iç açılarının toplamı 720°'dir ve iç açıların dışta görünmesine ve 180°'yi aşmasına izin verir. ⓘ

Bir dikdörtgen ve bir çapraz dikdörtgen aşağıdaki ortak özelliklere sahip dörtgenlerdir:

Karşılıklı kenarların uzunlukları eşittir.
İki köşegenin uzunluğu eşittir.
İki yansıma simetrisi çizgisine ve 2. dereceden (180° boyunca) dönme simetrisine sahiptir. ⓘ

Diğer dikdörtgenler

Bir eyer dikdörtgeni, bir küboidin köşelerinden dönüşümlü olarak 4 düzlemsel olmayan köşeye sahiptir ve dört köşenin doğrusal bir kombinasyonu olarak tanımlanan benzersiz bir minimal yüzey iç kısmı ile bir eyer yüzeyi oluşturur. Bu örnekte dikdörtgenin 4 mavi kenarı ve hepsi küboid dikdörtgen yüzlerin köşegenleri olan iki yeşil köşegen gösterilmektedir. ⓘ

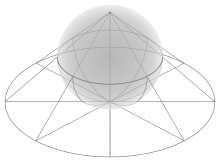
Küresel geometride, küresel bir dikdörtgen, dört kenarı 90°'den büyük eşit açılarda buluşan büyük daire yayları olan bir şekildir. Karşılıklı yayların uzunlukları eşittir. Öklid katı geometrisindeki bir kürenin yüzeyi, eliptik geometri anlamında Öklid dışı bir yüzeydir. Küresel geometri, eliptik geometrinin en basit şeklidir. ⓘ

Eliptik geometride eliptik dikdörtgen, dört kenarı 90°'den büyük eşit açılarda buluşan eliptik yaylar olan eliptik düzlemdeki bir şekildir. Karşılıklı yayların uzunlukları eşittir. ⓘ

Hiperbolik geometride hiperbolik dikdörtgen, hiperbolik düzlemde dört kenarı 90°'den küçük eşit açılarda buluşan hiperbolik yaylar olan bir şekildir. Karşılıklı yayların uzunlukları eşittir. ⓘ

Mozaiklemeler

Dikdörtgen birçok periyodik mozaikleme deseninde, örneğin tuğla işçiliğinde kullanılır:

Yığma bağ	Koşu bağı	Sepet örgüsü	Sepet örgüsü	Balıksırtı deseni ⓘ

Kare, mükemmel ve diğer döşenmiş dikdörtgenler

Mertebesi 9 olan mükemmel bir dikdörtgen ⓘ

Kareler, dikdörtgenler veya üçgenlerle döşenmiş bir dikdörtgenin sırasıyla "kareli", "dikdörtgenli" veya "üçgenli" (veya "üçgenli") bir dikdörtgen olduğu söylenir. Karoların benzer ve sonlu sayıda olması ve hiçbir karonun aynı boyutta olmaması durumunda karolu dikdörtgen mükemmeldir. Böyle iki karo aynı boyuttaysa, döşeme kusurludur. Mükemmel (veya kusurlu) üçgen dikdörtgende üçgenler dik üçgen olmalıdır. Bilinen tüm mükemmel dikdörtgenler, mükemmel kareler ve ilgili şekillerden oluşan bir veritabanı squaring.net adresinde bulunabilir. Bir dikdörtgenin mükemmel bir şekilde döşenmesi için gereken en düşük kare sayısı 9'dur ve bir karenin mükemmel bir şekilde döşenmesi için gereken en düşük sayı 21'dir ve 1978 yılında bilgisayar araştırması ile bulunmuştur. ⓘ

Bir dikdörtgen, ancak ve ancak sonlu sayıda eşit olmayan kare ile döşenebilirse orantılı kenarlara sahiptir. Aynı durum, döşemelerin eşit olmayan ikizkenar dik üçgenler olması halinde de geçerlidir. ⓘ

Dikdörtgenlerin en çok dikkat çeken diğer döşemeler tarafından eğilmesi, tüm dönüşlere ve yansımalara izin veren eşkenar dikdörtgen olmayan poliominolar tarafından yapılanlardır. Ayrıca uyumlu poliabololar tarafından yapılan eğimler de vardır. ⓘ

Unicode

U+25AC ▬ SIYAH DIKDÖRTGEN

   U+25AD ▭ BEYAZ DIKDÖRTGEN
   U+25AE ▮ SIYAH DIKEY DIKDÖRTGEN
   U+25AF ▯ BEYAZ DIKEY DIKDÖRTGEN ⓘ