Yerçekimi

Dünyanın NASA'nın GRACE misyonunda ölçülen yerçekimi, ideal düz bir Yerküre'nin teorik çekimden farkı göstermektedir. Bu ideal şekle Dünya elipsoidi denir. Kırmızı bölgeler, çekimin idealden fazla olduğu yerleri, mâvi bölgeler de daha hafif olduğu yerlerdir.

Yer çekimi, Dünya'nın kütleçekimidir. Dünya yüzeyinde veya yakınındaki nesneleri etkiler ve onlara yer çekimi ivmesini kazandırır. Dünya yüzeyinde tüm cisimler bu ivme ile düşerler (düşen cisim denklemleri). İvmenin Paris'teki değeri tam olarak 9,80665 m/s² dir. M kütlesine sahip bir cisme doğru olan yerçekimi ivmesi ⓘ

$g={MG \over r^{2}}$ ⓘ

formülüyle hesaplanır. ⓘ

Dünya'nın yerçekimi, g ile gösterilir, yerçekiminin (Dünya içindeki kütle dağılımından) ve merkezkaç kuvvetinin (Dünya'nın dönüşünden) birleşik etkisi nedeniyle nesnelere verilen net ivmedir. Yönü bir çekül ile çakışan ve kuvveti veya büyüklüğü norm tarafından verilen bir vektör (fizik) niceliğidir $g=\|{\mathit {\mathbf {g} }}\|$. ⓘ

SI birimlerinde bu ivme saniyenin karesi başına metre (sembollerle, m/s² veya m-s-2) veya eşdeğer olarak kilogram başına newton (N/kg veya N-kg-1) olarak ifade edilir. Dünya yüzeyine yakın yerlerde yerçekimi ivmesi yaklaşık 9,81 m/s² (32,2 ft/s²)'dir, bu da hava direncinin etkileri göz ardı edildiğinde serbest düşen bir nesnenin hızının her saniye yaklaşık 9,81 metre (32,2 ft) artacağı anlamına gelir. Bu miktar bazen gayri resmi olarak küçük g olarak adlandırılır (buna karşılık, yerçekimi sabiti G büyük G olarak adlandırılır). ⓘ

Dünya'nın yerçekiminin kesin gücü konuma bağlı olarak değişir. Dünya yüzeyinde standart yerçekimi olarak bilinen nominal "ortalama" değer, tanım gereği 9,80665 m/s²'dir (32,1740 ft/s²). Bu miktar çeşitli şekillerde gn, ge (bu bazen Dünya'daki normal ekvatoral değer olan 9,78033 m/s² (32,0877 ft/s²) anlamına gelir), g₀, gee veya sadece g (değişken yerel değer için de kullanılır) olarak gösterilir. ⓘ

Dünya yüzeyindeki bir nesnenin ağırlığı, Newton'un ikinci hareket yasası veya F = m(a) (kuvvet = kütle × ivme) tarafından verilen, o nesne üzerindeki aşağı doğru kuvvettir. Yerçekimi ivmesi toplam yerçekimi ivmesine katkıda bulunur, ancak Dünya'nın dönüşü gibi diğer faktörler de katkıda bulunur ve bu nedenle nesnenin ağırlığını etkiler. Yerçekimi normalde Ay ve Güneş'in yerçekimini içermez, bunlar gelgit etkileri açısından hesaba katılır. ⓘ

Büyüklükteki değişim

Tek tip kütle yoğunluğuna sahip ya da yoğunluğu yalnızca merkezden uzaklığa göre değişen (küresel simetri) dönmeyen mükemmel bir küre, yüzeyindeki tüm noktalarda tek tip büyüklükte bir yerçekimi alanı üretecektir. Dünya dönmektedir ve aynı zamanda küresel simetrik değildir; daha ziyade, kutuplarda hafifçe düzleşirken Ekvator'da şişkinleşir: bir oblate sferoid. Dolayısıyla yüzeyindeki yerçekimi büyüklüğünde hafif sapmalar vardır. ⓘ

Dünya yüzeyindeki yerçekimi Peru'daki Nevado Huascarán dağında 9.7639 m/s² ile Kuzey Buz Denizi yüzeyinde 9.8337 m/s² arasında yaklaşık %0.7 oranında değişmektedir. Büyük şehirlerde ise Kuala Lumpur, Mexico City ve Singapur'da 9.7806 ile Oslo ve Helsinki'de 9.825 arasında değişmektedir. ⓘ

Geleneksel değer

1901 yılında üçüncü Ağırlıklar ve Ölçüler Genel Konferansı, Dünya yüzeyi için standart bir yerçekimi ivmesi tanımladı: gn = 9.80665 m/s². Bu değer, 1888 yılında Paris yakınlarındaki Pavillon de Breteuil'de yapılan ölçümlere dayanmakta olup, deniz seviyesinde 45° enleme dönüştürmek için teorik bir düzeltme uygulanmıştır. Dolayısıyla bu tanım belirli bir yerin değeri ya da dikkatlice çalışılmış bir ortalama değil, daha iyi bir gerçek yerel değer bilinmiyorsa ya da önemli değilse kullanılacak bir değer için bir anlaşmadır. Aynı zamanda kilogram kuvveti ve pound kuvveti birimlerini tanımlamak için de kullanılır. ⓘ

Dünya'nın ortalama yarıçapı (6,371 kilometre (3,959 mil)), yerçekimi sabitinin deneysel olarak belirlenen değeri ve 5.9722 ×10²⁴ kg'lık Dünya kütlesi kullanılarak Dünya yüzeyindeki yerçekiminin hesaplanması, 9.80665 m/s2'lik standart yerçekiminden biraz daha büyük olan 9.8²03 m/s²'lik bir ivme verir. Standart yerçekimi değeri, 6.375,4 kilometre (3.961,5 mil) yarıçapında Dünya'daki yerçekimine karşılık gelir. ⓘ

Enlem

Antarktika kıtası etrafında Dünya'nın yerçekimi farklılıkları. ⓘ

Dünya'nın yüzeyi dönmektedir, bu nedenle eylemsiz bir referans çerçevesi değildir. Ekvator'a yakın enlemlerde, Dünya'nın dönüşü tarafından üretilen dışa doğru merkezkaç kuvveti kutup enlemlerine göre daha büyüktür. Bu, Dünya'nın yerçekimini küçük bir dereceye kadar - Ekvator'da maksimum %0,3'e kadar - etkisiz hale getirir ve düşen nesnelerin görünürdeki aşağı doğru ivmesini azaltır. ⓘ

Farklı enlemlerdeki yerçekimi farklılığının ikinci önemli nedeni, Dünya'nın ekvatoral çıkıntısının (kendisi de dönüşten kaynaklanan merkezkaç kuvvetinden kaynaklanır) Ekvator'daki nesnelerin kutuplardaki nesnelere göre gezegenin merkezinden daha uzakta olmasına neden olmasıdır. İki cisim (Dünya ve tartılan cisim) arasındaki yerçekiminden kaynaklanan kuvvet, aralarındaki mesafenin karesiyle ters orantılı olarak değiştiğinden, Ekvator'daki bir cisim kutuptaki bir cisme göre daha zayıf bir yerçekimine maruz kalır. ⓘ

Ekvator çıkıntısı ve dönmeye bağlı yüzey merkezkaç kuvvetinin etkileri bir araya geldiğinde, deniz seviyesindeki yerçekiminin Ekvator'da yaklaşık 9,780 m/s²'den kutuplarda yaklaşık 9,832 m/s²'ye yükseldiği, dolayısıyla bir nesnenin kutuplarda Ekvator'dakinden yaklaşık %0,5 daha ağır olacağı anlamına gelir. ⓘ

Yükseklik

Grafik, bir nesnenin yüzey üzerindeki yüksekliğine göre yerçekimindeki değişimi göstermektedir ⓘ

Dünya yüzeyinden yükseldikçe yerçekimi azalır çünkü daha yüksek irtifa Dünya'nın merkezinden daha fazla mesafe anlamına gelir. Diğer her şey eşit olduğunda, deniz seviyesinden 9.000 metre (30.000 ft) yüksekliğe çıkmak ağırlıkta yaklaşık %0,29'luk bir azalmaya neden olur. (Görünür ağırlığı etkileyen ek bir faktör de yükseklikte hava yoğunluğunun azalmasıdır, bu da bir nesnenin kaldırma kuvvetini azaltır. Bu durum, 9.000 metre yükseklikteki bir kişinin görünür ağırlığını yaklaşık %0,08 oranında artıracaktır) ⓘ

Yörüngedeki astronotların Dünya'nın yerçekiminden kaçacak kadar yükseğe uçtukları için ağırlıksız oldukları yaygın bir yanılgıdır. Aslında, ISS'nin tipik bir yörüngesine eşdeğer olan 400 kilometre (250 mil) yükseklikte, yerçekimi hala Dünya yüzeyindekinden yaklaşık %90 daha güçlüdür. Ağırlıksızlık aslında yörüngedeki nesneler serbest düşüşte olduğu için meydana gelir. ⓘ

Yer yüksekliğinin etkisi zeminin yoğunluğuna bağlıdır (bkz. Döşeme düzeltmesi bölümü). Deniz seviyesinden 9.100 m (30.000 ft) yükseklikte dağların üzerinde uçan bir kişi, aynı yükseklikte fakat deniz üzerinde uçan bir kişiye göre daha fazla yerçekimi hissedecektir. Ancak, Dünya'nın yüzeyinde duran bir kişi, yükseklik daha fazla olduğunda daha az yerçekimi hisseder. ⓘ

Aşağıdaki formül Dünya'nın yerçekiminin yükseklikle değişimini yaklaşık olarak vermektedir:

$g_{h}=g_{0}\left({\frac {R_{\mathrm {e} }}{R_{\mathrm {e} }+h}}\right)^{2}$ ⓘ

Nerede

• gh deniz seviyesinden h yüksekliğindeki yerçekimi ivmesidir.
• R_e, Dünya'nın ortalama yarıçapıdır.
• g₀ standart yerçekimi ivmesidir. ⓘ

Formül, Dünya'yı radyal simetrik kütle dağılımına sahip mükemmel bir küre olarak ele alır; daha doğru bir matematiksel işlem aşağıda tartışılmaktadır. ⓘ

Derinlik

Ön Referans Dünya Modeline (PREM) göre Dünya'nın radyal yoğunluk dağılımı. ⓘ

Ön Referans Dünya Modeline (PREM) göre dünyanın yerçekimi. Karşılaştırma için küresel simetrik bir Dünya için iki model dahil edilmiştir. Koyu yeşil düz çizgi, Dünya'nın ortalama yoğunluğuna eşit sabit bir yoğunluk içindir. Açık yeşil eğri çizgi, merkezden yüzeye doğrusal olarak azalan bir yoğunluk içindir. Merkezdeki yoğunluk, PREM'deki ile aynıdır, ancak yüzey yoğunluğu, kürenin kütlesi gerçek Dünya'nın kütlesine eşit olacak şekilde seçilir. ⓘ

Dünya'nın merkezinden r mesafedeki yaklaşık bir yerçekimi değeri, Dünya'nın yoğunluğunun küresel olarak simetrik olduğu varsayılarak elde edilebilir. Yerçekimi, yalnızca r yarıçaplı kürenin içindeki kütleye bağlıdır. Yerçekiminin ters kare yasasından dışarıdan gelen tüm katkılar birbirini götürür. Diğer bir sonuç da, yerçekiminin, tüm kütlenin merkezde yoğunlaşması gibi aynı olmasıdır. Bu nedenle, bu yarıçaptaki yerçekimi ivmesi

$g(r)=-\ frac{GM(r)}{r^{2}}.$

burada G yerçekimi sabiti ve M ( r ), r yarıçapı içindeki toplam kütledir. Dünyanın sabit bir yoğunluğu ρ olsaydı, kütle M ( r ) = (4/3) πρr 'olurdu ' ³ ve yer çekiminin derinliğe bağımlılığı

$g(r)=\ frac{4\ pi}{3}G\ rhor.$

d derinliğindeki yerçekimi g ' şu şekilde verilir: g '=' 'g' '(1 -' 'd' '/' 'R' ') burada g yerçekimine bağlı ivmedir Dünya'nın yüzeyinde, d derinliktir ve R Dünya nın yarıçapıdır. Yoğunluk, merkezdeki yoğunluk ρ ₀ 'den ' 'ρ' ' _{1 </ sub >} yüzeyde, ardından ρ ( r ) = ρ ₀ - ( ρ < alt> 0 - ρ ₁ ) r / r _e ve bağımlılık

$g(r)=\ frac{4\ pi}{3}G\ rho_{0}r-\ piG\ left(\ rho_{0}-\ rho_{1}\ right)\ frac{r^{2}}{r_{\ mathrm{e}}}.$ ⓘ

Sismik seyahat sürelerinden (Adams – Williamson denklemi çıkarılan) yoğunluk ve yerçekiminin gerçek derinlik bağımlılığı aşağıdaki grafiklerde gösterilmektedir. ⓘ

Yerel topografya ve jeoloji

Topografyadaki (dağların varlığı gibi), jeolojideki (çevredeki kayaların yoğunluğu gibi) ve daha derin tektonik yapıdaki yerel farklılıklar, Dünya'nın yerçekimi alanında yerçekimi anomalileri olarak bilinen yerel ve bölgesel farklılıklara neden olur. Bu anomalilerin bazıları çok geniş kapsamlı olabilir, deniz seviyesinde şişkinliklere yol açabilir ve sarkaçlı saatleri senkronizasyondan çıkarabilir. ⓘ

Bu anomalilerin incelenmesi yerçekimsel jeofiziğin temelini oluşturur. Dalgalanmalar son derece hassas gravimetrelerle ölçülür, topografyanın ve diğer bilinen faktörlerin etkisi çıkarılır ve elde edilen verilerden sonuçlar çıkarılır. Bu tür teknikler artık petrol ve maden yataklarını bulmak için araştırmacılar tarafından kullanılmaktadır. Daha yoğun kayalar (genellikle mineral cevherleri içeren) Dünya yüzeyinde normalden daha yüksek yerel yerçekimi alanlarına neden olur. Daha az yoğun tortul kayaçlar ise tam tersine neden olur. ⓘ

Son volkanik faaliyetlerin ve sırt yayılmalarının bir haritası. NASA GRACE'in yerçekimini teorik yerçekiminden daha güçlü olarak ölçtüğü alanlar, volkanik aktivitenin ve sırt yayılmasının konumları ile güçlü bir korelasyona sahiptir. ⓘ

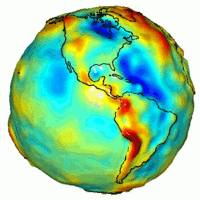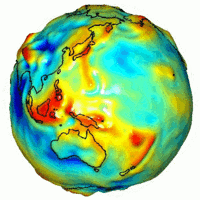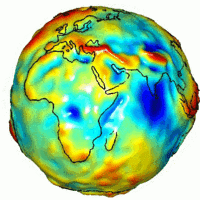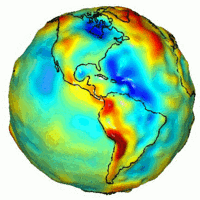
NASA GRACE'den elde edilen yerçekimi türetme haritası ile yakın zamandaki volkanik faaliyet, sırt yayılması ve volkanların konumları arasında güçlü bir korelasyon vardır. Bu bölgeler teorik tahminlerden daha güçlü bir yerçekimine sahiptir. ⓘ

Diğer faktörler

Havada veya suda nesneler, görünen yerçekimi kuvvetini azaltan (bir nesnenin ağırlığı ile ölçüldüğü üzere) destekleyici bir kaldırma kuvveti kuvvetine maruz kalır. Etkinin büyüklüğü sırasıyla hava yoğunluğuna (ve dolayısıyla hava basıncına) veya su yoğunluğuna bağlıdır; ayrıntılar için Görünen ağırlık bölümüne bakın. ⓘ

Ay ve Güneş 'in yerçekimi etkileri (aynı zamanda gelgitler' lerin nedeni), göreli konumlarına bağlı olarak, Dünya'nın yerçekiminin görünen gücü üzerinde çok küçük bir etkiye sahiptir; tipik varyasyonlar bir gün boyunca 2 µm / s ² (0.2 mGal) şeklindedir. ⓘ

Yön

Bir çekül yerel dikey yönü belirler ⓘ

Yerçekimi ivmesi, büyüklüğe ek olarak yönü de olan vektörel bir niceliktir. Küresel olarak simetrik bir Dünya'da yerçekimi doğrudan kürenin merkezine doğru olacaktır. Dünya'nın şekli biraz daha düz olduğundan, yerçekiminin yönünde önemli sapmalar vardır: esasen jeodezik enlem ile jeosentrik enlem arasındaki fark. Dikey sapma olarak adlandırılan daha küçük sapmalar, dağlar gibi yerel kütle anomalilerinden kaynaklanır. ⓘ

Dünya çapında karşılaştırmalı değerler

Dünyanın çeşitli şehirlerinde yerçekiminin gücünü hesaplamak için araçlar mevcuttur. Enlemin etkisi, yüksek enlemli şehirlerdeki yerçekimi ile açıkça görülebilir: Anchorage (9,826 m/s²), Helsinki (9,825 m/s²), ekvatora yakın şehirlerden yaklaşık %0,5 daha büyüktür: Kuala Lumpur (9.776 m/s²). Yüksekliğin etkisi Mexico City'de (9.776 m/s²; yükseklik 2,240 metre (7,350 ft)) ve Denver (9.798 m/s²; 1,616 metre (5,302 ft)) ile Washington, D.C. (9.801 m/s²; 30 metre (98 ft)) karşılaştırılarak görülebilir, her ikisi de 39° N'ye yakındır. Ölçülen değerler T.M. Yarwood ve F. Castle tarafından hazırlanan Physical and Mathematical Tables, Macmillan, revised edition 1970'den elde edilebilir. ⓘ

Çeşitli şehirlerde yerçekimine bağlı ivme ⓘ

Konum	m/s2	ft/s2		Konum	m/s2	ft/s2		Konum	m/s2	ft/s2
Amsterdam	9.817	32.21		Cakarta	9.777	32.08		Ottawa	9.806	32.17
Anchorage	9.826	32.24		Kandy	9.775	32.07		Paris	9.809	32.18
Atina	9.800	32.15		Kolkata	9.785	32.10		Perth	9.794	32.13
Auckland	9.799	32.15		Kuala Lumpur	9.776	32.07		Rio de Janeiro	9.788	32.11
Bangkok	9.780	32.09		Kuveyt Şehri	9.792	32.13		Roma	9.803	32.16
Birmingham	9.817	32.21		Lizbon	9.801	32.16		Seattle	9.811	32.19
Brüksel	9.815	32.20		Londra	9.816	32.20		Singapur	9.776	32.07
Buenos Aires	9.797	32.14		Los Angeles	9.796	32.14		Üsküp	9.804	32.17
Cape Town	9.796	32.14		Madrid	9.800	32.15		Stockholm	9.818	32.21
Chicago	9.804	32.17		Manchester	9.818	32.21		Sidney	9.797	32.14
Kopenhag	9.821	32.22		Manila	9.780	32.09		Taipei	9.790	32.12
Denver	9.798	32.15		Melbourne	9.800	32.15		Tokyo	9.798	32.15
Frankfurt	9.814	32.20		Meksika Şehri	9.776	32.07		Toronto	9.807	32.18
Havana	9.786	32.11		Montréal	9.809	32.18		Vancouver	9.809	32.18
Helsinki	9.825	32.23		New York Şehri	9.802	32.16		Washington, D.C.	9.801	32.16
Hong Kong	9.785	32.10		Lefkoşa	9.797	32.14		Wellington	9.803	32.16
İstanbul	9.808	32.18		Oslo	9.825	32.23		Zürih	9.807	32.18

Matematiksel modeller

Arazi deniz seviyesindeyse, 1980 Jeodezik Referans Sistemi için tahmin yapabiliriz, $g\{\phi \}$, enlemdeki ivme $\phi$:

${\begin{aligned}g\{\phi \}&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1+0.0053024\,\sin ^{2}\phi -0.0000058\,\sin ^{2}2\phi \right),\\&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1+0.0052792\,\sin ^{2}\phi +0.0000232\,\sin ^{4}\phi \right),\\&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1.0053024-0.0053256\,\cos ^{2}\phi +0.0000232\,\cos ^{4}\phi \right),\\&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1.0026454-0.0026512\,\cos 2\phi +0.0000058\,\cos ^{2}2\phi \right)\end{aligned}}$ ⓘ

Bu, 1967 Uluslararası Yerçekimi Formülü, 1967 Jeodezik Referans Sistemi Formülü, Helmert'in denklemi veya Clairaut'un formülüdür. ⓘ

Enlemin bir fonksiyonu olarak g için alternatif bir formül WGS (Dünya Jeodezik Sistemi) 84 Elipsoidal Yerçekimi Formülüdür:

$g\{\phi \}=\mathbb {G} _{e}\left[{\frac {1+k\sin ^{2}\phi }{\sqrt {1-e^{2}\sin ^{2}\phi }}}\right],\,\!$

burada, ⓘ

• $a,\,b$ sırasıyla ekvatoral ve kutupsal yarı eksenlerdir;
• $e^{2}=1-(b/a)^{2}$ sferoidin eksantrikliğinin karesidir;
• $\mathbb {G} _{e},\,\mathbb {G} _{p}\,$ sırasıyla ekvator ve kutuplarda tanımlanan yerçekimidir;
• $k={\frac {b\,\mathbb {G} _{p}-a\,\mathbb {G} _{e}}{a\,\mathbb {G} _{e}}}$ (formül sabiti); ⓘ

o zaman, burada $\mathbb {G} _{p}=9.8321849378\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}$,

$g\{\phi \}=9.7803253359\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\left[{\frac {1+0.001931852652\,\sin ^{2}\phi }{\sqrt {1-0.0066943799901\,\sin ^{2}\phi }}}\right]$. ⓘ

dünyanın yarı eksenlerinin olduğu yer:

$a=6378137.0\,\,{\mbox{m}}$

$b=6356752.314245\,\,{\mbox{m}}$ ⓘ

WGS-84 formülü ile Helmert denklemi arasındaki fark 0,68 μm-s-2'den azdır. ⓘ

Yerçekimi anomalilerini elde etmek için daha fazla indirgeme uygulanır (bkz: Yerçekimi anomalisi#Hesaplama). ⓘ

Evrensel çekim yasasından g'nin tahmin edilmesi

Evrensel çekim yasasına göre, Dünya'nın çekim kuvvetinin etki ettiği bir cisim üzerindeki kuvvet şu şekilde verilir

$F=G{\frac {m_{1}m_{2}}{r^{2}}}=(G{\frac {M_{\oplus }}{r^{2}}})m$ ⓘ

Burada r, Dünya'nın merkezi ile cisim arasındaki mesafedir (aşağıya bakınız) ve burada $M_{\oplus }$ Dünya'nın kütlesi ve m cismin kütlesi olmak üzere. ⓘ

Ek olarak, Newton'un ikinci yasası, F = ma, burada m kütle ve a ivmedir, burada bize şunu söyler

$F=mg$ ⓘ

İki formül karşılaştırıldığında şu görülür:

$g=G{\frac {M_{\oplus }}{r^{2}}}$ ⓘ

Deniz seviyesinde yerçekiminden kaynaklanan ivmeyi bulmak için, yerçekimi sabiti G, Dünya'nın kütlesi (kilogram cinsinden) m₁ ve Dünya'nın yarıçapı (metre cinsinden) r değerlerini yerine koyarak g değerini elde edin:

$g=G{\frac {M_{\oplus }}{r^{2}}}=6.67\cdot 10^{-11}{m}^{3}{kg}^{-1}{s}^{-2}\times {\frac {6\times 10^{24}{kg}}{(6.4\times 10^{6}{m})^{2}}}=9.77{m}.{s}^{-2}$ ⓘ

Bu formülün işe yaramasının tek nedeni, düzgün küresel bir cismin yüzeyinde veya üzerinde ölçülen yerçekiminin, tüm kütlesi merkezindeki bir noktada yoğunlaşmış gibi aynı olduğu matematiksel gerçeğidir. Bu, r için Dünya'nın yarıçapını kullanmamızı sağlayan şeydir. ⓘ

Elde edilen değer, g'nin ölçülen değeriyle yaklaşık olarak uyuşmaktadır. Aradaki fark, yukarıda "Varyasyonlar" başlığı altında bahsedilen çeşitli faktörlere bağlanabilir:

• Dünya homojen değildir
• Dünya mükemmel bir küre değildir ve yarıçapı için ortalama bir değer kullanılmalıdır
• Hesaplanan bu g değeri sadece gerçek yerçekimini içerir. Dünya'nın dönüşü nedeniyle yerçekiminin azalması olarak algıladığımız kısıtlama kuvvetinin azalmasını ve yerçekiminin bir kısmının merkezkaç kuvveti tarafından etkisiz hale getirilmesini içermez.

Bu hesaplamada kullanılan r ve m₁ değerlerinde önemli belirsizlikler vardır ve G değerinin kesin olarak ölçülmesi de oldukça zordur. ⓘ

Eğer G, g ve r biliniyorsa, tersine bir hesaplama Dünya'nın kütlesinin tahmin edilmesini sağlayacaktır. Bu yöntem Henry Cavendish tarafından kullanılmıştır. ⓘ

Ölçüm

Dünya'nın yerçekiminin ölçülmesine gravimetri denir. ⓘ