Algoritma


Matematik ve bilgisayar biliminde bir algoritma (/ˈælɡərɪðəm/ (![]() dinle)), tipik olarak belirli bir problem sınıfını çözmek veya bir hesaplama gerçekleştirmek için kullanılan sonlu bir titiz talimatlar dizisidir. Algoritmalar, hesaplamaları ve veri işlemeyi gerçekleştirmek için spesifikasyonlar olarak kullanılır. Algoritmalar, yapay zekadan yararlanarak otomatik çıkarımlar yapabilir (otomatik muhakeme olarak adlandırılır) ve kod yürütmesini çeşitli yollardan yönlendirmek için matematiksel ve mantıksal testler kullanabilir (otomatik karar verme olarak adlandırılır). İnsan özelliklerinin metaforik yollarla makinelerin tanımlayıcıları olarak kullanılması, Alan Turing tarafından "hafıza", "arama" ve "uyarıcı" gibi terimlerle zaten uygulanmıştı. ⓘ
dinle)), tipik olarak belirli bir problem sınıfını çözmek veya bir hesaplama gerçekleştirmek için kullanılan sonlu bir titiz talimatlar dizisidir. Algoritmalar, hesaplamaları ve veri işlemeyi gerçekleştirmek için spesifikasyonlar olarak kullanılır. Algoritmalar, yapay zekadan yararlanarak otomatik çıkarımlar yapabilir (otomatik muhakeme olarak adlandırılır) ve kod yürütmesini çeşitli yollardan yönlendirmek için matematiksel ve mantıksal testler kullanabilir (otomatik karar verme olarak adlandırılır). İnsan özelliklerinin metaforik yollarla makinelerin tanımlayıcıları olarak kullanılması, Alan Turing tarafından "hafıza", "arama" ve "uyarıcı" gibi terimlerle zaten uygulanmıştı. ⓘ
Buna karşılık, sezgisel bir yaklaşım, özellikle iyi tanımlanmış doğru veya optimal bir sonucun olmadığı problem alanlarında, tam olarak belirlenmemiş veya doğru veya optimal sonuçları garanti etmeyebilen problem çözme yaklaşımıdır. ⓘ
Etkili bir yöntem olarak bir algoritma, sonlu miktarda alan ve zaman içinde ve bir fonksiyonun hesaplanması için iyi tanımlanmış bir resmi dilde ifade edilebilir. Bir başlangıç durumundan ve başlangıç girdisinden (belki de boş) başlayarak, talimatlar, yürütüldüğünde, sonlu sayıda iyi tanımlanmış ardışık durum boyunca ilerleyen, sonunda "çıktı" üreten ve nihai bir bitiş durumunda sona eren bir hesaplamayı tanımlar. Bir durumdan diğerine geçiş mutlaka deterministik olmak zorunda değildir; rastgele algoritmalar olarak bilinen bazı algoritmalar rastgele girdi içerir. ⓘ
İlk algoritma, el-Hârizmî tarafından "Hisab el-cebir ve el-mukabala" kitabında sunulmuştur. Algoritma sözcüğü de el-Hârizmî'nin isminin Avrupalılarca telaffuzundan doğmuştur. ⓘ
Tarihçe
Algoritma kavramı antik çağlardan beri var olmuştur. Bölme algoritması gibi aritmetik algoritmalar, MÖ 2500 civarında eski Babilli matematikçiler ve MÖ 1550 civarında Mısırlı matematikçiler tarafından kullanılmıştır. Yunan matematikçiler daha sonra algoritmaları MÖ 240 yılında asal sayıları bulmak için Eratosthenes'in eleğinde ve iki sayının en büyük ortak bölenini bulmak için Öklid algoritmasında kullanmışlardır. El Kindi gibi Arap matematikçiler 9. yüzyılda frekans analizine dayanan şifre kırma algoritmalarını kullanmışlardır. ⓘ
Algoritma kelimesi, nisbesi (Harezmli olduğunu belirten) Algoritmi (Araplaştırılmış Farsça الخوارزمی c. 780-850) olarak Latinceleştirilen 9. yüzyıl Fars matematikçisi Muḥammad ibn Mūsā al-Khwārizmī'nin adından türetilmiştir. Muhammed ibn Mûsâ el-Hârizmî, matematikçi, astronom, coğrafyacı ve Bağdat'taki Bilgelik Evi'nin âlimiydi ve adı, Büyük İran'ın bir parçası olan ve bugün Özbekistan'da bulunan bir bölge olan 'Harezm'in yerlisi' anlamına geliyordu. Harezmi, yaklaşık 825 yılında Hindu-Arap rakam sistemi üzerine Arapça bir risale yazmış ve bu risale 12. yüzyılda Latinceye çevrilmiştir. El yazması, Dixit Algorizmi ('Thus spake Al-Khwarizmi') ifadesiyle başlar; burada "Algorizmi", çevirmenin Harizmi'nin adını Latinceleştirmesidir. Harezmi, Orta Çağ'ın sonlarında Avrupa'da en çok okunan matematikçiydi, özellikle de bir başka kitabı olan Cebir aracılığıyla. Geç Ortaçağ Latincesinde, isminin bozulmuş hali olan algorismus, İngilizce 'algorism', basitçe "ondalık sayı sistemi" anlamına geliyordu. 15. yüzyılda, Yunanca ἀριθμός (arithmos), 'sayı' (bkz. 'aritmetik') kelimesinin etkisi altında, Latince kelime algoritmus olarak değiştirildi ve buna karşılık gelen İngilizce 'algoritma' terimi ilk olarak 17. yüzyılda görüldü; modern anlamı ise 19. yüzyılda ortaya çıktı. ⓘ
Hint matematiği ağırlıklı olarak algoritmiktir. Hint matematik geleneğini temsil eden algoritmalar, antik Śulbasūtrās'tan Kerala Okulu'nun ortaçağ metinlerine kadar uzanır. ⓘ
İngilizce'de algoritma kelimesi ilk olarak yaklaşık 1230'da ve daha sonra 1391'de Chaucer tarafından kullanılmıştır. İngilizce Fransızca terimi benimsemiştir, ancak "algoritma" modern İngilizcede sahip olduğu anlamı 19. yüzyılın sonlarına kadar kazanmamıştır. ⓘ
Kelimenin bir diğer erken kullanımı 1240 yılına ait olup Alexandre de Villedieu tarafından kaleme alınan Carmen de Algorismo başlıklı bir el kitabında yer almaktadır. Şöyle başlamaktadır:
Haec algorismus ars praesens dicitur, in qua / Talibus Indorum fruimur bis quinque figuris.
Bu da şu anlama gelir:
Algorizm, şu anda sayıları iki kere beş olan Hint rakamlarını kullandığımız sanattır. ⓘ
Şiir birkaç yüz satır uzunluğundadır ve yeni tarz Hint zarları (Tali Indorum) ya da Hindu rakamları ile hesaplama sanatını özetlemektedir. ⓘ
Modern algoritma kavramının kısmi biçimlendirilmesi, 1928 yılında David Hilbert tarafından ortaya atılan Entscheidungsproblem'i (karar problemi) çözme girişimleriyle başlamıştır. Daha sonraki formalizasyonlar "etkin hesaplanabilirlik" veya "etkin yöntem" tanımlama girişimleri olarak çerçevelenmiştir. Bu biçimlendirmeler arasında 1930, 1934 ve 1935 tarihli Gödel-Herbrand-Kleene özyinelemeli fonksiyonları, Alonzo Church'ün 1936 tarihli lambda hesabı, Emil Post'un 1936 tarihli Formülasyon 1'i ve Alan Turing'in 1936-37 ve 1939 tarihli Turing makineleri yer almaktadır. ⓘ
Resmi olmayan tanım
Gayri resmi bir tanım, "bir dizi işlemi kesin olarak tanımlayan kurallar dizisi" olabilir; bu, tüm bilgisayar programlarını (sayısal hesaplamalar yapmayan programlar dahil) ve (örneğin) öngörülen herhangi bir bürokratik prosedürü içerir ya da yemek kitabı tarifi. ⓘ
Genel olarak, bir program ancak eninde sonunda duruyorsa bir algoritmadır - sonsuz döngüler bazen arzu edilebilir olsa bile. ⓘ
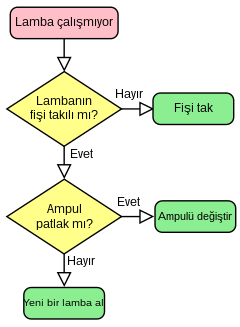
Bir algoritmanın prototipik örneği, iki tam sayının maksimum ortak bölenini belirlemek için kullanılan Öklid algoritmasıdır; bir örnek (başkaları da vardır) yukarıdaki akış şemasında ve daha sonraki bir bölümde örnek olarak açıklanmıştır. ⓘ
Boolos, Jeffrey & 1974, 1999, aşağıdaki alıntıda "algoritma" kelimesinin gayri resmi bir anlamını sunmaktadır:
Hiçbir insan yeterince hızlı, yeterince uzun ya da yeterince küçük † ( †"sınırsızca daha küçük ve daha küçük ... moleküller, atomlar, elektronlar üzerine yazmaya çalışıyor olurdunuz") yazamaz, sayılamayacak kadar sonsuz bir kümenin tüm üyelerinin isimlerini bir notasyonda birbiri ardına yazarak listeleyemez. Ancak insanlar, belirli sayılabilir sonsuz kümeler söz konusu olduğunda eşit derecede faydalı bir şey yapabilirler: Bu tür talimatlar, bir bilgisayar makinesi ya da semboller üzerinde yalnızca çok temel işlemler yapabilen bir insan tarafından takip edilebilecek bir biçimde, oldukça açık bir şekilde verilmelidir. ⓘ
"Sayılabilir sonsuz küme", elemanları tamsayılarla bire bir örtüştürülebilen kümedir. Dolayısıyla Boolos ve Jeffrey, bir algoritmanın keyfi bir "girdi" tamsayısından ya da teoride keyfi olarak büyük olabilen tamsayılardan çıktı tamsayıları "yaratan" bir süreç için talimatlar anlamına geldiğini söylemektedir. Örneğin, bir algoritma y = m + n gibi cebirsel bir denklem olabilir (yani, bir y çıktısı üreten iki keyfi "girdi değişkeni" m ve n), ancak çeşitli yazarların kavramı tanımlama girişimleri, kelimenin bundan çok daha fazlasını, (toplama örneği için) mertebesinde bir şeyi ima ettiğini göstermektedir:
- "Bilgisayarın" (makine veya insan, gerekli dahili bilgi ve yeteneklerle donatılmış) m ve n giriş tamsayılarını/sembollerini, + ve = ... sembollerini bulmak, çözmek ve ardından işlemek ve "makul" bir sürede, belirli bir yerde ve belirli bir formatta y tamsayı çıktısını "etkin" bir şekilde üretmek için "hareketlerini" belirleyen hızlı, verimli, "iyi" bir süreç için ("bilgisayar" tarafından anlaşılan bir dilde) kesin talimatlar. ⓘ
Algoritma kavramı aynı zamanda karar verilebilirlik kavramını tanımlamak için de kullanılır; bu kavram, biçimsel sistemlerin küçük bir aksiyomlar ve kurallar kümesinden başlayarak nasıl ortaya çıktığını açıklamak için merkezi bir öneme sahiptir. Mantıkta, bir algoritmanın tamamlanması için gereken zaman ölçülemez, çünkü görünüşe göre alışılmış fiziksel boyutla ilgili değildir. Devam eden çalışmaları karakterize eden bu tür belirsizlikler, terimin hem somut (bir anlamda) hem de soyut kullanımına uygun bir algoritma tanımının mevcut olmamasından kaynaklanmaktadır. ⓘ
Çoğu algoritmanın bilgisayar programları olarak uygulanması amaçlanmaktadır. Ancak algoritmalar, biyolojik bir sinir ağında (örneğin, aritmetik uygulayan insan beyni veya yiyecek arayan bir böcek), bir elektrik devresinde veya mekanik bir cihazda olduğu gibi başka yollarla da uygulanmaktadır. ⓘ
Biçimselleştirme
Algoritmalar, bilgisayarların verileri işleme biçimi için çok önemlidir. Birçok bilgisayar programı, çalışanların maaş çeklerini hesaplamak veya öğrencilerin karnelerini basmak gibi belirli bir görevi yerine getirmek için bir bilgisayarın belirli bir sırayla gerçekleştirmesi gereken belirli talimatları detaylandıran algoritmalar içerir. Dolayısıyla bir algoritma, Turing-tam bir sistem tarafından simüle edilebilen herhangi bir işlem dizisi olarak düşünülebilir. Bu tezi savunan yazarlar arasında Minsky (1967), Savage (1987) ve Gurevich (2000) bulunmaktadır:
Minsky: "Ancak Turing ile birlikte ... "doğal olarak" etkin olarak adlandırılabilecek herhangi bir prosedürün aslında (basit) bir makine tarafından gerçekleştirilebileceğini de iddia edeceğiz. Bu aşırı görünse de, ... lehine olan argümanları çürütmek zordur". ⓘ Gurevich: "... Turing'in tezi lehindeki gayri resmi argümanı daha güçlü bir tezi haklı çıkarmaktadır: her algoritma bir Turing makinesi tarafından simüle edilebilir ... Savage'a [1987] göre, bir algoritma bir Turing makinesi tarafından tanımlanan bir hesaplama sürecidir".
Turing makineleri sonlanmayan hesaplama süreçlerini tanımlayabilir. Algoritmaların gayri resmi tanımları genellikle algoritmanın her zaman sonlanmasını gerektirir. Bu gereklilik, hesaplanabilirlik teorisinin durma problemi olarak bilinen önemli bir teoremi nedeniyle, resmi bir prosedürün bir algoritma olup olmadığına karar verme görevini genel durumda imkansız hale getirir. ⓘ
Tipik olarak, bir algoritma bilgi işleme ile ilişkilendirildiğinde, veriler bir giriş kaynağından okunabilir, bir çıkış cihazına yazılabilir ve daha sonraki işlemler için saklanabilir. Saklanan veriler, algoritmayı gerçekleştiren varlığın iç durumunun bir parçası olarak kabul edilir. Uygulamada, durum bir veya daha fazla veri yapısında saklanır. ⓘ
Bu hesaplama süreçlerinden bazıları için algoritma titizlikle tanımlanmalıdır: ortaya çıkabilecek tüm olası durumlarda uygulanacak şekilde belirtilmelidir. Bu, herhangi bir koşullu adımın sistematik olarak, durum bazında ele alınması gerektiği anlamına gelir; her durum için kriterler açık (ve hesaplanabilir) olmalıdır. ⓘ
Bir algoritma kesin adımların kesin bir listesi olduğundan, hesaplama sırası algoritmanın işleyişi için her zaman çok önemlidir. Talimatların genellikle açık bir şekilde listelendiği varsayılır ve "yukarıdan" başlayıp "aşağıya" inecek şekilde tanımlanır - bu fikir daha resmi olarak kontrol akışı ile tanımlanır. ⓘ
Şimdiye kadar, bir algoritmanın biçimlendirilmesine ilişkin tartışma, zorunlu programlamanın öncüllerini varsaymıştır. Bu, bir görevi ayrık, "mekanik" yollarla tanımlamaya çalışan en yaygın anlayıştır. Bu biçimlendirilmiş algoritma anlayışına özgü olan, bir değişkenin değerini belirleyen atama işlemidir. Bir karalama defteri olarak "bellek" sezgisinden türemiştir. Böyle bir atama örneği aşağıda bulunabilir. ⓘ
Bir algoritmayı neyin oluşturduğuna dair bazı alternatif kavramlar için işlevsel programlama ve mantıksal programlamaya bakınız. ⓘ
Algoritmaları ifade etme
Algoritmalar, doğal diller, sözde kod, akış şemaları, drakon şemaları, programlama dilleri veya kontrol tabloları (yorumlayıcılar tarafından işlenen) dahil olmak üzere birçok gösterim türünde ifade edilebilir. Algoritmaların doğal dil ifadeleri ayrıntılı ve muğlak olma eğilimindedir ve karmaşık veya teknik algoritmalar için nadiren kullanılır. Sözde kod, akış şemaları, drakon şemaları ve kontrol tabloları, doğal dile dayalı ifadelerde yaygın olan belirsizliklerin çoğundan kaçınan algoritmaları ifade etmenin yapılandırılmış yollarıdır. Programlama dilleri öncelikle algoritmaları bir bilgisayar tarafından yürütülebilecek bir biçimde ifade etmek için tasarlanmıştır, ancak genellikle algoritmaları tanımlamanın veya belgelemenin bir yolu olarak da kullanılır. ⓘ
Çok çeşitli gösterimler mümkündür ve belirli bir Turing makinesi programı bir dizi makine tablosu olarak (daha fazlası için sonlu durum makinesi, durum geçiş tablosu ve kontrol tablosuna bakınız), akış şemaları ve drakon şemaları olarak (daha fazlası için durum diyagramına bakınız) veya "dörtlü kümeler" adı verilen ilkel makine kodu veya montaj kodu olarak ifade edilebilir (daha fazlası için Turing makinesine bakınız). ⓘ
Algoritmaların gösterimleri, Turing makinesi tanımlamasının kabul edilen üç seviyesine aşağıdaki gibi sınıflandırılabilir:
- 1 Üst düzey tanımlama
- "...uygulama detaylarını göz ardı ederek bir algoritmayı tanımlamak için düzyazı. Bu seviyede, makinenin kasetini veya kafasını nasıl yönettiğinden bahsetmemize gerek yoktur."
- 2 Uygulama açıklaması
- "...Turing makinesinin kafasını kullanma şeklini ve verileri kasetinde saklama şeklini tanımlamak için kullanılan nesir. Bu seviyede, durumların veya geçiş fonksiyonlarının detaylarını vermiyoruz."
- 3 Biçimsel açıklama
- En ayrıntılı, "en düşük seviye", Turing makinesinin "durum tablosunu" verir. ⓘ
Her üç seviyede de açıklanan basit "Add m+n" algoritmasının bir örneği için bkz. ⓘ
Tasarım
Algoritma tasarımı, problem çözme ve mühendislik algoritmaları için bir yöntem veya matematiksel bir süreci ifade eder. Algoritmaların tasarımı, dinamik programlama ve böl ve yönet gibi yöneylem araştırmasının birçok çözüm teorisinin bir parçasıdır. Algoritma tasarımlarının tasarlanması ve uygulanmasına yönelik tekniklere algoritma tasarım kalıpları da denir ve bunlara şablon yöntem kalıbı ve dekoratör kalıbı gibi örnekler verilebilir. ⓘ
Algoritma tasarımının en önemli yönlerinden biri kaynak (çalışma zamanı, bellek kullanımı) verimliliğidir; big O notasyonu, örneğin bir algoritmanın girdisinin boyutu arttıkça çalışma zamanındaki büyümesini tanımlamak için kullanılır. ⓘ
Algoritmaların geliştirilmesindeki tipik adımlar:
- Problem tanımı
- Bir modelin geliştirilmesi
- Algoritmanın özellikleri
- Bir algoritma tasarlama
- Algoritmanın doğruluğunun kontrol edilmesi
- Algoritma analizi
- Algoritmanın uygulanması
- Program testi
- Dokümantasyon hazırlığı ⓘ
Bilgisayar algoritmaları


IF test THEN GOTO adım xxxelmas olarak gösterilmiştir), koşulsuz GOTO (dikdörtgen), çeşitli atama operatörleri (dikdörtgen) ve HALT (dikdörtgen). Bu yapıların atama bloklarının içine yerleĢtirilmesi karmaĢık diyagramlar oluĢturur (bkz. Tausworthe 1977:100, 114). ⓘ"Zarif" (kompakt) programlar, "iyi" (hızlı) programlar : "Basitlik ve zarafet" kavramı Knuth'ta gayri resmi olarak, Chaitin'de ise kesin olarak yer almaktadır:
- Knuth: " ... gevşek bir şekilde tanımlanmış estetik anlamda iyi algoritmalar istiyoruz. Bir kriter ... algoritmayı gerçekleştirmek için harcanan zamanın uzunluğudur .... Diğer kriterler ise algoritmanın bilgisayarlara uyarlanabilirliği, basitliği ve zarafeti vb." ⓘ
- Chaitin: " ... bir programın 'zarif' olması demek, yaptığı çıktıyı üretmek için mümkün olan en küçük program olması demektir" ⓘ
Chaitin tanımına şöyle başlar: "Bir programın 'zarif' olduğunu kanıtlayamayacağınızı göstereceğim" - böyle bir kanıt Halting problemini çözecektir (ibid). ⓘ
Algoritmaya karşı bir algoritma tarafından hesaplanabilen fonksiyon: Belirli bir fonksiyon için birden fazla algoritma mevcut olabilir. Bu, programcının kullanabileceği mevcut komut setini genişletmeden bile doğrudur. Rogers şu gözlemde bulunmaktadır: "Algoritma, yani prosedür kavramı ile algoritma tarafından hesaplanabilir fonksiyon, yani prosedür tarafından verilen eşleme kavramını birbirinden ayırmak önemlidir. Aynı fonksiyonun birkaç farklı algoritması olabilir". ⓘ
Ne yazık ki, iyilik (hız) ve zarafet (kompaktlık) arasında bir ödünleşme olabilir - zarif bir programın bir hesaplamayı tamamlaması, daha az zarif olana göre daha fazla adım gerektirebilir. Öklid'in algoritmasını kullanan bir örnek aşağıda yer almaktadır. ⓘ
Bilgisayarlar (ve hesaplayıcılar), hesaplama modelleri: Bir bilgisayar (ya da insan "hesaplayıcı") kısıtlı bir makine türüdür, talimatlarını körü körüne takip eden "ayrık deterministik mekanik bir cihazdır". Melzak ve Lambek'in ilkel modelleri bu kavramı dört unsura indirgemiştir: (i) ayrık, ayırt edilebilir konumlar, (ii) ayrık, ayırt edilemez sayaçlar (iii) bir aracı ve (iv) aracının kapasitesine göre etkili olan bir talimatlar listesi. ⓘ
Minsky, "Hesaplanabilirlik için Çok Basit Temeller" adlı eserinde Lambek'in "abaküs" modelinin daha uygun bir varyasyonunu tanımlamaktadır. Minsky'nin makinesi, koşullu bir IF-THEN GOTO veya koşulsuz bir GOTO program akışını sıra dışında değiştirmediği sürece beş (veya nasıl sayıldığına bağlı olarak altı) talimat boyunca sırayla ilerler. HALT'ın yanı sıra, Minsky'nin makinesi üç atama (değiştirme, ikame) işlemi içerir: ZERO (örneğin konumun içeriği 0 ile değiştirilir: L ← 0), SUCCESSOR (örneğin L ← L+1) ve DECREMENT (örneğin L ← L - 1). Bir programcı nadiren bu kadar sınırlı bir komut setiyle "kod" yazmalıdır. Ancak Minsky (Melzak ve Lambek'in yaptığı gibi) makinesinin yalnızca dört genel talimat türüyle Turing tamamlandığını göstermektedir: koşullu GOTO, koşulsuz GOTO, atama/değiştirme/değiştirme ve HALT. Bununla birlikte, birkaç farklı atama talimatı (örneğin bir Minsky makinesi için DECREMENT, INCREMENT ve ZERO/CLEAR/EMPTY) da Turing-tamlığı için gereklidir; bunların tam olarak belirtilmesi biraz tasarımcıya bağlıdır. Koşulsuz GOTO bir kolaylıktır; özel bir konumun sıfıra başlatılmasıyla oluşturulabilir, örneğin " Z ← 0 " komutu; bundan sonra IF Z=0 THEN GOTO xxx komutu koşulsuzdur. ⓘ
Bir algoritmanın simülasyonu: bilgisayar (computor) dili: Knuth okuyucuya "bir algoritmayı öğrenmenin en iyi yolu onu denemektir ... hemen kağıt kalemi alın ve bir örnek üzerinde çalışın" tavsiyesinde bulunur. Peki ya gerçek bir şeyin simülasyonu ya da uygulaması? Programcı algoritmayı simülatörün/bilgisayarın/bilgisayarcının etkin bir şekilde çalıştırabileceği bir dile çevirmelidir. Stone buna bir örnek veriyor: ikinci dereceden bir denklemin köklerini hesaplarken bilgisayarın karekökü nasıl alacağını bilmesi gerekir. Eğer bilmiyorsa, algoritmanın etkili olabilmesi için karekökü çıkarmak için bir dizi kural sağlaması gerekir. ⓘ
Bu, programcının hedef bilgi işlem aracına (bilgisayar/bilgisayar) göre etkili olan bir "dil" bilmesi gerektiği anlamına gelir. ⓘ
Peki simülasyon için hangi model kullanılmalıdır? Van Emde Boas, "karmaşıklık teorisini somut makineler yerine soyut makinelere dayandırsak bile, model seçimindeki keyfilik devam eder. İşte bu noktada simülasyon kavramı devreye girmektedir". Hız ölçülürken, komut seti önemlidir. Örneğin, Öklid'in algoritmasındaki kalanı hesaplayan alt program, programcının sadece çıkarma (veya daha kötüsü: sadece Minsky'nin "azaltma") yerine bir "modül" komutuna sahip olması durumunda çok daha hızlı çalışacaktır. ⓘ
Yapısal programlama, kanonik yapılar: Church-Turing tezine göre, herhangi bir algoritma Turing tamlığı olduğu bilinen bir model tarafından hesaplanabilir ve Minsky'nin gösterimlerine göre, Turing tamlığı yalnızca dört komut türü gerektirir - koşullu GOTO, koşulsuz GOTO, atama, HALT. Kemeny ve Kurtz, koşulsuz GOTO'ların ve koşullu IF-THEN GOTO'ların "disiplinsiz" kullanımının "spagetti kod" ile sonuçlanabileceğini, ancak bir programcının yalnızca bu talimatları kullanarak yapılandırılmış programlar yazabileceğini; öte yandan "yapılandırılmış bir dilde kötü yapılandırılmış programlar yazmanın da mümkün olduğunu ve çok zor olmadığını" gözlemlemektedir. Tausworthe üç Böhm-Jacopini kanonik yapısını genişletir: SEQUENCE, IF-THEN-ELSE ve WHILE-DO, iki tane daha ekler: DO-WHILE ve CASE. Yapılandırılmış bir programın ek bir faydası da matematiksel tümevarım kullanarak doğruluk kanıtlarına kendini ödünç vermesidir. ⓘ
Kanonik akış şeması sembolleri: Akış şeması adı verilen grafiksel yardımcı, bir algoritmayı (ve bir bilgisayar programını) tanımlamak ve belgelemek için bir yol sunar. Bir Minsky makinesinin program akışı gibi, bir akış şeması her zaman bir sayfanın en üstünden başlar ve aşağı doğru ilerler. Temel sembolleri sadece dört tanedir: program akışını gösteren yönlendirilmiş ok, dikdörtgen (SEQUENCE, GOTO), elmas (IF-THEN-ELSE) ve nokta (OR-tie). Böhm-Jacopini kanonik yapıları bu ilkel şekillerden oluşur. Alt yapılar dikdörtgenler içinde "yuvalanabilir", ancak bunun için üst yapıdan tek bir çıkış olması gerekir. Semboller ve kanonik yapıları oluşturmak için kullanımları diyagramda gösterilmiştir. ⓘ
Örnekler
Algoritma örneği
En basit algoritmalardan biri, rastgele sıralanmış sayılardan oluşan bir listedeki en büyük sayıyı bulmaktır. Çözümü bulmak için listedeki her sayıya bakmak gerekir. Buradan, İngilizce düzyazıda üst düzey bir tanımla ifade edilebilecek basit bir algoritma ortaya çıkar: Üst düzey açıklama:
- Kümede hiç sayı yoksa en yüksek sayı da yoktur.
- Kümedeki ilk sayının kümedeki en büyük sayı olduğunu varsayalım.
- Kümede kalan her sayı için: eğer bu sayı mevcut en büyük sayıdan daha büyükse, bu sayıyı kümedeki en büyük sayı olarak kabul edin.
- Kümede üzerinde yinelenecek sayı kalmadığında, mevcut en büyük sayıyı kümenin en büyük sayısı olarak kabul edin. ⓘ
(Yarı) resmi açıklama: Düzyazı olarak yazılmış ancak bir bilgisayar programının üst düzey diline çok daha yakın olan aşağıdaki, algoritmanın sözde kod veya pidgin kodunda daha resmi bir kodlamasıdır:
Algoritma En BüyükSayı Girdi: L sayılarından oluşan bir liste. Çıktı: L listesindeki en büyük sayı.
if L.size = 0 return null en büyük ← L[0] L'deki her öğe için şunları yapın öğe > en büyük ise, o zaman en büyük ← öğe return en büyük
- "←" atamayı belirtir. Örneğin, "en büyük ← öğe", en büyük değerinin öğe değerine dönüştüğü anlamına gelir.
- "return" algoritmayı sonlandırır ve aşağıdaki değeri çıktı olarak verir. ⓘ
Öklid'in algoritması
Matematikte Öklid algoritması veya Öklid'in algoritması, iki tam sayının (sayının) en büyük ortak bölenini (GCD) hesaplamak için etkili bir yöntemdir, her ikisini de kalan olmadan bölen en büyük sayıdır. Adını ilk kez Elements (MÖ 300) adlı eserinde tanımlayan antik Yunan matematikçi Öklid'den almıştır. Yaygın kullanımdaki en eski algoritmalardan biridir. Kesirleri en basit biçimlerine indirgemek için kullanılabilir ve diğer birçok sayı teorisi ve kriptografik hesaplamanın bir parçasıdır. ⓘ

Öklid problemi şu şekilde ortaya koyar: "Birbirine asal olmayan iki sayı verildiğinde, bunların en büyük ortak ölçüsünü bulmak". "Bir sayıyı birimlerden oluşan bir çokluk" olarak tanımlar: bir sayma sayısı, sıfır içermeyen pozitif bir tamsayı. "Ölçmek", kalan kısım r kısa uzunluk s'den daha az olana kadar uzun uzunluk l boyunca art arda (q kez) daha kısa bir ölçüm uzunluğu s yerleştirmektir. Modern bir deyişle, kalan r = l - q×s, q bölümdür veya kalan r "modüldür", bölmeden sonra kalan tamsayı-kesirli kısımdır. ⓘ
Öklid'in yönteminin başarılı olabilmesi için başlangıç uzunluklarının iki gereksinimi karşılaması gerekir: (i) uzunluklar sıfır olmamalıdır VE (ii) çıkarma işlemi "doğru" olmalıdır; yani, bir test iki sayıdan küçük olanın büyük olandan çıkarıldığını garanti etmelidir (veya ikisi eşit olabilir, böylece çıkarma işlemi sıfır verir). ⓘ
Öklid'in orijinal ispatına üçüncü bir gereklilik daha eklenmiştir: iki uzunluk birbirine asal olmamalıdır. Öklid bunu, iki sayının ortak ölçüsünün aslında en büyük olduğuna dair bir reductio ad absurdum kanıtı oluşturabilmek için şart koşmuştur. Nicomachus'un algoritması Öklid'inkiyle aynı olsa da, sayılar birbirine asal olduğunda, ortak ölçüleri için "1" sayısını verir. Yani, kesin olmak gerekirse, aşağıdaki gerçekten Nicomachus'un algoritmasıdır. ⓘ

1599 = 650×2 + 299
650 = 299×2 + 52
299 = 52×5 + 39
52 = 39×1 + 13
39 = 13×3 + 0 <span title="Kaynak: İngilizce Vikipedi, Bölüm "Euclid's algorithm"" class="plainlinks">[https://en.wikipedia.org/wiki/Algorithm#Euclid's_algorithm <span style="color:#dddddd">ⓘ</span>]</span>Öklid'in algoritması için bilgisayar dili
Öklid'in algoritmasını çalıştırmak için yalnızca birkaç komut türü gereklidir - bazı mantıksal testler (koşullu GOTO), koşulsuz GOTO, atama (değiştirme) ve çıkarma.
- Bir konum büyük harf(ler) ile sembolize edilir, örneğin S, A, vb.
- Bir konumdaki değişen miktar (sayı) küçük harf(ler) ile yazılır ve (genellikle) konumun adı ile ilişkilendirilir. Örneğin, başlangıçtaki L konumu l = 3009 sayısını içerebilir. ⓘ
Öklid'in algoritması için basit olmayan bir program

Aşağıdaki algoritma Knuth'un Euclid ve Nicomachus'un dört adımlı versiyonu olarak çerçevelenmiştir, ancak kalanı bulmak için bölme kullanmak yerine, r s'den küçük olana kadar kalan r uzunluğundan daha kısa olan s uzunluğunun ardışık çıkarmalarını kullanır. Kalın harflerle gösterilen üst düzey açıklama Knuth 1973: 2-4'ten uyarlanmıştır: GİRİŞ:
1 [İki konuma L ve S iki uzunluğu temsil eden l ve s sayılarını koyun]: GİRİŞ L, S 2 [R'yi başlatın: kalan r uzunluğunu başlangıç/ilk/giriş uzunluğu l'ye eşit yapın]: R ← L ⓘ
E0: [r ≥ s olduğundan emin olun]
3 [İki sayıdan küçük olanın S'de ve büyük olanın R'de olduğundan emin olun]: EĞER R > S SONRA L'nin içeriği daha büyük sayıdır, bu nedenle 4, 5 ve 6. adımları atlayın: GOTO adım 7 ELSE R ve S'nin içeriklerini değiştirin. 4 L ← R (bu ilk adım gereksizdir, ancak daha sonraki tartışma için yararlıdır). 5 R ← S 6 S ← L ⓘ
E1: [Kalanı bul]: R'de kalan r uzunluğu S'deki daha kısa s uzunluğundan daha az olana kadar, S'deki s ölçüm sayısını R'de kalan r uzunluğundan tekrar tekrar çıkarın.
7 EĞER S > R ISE O ZAMAN ölçüm bitti GOTO 10 ELSE tekrar ölç, 8 R ← R - S 9 [Kalan-döngü]: GOTO 7. ⓘ
E2: [Kalan sıfır mı?]: YA (i) son ölçüm tamdı, R'de kalan sıfırdır ve program durdurulabilir, YA DA (ii) algoritma devam etmelidir: son ölçüm R'de S'deki ölçüm sayısından daha az bir kalan bırakmıştır.
10 R = 0 ISE O ZAMAN öyle yaptım GOTO adım 15 ELSE Adım 11'e DEVAM EDİN, ⓘ
E3: [s ve r'yi değiştirin]: Öklid'in algoritmasının somunu. Daha önce daha küçük olan s sayısını ölçmek için kalan r'yi kullanın; L geçici bir konum olarak hizmet eder.
11 L ← R 12 R ← S 13 S ← L 14 [Ölçüm işlemini tekrarlayın]: GOTO 7 ⓘ
ÇIKTI:
15 [Bitti. S en büyük ortak bölen içerir]: PRINT S ⓘ
BİTTİ:
16 DUR, SON, DUR. ⓘ
Öklid'in algoritması için zarif bir program
Öklid'in algoritmasının aşağıdaki versiyonu, "Zarif Olmayan" tarafından yapılması gereken on üç işlemi yapmak için yalnızca altı çekirdek talimat gerektirir; daha da kötüsü, "Zarif Olmayan" daha fazla talimat türü gerektirir. "Zarif "in akış şeması bu makalenin üst kısmında bulunabilir. (Yapılandırılmamış) Basic dilinde, adımlar numaralandırılır ve talimat LET [] = [] ← ile sembolize edilen atama komutudur.
5 REM Öklid'in en büyük ortak bölen algoritması
6 PRINT "0'dan büyük iki tam sayı yazın"
10 GİRİŞ A,B
20 IF B=0 THEN GOTO 80
30 IF A > B THEN GOTO 60
40 LET B=B-A
50 GOTO 20
60 LET A=A-B
70 GOTO 20
80 BASKI A
90 SON"Elegant" nasıl çalışır? Bir dış "Euclid döngüsü" yerine, "Elegant" iki "eş döngü" arasında gidip gelir: A ← A - B'yi hesaplayan bir A > B döngüsü ve B ← B - A'yı hesaplayan bir B ≤ A döngüsü. Bu, en sonunda minuend M, subtrahend S'den küçük veya ona eşit olduğunda (Fark = Minuend - Subtrahend), minuend s (yeni ölçüm uzunluğu) ve subtrahend yeni r (ölçülecek uzunluk) haline gelebildiği için çalışır; başka bir deyişle, çıkarmanın "anlamı" tersine döner. ⓘ
Aşağıdaki versiyon C ailesinden programlama dilleri ile kullanılabilir:
// Öklid'in en büyük ortak bölen algoritması
int euclidAlgorithm (int A, int B){
A=abs(A);
B=abs(B);
while (B!=0){
while (A>B) A=A-B;
B=B-A;
}
A'yı döndür;
} <span title="Kaynak: İngilizce Vikipedi, Bölüm "An elegant program for Euclid's algorithm"" class="plainlinks">[https://en.wikipedia.org/wiki/Algorithm#An_elegant_program_for_Euclid's_algorithm <span style="color:#dddddd">ⓘ</span>]</span>Euclid algoritmalarının test edilmesi
Bir algoritma, yazarının yapmasını istediği şeyi yapıyor mu? Birkaç test vakası genellikle temel işlevsellik konusunda biraz güven verir. Ancak testler yeterli değildir. Test durumları için bir kaynak 3009 ve 884'ü kullanmaktadır. Knuth 40902, 24140'ı önermiştir. Bir başka ilginç durum ise 14157 ve 5950 gibi iki nispeten asal sayıdır. ⓘ
Ancak "istisnai durumlar" tanımlanmalı ve test edilmelidir. "Inelegant" R > S, S > R, R = S olduğunda düzgün çalışacak mı? "Zarif" için de aynı şey geçerli: B > A, A > B, A = B? (Hepsine evet). Bir sayı sıfır olduğunda, her iki sayı da sıfır olduğunda ne olur? ("Inelegant" tüm durumlarda sonsuza kadar hesaplar; "Elegant" A = 0 olduğunda sonsuza kadar hesaplar). Negatif sayılar girilirse ne olur? Kesirli sayılar? Eğer girdi sayıları, yani algoritma/program tarafından hesaplanan fonksiyonun etki alanı, sıfır dahil olmak üzere sadece pozitif tam sayıları içerecekse, o zaman sıfırdaki başarısızlıklar algoritmanın (ve onu örnekleyen programın) toplam bir fonksiyondan ziyade kısmi bir fonksiyon olduğunu gösterir. İstisnalar nedeniyle meydana gelen kayda değer bir başarısızlık Ariane 5 Flight 501 roket arızasıdır (4 Haziran 1996). ⓘ
Matematiksel tümevarım kullanarak program doğruluğunun kanıtlanması: Knuth, matematiksel tümevarımın Öklid algoritmasının "genişletilmiş" bir versiyonuna uygulanmasını göstermiş ve "herhangi bir algoritmanın geçerliliğini kanıtlamak için uygulanabilir genel bir yöntem" önermiştir. Tausworthe, bir programın karmaşıklığının ölçüsünün doğruluk kanıtının uzunluğu olmasını önerir. ⓘ
Euclid algoritmalarının ölçülmesi ve geliştirilmesi
Zarafet (kompaktlık) iyiliğe (hız) karşı: Sadece altı çekirdek talimatıyla "Elegant", on üç talimatla "Inelegant" ile karşılaştırıldığında açık ara galiptir. Ancak, "Zarif olmayan" daha hızlıdır (HALT'a daha az adımda ulaşır). Algoritma analizi bunun neden böyle olduğunu göstermektedir: "Elegant" her çıkarma döngüsünde iki koşullu test yaparken, "Inelegant" yalnızca bir test yapar. Algoritma (genellikle) çok sayıda döngü gerektirdiğinden, ortalama olarak sadece kalan hesaplandıktan sonra ihtiyaç duyulan "B = 0?" testini yapmak için çok zaman harcanmaktadır. ⓘ
Algoritmalar geliştirilebilir mi? Programcı bir programın "uygun" ve "etkili" olduğuna karar verdiğinde -yani yazarının amaçladığı işlevi hesapladığında- o zaman soru şu olur: geliştirilebilir mi? ⓘ
"Inelegant "ın kompaktlığı beş adımın ortadan kaldırılmasıyla geliştirilebilir. Ancak Chaitin, bir algoritmanın kompakt hale getirilmesinin genelleştirilmiş bir algoritma ile otomatikleştirilemeyeceğini kanıtladı; daha ziyade, yalnızca sezgisel olarak yapılabilir; yani, kapsamlı arama (Busy beaver'da bulunabilecek örnekler), deneme yanılma, zeka, içgörü, tümevarımsal akıl yürütme uygulaması vb. ile. 4, 5 ve 6. adımların 11, 12 ve 13. adımlarda tekrarlandığına dikkat edin. "Elegant" ile karşılaştırma, bu adımların 2. ve 3. adımlarla birlikte ortadan kaldırılabileceğine dair bir ipucu sağlar. Bu, çekirdek talimatlarının sayısını on üçten sekize düşürür, bu da onu dokuz adımda "Elegant "tan "daha zarif" yapar. ⓘ
"Elegant "ın hızı, "B=0?" testini iki çıkarma döngüsünün dışına taşıyarak artırılabilir. Bu değişiklik üç talimatın eklenmesini gerektirir (B = 0?, A = 0?, GOTO). Artık "Elegant" örnek sayıları daha hızlı hesaplamaktadır; bunun herhangi bir A, B ve R, S için her zaman geçerli olup olmadığı ayrıntılı bir analiz gerektirecektir. ⓘ
Algoritmik analiz
Belirli bir algoritma için teorik olarak belirli bir kaynağın (zaman veya depolama gibi) ne kadarının gerekli olduğunu bilmek sıklıkla önemlidir. Bu tür nicel cevapları (tahminleri) elde etmek için algoritmaların analizine yönelik yöntemler geliştirilmiştir; örneğin, n sayıdan oluşan bir listenin öğelerini toplayan bir algoritma, büyük O gösterimini kullanarak O(n) zaman gereksinimine sahip olacaktır. Algoritmanın her zaman yalnızca iki değeri hatırlaması gerekir: o ana kadarki tüm elemanların toplamı ve girdi listesindeki mevcut konumu. Bu nedenle, girdi sayılarını saklamak için gereken alan sayılmazsa O(1), sayılırsa O(n) alan gereksinimine sahip olduğu söylenir. ⓘ
Farklı algoritmalar aynı görevi farklı bir dizi talimatla diğerlerinden daha az veya daha fazla zaman, alan veya 'çaba' ile tamamlayabilir. Örneğin, ikili arama algoritması (O(log n) maliyetli), sıralanmış listeler veya diziler üzerinde tablo aramaları için kullanıldığında sıralı aramadan (O(n) maliyetli) daha iyi performans gösterir. ⓘ
Resmi ve ampirik
Algoritmaların analizi ve incelenmesi, bilgisayar bilimlerinin bir disiplinidir ve genellikle belirli bir programlama dili veya uygulaması kullanılmadan soyut olarak uygulanır. Bu anlamda algoritma analizi, belirli bir uygulamanın özelliklerine değil, algoritmanın altında yatan özelliklere odaklanması bakımından diğer matematik disiplinlerine benzemektedir. Genellikle analiz için en basit ve en genel gösterim olduğu için sözde kod kullanılır. Ancak, sonuçta, çoğu algoritma genellikle belirli donanım/yazılım platformlarında uygulanır ve algoritmik verimlilikleri sonunda gerçek kod kullanılarak test edilir. "Tek seferlik" bir problemin çözümü için, belirli bir algoritmanın verimliliğinin önemli sonuçları olmayabilir (n aşırı büyük olmadığı sürece), ancak hızlı etkileşimli, ticari veya uzun ömürlü bilimsel kullanım için tasarlanmış algoritmalar için kritik olabilir. Küçük n'den büyük n'ye ölçeklendirme, aksi takdirde zararsız olan verimsiz algoritmaları sıklıkla ortaya çıkarır. ⓘ
Ampirik testler faydalıdır çünkü performansı etkileyen beklenmedik etkileşimleri ortaya çıkarabilir. Benchmarklar, program optimizasyonundan sonra bir algoritmadaki potansiyel iyileştirmelerin öncesi/sonrasını karşılaştırmak için kullanılabilir. Ancak ampirik testler resmi analizin yerini alamaz ve adil bir şekilde gerçekleştirilmesi önemsiz değildir. ⓘ
Yürütme verimliliği
Köklü algoritmalarda bile mümkün olan potansiyel iyileştirmeleri göstermek için, FFT algoritmalarıyla ilgili (görüntü işleme alanında yoğun olarak kullanılan) son önemli bir yenilik, tıbbi görüntüleme gibi uygulamalar için işlem süresini 1.000 kata kadar azaltabilir. Genel olarak, hız iyileştirmeleri, pratik uygulamalarda çok yaygın olan problemin özel özelliklerine bağlıdır. Bu büyüklükteki hız artışları, görüntü işlemeyi yoğun olarak kullanan bilgisayar cihazlarının (dijital kameralar ve tıbbi ekipmanlar gibi) daha az güç tüketmesini sağlar. ⓘ
Sınıflandırma
Algoritmaları sınıflandırmanın çeşitli yolları vardır ve her birinin kendine has özellikleri vardır. ⓘ
Uygulamaya göre
Algoritmaları sınıflandırmanın bir yolu da uygulama araçlarına göre sınıflandırmaktır. ⓘ
int gcd(int A, int B) {
eğer (B == 0)
A'yı döndür;
else if (A > B)
return gcd(A-B,B);
else
return gcd(A,B-A);
} <span title="Kaynak: İngilizce Vikipedi, Bölüm "By implementation"" class="plainlinks">[https://en.wikipedia.org/wiki/Algorithm#By_implementation <span style="color:#dddddd">ⓘ</span>]</span> |
| Yukarıdaki akış şemasından Öklid algoritmasının özyinelemeli C uygulaması |
- Özyineleme
- Özyinelemeli bir algoritma, belirli bir koşul (sonlandırma koşulu olarak da bilinir) eşleşene kadar kendisini tekrar tekrar çağıran (referans yapan) bir algoritmadır ve fonksiyonel programlamada yaygın olarak kullanılan bir yöntemdir. Yinelemeli algoritmalar, verilen problemleri çözmek için döngüler gibi tekrarlayan yapılar ve bazen yığınlar gibi ek veri yapıları kullanır. Bazı problemler doğal olarak bir uygulama ya da diğeri için uygundur. Örneğin, Hanoi Kuleleri özyinelemeli uygulama kullanılarak iyi anlaşılmıştır. Her özyinelemeli versiyonun eşdeğer (ancak muhtemelen daha fazla veya daha az karmaşık) bir yinelemeli versiyonu vardır ve bunun tersi de geçerlidir.
- Mantıksal
- Bir algoritma, kontrollü mantıksal çıkarım olarak görülebilir. Bu kavram şu şekilde ifade edilebilir: Algoritma = mantık + kontrol. Mantık bileşeni hesaplamada kullanılabilecek aksiyomları ifade eder ve kontrol bileşeni aksiyomlara tümdengelimin uygulanma şeklini belirler. Bu, mantık programlama paradigmasının temelini oluşturur. Saf mantık programlama dillerinde, kontrol bileşeni sabittir ve algoritmalar yalnızca mantık bileşeni sağlanarak belirtilir. Bu yaklaşımın cazibesi zarif semantiğidir: aksiyomlardaki bir değişiklik algoritmada iyi tanımlanmış bir değişiklik üretir.
- Seri, paralel veya dağıtılmış
- Algoritmalar genellikle bilgisayarların bir seferde bir algoritma komutu yürüttüğü varsayımıyla tartışılır. Bu bilgisayarlar bazen seri bilgisayarlar olarak adlandırılır. Böyle bir ortam için tasarlanmış bir algoritma, paralel algoritmaların veya dağıtılmış algoritmaların aksine seri algoritma olarak adlandırılır. Paralel algoritmalar, birkaç işlemcinin aynı anda bir problem üzerinde çalışabildiği bilgisayar mimarilerinden yararlanırken, dağıtılmış algoritmalar bir bilgisayar ağına bağlı birden fazla makineyi kullanır. Paralel veya dağıtık algoritmalar problemi daha simetrik veya asimetrik alt problemlere böler ve sonuçları tekrar bir araya toplar. Bu tür algoritmalarda kaynak tüketimi sadece her bir işlemcideki işlemci döngüleri değil, aynı zamanda işlemciler arasındaki iletişim ek yüküdür. Bazı sıralama algoritmaları verimli bir şekilde paralelleştirilebilir, ancak iletişim ek yükleri pahalıdır. Yinelemeli algoritmalar genellikle paralelleştirilebilir. Bazı problemler paralel algoritmalara sahip değildir ve doğası gereği seri problemler olarak adlandırılır.
- Deterministik veya deterministik olmayan
- Deterministik algoritmalar problemi algoritmanın her adımında kesin karar vererek çözerken, deterministik olmayan algoritmalar problemleri tahmin yoluyla çözer, ancak tipik tahminler sezgisel yöntemler kullanılarak daha doğru hale getirilir.
- Kesin veya yaklaşık
- Birçok algoritma kesin bir çözüme ulaşırken, yaklaşım algoritmaları gerçek çözüme daha yakın bir yaklaşım arar. Bu yaklaşıma deterministik ya da rastgele bir strateji kullanılarak ulaşılabilir. Bu tür algoritmalar birçok zor problem için pratik değere sahiptir. Yaklaşık algoritma örneklerinden biri, verilen öğelerden oluşan bir kümenin bulunduğu Knapsack problemidir. Amacı, maksimum toplam değeri elde etmek için sırt çantasını paketlemektir. Her öğenin bir ağırlığı ve bir değeri vardır. Taşınabilecek toplam ağırlık sabit bir X sayısından fazla olamaz. Bu nedenle çözüm, öğelerin ağırlıklarının yanı sıra değerlerini de dikkate almalıdır.
- Kuantum algoritması
- Gerçekçi bir kuantum hesaplama modeli üzerinde çalışırlar. Bu terim genellikle doğası gereği kuantum gibi görünen veya kuantum süperpozisyon veya kuantum dolaşıklık gibi Kuantum hesaplamanın bazı temel özelliklerini kullanan algoritmalar için kullanılır. ⓘ
Tasarım paradigmasına göre
Algoritmaları sınıflandırmanın bir başka yolu da tasarım metodolojileri veya paradigmalarıdır. Her biri diğerinden farklı olan belirli sayıda paradigma vardır. Ayrıca, bu kategorilerin her biri birçok farklı algoritma türünü içerir. Bazı yaygın paradigmalar şunlardır:
- Kaba kuvvet veya kapsamlı arama
- Bu, hangisinin en iyi olduğunu görmek için mümkün olan her çözümü denemeye yönelik naif bir yöntemdir.
- Böl ve fethet
- Bir böl ve yönet algoritması, bir problemin bir örneğini, örnekler kolayca çözülebilecek kadar küçük olana kadar aynı problemin bir veya daha fazla küçük örneğine (genellikle özyinelemeli olarak) tekrar tekrar indirger. Böl ve yönet algoritmasının bir örneği birleştirme sıralamasıdır. Veriler segmentlere ayrıldıktan sonra her bir veri segmenti üzerinde sıralama yapılabilir ve segmentler birleştirilerek fethetme aşamasında tüm verilerin sıralaması elde edilebilir. Böl ve fethet algoritmasının daha basit bir çeşidi, özdeş bir alt problemi çözen ve bu alt problemin çözümünü daha büyük problemi çözmek için kullanan azalt ve fethet algoritması olarak adlandırılır. Böl ve fethet, problemi birden fazla alt probleme böler ve bu nedenle fethetme aşaması azalt ve fethet algoritmalarından daha karmaşıktır. Azalt ve fethet algoritmasına örnek olarak ikili arama algoritması verilebilir.
- Arama ve numaralandırma
- Birçok problem (satranç oynamak gibi) çizge problemleri olarak modellenebilir. Bir çizge keşif algoritması, bir çizge etrafında hareket etmek için kuralları belirtir ve bu tür problemler için kullanışlıdır. Bu kategori aynı zamanda arama algoritmalarını, dal ve sınır numaralandırmayı ve geri izlemeyi de içerir.
- Rastgele algoritma
- Bu tür algoritmalar bazı seçimleri rasgele (veya sözde rasgele) yapar. Kesin çözümler bulmanın pratik olmadığı problemler için yaklaşık çözümler bulmada çok faydalı olabilirler (aşağıdaki sezgisel yönteme bakınız). Bu problemlerden bazıları için en hızlı yaklaşımların bir miktar rastgelelik içermesi gerektiği bilinmektedir. Polinom zaman karmaşıklığına sahip rastgele algoritmaların bazı problemler için en hızlı algoritmalar olup olamayacağı, P'ye karşı NP problemi olarak bilinen açık bir sorudur. Bu tür algoritmaların iki büyük sınıfı vardır:
- Monte Carlo algoritmaları yüksek olasılıkla doğru bir cevap döndürür. Örneğin RP, bunların polinom zamanda çalışan alt sınıfıdır.
- Las Vegas algoritmaları her zaman doğru yanıtı verir, ancak çalışma süreleri yalnızca olasılıksal olarak sınırlıdır, örneğin ZPP.
- Karmaşıklığın azaltılması
- Bu teknik, zor bir problemi (umarım) asimptotik olarak optimal algoritmalara sahip olduğumuz daha iyi bilinen bir probleme dönüştürerek çözmeyi içerir. Amaç, karmaşıklığı elde edilen indirgenmiş algoritmanın karmaşıklığı tarafından domine edilmeyen bir indirgeme algoritması bulmaktır. Örneğin, sıralanmamış bir listede medyanı bulmak için kullanılan bir seçim algoritması, önce listeyi sıralamayı (pahalı kısım) ve ardından sıralanmış listedeki orta elemanı (ucuz kısım) çıkarmayı içerir. Bu teknik dönüştür ve fethet olarak da bilinir.
- Geri izleme
- Bu yaklaşımda, çoklu çözümler aşamalı olarak oluşturulur ve geçerli bir tam çözüme yol açamayacakları belirlendiğinde terk edilir. ⓘ
Optimizasyon problemleri
Optimizasyon problemleri için algoritmaların daha spesifik bir sınıflandırması vardır; bu tür problemler için bir algoritma yukarıda açıklanan genel kategorilerden bir veya daha fazlasına girebileceği gibi aşağıdakilerden birine de girebilir:
- Doğrusal programlama
- Doğrusal eşitlik ve eşitsizlik kısıtlarına bağlı doğrusal bir fonksiyona optimal çözümler ararken, problemin kısıtları optimal çözümlerin üretilmesinde doğrudan kullanılabilir. Popüler simpleks algoritması gibi bu kategorideki herhangi bir problemi çözebilen algoritmalar vardır. Doğrusal programlama ile çözülebilen problemler arasında yönlendirilmiş grafikler için maksimum akış problemi yer alır. Eğer bir problem ek olarak bilinmeyenlerden bir veya daha fazlasının tamsayı olmasını gerektiriyorsa, o zaman tamsayı programlama olarak sınıflandırılır. Bir doğrusal programlama algoritması, tamsayı değerleri için tüm kısıtlamaların yüzeysel olduğu, yani çözümlerin bu kısıtlamaları her halükarda karşıladığı kanıtlanabilirse böyle bir problemi çözebilir. Genel durumda, problemin zorluğuna bağlı olarak özel bir algoritma veya yaklaşık çözümler bulan bir algoritma kullanılır.
- Dinamik programlama
- Bir problem optimal alt yapılar gösterdiğinde -yani bir problemin optimal çözümü alt problemlerin optimal çözümlerinden oluşturulabildiğinde- ve alt problemler üst üste geldiğinde, yani aynı alt problemler birçok farklı problem örneğini çözmek için kullanıldığında, dinamik programlama adı verilen daha hızlı bir yaklaşım, daha önce hesaplanmış olan çözümlerin yeniden hesaplanmasını önler. Örneğin, Floyd-Warshall algoritması, ağırlıklı bir grafikteki bir köşeden hedefe giden en kısa yol, tüm komşu köşelerden hedefe giden en kısa yol kullanılarak bulunabilir. Dinamik programlama ve memoization birlikte çalışır. Dinamik programlama ile böl ve yönet arasındaki temel fark, böl ve yönet yönteminde alt problemlerin az çok bağımsız olması, dinamik programlamada ise alt problemlerin üst üste gelmesidir. Dinamik programlama ile basit özyineleme arasındaki fark, özyinelemeli çağrıların önbelleğe alınması veya hafızaya alınmasıdır. Alt problemler bağımsız olduğunda ve tekrarlama olmadığında, memoizasyon yardımcı olmaz; bu nedenle dinamik programlama tüm karmaşık problemler için bir çözüm değildir. Memoizasyon kullanarak ya da daha önce çözülmüş alt problemlerin bir tablosunu tutarak, dinamik programlama birçok problemin üstel doğasını polinom karmaşıklığına indirger.
- Açgözlü yöntem
- Açgözlü algoritma, dinamik programlama algoritmasına benzer, çünkü bu durumda problemin değil, verilen bir çözümün alt yapılarını inceleyerek çalışır. Bu tür algoritmalar, verilmiş veya bir şekilde oluşturulmuş bir çözümle başlar ve küçük değişiklikler yaparak onu geliştirir. Bazı problemler için en uygun çözümü bulabilirken, diğerleri için yerel optimumlarda, yani algoritma tarafından iyileştirilemeyen ancak optimum olmayan çözümlerde dururlar. Açgözlü algoritmaların en popüler kullanımı, bu yöntemle optimum çözümü bulmanın mümkün olduğu minimal yayılan ağacı bulmak içindir. Huffman Tree, Kruskal, Prim, Sollin bu optimizasyon problemini çözebilen açgözlü algoritmalardır.
- Sezgisel yöntem
- Optimizasyon problemlerinde, optimum çözümü bulmanın pratik olmadığı durumlarda optimum çözüme yakın bir çözüm bulmak için sezgisel algoritmalar kullanılabilir. Bu algoritmalar, ilerledikçe optimum çözüme daha da yaklaşarak çalışırlar. Prensip olarak, sonsuz bir süre boyunca çalıştırılırlarsa, optimum çözümü bulacaklardır. Avantajları, nispeten kısa bir sürede optimum çözüme çok yakın bir çözüm bulabilmeleridir. Bu tür algoritmalar arasında yerel arama, tabu arama, benzetimli tavlama ve genetik algoritmalar bulunmaktadır. Tavlama benzetimi gibi bazıları deterministik olmayan algoritmalar iken, tabu arama gibi diğerleri deterministiktir. Optimal olmayan çözümün hatası üzerinde bir sınır bilindiğinde, algoritma ayrıca bir yaklaşım algoritması olarak kategorize edilir. ⓘ
Çalışma alanına göre
Her bilim alanının kendine özgü problemleri vardır ve verimli algoritmalara ihtiyaç duyar. Bir alandaki ilgili problemler genellikle birlikte çalışılır. Arama algoritmaları, sıralama algoritmaları, birleştirme algoritmaları, sayısal algoritmalar, çizge algoritmaları, dizgi algoritmaları, hesaplamalı geometrik algoritmalar, kombinatoryal algoritmalar, tıbbi algoritmalar, makine öğrenimi, kriptografi, veri sıkıştırma algoritmaları ve ayrıştırma teknikleri bazı örnek sınıflardır. ⓘ
Alanlar birbirleriyle örtüşme eğilimindedir ve bir alandaki algoritma ilerlemeleri, bazen tamamen ilgisiz olan diğer alanların algoritmalarını geliştirebilir. Örneğin, dinamik programlama endüstride kaynak tüketiminin optimizasyonu için icat edilmiştir ancak şu anda birçok alanda geniş bir yelpazedeki problemlerin çözümünde kullanılmaktadır. ⓘ
Karmaşıklığa göre
Algoritmalar, girdi boyutlarına kıyasla tamamlamak için ihtiyaç duydukları süreye göre sınıflandırılabilir:
- Sabit zaman: Girdi boyutundan bağımsız olarak algoritmanın ihtiyaç duyduğu zaman aynıysa. Örneğin bir dizi elemanına erişim.
- Logaritmik zaman: zaman girdi boyutunun logaritmik bir fonksiyonu ise. Örn. ikili arama algoritması.
- Doğrusal zaman: zaman girdi boyutuyla orantılıysa. Örn. bir listenin çaprazlanması.
- Polinom zaman: zaman girdi boyutunun bir kuvveti ise. Örn. kabarcık sıralama algoritması ikinci dereceden zaman karmaşıklığına sahiptir.
- Üstel zaman: zaman girdi boyutunun üstel bir fonksiyonu ise. Örn. kaba kuvvet arama. ⓘ
Bazı problemlerin farklı karmaşıklıkta birden fazla algoritması olabilirken, diğer problemlerin hiçbir algoritması olmayabilir veya bilinen verimli algoritmaları bulunmayabilir. Ayrıca bazı problemlerden diğer problemlere eşlemeler de vardır. Bu nedenle, algoritmalar yerine problemlerin kendilerini, onlar için mümkün olan en iyi algoritmaların karmaşıklığına dayalı eşdeğerlik sınıflarına sınıflandırmanın daha uygun olduğu görülmüştür. ⓘ
Sürekli algoritmalar
"Algoritma" kelimesine uygulandığında "sürekli" sıfatı şu anlama gelebilir:
- Sürekli nicelikleri temsil eden veriler üzerinde çalışan bir algoritma, bu veriler ayrık yaklaşımlarla temsil edilse bile - bu tür algoritmalar sayısal analizde incelenir; veya
- Analog bir bilgisayarda çalışan, veriler üzerinde sürekli olarak çalışan diferansiyel denklem biçiminde bir algoritma. ⓘ
Hukuki Konular
Algoritmalar, tek başlarına, genellikle patent verilebilir değildirler. Amerika Birleşik Devletleri'nde soyut kavramların, sayıların ve işaretlerin yalnızca basit yönlendirmelerinden oluşan bir iddia "süreç" oluşturmaz (USPTO 2006) ve bundan dolayı algoritmalar patent verilebilir değildir (Gottschalk v.Benson'da olduğu gibi). Bununla birlikte, algoritmanın pratik uygulamaları zaman zaman patent verilebilirdir. Örneğin, Diamond v.Diehr'da, sentetik kauçuğun muhafaza edilmesine yardımcı olmak için kullanılan basit geri bildirim algoritmasının uygulaması patent verilebilir sayılmıştır. Yazılım patenti son derece tartışmalıdır ve algoritmaları içeren birçok eleştirilmiş patent vardır, özellikle veri sıkıştırma algoritmaları, Unisys' LZW patentinde olduğu gibi. ⓘ
Ek olarak, bazı kriptografik algoritmaların ihracat kısıtlamaları vardır. ⓘ
Tarihçe: "Algoritma" kavramının gelişimi
Antik Yakın Doğu
Algoritmaların en eski kanıtları eski Mezopotamya'nın (modern Irak) Babil matematiğinde bulunur. Bağdat yakınlarındaki Şuruppak'ta bulunan ve MÖ 2500'lere tarihlenen bir Sümer kil tableti en eski bölme algoritmasını tanımlamaktadır. Hammurabi hanedanlığı döneminde, yaklaşık MÖ 1800-1600 yılları arasında, Babil kil tabletlerinde formüllerin hesaplanmasına yönelik algoritmalar tanımlanmıştır. Algoritmalar Babil astronomisinde de kullanılmıştır. Babil kil tabletleri, önemli astronomik olayların zamanını ve yerini hesaplamak için algoritmik prosedürleri tanımlamakta ve kullanmaktadır. ⓘ
Aritmetik algoritmaları, M.Ö. 1550'lerde Rhind Matematik Papirüsü'ne kadar uzanan eski Mısır matematiğinde de bulunur. Algoritmalar daha sonra antik Helenistik matematikte de kullanılmıştır. Nicomachus'un Aritmetiğe Giriş'inde tanımlanan Eratosthenes'in eleği ve ilk kez Öklid'in Elementler'inde (yaklaşık MÖ 300) tanımlanan Öklid algoritması buna iki örnektir. ⓘ
Ayrık ve ayırt edilebilir semboller
Çetele işaretleri: Eskiler sürülerini, tahıl çuvallarını ve paralarını takip etmek için çetele tutmayı kullanmışlardır: taşları biriktirmek ya da çubuklara işaretler kazımak veya kilden ayrı semboller yapmak. Babil ve Mısırlıların işaret ve sembolleri kullanmasıyla, sonunda Roma rakamları ve abaküs gelişmiştir (Dilson, s. 16-41). Çetele işaretleri, Turing makinesi ve Post-Turing makinesi hesaplamalarında kullanılan tek sayı sistemi aritmetiğinde belirgin bir şekilde görülür. ⓘ
Sayılar için "yer tutucular" olarak sembollerin manipülasyonu: cebir
İranlı bir matematikçi olan Muhammed ibn Mūsā al-Khwārizmī, 9. yüzyılda Al-jabr'ı yazmıştır. "Algoritma" ve "algoritma" terimleri el-Hârizmî isminden, "cebir" terimi ise el-Cebr kitabından türetilmiştir. Avrupa'da "algoritma" kelimesi başlangıçta Harezmî'nin cebirsel denklemleri çözmek için kullandığı kurallar ve teknikler kümesini ifade etmek için kullanılmış, daha sonra herhangi bir kurallar veya teknikler kümesini ifade edecek şekilde genelleştirilmiştir. Bu nihayetinde Leibniz'in calculus ratiocinator (yaklaşık 1680) kavramıyla sonuçlandı:
Zamanının bir buçuk asır ilerisinde olan Leibniz, sıradan cebirin sayıları manipüle etme kurallarını belirlediği gibi mantıksal kavramları manipüle etme kurallarını belirleyecek bir mantık cebiri önermiştir. ⓘ
Kriptografik algoritmalar
Şifreli kodların çözülmesine yönelik ilk kriptografik algoritma, 9. yüzyılda yaşamış bir Arap matematikçi olan Al-Kindi tarafından Kriptografik Mesajların Deşifresi Üzerine Bir El Yazması adlı eserinde geliştirilmiştir. Kindi, en eski şifre çözme algoritması olan frekans analizi ile kriptanalizin ilk tanımını yapmıştır. ⓘ
Ayrık durumlara sahip mekanik düzenekler
Saat: Bolter, ağırlık tahrikli saatin icadını, özellikle de bize mekanik bir saatin tik taklarını sağlayan eşapmanlı saatin icadını "[Orta Çağ'da Avrupa'nın] en önemli icadı" olarak nitelendirmektedir. "Doğru otomatik makine", 13. yüzyıldan itibaren hemen "mekanik otomatlara" ve nihayet 19. yüzyılın ortalarında Charles Babbage ve Kontes Ada Lovelace'ın fark motoru ve analitik motorları olan "hesaplama makinelerine" yol açmıştır. Lovelace, bir bilgisayarda işlenmek üzere tasarlanmış bir algoritmanın ilk yaratıcısı olarak kabul edilir - Babbage'ın analitik motoru, sadece bir hesap makinesi yerine gerçek bir Turing-tam bilgisayarı olarak kabul edilen ilk cihazdır ve bu nedenle bazen "tarihin ilk programcısı" olarak adlandırılır, ancak Babbage'ın ikinci cihazının tam bir uygulaması onun yaşamından onlarca yıl sonrasına kadar gerçekleştirilemeyecektir. ⓘ
Mantıksal makineler 1870 - Stanley Jevons'ın "mantıksal abaküsü" ve "mantıksal makinesi": Teknik sorun, Boole denklemlerinin günümüzde Karnaugh haritaları olarak bilinen biçime benzer bir biçimde sunulduğunda indirgenmesiydi. Jevons (1880) ilk olarak, "[mantıksal] kombinasyonların herhangi bir bölümünün veya sınıfının mekanik olarak seçilebilmesi için tasarlanmış, iğnelerle donatılmış tahta parçalarından" oluşan basit bir "abaküs" tarif eder. Ancak daha yakın zamanda, sistemi tamamen mekanik bir forma indirgedim ve böylece dolaylı çıkarım sürecinin tamamını Mantıksal Makine olarak adlandırılabilecek bir şeyde somutlaştırdım." Makinesi "bazı hareketli ahşap çubuklarla" donatılmıştı ve "ayağında bir piyanodaki gibi 21 tuş vardı [vb.] ...". Bu makine ile "bir kıyası ya da başka herhangi bir basit mantıksal argümanı" analiz edebiliyordu. ⓘ
Bu makineyi 1870 yılında Royal Society üyeleri önünde sergiledi. Ancak bir başka mantıkçı John Venn, 1881 tarihli Symbolic Logic (Sembolik Mantık) adlı eserinde bu çabaya sarılıkla bakmıştır: "Bazen mantıksal makineler olarak adlandırılan şeylerin ilgisi ya da önemi konusunda benim de yüksek bir tahminim yok ... bana öyle geliyor ki şu anda bilinen ya da keşfedilmesi muhtemel herhangi bir düzenek mantıksal makineler adını gerçekten hak etmiyor"; daha fazlası için Algoritma karakterizasyonlarına bakın. Ama o da geri kalmamak için "Profesör Jevon'un abaküsüne biraz benzeyen bir plan sundu ... [Profesör Jevons'ın mantıksal makinesine karşılık gelen aşağıdaki düzenek tanımlanabilir. Ben buna sadece bir mantıksal diyagram makinesi demeyi tercih ediyorum ... ama sanırım herhangi bir mantıksal makineden rasyonel olarak beklenebilecek her şeyi eksiksiz olarak yapabilir". ⓘ
Jakarlı dokuma tezgahı, Hollerith delikli kartları, telgraf ve telefon - elektromekanik röle: Bell ve Newell (1971), Hollerith kartlarının (delikli kartlar, 1887) öncüsü olan Jacquard dokuma tezgahının (1801) ve "telefon anahtarlama teknolojilerinin" ilk bilgisayarların geliştirilmesine yol açan bir ağacın kökleri olduğunu belirtmektedir. 19. yüzyılın ortalarına gelindiğinde, telefonun öncüsü olan telgraf tüm dünyada kullanılıyordu ve harflerin "noktalar ve çizgiler" olarak ayrık ve ayırt edilebilir şekilde kodlanması yaygın bir sesti. 19. yüzyılın sonlarına gelindiğinde, 1890 ABD nüfus sayımında Hollerith kartlarının kullanılması gibi, şerit bant (yaklaşık 1870'ler) kullanılıyordu. Ardından teleprinter (yaklaşık 1910), Baudot kodunun bant üzerinde delikli kağıt kullanımı ile geldi. ⓘ
Dijital toplama cihazının mucidi George Stibitz'in (1937) çalışmalarının arkasında elektromekanik rölelerden oluşan telefon anahtarlama ağları (icat tarihi 1835) vardı. Bell Laboratuarlarında çalışırken, dişlileri olan mekanik hesap makinelerinin "külfetli" kullanımını gözlemledi. "1937'de bir akşam, fikrini test etmek niyetiyle evine gitti... Tamirat bittiğinde, Stibitz ikili bir toplama cihazı inşa etmişti". ⓘ
Matematikçi Martin Davis, elektromekanik rölenin (açık ve kapalı iki "ikili durumu" ile) özel önemini gözlemler:
- Babbage'ın öngördüğü kapsamda makineler ancak 1930'lardan itibaren elektrik röleleri kullanan elektromekanik hesap makinelerinin geliştirilmesiyle yapılabilmiştir." ⓘ
19. yüzyıldan 20. yüzyılın ortalarına kadar matematik
Semboller ve kurallar: George Boole (1847, 1854), Gottlob Frege (1879) ve Giuseppe Peano'nun (1888-1889) matematiği, aritmetiği kurallar tarafından manipüle edilen bir dizi sembole indirgedi. Peano'nun The principles of arithmetic, presented by a new method (1888) adlı kitabı "matematiğin sembolik bir dille aksiyomatize edilmesine yönelik ilk girişim" olmuştur. ⓘ
Ancak Heijenoort bu övgüyü Frege'ye (1879) verir: Frege'nin eseri "belki de mantık alanında yazılmış en önemli tek eserdir. ... içinde bir 'formül dili', yani bir lingua characterica, özel sembollerle yazılmış, "saf düşünce için", yani retorik süslemelerden arınmış bir dil görüyoruz ... belirli kurallara göre manipüle edilen belirli sembollerden inşa edilmiştir". Frege'nin çalışmaları Alfred North Whitehead ve Bertrand Russell tarafından Principia Mathematica (1910-1913) adlı eserlerinde daha da basitleştirilmiş ve genişletilmiştir. ⓘ
Paradokslar: Aynı zamanda literatürde, özellikle Burali-Forti paradoksu (1897), Russell paradoksu (1902-03) ve Richard Paradoksu gibi bir dizi rahatsız edici paradoks ortaya çıkmıştır. Sonuçta ortaya çıkan düşünceler Kurt Gödel'in (1931) -özellikle yalancı paradoksuna atıfta bulunur- özyineleme kurallarını tamamen sayılara indirgeyen makalesine yol açtı. ⓘ
Etkin hesaplanabilirlik: Hilbert tarafından 1928'de kesin olarak tanımlanan Entscheidungsproblemini çözme çabası içinde, matematikçiler ilk olarak "etkili yöntem" veya "etkili hesaplama" veya "etkili hesaplanabilirlik" (yani başarılı olacak bir hesaplama) ile neyin kastedildiğini tanımlamaya koyuldular. Hızlı bir şekilde aşağıdakiler ortaya çıktı: Alonzo Church, Stephen Kleene ve J.B. Rosser'in λ-hesabı, Jacques Herbrand'ın önerileri üzerine hareket eden Gödel'in çalışmalarından (Gödel'in 1934 Princeton derslerine bakınız) ve Kleene'in sonraki basitleştirmelerinden "genel özyinelemenin" ince bir şekilde bilenmiş bir tanımıdır. Church'ün Entscheidungsproblem'in çözülemez olduğunu kanıtlaması, Emil Post'un etkin hesaplanabilirliği, bir işçinin bir dizi oda boyunca sola veya sağa hareket etmek için bir talimat listesini akılsızca takip etmesi ve oradayken bir kağıdı işaretlemesi veya silmesi ya da kağıdı gözlemlemesi ve bir sonraki talimat hakkında evet-hayır kararı vermesi olarak tanımlaması. Alan Turing'in Entscheidungsproblem'in "a- [otomatik-] makine "sini kullanarak çözülemez olduğunu kanıtlaması - aslında Post'un "formülasyonu", J. Barkley Rosser'in "bir makine" açısından "etkili yöntem" tanımıyla neredeyse aynıdır. Kleene'in "Tez I" adını verdiği "Church tezi "nin öncülü olan bir tez önermesi ve birkaç yıl sonra Kleene'in kendi tezinin adını "Church Tezi" olarak değiştirerek "Turing Tezi "ni önermesi. ⓘ
Emil Post (1936) ve Alan Turing (1936-37, 1939)
Emil Post (1936) bir "bilgisayarın" (insanın) eylemlerini şu şekilde tanımlamıştır:
- "...iki kavram söz konusudur: problemden cevaba giden çalışmanın yürütüleceği bir sembol uzayı ve sabit, değiştirilemez bir yönler kümesi. ⓘ
Onun sembol uzayı şöyle olacaktır
- "iki yönlü sonsuz bir uzay ya da kutular dizisi... Problem çözücü ya da işçi bu sembol uzayında hareket edecek ve çalışacak, aynı anda yalnızca bir kutuda bulunabilecek ve çalışabilecektir.... bir kutu yalnızca iki olası durumu kabul edecektir, yani boş ya da işaretsiz olmak ve içinde tek bir işaret, örneğin dikey bir vuruş bulundurmak. ⓘ
- "Bir kutu seçilecek ve başlangıç noktası olarak adlandırılacaktır. ...belirli bir problem, sonlu sayıda kutunun [yani GİRİŞ'in] bir vuruşla işaretlenmesiyle sembolik biçimde verilecektir. Aynı şekilde, cevap da [yani ÇIKTI] böyle bir işaretli kutular konfigürasyonu ile sembolik biçimde verilecektir... ⓘ
- "Genel bir probleme uygulanabilen bir dizi yönerge, her bir özel probleme uygulandığında deterministik bir süreç oluşturur. Bu süreç yalnızca (C) tipi yöne [yani DUR] gelindiğinde sonlanır". Daha fazlasını görmek için Post-Turing makinesi ⓘ

Alan Turing'in çalışması Stibitz'inkinden (1937) önceydi; Stibitz'in Turing'in çalışmasından haberdar olup olmadığı bilinmemektedir. Turing'in biyografi yazarı, Turing'in daktilo benzeri bir model kullanmasının gençlik ilgisinden kaynaklandığına inanıyordu: "Alan çocukken daktilo icat etmeyi hayal etmişti; Bayan Turing'in de bir daktilosu vardı ve Turing işe daktiloya 'mekanik' demenin ne anlama geldiğini kendine sorarak başlamış olabilir". O dönemde Mors alfabesinin, telgrafın, şeritli makinelerin ve teletypewriter'ların yaygınlığı göz önüne alındığında, tüm bunların Turing'i gençliğinde etkilemiş olması oldukça olasıdır. ⓘ
Turing -ki onun hesaplama modeli artık Turing makinesi olarak adlandırılmaktadır- Post gibi, basit bir dizi temel hareket ve "zihin durumuna" indirgediği bir insan bilgisayarı analiziyle başlar. Ancak bir adım daha ileri giderek sayıların hesaplanmasının bir modeli olarak bir makine yaratıyor. ⓘ
- "Hesaplama normalde kağıt üzerine belirli semboller yazılarak yapılır. Bu kağıdın bir çocuğun aritmetik kitabı gibi karelere bölündüğünü varsayabiliriz... O halde hesaplamanın tek boyutlu bir kağıt üzerinde, yani karelere bölünmüş bir bant üzerinde yapıldığını varsayıyorum. Ayrıca basılabilecek sembol sayısının da sonlu olduğunu varsayacağım... ⓘ
- "Bilgisayarın herhangi bir andaki davranışı, gözlemlediği semboller ve o andaki "zihin durumu" tarafından belirlenir. Bilgisayarın bir anda gözlemleyebileceği sembol ya da kare sayısının bir B sınırı olduğunu varsayabiliriz. Eğer daha fazlasını gözlemlemek isterse, birbirini izleyen gözlemleri kullanmalıdır. Ayrıca dikkate alınması gereken zihin durumlarının sayısının da sonlu olduğunu varsayacağız... ⓘ
- "Bilgisayar tarafından gerçekleştirilen işlemlerin 'basit işlemlere' bölündüğünü düşünelim; bu işlemler o kadar temeldir ki, daha fazla bölünmelerini hayal etmek kolay değildir." ⓘ
Turing'in indirgemesi aşağıdaki sonucu verir:
- "Bu nedenle basit işlemler şunları içermelidir:
- "(a) Gözlemlenen karelerden birinin üzerindeki sembolün değiştirilmesi
- "(b) Gözlemlenen karelerden birinin, daha önce gözlemlenen karelerden birinin L karesi içindeki başka bir kareye değişmesi.
"Bu değişikliklerden bazıları zorunlu olarak bir zihin durumu değişikliğine yol açıyor olabilir. Bu nedenle en genel tek işlem aşağıdakilerden biri olarak alınmalıdır:
- "(A) Olası bir zihin durumu değişikliği ile birlikte olası bir sembol değişikliği (a).
- "(B) Olası bir zihin durumu değişikliği ile birlikte gözlemlenen karelerin olası bir değişikliği (b)" ⓘ
- "Şimdi bu bilgisayarın yaptığı işi yapacak bir makine inşa edebiliriz." ⓘ
Birkaç yıl sonra Turing, analizini (tezini, tanımını) şu güçlü ifadeyle genişletti:
- "Bir fonksiyonun değerleri tamamen mekanik bir işlemle bulunabiliyorsa, o fonksiyonun "etkin bir şekilde hesaplanabilir" olduğu söylenir. Bu fikri sezgisel olarak kavramak oldukça kolay olsa da, yine de daha kesin, matematiksel olarak ifade edilebilir bir tanıma sahip olmak arzu edilir ... [Gödel, Herbrand, Kleene, Church, Turing ve Post ile ilgili olarak tanımın tarihini hemen hemen yukarıda sunulduğu şekilde tartışmaktadır] ... Bu ifadeyi kelimesi kelimesine ele alarak, tamamen mekanik bir süreçten bir makine tarafından gerçekleştirilebilecek bir süreci anlayabiliriz. Bu makinelerin yapılarının belirli bir normal formda matematiksel bir tanımını vermek mümkündür. Bu fikirlerin gelişimi, yazarın hesaplanabilir fonksiyon tanımına ve hesaplanabilirliğin † etkin hesaplanabilirlik ile özdeşleştirilmesine yol açmaktadır...
- "† "Hesaplanabilir fonksiyon" ifadesini bir makine tarafından hesaplanabilir bir fonksiyon anlamında kullanacağız ve "etkin hesaplanabilir" ifadesinin bu tanımlardan herhangi biriyle özel olarak özdeşleştirilmeksizin sezgisel fikre atıfta bulunmasına izin vereceğiz". ⓘ
J.B. Rosser (1939) ve S.C. Kleene (1943)
J. Barkley Rosser 'etkin [matematiksel] yöntemi' aşağıdaki şekilde tanımlamıştır (italik yazım eklenmiştir):
- "'Etkin yöntem' burada, her adımı kesin olarak belirlenmiş ve sonlu sayıda adımda cevabı üreteceği kesin olan bir yöntemin oldukça özel anlamında kullanılmaktadır. Bu özel anlamla, bugüne kadar üç farklı kesin tanım verilmiştir. [dipnot #5; hemen aşağıdaki tartışmaya bakınız]. Bunlardan en basit olanı (Post ve Turing'e atfen), belirli problem kümelerini çözmek için etkili bir yöntemin, soruyu eklemek ve (daha sonra) cevabı okumak dışında herhangi bir insan müdahalesi olmadan kümedeki herhangi bir problemi çözecek bir makine inşa edilebiliyorsa var olduğunu söyler. Her üç tanım da eşdeğerdir, dolayısıyla hangisinin kullanıldığı önemli değildir. Dahası, üçünün de eşdeğer olması, herhangi birinin doğruluğu için çok güçlü bir argümandır." (Rosser 1939: 225-226) ⓘ
Rosser'ın dipnotu No. 5, (1) Church ve Kleene'nin çalışmalarına ve λ-tanımlanabilirlik tanımlarına, özellikle de Church'ün An Unsolvable Problem of Elementary Number Theory (1936) adlı çalışmasında bu tanımı kullanmasına atıfta bulunmaktadır; (2) Herbrand ve Gödel ve özellikle Gödel'in Principia Mathematica ve İlgili Sistemlerin Biçimsel Olarak Çözülemeyen Önermeleri Üzerine I (1931) adlı ünlü makalesinde kullandığı özyineleme kullanımı; ve (3) Post (1936) ve Turing'in (1936-37) hesaplama mekanizma-modelleri. ⓘ
Stephen C. Kleene, Church-Turing tezi olarak bilinen meşhur "Tez I" olarak tanımlamıştır. Ancak bunu aşağıdaki bağlamda yapmıştır (orijinalinde kalın harflerle yazılmıştır):
- "12. Algoritmik teoriler... Tam bir algoritmik teori kurarken yaptığımız şey, bağımsız değişkenlerin her bir değer kümesi için gerçekleştirilebilen, prosedürün zorunlu olarak sonlandığı ve sonuçtan "yüklem değeri doğru mu?" sorusuna "evet" veya "hayır" şeklinde kesin bir cevap okuyabileceğimiz bir prosedür tanımlamaktır." (Kleene 1943: 273) ⓘ
1950 Sonrası Tarih
"Algoritma" tanımının daha da iyileştirilmesine yönelik bir dizi çaba gösterilmiştir ve özellikle matematiğin temelleri (özellikle Church-Turing tezi) ve zihin felsefesi (özellikle yapay zeka hakkındaki tartışmalar) ile ilgili konular nedeniyle faaliyetler devam etmektedir. Daha fazlası için bkz. Algoritma tanımlamaları. ⓘ
Tarihi
Algoritma sözcüğü, Özbekistan'ın Harezm, bugünkü Türkmenistan'ın Hive kentinde doğmuş olan Ebu Abdullah Muhammed İbn Musa el Harezmi'den gelir. Bu alim 9. yüzyılda cebir alanındaki algoritmik çalışmalarını kitaba dökerek matematiğe çok büyük bir katkı sağlamıştır. "Hisab el-cebir ve el-mukabala (حساب الجبر و المقابلة)" kitabı dünyanın ilk cebir kitabı ve aynı zamanda ilk algoritma koleksiyonunu oluşturur. Latince çevirisi Avrupa'da çok ilgi görür. Alimin ismini telaffuz edemeyen Avrupalılar "algorizm" sözcüğünü "Arap sayıları kullanarak aritmetik problemler çözme kuralları" manasında kullanırlar. Bu sözcük daha sonra "algoritma"ya dönüşür ve genel kapsamda kullanılır. ⓘ
Uygulama
Çoğu algoritmalar bilgisayar olarak uygulanmak üzere tasarlanmıştır. Bununla birlikte, başka yöntemlerle de uygulanmaktadır, biyolojik sinir ağı (örneğin insan beyninin hesap yapması veya bir böceğin yemek araması), elektrik devresi veya mekanik cihazlar gibi. ⓘ
Bilgisayar algoritmasına örnek verelim. Kullanıcının girdiği dört sayının ortalamasını görüntüleyen algoritmayı yazalım:
A0 --> Başla
A1 --> Sayaç=0 (Sayaç'ın ilk sayısı 0 olarak başlar.)
A2 --> Sayı=? : T=T+Sayı (Sayıyı giriniz. T'ye sayıyı ekle ve T'yi göster.)
A3 --> Sayaç=Sayaç+1 (Sayaç'a 1 ekle ve sayacı göster.)
A4 --> Sayaç<4 ise A2'ye git. (Eğer sayaç 4'ten küçükse Adım 2'ye git.)
A5 --> O=T/4 (Ortalama için T değerini 4'e böl)
A6 --> O'yu göster. (Ortalamayı göster.)
A7 --> Dur ⓘ

İkinci dereceden ax² + bx + c = 0 biçiminde bir denklemin tüm köklerini bulmak için algoritma yazalım:
Adım 1: Başla. Adım 2: a, b, c, D, x1, x2, rp ve ip değişkenlerini tanımla. Adım 3: Diskriminant değerini hesapla. D ← b2-4ac Adım 4: Eğer D≥0 x1 ← (-b+√D) / 2a x2 ← (-b-√D) / 2a değerlerini hesapla ve x1,x2 değişkenleri göster. Eğer D≥0 değilse, Gerçek kısım(rp) ve sanal kısmını(ip) hesapla. rp ← b / 2a ip ← √ (D) / 2a Adım 5: "rp + j(ip)" ve "rp - j(ip)" değerlerini göster. Adım 6: Dur.
Kullanıcı tarafından girilen bir sayının faktöriyel değerini bulmak için bir algoritma yazalım:
Adım 1: Başla.
Adım 2: factorial,i ve n değişkenlerini tanımla.
Adım 3: Değişkenlerin başlangıç değerlerini tanımla.
factorial ← 1
i ← 1
Adım 4: Ekrandan girilen n değerini oku.
Adım 5: (i=n) eşitliği sağlanana kadar tekrarla.
5.1: factorial←factorial*i
5.2: i←i+1
Adım 6: factorial değişkeninin değerini göster.
Adım 7: Dur. ⓘ
Algoritmalara eleştirel yaklaşımlar
Algoritmaların kullanımı hayatın her alanında giderek yaygınlaşmaktadır. İş yerlerindeki performans değerlendirmelerinden bankaların kime kredi vereceğine, güvenlik sistemlerinden sosyal medya platformlarındaki önerilere kadar hayatın her alanında etkili olan algoritmalara özellikle de sosyal bilimci akademisyenler çeşitli eleştiriler yöneltmektedir. Algoritmaların teknolojik etkilerinin yanı sıra toplumsal bir güce de sahip oldukları, toplumsal gruplar arasındaki eşitsizlikleri derinleştirdikleri, yeni güç dengeleri oluşturdukları ve farklı otoriteler tarafından toplumun belli kesimlerini baskılamak için kullanıldıklarının altı çizilmektedir. ⓘ
