Uzayzaman
| Üzerine bir serinin parçası ⓘ |
| Uzayzaman |
|---|
 |
|
|
Fizikte uzayzaman, uzayın üç boyutunu ve zamanın bir boyutunu tek bir dört boyutlu manifoldda birleştiren matematiksel bir modeldir. Uzayzaman diyagramları, farklı gözlemcilerin olayların nerede ve ne zaman meydana geldiğini neden farklı algıladıkları gibi göreceli etkileri görselleştirmek için kullanılabilir. ⓘ
20. yüzyıla kadar evrenin üç boyutlu geometrisinin (koordinatlar, mesafeler ve yönler açısından uzamsal ifadesi) tek boyutlu zamandan bağımsız olduğu varsayılıyordu. Fizikçi Albert Einstein, görelilik teorisinin bir parçası olarak uzayzaman fikrinin geliştirilmesine yardımcı olmuştur. Einstein'ın öncü çalışmalarından önce, bilim insanlarının fiziksel olayları açıklamak için iki ayrı teorisi vardı: Isaac Newton'un fizik yasaları kütleli nesnelerin hareketini açıklarken, James Clerk Maxwell'in elektromanyetik modelleri ışığın özelliklerini açıklıyordu. Ancak 1905 yılında Einstein, özel görelilik üzerine yaptığı çalışmayı iki önermeye dayandırdı:
- Fizik yasaları tüm eylemsiz sistemlerde (yani hızlanmayan referans çerçevelerinde) değişmezdir (yani aynıdır)
- Boşluktaki ışık hızı, ışık kaynağının hareketinden bağımsız olarak tüm gözlemciler için aynıdır. ⓘ
Bu önermeleri bir araya getirmenin mantıksal sonucu, şimdiye kadar birbirinden bağımsız olduğu varsayılan dört boyutun (uzay ve zaman) ayrılmaz bir şekilde birleşmesidir. Mantığa aykırı birçok sonuç ortaya çıkar: ışık kaynağının hareketinden bağımsız olmasının yanı sıra, ışık hızı ölçüldüğü referans çerçevesinden bağımsız olarak sabittir; farklı eylemsiz referans çerçevelerinde ölçüldüğünde olay çiftlerinin mesafeleri ve hatta zamansal sıralamaları değişir (bu eşzamanlılığın göreliliğidir); ve hızların doğrusal toplanabilirliği artık geçerli değildir. ⓘ
Einstein teorisini kinematik (hareket eden cisimlerin incelenmesi) açısından çerçevelemiştir. Teorisi, Lorentz'in 1904 tarihli elektromanyetik fenomen teorisi ve Poincaré'nin elektrodinamik teorisi üzerinde bir ilerlemeydi. Bu teoriler Einstein'ın ortaya attığı denklemlerle (yani Lorentz dönüşümü) aynı denklemleri içermesine rağmen, esasen mevcut paradigmalara uyması son derece zor olan çeşitli deneylerin sonuçlarını (ünlü Michelson-Morley interferometre deneyi de dahil olmak üzere) açıklamak için önerilen geçici modellerdi. ⓘ
1908 yılında, genç Einstein'ın Zürih'teki matematik profesörlerinden biri olan Hermann Minkowski, özel göreliliğin zamanı ve uzayın üç uzamsal boyutunu şimdi Minkowski uzayı olarak bilinen dört boyutlu tek bir süreklilikte birleştiren geometrik bir yorumunu sundu. Bu yorumun önemli bir özelliği uzay-zaman aralığının resmi tanımıdır. Olaylar arasındaki mesafe ve zaman ölçümleri farklı referans çerçevelerinde yapılan ölçümler için farklılık gösterse de, uzay-zaman aralığı kaydedildikleri eylemsiz referans çerçevesinden bağımsızdır. ⓘ
Minkowski'nin göreliliğe getirdiği geometrik yorum, Einstein'ın 1915'te geliştirdiği ve kütle ile enerjinin düz uzayzamanı nasıl bir sözde-Riemann manifolduna dönüştürdüğünü gösterdiği genel görelilik kuramı için hayati önem taşıyordu. ⓘ

Uzayzaman, uzay ile zamanı "uzay-zaman sürekliliği" adı verilen yapıda birleştiren matematik modeli. Öklitçi yaklaşıma göre evren uzayın üç boyutu ve dördüncü boyutu oluşturan zamandan oluşur. Fizikçiler, uzay ve zaman kavramlarını tek bir çatı altında birleştirmek yoluyla, karmaşık fizik teorilerini önemli ölçüde basitleştirmeyi ve evrenin işleyişini süpergalaktik (fiziksel kozmoloji) ve altatomik (atom altı, bkz. kuantum fiziği) seviyelerde daha basit ve ortak bir dilde açıklamayı başarmışlardır. ⓘ
Klasik mekanikte, Öklid uzayı kullanımı, uzayzamanı kendine mal etmek yerine, zamanı gözlemcinin hareket durumundan bağımsız olarak evrensel ve değişmez gibi kabul edip ele alır. Göreliliğe dayalı bağlamda ise zaman, uzayın üç boyutundan ayrı olarak düşünülemez; çünkü bir cismin vektörel hızı, ışığın hızı ve bir de güçlü kütle çekimsel alanların gücü ile ilişkilidir. Bu kütle çekimsel alanlar zamanın ilerleyişini yavaşlatabilir ve bir o kadar da gözlemcinin hareket durumuna bağlıdır. Bu nedenle de evrensel değildir. ⓘ
Evrensel dediğimiz, bir olgunun evrenin her köşesinde doğru ve değişmez olmasıdır. Ancak Albert Einstein'ın kurduğu Görelilik Kuramı'na göre zaman evrenin her köşesinde aynı değildir ve gözlemciye göre değişir, görecelidir. Örneğin, kütle uzayzamanda eğrilikler yaratır. Burada zaman bükülür ve zaman bu eğride bulunan bir gözlemciye göre, dışarıda duran bir başka gözlemciye olandan daha yavaş akar. İşte burada zaman evrensel değildir. ⓘ
Bu bükülmeyi şu şekilde açıklayabiliriz: Düz bir yatak düşünün. Bu yatağın üzerine gergin bir çarşaf serin ve hiç kırışıklık olmasın. İşte bu dümdüz çarşaf iki boyutla tanımladığımız uzay-zaman düzlemi olsun. Şimdi bu düzleme bir gezegeni simgeleyen demir bir bilye koyun. Bilye yatağa biraz gömülüp bir göçük yaratarak çarşafı da bükecektir. İşte zaman da bu şekilde demir bilye ile simgelediğimiz kütle yardımıyla bükülebilir. Kütlenin artışı, bu kütlenin uzay-zaman düzlemini büküşünü arttırır. Kütle arttıkça göçük de artar. Eğer kütle ölçülemeyecek boyutlarda aşırı büyük olursa uzay-zaman düzlemi ışığı bile hapsedecek kadar göçecektir. İşte bu göçük kara delik olarak adlandırılır. Eğim çok olduğu için ışık karadelikten girer ama geri çıkmaz. Bazı teorilere göre bu içeri giren ışık evrenin başka bir noktasından geri çıkar. Bu teorilerde karadelikler dipsiz kuyular değillerdir, iki ucu açık bir boru gibi düşünülebilir. ⓘ
Giriş
Tanımlar
Rölativistik olmayan klasik mekanik, zamanı uzay boyunca tekdüze ve uzaydan ayrı evrensel bir ölçüm niceliği olarak ele alır. Klasik mekanik, zamanın gözlemcinin hareket durumundan ya da dışsal herhangi bir şeyden bağımsız olarak sabit bir geçiş hızına sahip olduğunu varsayar. Dahası, uzayın Öklidyen olduğunu varsayar; uzayın sağduyu geometrisini takip ettiğini varsayar. ⓘ
Özel görelilik bağlamında, zaman uzayın üç boyutundan ayrılamaz, çünkü bir nesne için zamanın geçtiği gözlemlenen hız, nesnenin gözlemciye göre hızına bağlıdır. Genel görelilik, yerçekimi alanlarının, alanın dışındaki bir gözlemci tarafından görülen bir nesne için zamanın geçişini nasıl yavaşlatabileceğine dair bir açıklama da sağlar. ⓘ
Sıradan uzayda bir konum, boyutlar olarak bilinen üç sayı ile belirtilir. Kartezyen koordinat sisteminde bunlar x, y ve z olarak adlandırılır. Uzayzamandaki bir konum olay olarak adlandırılır ve dört sayının belirtilmesini gerektirir: uzaydaki üç boyutlu konum, artı zamandaki konum (Şekil 1). Bir olay x, y, z ve t koordinatları ile temsil edilir. Uzay-zaman böylece dört boyutludur. Matematiksel olaylar sıfır süreye sahiptir ve uzay-zamanda tek bir noktayı temsil eder. ⓘ
Bir parçacığın uzay-zaman boyunca izlediği yol, olayların art arda sıralanması olarak düşünülebilir. Olaylar dizisi, bir parçacığın uzay-zaman boyunca ilerleyişini temsil eden bir çizgi oluşturmak üzere birbirine bağlanabilir. Bu çizgiye parçacığın dünya çizgisi denir. ⓘ
Matematiksel olarak uzayzaman bir manifolddur, yani yeterince küçük ölçeklerde bir kürenin düz görünmesi gibi her noktanın yakınında yerel olarak "düz" görünür. Son derece büyük bir ölçek faktörü, (geleneksel olarak ışık hızı olarak adlandırılır) uzayda ölçülen mesafeleri zamanda ölçülen mesafelerle ilişkilendirir. Bu ölçek faktörünün büyüklüğü (uzayda yaklaşık 300.000 kilometre veya 190.000 mil, zamanda bir saniyeye eşittir), uzayzamanın bir manifold olduğu gerçeğiyle birlikte, sıradan, rölativistik olmayan hızlarda ve sıradan, insan ölçeğindeki mesafelerde, insanların gözlemleyebileceği, dünya Öklidyen olsaydı gözlemleyebileceklerinden belirgin şekilde farklı olan çok az şey olduğunu ima eder. Ancak 1800'lerin ortalarında Fizeau deneyi ve Michelson-Morley deneyi gibi hassas bilimsel ölçümlerin ortaya çıkmasıyla birlikte, Öklid uzayının örtük varsayımına dayanan tahminlerle gözlemler arasında şaşırtıcı tutarsızlıklar fark edilmeye başlanmıştır. ⓘ

Özel görelilikte gözlemci, çoğu durumda, bir dizi nesne veya olayın ölçüldüğü bir referans çerçevesi anlamına gelir. Bu kullanım, terimin sıradan İngilizce anlamından önemli ölçüde farklıdır. Referans çerçeveleri doğası gereği yerel olmayan yapılardır ve terimin bu kullanımına göre, bir gözlemcinin bir konuma sahip olduğundan bahsetmek mantıklı değildir. Şekil 1-1'de, söz konusu çerçevenin, bu referans çerçevesi içinde senkronize edilmiş ve uzayın üç boyutu boyunca sonsuza kadar uzanan yoğun bir saat kafesiyle donatıldığını düşünün. Kafes içindeki herhangi bir özel konum önemli değildir. Saatlerden oluşan kafes, tüm çerçeve içinde gerçekleşen olayların zamanını ve konumunu belirlemek için kullanılır. Gözlemci terimi, bir eylemsiz referans çerçevesiyle ilişkili tüm saat topluluğunu ifade eder. Bu idealleştirilmiş durumda, uzaydaki her noktanın kendisiyle ilişkili bir saati vardır ve böylece saatler her olayı anında kaydeder, bir olay ile kaydı arasında zaman gecikmesi olmaz. Ancak gerçek bir gözlemci, ışık hızı nedeniyle bir sinyalin yayılması ile algılanması arasında bir gecikme görecektir. Saatleri senkronize etmek için, bir deneyi takip eden veri indirgemesinde, bir sinyalin alındığı zaman, idealize edilmiş bir saat kafesi tarafından kaydedilmiş olması halinde gerçek zamanını yansıtacak şekilde düzeltilecektir. ⓘ
Özel görelilik üzerine yazılmış birçok kitapta, özellikle de daha eski olanlarda, "gözlemci" kelimesi kelimenin daha sıradan anlamında kullanılmaktadır. Hangi anlamın benimsendiği genellikle bağlamdan anlaşılır. ⓘ
Fizikçiler bir kişinin ölçtüğü ya da gözlemlediği şey (sinyal yayılım gecikmeleri hesaba katıldıktan sonra) ile bu tür düzeltmeler olmaksızın görsel olarak gördüğü şey arasında ayrım yaparlar. Kişinin ölçtüğü/gözlemlediği ile gördüğü arasındaki farkı anlayamaması, göreliliğin yeni öğrencileri arasında pek çok hatanın kaynağıdır. ⓘ
Tarih
1800'lerin ortalarına gelindiğinde, Arago lekesinin gözlemlenmesi ve ışığın havadaki ve sudaki hızının farklı ölçümleri gibi çeşitli deneylerin, korpüsküler bir teorinin aksine ışığın dalga doğasını kanıtladığı düşünülüyordu. Dalgaların yayılması için dalgalı bir ortamın var olması gerektiği varsayılmıştır; ışık dalgaları söz konusu olduğunda bu ortamın varsayımsal bir ışıklı eter olduğu düşünülmüştür. Ancak, bu varsayımsal ortamın özelliklerini belirlemeye yönelik çeşitli girişimler çelişkili sonuçlar vermiştir. Örneğin, 1851 Fizeau deneyi, akan sudaki ışık hızının, havadaki ışık hızı ile suyun hızının toplamından, suyun kırılma indeksine bağlı bir miktar daha az olduğunu göstermiştir. Diğer sorunların yanı sıra, bu deneyin ima ettiği kısmi eter sürüklenmesinin kırılma indisine (ki bu da dalga boyuna bağlıdır) bağlı olması, eterin aynı anda farklı ışık renkleri için farklı hızlarda aktığı gibi tatsız bir sonuca yol açmıştır. 1887'deki ünlü Michelson-Morley deneyi (Şekil 1-2), Dünya'nın varsayımsal ether boyunca hareketinin ışık hızı üzerinde farklı bir etkisi olmadığını gösterdi ve en olası açıklama olan tam ether sürüklenmesi, yıldız sapması gözlemiyle çelişiyordu. ⓘ
1889'da George Francis FitzGerald ve 1892'de Hendrik Lorentz, bağımsız olarak, sabit eter boyunca seyahat eden maddi cisimlerin geçişlerinden fiziksel olarak etkilendiklerini, hareket yönünde Michelson-Morley deneyinin olumsuz sonuçlarını açıklamak için tam olarak gerekli olan miktarda büzüldüklerini öne sürdüler. (Hareket yönüne çapraz yönlerde hiçbir uzunluk değişikliği meydana gelmez). ⓘ
1904 yılına gelindiğinde Lorentz teorisini öyle genişletmişti ki, Einstein'ın daha sonra türeteceği denklemlerle (yani Lorentz dönüşümü) biçimsel olarak özdeş, ancak temelde farklı bir yoruma sahip denklemlere ulaşmıştı. Bir dinamik teorisi (kuvvetlerin ve torkların incelenmesi ve bunların hareket üzerindeki etkileri) olarak teorisi, maddenin fiziksel bileşenlerinin gerçek fiziksel deformasyonlarını varsayıyordu. Lorentz'in denklemleri, yerel zaman adını verdiği ve ışığın sapmasını, Fizeau deneyini ve diğer fenomenleri açıklayabileceği bir nicelik öngörüyordu. Ancak Lorentz yerel zamanı yalnızca yardımcı bir matematiksel araç, bir sistemden diğerine dönüşümü basitleştiren bir hile olarak görüyordu. ⓘ
Yüzyılın başında diğer fizikçiler ve matematikçiler şu anda uzayzaman olarak bilinen şeye ulaşmaya çok yaklaştılar. Einstein'ın kendisi, bulmacanın ayrı parçalarını çözen bu kadar çok insan varken, "özel görelilik kuramının, gelişimini geçmişe bakarak değerlendirirsek, 1905'te keşif için olgunlaştığını" belirtmiştir. ⓘ
Önemli bir örnek, 1898'de iki olayın eşzamanlılığının bir konvansiyon meselesi olduğunu savunan Henri Poincaré'dir. 1900 yılında, Lorentz'in "yerel zamanının" aslında hareketli saatler tarafından gösterilen şey olduğunu, sabit ışık hızı varsayımıyla saat senkronizasyonunun açıkça operasyonel bir tanımını uygulayarak kabul etmiştir. 1900 ve 1904'te, görelilik ilkesi olarak adlandırdığı ilkenin geçerliliğini vurgulayarak eterin doğal olarak tespit edilemezliğini öne sürdü ve 1905/1906'da Lorentz'in elektron teorisini görelilik postülasına uygun hale getirmek için matematiksel olarak mükemmelleştirdi. Lorentz değişmez kütle çekimi üzerine çeşitli hipotezleri tartışırken, dört-konum, dört-hız ve dört-kuvvet olmak üzere çeşitli dört vektör tanımlayarak yenilikçi 4-boyutlu uzayzaman kavramını ortaya attı. Ancak daha sonraki çalışmalarında 4-boyutlu formalizmin peşine düşmemiş, bu araştırma çizgisinin "sınırlı kâr için büyük acılar gerektirdiğini" belirtmiş ve sonuçta "dünyamızın tanımlanması için en uygun dilin üç-boyutlu dil olduğu" sonucuna varmıştır. Dahası, 1909 gibi geç bir tarihte bile Poincaré Lorentz dönüşümünün dinamik yorumuna inanmaya devam etmiştir. Bu ve diğer nedenlerden dolayı, çoğu bilim tarihçisi Poincaré'nin bugün özel görelilik olarak adlandırılan şeyi icat etmediğini savunmaktadır. ⓘ
Einstein 1905 yılında özel göreliliği (uzay-zaman formalizminin tekniklerini kullanmadan da olsa) modern anlamda bir uzay ve zaman teorisi olarak tanıtmıştır. Elde ettiği sonuçlar matematiksel olarak Lorentz ve Poincaré'ninkilere eşdeğer olmakla birlikte, Einstein Lorentz dönüşümlerinin madde ve eter arasındaki etkileşimlerin sonucu olmadığını, daha ziyade uzay ve zamanın doğasıyla ilgili olduğunu göstermiştir. Tüm sonuçlarını, tüm teorinin iki varsayım üzerine inşa edilebileceğini kabul ederek elde etti: Görelilik ilkesi ve ışık hızının sabitliği ilkesi. ⓘ
Einstein analizini dinamikten ziyade kinematik (kuvvetlere atıfta bulunmadan hareket eden cisimlerin incelenmesi) açısından gerçekleştirdi. Konuyu tanıtan çalışmaları, hareket halindeki saatler arasında ışık sinyallerinin değiş tokuşunu, hareketli çubukların uzunluklarının dikkatli ölçümlerini ve benzeri diğer örnekleri içeren canlı imgelerle doluydu. ⓘ
Buna ek olarak, Einstein 1905'te kütle ve enerjinin genel eşdeğerliğini ortaya koyarak elektromanyetik kütle-enerji ilişkisine dair önceki girişimlerin yerini almış, bu da 1907'de eylemsiz ve kütleçekimsel kütlenin eşdeğerliğini ilan eden eşdeğerlik ilkesini formüle etmesinde etkili olmuştur. Einstein, kütle-enerji eşdeğerliğini kullanarak, bir cismin kütleçekimsel kütlesinin enerji içeriğiyle orantılı olduğunu göstermiştir ki bu da genel göreliliğin geliştirilmesindeki ilk sonuçlardan biridir. Başlangıçta uzayzaman hakkında geometrik olarak düşünmemiş gibi görünse de, genel göreliliğin daha sonraki gelişiminde Einstein uzayzaman formalizmini tamamen dahil etmiştir. ⓘ
Einstein 1905'te kitabını yayınladığında, bir başka rakibi olan eski matematik profesörü Hermann Minkowski de özel göreliliğin temel unsurlarının çoğuna ulaşmıştı. Max Born, Minkowski'nin öğrencisi/iş ortağı olmak için Minkowski ile yaptığı bir görüşmeyi anlattı:
Köln'e gittim, Minkowski ile tanıştım ve onun 2 Eylül 1908'de verdiği ünlü 'Uzay ve Zaman' dersini dinledim. [Einstein'ın, birbirlerine göre hareket eden gözlemcilerin farklı yerel zamanlarının eşdeğerliğini açıkladığı makalesini yayınladığında büyük bir şok yaşadığını söyledi; çünkü kendisi de aynı sonuçlara bağımsız olarak ulaşmış ama bunları yayınlamamıştı çünkü önce matematiksel yapıyı tüm ihtişamıyla çözmek istiyordu. Hiçbir zaman bir öncelik iddiasında bulunmadı ve Einstein'a bu büyük keşifte her zaman tam pay verdi. ⓘ
Minkowski, Michelson'un yıkıcı deneylerinden sonra elektrodinamiğin durumuyla en azından Minkowski ve David Hilbert'in Lorentz, Poincaré ve diğerlerinin makalelerini incelemek üzere dönemin önemli fizikçilerinin katıldığı ileri düzey bir semineri yönettikleri 1905 yazından beri ilgileniyordu. Bununla birlikte, Minkowski'nin kendi adını taşıyacak olan özel göreliliğin geometrik formülasyonunu ne zaman formüle etmeye başladığı veya Poincaré'nin Lorentz dönüşümünün dört boyutlu yorumundan ne ölçüde etkilendiği hiç açık değildir. Einstein'ın Lorentz dönüşümlerinin anlaşılmasına yaptığı kritik katkıyı tam olarak takdir edip etmediği, Einstein'ın çalışmasını Lorentz'in çalışmasının bir uzantısı olarak düşünüp düşünmediği de açık değildir. ⓘ
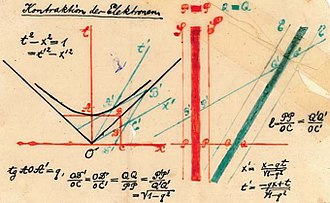
Minkowski, 5 Kasım 1907'de (ölümünden bir yıldan biraz daha uzun bir süre önce) Göttingen Matematik Topluluğu'na verdiği "Görelilik İlkesi" (Das Relativitätsprinzip) başlıklı bir konferansta uzayzamanın geometrik yorumunu tanıttı. 21 Eylül 1908'de Minkowski, Alman Bilim Adamları ve Hekimler Derneği'ne Uzay ve Zaman (Raum und Zeit) başlıklı ünlü konuşmasını sundu. Uzay ve Zaman'ın açılış sözleri Minkowski'nin ünlü "Bundan böyle, kendisi için uzay ve kendisi için zaman tamamen bir gölgeye indirgenecek ve yalnızca ikisinin bir tür birliği bağımsızlığını koruyacaktır" ifadesini içerir. Uzay ve Zaman, uzay-zaman diyagramlarının (Şekil 1-4) ilk halka açık sunumunu içeriyordu ve ışık hızının sonlu olduğuna dair deneysel gözlemle birlikte değişmez aralık kavramının (aşağıda ele alınmaktadır) özel göreliliğin tamamının türetilmesine izin verdiğinin dikkate değer bir gösterimini içeriyordu. ⓘ
Uzayzaman kavramı ve Lorentz grubu, uzayzaman aralığına benzer değişmez aralıkların kullanıldığı 19. yüzyılda geliştirilmiş olan belirli küre, hiperbolik veya konformal geometri türleri ve bunların dönüşüm gruplarıyla yakından bağlantılıdır. ⓘ
Einstein ise başlangıçta Minkowski'nin özel göreliliğe ilişkin geometrik yorumunu überflüssige Gelehrsamkeit (gereksiz öğrenilmişlik) olarak değerlendirerek küçümsemiştir. Bununla birlikte, 1907'de başlayan genel görelilik arayışını tamamlamak için göreliliğin geometrik yorumunun hayati önem taşıdığı kanıtlandı ve 1916'da Einstein, yorumu genel göreliliğe geçişi büyük ölçüde kolaylaştıran Minkowski'ye olan borcunu tamamen kabul etti. Genel göreliliğin eğri uzayzamanı gibi başka uzayzaman türleri de olduğundan, özel göreliliğin uzayzamanı bugün Minkowski uzayzamanı olarak bilinmektedir. ⓘ
Özel görelilikte uzayzaman
Uzayzaman aralığı
Üç boyutta, mesafe İki nokta arasındaki mesafe Pisagor teoremi kullanılarak tanımlanabilir:
İki izleyici iki noktanın x, y ve z konumlarını farklı koordinat sistemleri kullanarak ölçebilse de, noktalar arasındaki mesafe her ikisi için de aynı olacaktır (aynı birimleri kullanarak ölçüm yaptıkları varsayılırsa). Mesafe "değişmez "dir. ⓘ
Ancak özel görelilikte, iki nokta arasındaki mesafe, gözlemcilerden biri hareket ederken iki farklı gözlemci tarafından ölçüldüğünde Lorentz daralması nedeniyle artık aynı değildir. Eğer iki nokta uzayda olduğu kadar zamanda da birbirinden ayrılmışsa durum daha da karmaşıklaşır. Örneğin, bir gözlemci iki olayın aynı yerde, ancak farklı zamanlarda meydana geldiğini görürse, ilk gözlemciye göre hareket eden bir kişi iki olayın farklı yerlerde meydana geldiğini görecektir, çünkü (kendi bakış açısından) sabittir ve olayın konumu uzaklaşmakta ya da yaklaşmaktadır. Dolayısıyla, iki olay arasındaki etkin "mesafeyi" ölçmek için farklı bir ölçü kullanılmalıdır. ⓘ
Dört boyutlu uzayzamanda, mesafenin benzeri aralıktır. Zaman dördüncü bir boyut olarak devreye girse de, uzaysal boyutlardan farklı bir şekilde ele alınır. Dolayısıyla Minkowski uzayı dört boyutlu Öklid uzayından önemli açılardan farklılık gösterir. Uzay ve zamanı uzayzamanda birleştirmenin temel nedeni, uzay ve zamanın ayrı ayrı değişmez olmamasıdır; yani, uygun koşullar altında, farklı gözlemciler iki olay arasındaki zamanın uzunluğu (zaman genişlemesi nedeniyle) veya iki olay arasındaki mesafe (uzunluk daralması nedeniyle) konusunda anlaşmazlığa düşeceklerdir. Ancak özel görelilik, uzaydaki ve zamandaki mesafeleri birleştiren uzay-zaman aralığı adı verilen yeni bir değişmez sağlar. Herhangi iki olay arasındaki zaman ve mesafeyi ölçen tüm gözlemciler aynı uzay-zaman aralığını hesaplayacaktır. Bir gözlemcinin iki olay arasındaki zaman farkını şu şekilde ölçtüğünü varsayalım ve bir uzamsal mesafe O zaman uzayzaman aralığı bir mesafe ile ayrılmış iki olay arasında uzayda ve içinde -koordinattır:
veya üç uzay boyutu için, ⓘ
Sabit ışık hızı, zaman birimlerini (saniye gibi) uzay birimlerine (metre gibi) dönüştürür. Kareli aralık A ve B olayları arasındaki ayrımın bir ölçüsüdür; bu olaylar ya iki ayrı nesne tarafından gerçekleştirildiği için ya da uzaydaki tek bir nesne olayları arasında eylemsiz olarak hareket ettiği için zaman ve ek olarak uzay olarak ayrılmıştır. Ayırma aralığı, B olayını A olayından ayıran uzaysal mesafenin karesinin alınması ve aynı zaman aralığında bir ışık sinyali tarafından kat edilen uzaysal mesafenin karesinden çıkarılmasıyla elde edilir . Eğer olay ayrımı bir ışık sinyalinden kaynaklanıyorsa, bu fark ortadan kalkar ve . ⓘ
Dikkate alınan olaylar birbirine sonsuz derecede yakın olduğunda, şunları yazabiliriz ⓘ
Farklı bir eylemsizlik çerçevesinde, diyelim ki koordinatlarla uzayzaman aralığını yukarıdaki ile aynı biçimde yazılabilir. Işık hızının sabitliği nedeniyle, tüm eylemsiz çerçevelerdeki ışık olayları sıfır aralığa aittir, . Başka herhangi bir sonsuz küçük olay için kanıtlanabilir ki Bu da entegrasyon sonucunda . Tüm referans çerçeveleri arasındaki herhangi bir olayın aralığının değişmezliği, özel görelilik teorisinin temel sonuçlarından biridir. ⓘ
Kısalık için, aşağıdaki tartışmanın çoğu da dahil olmak üzere, sık sık aralık ifadelerinin delta olmadan ifade edildiği görülse de, genel olarak anlaşılmalıdır, anlamına gelir vb. Biz her zaman şunlarla ilgileniyoruz farklılıklar İki olaya ait uzamsal veya zamansal koordinat değerlerinin ve tercih edilen bir orijin olmadığından, tek koordinat değerlerinin temel bir anlamı yoktur. ⓘ

Yukarıdaki denklem Pisagor teoremine benzer, ancak denklemin iki ucu arasında bir eksi işareti vardır. ve terimlerdir. Uzayzaman aralığı şu niceliktir değil kendisi. Bunun nedeni, Öklid geometrisindeki mesafelerin aksine, Minkowski uzayzamanındaki aralıkların negatif olabilmesidir. Negatif sayıların karekökleriyle uğraşmak yerine, fizikçiler geleneksel olarak Bir şeyin karesinden ziyade, kendi içinde ayrı bir sembol olarak. ⓘ
Genel olarak gerçek sayının herhangi bir değerini alabilir. Eğer pozitif ise, uzay-zaman aralığı zaman benzeri olarak adlandırılır. Herhangi bir kütleli cismin kat ettiği uzaysal mesafe her zaman ışığın aynı zaman aralığında kat ettiği mesafeden daha az olduğundan, gerçek aralıklar her zaman zamana benzerdir. Eğer negatifse, uzayzaman aralığının uzay benzeri olduğu söylenir, burada uzayzaman aralığı hayali olur. Uzayzaman aralıkları şu durumlarda sıfıra eşittir Başka bir deyişle, ışık hızında hareket eden bir şeyin dünya çizgisi üzerindeki iki olay arasındaki uzay-zaman aralığı sıfırdır. Böyle bir aralık ışık benzeri ya da sıfır olarak adlandırılır. Uzak bir yıldızdan gözümüze ulaşan bir foton, (bizim bakış açımıza göre) geçişi sırasında yıllar geçirmiş olmasına rağmen yaşlanmayacaktır. ⓘ
Bir uzay-zaman diyagramı tipik olarak yalnızca tek bir uzay ve tek bir zaman koordinatıyla çizilir. Şekil 2-1, aynı olaydan kaynaklanan ve zıt yönlere giden iki fotonun, A ve B, dünya çizgilerini (yani uzayzamandaki yollarını) gösteren bir uzayzaman diyagramı sunmaktadır. Buna ek olarak, C ışık hızından daha yavaş bir nesnenin dünya çizgisini göstermektedir. Dikey zaman koordinatı şu şekilde ölçeklendirilmiştir Böylece yatay uzay koordinatıyla aynı birimlere (metre) sahip olur. Fotonlar ışık hızında hareket ettiğinden, dünya çizgilerinin eğimi ±1'dir. Başka bir deyişle, bir fotonun sağa veya sola gittiği her metre yaklaşık 3,3 nanosaniye zaman gerektirir. ⓘ
Görelilik literatüründe kullanılan iki işaret konvansiyonu vardır:
ve
Bu işaret konvansiyonları (+---) ve (-+++) metrik imzalarıyla ilişkilidir. Küçük bir değişiklik, zaman koordinatının ilk yerine son olarak yerleştirilmesidir. Her iki konvansiyon da çalışma alanında yaygın olarak kullanılmaktadır. ⓘ
Referans çerçeveleri


Farklı referans çerçevelerindeki gözlemciler tarafından ölçülen uzay-zaman koordinatlarının birbirleriyle nasıl karşılaştırıldığı hakkında fikir edinmek için, çerçevelerin standart bir konfigürasyonda olduğu basitleştirilmiş bir kurulumla çalışmak yararlıdır. Dikkatli olunursa bu, ulaşılan sonuçlarda genellik kaybı olmadan matematiğin basitleştirilmesine olanak tanır. Şekil 2-2'de iki Galile referans çerçevesi (yani geleneksel 3 uzay çerçeveleri) göreli hareket halinde gösterilmektedir. S çerçevesi birinci gözlemci O'ya, S′ ("S asal" olarak okunur) çerçevesi ise ikinci gözlemci O′'ya aittir.
- S çerçevesinin x, y, z eksenleri S′ çerçevesinin ilgili asal eksenlerine paralel olarak yönlendirilmiştir.
- S′ çerçevesi S çerçevesinin x yönünde, S çerçevesinden ölçülen sabit bir v hızıyla hareket eder.
- S ve S′ çerçevelerinin orijinleri, S çerçevesi için t = 0 ve S′ çerçevesi için t′ = 0 olduğunda çakışır. ⓘ
Şekil 2-3a, Şekil 2-2'yi farklı bir yönde yeniden çizmektedir. Şekil 2-3b, O gözlemcisinin bakış açısından bir uzay-zaman diyagramını göstermektedir. S ve S′ standart konfigürasyonda olduğundan, orijinleri S çerçevesi için t = 0 ve S′ çerçevesi için t′ = 0 zamanlarında çakışmaktadır. Ct′ ekseni, S′ çerçevesindeki x′ = 0 olan olaylardan geçer. Ancak x′ = 0 olan noktalar, S çerçevesinin x yönünde v hızıyla hareket eder, böylece sıfır dışında herhangi bir zamanda ct ekseniyle çakışmazlar. Bu nedenle, ct′ ekseni ct eksenine göre θ ile verilen bir açı ile eğilir ⓘ
x′ ekseni de x eksenine göre eğiktir. Bu eğimin açısını belirlemek için, bir ışık darbesinin dünya çizgisinin eğiminin her zaman ±1 olduğunu hatırlayalım. Şekil 2-3c, O′ gözlemcisinin bakış açısından bir uzayzaman diyagramı sunmaktadır. P olayı x′ = 0, ct′ = -a'da bir ışık atımının yayılmasını temsil etmektedir. Darbe, ışık kaynağından a uzaklıkta bulunan bir aynadan yansır (Q olayı) ve x′ = 0, ct′ = a'da ışık kaynağına geri döner (R olayı). ⓘ
Aynı P, Q, R olayları Şekil 2-3b'de O gözlemcisinin çerçevesinde çizilmiştir. Işık yollarının eğimleri = 1 ve -1'dir, böylece △PQR, PQ ve QR'nin her ikisi de x ve ct eksenlerine 45 derece olan bir dik üçgen oluşturur. OP = OQ = OR olduğundan, x′ ile x arasındaki açı da θ olmalıdır. ⓘ
Durağan çerçeve dik açılarda buluşan uzay ve zaman eksenlerine sahipken, hareketli çerçeve dar bir açıda buluşan eksenlerle çizilir. Çerçeveler aslında eşdeğerdir. Asimetri, uzay-zaman koordinatlarının Kartezyen bir düzlemde nasıl eşlenebileceği konusundaki kaçınılmaz çarpıklıklardan kaynaklanmaktadır ve Dünya'nın bir Merkatör projeksiyonunda, kutuplara yakın kara kütlelerinin (Grönland ve Antarktika) göreceli boyutlarının Ekvator'a yakın kara kütlelerine göre oldukça abartılı olmasından daha garip görülmemelidir. ⓘ
Işık konisi

Şekil 2-4'te O olayı bir uzay-zaman diyagramının orijinindedir ve iki köşegen çizgi orijin olayına göre sıfır uzay-zaman aralığına sahip tüm olayları temsil etmektedir. Bu iki çizgi O olayının ışık konisi olarak adlandırılan şeyi oluşturur, çünkü ikinci bir uzaysal boyut eklendiğinde (Şekil 2-5) O'da tepe noktalarıyla buluşan iki dik dairesel koni görünümü ortaya çıkar. Konilerden biri geleceğe (t>0), diğeri geçmişe (t<0) uzanır. ⓘ

Bir ışık (çift) konisi uzayzamanı tepe noktasına göre ayrı bölgelere ayırır. Gelecek ışık konisinin içi, tepe noktasından uzaysal mesafelerini ışık hızında geçmek için gerekenden daha fazla zamanla (zamansal mesafe) ayrılan tüm olaylardan oluşur; bu olaylar O olayının zamansal geleceğini oluşturur. Aynı şekilde, zamansal geçmiş de geçmiş ışık konisinin iç olaylarını oluşturur. Dolayısıyla, zamansal aralıklarda Δct, Δx'den büyüktür ve zamansal aralıkları pozitif yapar. Işık konisinin dışındaki bölge, O olayından, verilen zamanda ışık hızıyla geçilebileceğinden daha fazla alanla ayrılan olaylardan oluşur. Bu olaylar O olayının uzay benzeri bölgesi olarak adlandırılan ve Şekil 2-4'te "Başka Yerde" olarak gösterilen bölgeyi oluşturur. Işık konisi üzerindeki olayların O'dan ışık benzeri (veya boş ayrılmış) olduğu söylenir. Uzayzaman aralığının değişmezliği nedeniyle, tüm gözlemciler verilen herhangi bir olaya aynı ışık konisini atayacak ve böylece uzayzamanın bu bölünmesi üzerinde anlaşacaklardır. ⓘ
Işık konisi nedensellik kavramı içinde önemli bir role sahiptir. Işık hızından daha hızlı olmayan bir sinyalin O'nun konum ve zamanından D'nin konum ve zamanına gitmesi mümkündür (Şekil 2-4). Dolayısıyla O olayının D olayı üzerinde nedensel bir etkisi olması mümkündür. Gelecek ışık konisi O tarafından nedensel olarak etkilenebilecek tüm olayları içerir. Buna karşılık, sinyallerin ışık hızından daha hızlı hareket edemeyeceğini varsayarsak, uzay benzeri bölgede (Başka bir yerde) bulunan B veya C gibi herhangi bir olay ne O olayını etkileyebilir ne de O olayı tarafından böyle bir sinyal kullanılarak etkilenebilir. Bu varsayım altında, O olayı ile bir ışık konisinin uzay benzeri bölgesindeki herhangi bir olay arasındaki herhangi bir nedensel ilişki dışlanır. ⓘ
Eşzamanlılığın göreliliği

Tüm gözlemciler, verilen herhangi bir olay için, verilen olayın gelecek ışık konisi içindeki bir olayın verilen olaydan sonra meydana geldiği konusunda hemfikir olacaktır. Aynı şekilde, verilen herhangi bir olay için, verilen olayın geçmiş ışık konisi içindeki bir olay, verilen olaydan önce meydana gelir. Zamansal olarak ayrılmış olaylar için gözlemlenen önce-sonra ilişkisi, gözlemcinin referans çerçevesi ne olursa olsun, yani gözlemci nasıl hareket ediyor olursa olsun değişmeden kalır. Uzaya benzer şekilde ayrılmış olaylar için durum oldukça farklıdır. Şekil 2-4 v = 0 hızında hareket eden bir gözlemcinin referans çerçevesinden çizilmiştir. Bu referans çerçevesinden bakıldığında, C olayının O olayından sonra, B olayının ise O olayından önce gerçekleştiği görülmektedir. Farklı bir referans çerçevesinden bakıldığında, nedensel olarak ilişkili olmayan bu olayların sıralaması tersine çevrilebilir. Özellikle, iki olay belirli bir referans çerçevesinde eşzamanlı ise, bunların zorunlu olarak uzay benzeri bir aralıkla ayrıldıkları ve dolayısıyla nedensel olarak ilişkili olmadıkları not edilir. Eşzamanlılığın mutlak olmadığı, ancak gözlemcinin referans çerçevesine bağlı olduğu gözlemine eşzamanlılığın göreliliği adı verilir. ⓘ
Şekil 2-6, eşzamanlılığın göreliliğinin analizinde uzayzaman diyagramlarının kullanımını göstermektedir. Uzayzamandaki olaylar değişmezdir, ancak koordinat çerçeveleri yukarıda Şekil 2-3 için tartışıldığı gibi dönüşür. Üç olay (A, B, C) v = 0 hızında hareket eden bir gözlemcinin referans çerçevesinden bakıldığında eşzamanlıdır. v = 0.3c hızında hareket eden bir gözlemcinin referans çerçevesinden bakıldığında olaylar C, B, A sıralamasıyla gerçekleşiyor gibi görünür. v = -0.5c hızında hareket eden bir gözlemcinin referans çerçevesinden bakıldığında olaylar A, B, C sıralamasıyla gerçekleşiyor gibi görünür. Beyaz çizgi, gözlemcinin geçmişinden geleceğine doğru hareket eden ve üzerinde bulunan olayları vurgulayan bir eşzamanlılık düzlemini temsil eder. Gri alan gözlemcinin ışık konisidir ve değişmez kalır. ⓘ
Uzaya benzer bir uzayzaman aralığı, ölçülen olaylar gözlemci için eşzamanlı olsaydı gözlemcinin ölçeceği mesafenin aynısını verir. Uzaya benzer bir uzayzaman aralığı bu nedenle uygun mesafenin bir ölçüsünü sağlar, yani gerçek mesafe = Aynı şekilde, zamana benzer bir uzay-zaman aralığı, belirli bir dünya çizgisi boyunca hareket eden bir saatin kümülatif tik taklarının sunacağı zaman ölçüsünün aynısını verir. Zamana benzer bir uzayzaman aralığı bu nedenle uygun zamanın bir ölçüsünü sağlar = ⓘ
Değişmez hiperbol

Öklid uzayında (sadece uzaysal boyutlara sahip), bir noktadan eşit uzaklıktaki (Öklid metriği kullanılarak) noktalar kümesi bir daire (iki boyutta) veya bir küre (üç boyutta) oluşturur. (1+1)-boyutlu Minkowski uzayzamanında (bir zamansal ve bir uzamsal boyuta sahip), orijinden uzaktaki bazı sabit uzayzaman aralıklarındaki noktalar (Minkowski metriğini kullanarak) iki denklem tarafından verilen eğrileri oluşturur ⓘ
ile bazı pozitif reel sabitler. Bu denklemler x-ct uzay-zaman diyagramında değişmez hiperboller olarak adlandırılan iki hiperbol ailesini tanımlar. ⓘ
Şekil 2-7a'da, her bir eflatun hiperbol orijinden sabit bir uzay-zaman uzaklığına sahip tüm olayları birbirine bağlarken, yeşil hiperboller eşit zaman-zaman uzaklığına sahip olayları birbirine bağlamaktadır. ⓘ
X eksenini kesen eflatun hiperboller zamansal eğrilerdir, yani bu hiperboller uzayzamanda (sürekli hızlanan) parçacıklar tarafından kat edilebilecek gerçek yolları temsil etmektedir: Bir hiperbol üzerindeki herhangi iki olay arasında bir nedensellik ilişkisi mümkündür, çünkü tüm sekantlar için gerekli hızı temsil eden eğimin tersi . Öte yandan, ct eksenini kesen yeşil hiperboller uzay benzeri eğrilerdir çünkü bu hiperboller boyunca tüm aralıklar uzay benzeri aralıklardır: Bu hiperbollerden biri üzerindeki herhangi iki nokta arasında nedensellik mümkün değildir, çünkü tüm sekantlar . ⓘ
Şekil 2-7b (1+2)-boyutlu Minkowski uzayzamanındaki (bir zamansal ve iki uzamsal boyut) durumu karşılık gelen hiperboloidlerle yansıtmaktadır. Orijinden itibaren uzay benzeri aralıklarla yer değiştiren değişmez hiperboller bir tabakanın hiperboloidlerini oluştururken, orijinden itibaren zaman benzeri aralıklarla yer değiştiren değişmez hiperboller iki tabakanın hiperboloidlerini oluşturur. ⓘ
Orijine sıfır uzay-zaman aralığı oluşturan olaylar tarafından oluşturulan uzay ve zaman hiperboloidleri arasındaki (1+2)-boyutlu sınır, hiperboloidlerin ışık konisine dejenere edilmesiyle oluşturulur. (1+1)-boyutlarda hiperboller Şekil 2-7a'da gösterilen iki gri 45°-çizgisine dejenere olur. ⓘ
Zaman genişlemesi ve uzunluk daralması
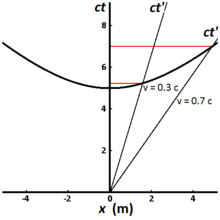
Şekil 2-8, orijinden 5 metrelik (yaklaşık 1.67×10-8 s) uygun bir sürede ulaşılabilen tüm olaylar için değişmez hiperbolü göstermektedir. Farklı dünya çizgileri farklı hızlarda hareket eden saatleri temsil etmektedir. Gözlemciye göre durağan olan bir saatin dünya çizgisi dikeydir ve gözlemci tarafından ölçülen geçen zaman uygun zamanla aynıdır. 0,3 c hızında hareket eden bir saat için gözlemci tarafından ölçülen geçen süre 5,24 metre (1,75×10-8 s) iken, 0,7 c hızında hareket eden bir saat için gözlemci tarafından ölçülen geçen süre 7,00 metredir (2,34×10-8 s). Bu, zaman genişlemesi olarak bilinen olguyu göstermektedir. Daha hızlı hareket eden saatlerin aynı miktarda uygun zamanı işaretlemesi (gözlemci çerçevesinde) daha uzun sürer ve bu uygun zaman içinde x ekseni boyunca zaman genişlemesi olmadan yapabileceklerinden daha fazla yol alırlar. Zaman genişlemesinin farklı eylemsiz referans çerçevelerindeki iki gözlemci tarafından ölçülmesi karşılıklıdır. Eğer O gözlemcisi O′ gözlemcisinin saatlerini kendi çerçevesinde daha yavaş çalışıyormuş gibi ölçerse, O′ gözlemcisi de O gözlemcisinin saatlerini daha yavaş çalışıyormuş gibi ölçecektir. ⓘ

Zaman genişlemesi gibi uzunluk daralması da eşzamanlılığın göreliliğinin bir tezahürüdür. Uzunluk ölçümü, kişinin referans çerçevesinde eşzamanlı olan iki olay arasındaki uzay-zaman aralığının ölçülmesini gerektirir. Ancak bir referans çerçevesinde eşzamanlı olan olaylar, genel olarak, diğer referans çerçevelerinde eşzamanlı değildir. ⓘ
Şekil 2-9 x ekseni boyunca 0,5 c hızla hareket eden 1 m'lik bir çubuğun hareketlerini göstermektedir. Mavi bandın kenarları çubuğun iki uç noktasının dünya çizgilerini temsil etmektedir. Değişmez hiperbol, orijinden 1 m'lik uzay benzeri bir aralıkla ayrılan olayları göstermektedir. t′ = 0 olduğunda ölçülen O ve B uç noktaları S′ çerçevesinde eşzamanlı olaylardır. Ancak S çerçevesindeki bir gözlemci için O ve B olayları eşzamanlı değildir. Uzunluğu ölçmek için, S çerçevesindeki gözlemci çubuğun uç noktalarını kendi dünya çizgileri boyunca x-eksenine yansıtılmış olarak ölçer. Çubuğun dünya tabakasının x eksenine izdüşümü, kısaltılmış OC uzunluğunu verir. ⓘ
(gösterilmemiştir) A'dan x′ eksenini kesecek şekilde dikey bir çizgi çizilmesi, OB'nin O gözlemcisinin bakış açısından kısaltılmış olmasına rağmen, OA'nın da O′ gözlemcisinin bakış açısından aynı şekilde kısaltılmış olduğunu gösterir. Her gözlemcinin diğerinin saatini yavaş çalışıyormuş gibi ölçmesi gibi, her gözlemci de diğerinin cetvelini daralmış olarak ölçer. ⓘ
Karşılıklı uzunluk daralması ile ilgili olarak, Şekil 2-9, astarlanmış ve astarsız çerçevelerin karşılıklı olarak hiperbolik bir açıyla (Öklid geometrisindeki sıradan açılara benzer şekilde) döndürüldüğünü göstermektedir. Bu dönme nedeniyle, astarlanmış bir metre çubuğunun astarsız x ekseni üzerindeki izdüşümü kısalırken, astarsız bir metre çubuğunun astarlanmış x′ ekseni üzerindeki izdüşümü de aynı şekilde kısalır. ⓘ
Karşılıklı zaman genişlemesi ve ikiz paradoksu
Karşılıklı zaman genişlemesi
Karşılıklı zaman genişlemesi ve uzunluk daralması, yeni başlayanlara doğası gereği kendi içinde çelişen kavramlar olarak görünme eğilimindedir. Eğer S çerçevesindeki bir gözlemci, S' S'de v hızıyla hareket ederken, S' çerçevesinde hareketsiz duran bir saati kendi saatinden daha yavaş çalışıyor olarak ölçerse, görelilik ilkesi S' çerçevesindeki bir gözlemcinin de aynı şekilde S'de -v hızıyla hareket eden bir saati kendi saatinden daha yavaş çalışıyor olarak ölçmesini gerektirir. İki saatin nasıl olup da her ikisinin de diğerinden daha yavaş çalışabildiği, "özel göreliliği anlamanın kalbine giden" önemli bir sorudur. ⓘ
Bu bariz çelişki, gerekli, ilgili ölçümlerin farklı ayarlarının doğru bir şekilde dikkate alınmamasından kaynaklanmaktadır. Bu ayarlar, görünürdeki tek çelişkinin tutarlı bir şekilde açıklanmasını sağlar. Mesele iki özdeş saatin soyut tik takları değil, hareketli bir saatin iki tik takının zamansal mesafesinin bir çerçevede nasıl ölçüleceğidir. Her biri ilgili çerçevede hareket eden saatlerin tik takları arasındaki sürenin karşılıklı olarak gözlemlenmesinde, farklı saat kümelerinin yer alması gerektiği ortaya çıkmaktadır. S çerçevesi içinde hareketli bir W′ saatinin (S′ içinde hareketsiz) tik süresini ölçmek için, S içinde uzamsal mesafesi d olan keyfi olarak sabit iki noktada hareketsiz iki ek, senkronize W1 ve W2 saati kullanılır.
- İki olay "iki saatin aynı anda bir yerde olması" koşuluyla tanımlanabilir, yani W′ her bir W1 ve W2'yi geçtiğinde. Her iki olay için de aynı yerde bulunan saatlerin iki okuması kaydedilir. W1 ve W2'nin iki okumasının farkı S'deki iki olayın zamansal uzaklığıdır ve uzamsal uzaklıkları d'dir. W′'nin iki okumasının farkı S′'deki iki olayın zamansal uzaklığıdır. S′'de bu olaylar sadece zaman olarak ayrılmıştır, S′'de aynı yerde gerçekleşirler. Bu iki olayın kapsadığı uzay-zaman aralığının değişmezliği ve S'deki sıfır olmayan d uzaysal ayrımı nedeniyle, S′'deki zamansal mesafe S'dekinden daha küçük olmalıdır: hareketli saat W′'nin okumalarından kaynaklanan iki olay arasındaki daha küçük zamansal mesafe, daha yavaş çalışan saat W′'ye aittir. ⓘ
Tersine, S′ çerçevesindeki hareketli bir W saatindeki (S'de hareketsiz) iki olayın zamansal mesafesini değerlendirmek için, S′'de hareketsiz iki saate ihtiyaç vardır.
- Bu karşılaştırmada W saati -v hızıyla hareket etmektedir. "Bir yerde aynı anda iki saat" ile tanımlanan olaylar için dört okumanın tekrar kaydedilmesi, şimdi S′'de zamansal ve uzamsal olarak ayrılmış ve S'de yalnızca zamansal olarak ayrılmış ancak bir arada bulunan iki olayın benzer zamansal mesafeleriyle sonuçlanır. Uzay-zaman aralığını değişmez tutmak için, S′'deki olayların uzamsal olarak ayrılması nedeniyle S'deki zamansal mesafe S′'dekinden daha küçük olmalıdır: şimdi W saatinin daha yavaş çalıştığı gözlemlenmektedir. ⓘ
Sırasıyla S veya S′'de "hareket eden bir saat" ve "hareketsiz iki saat" ile iki yargı için gerekli kayıtlar, her biri üç saat içeren iki farklı küme içerir. Ölçümlerde farklı saat kümeleri söz konusu olduğundan, ölçümlerin karşılıklı olarak "tutarlı" olması, yani bir gözlemcinin hareketli saati yavaş olarak ölçmesi halinde diğer gözlemcinin de onun saatini hızlı olarak ölçmesi gibi doğal bir gereklilik yoktur. ⓘ
Şekil 2-10, Minkowski diyagramları ile karşılıklı zaman genişlemesinin önceki tartışmasını göstermektedir. Üstteki resim, astarlanmamış, dikdörtgen eksenlerle "hareketsiz" S çerçevesinden ve astarlanmış, eğik eksenlerle koordinatlandırılmış, sağa eğimli "v > 0 ile hareket eden" S′ çerçevesinden görülen ölçümleri yansıtmaktadır; alttaki resim ise astarlanmış, dikdörtgen koordinatlarla "hareketsiz" S′ çerçevesini ve astarlanmamış, eğik eksenlerle sola eğimli "-v < 0 ile hareket eden" S çerçevesini göstermektedir. ⓘ
Bir uzamsal eksene (x, x′) paralel çizilen her çizgi bir eşzamanlılık çizgisini temsil eder. Böyle bir çizgi üzerindeki tüm olaylar aynı zaman değerine (ct, ct′) sahiptir. Aynı şekilde, zamansal bir eksene paralel çizilen her çizgi (ct, ct′) eşit uzamsal koordinat değerlerine sahip bir çizgiyi (x, x′) temsil eder. ⓘ
- Her iki resimde de O (= O′) orijini, her iki karşılaştırmada da ilgili "hareketli saatin" "hareketsiz ilk saat" ile aynı yerde bulunduğu olay olarak belirlenebilir. Açıkçası, bu olay için her iki karşılaştırmada da her iki saatin okumaları sıfırdır. Sonuç olarak, hareketli saatlerin dünya çizgileri sağa eğik ct′ ekseni (üstteki resimler, W′ saati) ve sola eğik ct eksenleridir (alttaki resimler, W saati). W1 ve W′1'in dünya çizgileri karşılık gelen dikey zaman eksenleridir (üst resimlerde ct ve alt resimlerde ct′). ⓘ
- Üstteki resimde W2'nin yeri Ax > 0 olarak alınmıştır ve dolayısıyla bu saatin dünya çizgisi (resimlerde gösterilmemiştir) A olarak etiketlenen olayda hareketli saatin dünya çizgisiyle (ct′-ekseni) kesişir, burada "iki saat aynı anda bir yerdedir". Alttaki resimde W′2 için yer Cx′ < 0 olarak alınır ve bu ölçümde hareketli saat W, C olayında W′2'yi geçer. ⓘ
- Üstteki resimde A olayının ct-koordinatı At (W2'nin okunması) B olarak etiketlenir, böylece W1 ve W2 ile ölçülen iki olay arasında geçen süre OB olarak verilir. Karşılaştırma için, W′ ile ölçülen OA zaman aralığının uzunluğu ct ekseninin ölçeğine dönüştürülmelidir. Bu, A'dan geçen ve orijinden A ile aynı uzay-zaman aralığına sahip tüm olayları birbirine bağlayan değişmez hiperbol (bkz. ayrıca Şekil 2-8) ile yapılır: OC < OB, "hareketli" saat W′ daha yavaş çalışır. ⓘ
Üstteki resimde karşılıklı zaman genişlemesini hemen göstermek için, D olayı x′ = 0'da (S′'deki W′ saatinin konumu), S′'deki C (OC, OA ile eşit uzay-zaman aralığına sahiptir) ile eşzamanlı olan olay olarak inşa edilebilir. Bu, OD zaman aralığının OA'dan daha uzun olduğunu ve "hareketli" saatin daha yavaş çalıştığını gösterir. ⓘ
Alttaki resimde S çerçevesi, hareketsiz S′ çerçevesi içinde -v hızıyla hareket etmektedir. W saatinin dünya çizgisi ct eksenidir (sola eğik), W′1'in dünya çizgisi dikey ct′ eksenidir ve W′2'nin dünya çizgisi ct′ koordinatı D olan C olayı boyunca dikeydir. C olayından geçen değişmez hiperbol, OC zaman aralığını OD'den daha kısa olan OA'ya ölçeklendirir; ayrıca B, x = 0'da S'de A ile eşzamanlı olarak inşa edilir (üst resimlerdeki D'ye benzer şekilde). OB > OC sonucu yine yukarıdakine karşılık gelir. ⓘ
"Ölçü" kelimesi önemlidir. Klasik fizikte bir gözlemci gözlemlenen bir nesneyi etkileyemez, ancak nesnenin hareket durumu gözlemcinin nesneye ilişkin gözlemlerini etkileyebilir. ⓘ
İkiz paradoksu
Özel göreliliğe giriş niteliğindeki birçok kitap, Galile göreliliği ile özel görelilik arasındaki farkları bir dizi "paradoks" ortaya koyarak açıklamaktadır. Bu paradokslar aslında, ışık hızıyla karşılaştırılabilir hızlara aşina olmamamızdan kaynaklanan, yanlış pozlanmış problemlerdir. Çözüm, özel görelilikteki birçok problemi çözmek ve onun sezgisel olmayan tahminlerine aşina olmaktır. Uzayzamanı incelemeye yönelik geometrik yaklaşım, modern bir sezgi geliştirmek için en iyi yöntemlerden biri olarak kabul edilir. ⓘ
İkiz paradoksu tek yumurta ikizlerini içeren bir düşünce deneyidir; ikizlerden biri yüksek hızlı bir roketle uzaya yolculuk yapar ve eve döndüğünde Dünya'da kalan ikizinin daha fazla yaşlanmış olduğunu görür. Bu sonuç şaşırtıcı görünmektedir çünkü ikizlerden her biri diğerini hareket ediyor olarak gözlemlemektedir ve bu nedenle ilk bakışta her birinin diğerini daha az yaşlanmış bulması gerekir. İkiz paradoksu, üçüncü bir saat gerekliliğinden kaçınarak yukarıda sunulan karşılıklı zaman genişlemesi gerekçesini ortadan kaldırmaktadır. Bununla birlikte, ikiz paradoksu gerçek bir paradoks değildir çünkü özel görelilik bağlamında kolayca anlaşılabilir. ⓘ
Bir paradoksun var olduğu izlenimi, özel göreliliğin ne ifade ettiğinin yanlış anlaşılmasından kaynaklanmaktadır. Özel görelilik tüm referans çerçevelerini eşdeğer ilan etmez, sadece eylemsiz çerçeveleri eşdeğer ilan eder. Seyahat eden ikizin çerçevesi, hızlandığı dönemlerde eylemsiz değildir. Dahası, ikizler arasındaki fark gözlemsel olarak tespit edilebilir: seyahat eden ikizin eve dönebilmek için roketlerini ateşlemesi gerekirken, evde kalan ikizin böyle bir ihtiyacı yoktur. ⓘ
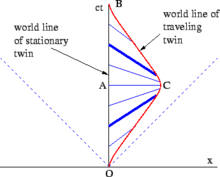
Bu farklılıklar ikizlerin yaşlarında bir farklılığa yol açmalıdır. Şekil 2-11'deki uzay-zaman diyagramı, x ekseni boyunca dümdüz giden ve hemen geri dönen bir ikizin basit durumunu göstermektedir. Evde kalan ikiz açısından bakıldığında, ikiz paradoksunda şaşırtıcı hiçbir şey yoktur. Seyahat eden ikizin dünya çizgisi boyunca O'dan C'ye ölçülen uygun zaman, artı C'den B'ye ölçülen uygun zaman, evde kalan ikizin O'dan A'ya ve B'ye ölçülen uygun zamanından daha azdır. Daha karmaşık yörüngeler, seyahat eden ikizin deneyimlediği toplam uygun zaman miktarını hesaplamak için eğri boyunca ilgili olaylar arasındaki uygun zamanı (yani yol integralini) entegre etmeyi gerektirir. ⓘ
İkiz paradoksu seyahat eden ikizin bakış açısından analiz edilirse komplikasyonlar ortaya çıkar. ⓘ
Weiss'ın evde kalan ikizi Terence ve seyahat eden ikizi Stella olarak adlandıran isimlendirmesi bundan sonra kullanılacaktır. ⓘ
Stella eylemsiz bir çerçevede değildir. Bu gerçek göz önüne alındığında, ikiz paradoksunun tam çözümünün genel görelilik gerektirdiği bazen yanlış bir şekilde ifade edilmektedir:
Saf bir SR analizi aşağıdaki gibi olacaktır: Stella'nın dinlenme çerçevesinde analiz edildiğinde, tüm yolculuk boyunca hareketsizdir. Geri dönüş için roketlerini ateşlediğinde, yerçekimi kuvvetine benzeyen sahte bir kuvvetle karşılaşır. Şekil 2-6 ve 2-11 eşzamanlılık çizgileri (düzlemleri) kavramını göstermektedir: Gözlemcinin x-eksenine paralel çizgiler (xy-düzlemi) gözlemci çerçevesinde eşzamanlı olan olay kümelerini temsil eder. Şekil 2-11'de, mavi çizgiler Terence'ın dünya çizgisi üzerindeki, Stella'nın bakış açısından, onun dünya çizgisi üzerindeki olaylarla eşzamanlı olan olayları birbirine bağlamaktadır. (Terence da bir dizi yatay eşzamanlılık çizgisi gözlemleyecektir.) Stella yolculuğunun hem gidiş hem de geliş ayakları boyunca, Terence'ın saatlerinin kendisininkinden daha yavaş çalıştığını ölçer. Ancak dönüş sırasında (yani şekildeki koyu mavi çizgiler arasında), Stella'nın eşzamanlılık çizgilerinin açısında, Terence'ın dünya çizgisinde Stella'nın kendisiyle eşzamanlı olduğunu düşündüğü olayların hızlı bir şekilde atlanmasına karşılık gelen bir kayma meydana gelir. Dolayısıyla, Stella yolculuğunun sonunda Terence'ın kendisinden daha fazla yaşlanmış olduğunu görür. ⓘ
İkiz paradoksunu analiz etmek için genel görelilik gerekli olmasa da, genel göreliliğin Eşdeğerlik İlkesi'nin uygulanması konuya ilişkin bazı ek bilgiler sağlar. Stella eylemsiz bir çerçevede durağan değildir. Stella'nın dinlenme çerçevesi içinde analiz edildiğinde, Stella tüm yolculuk boyunca hareketsizdir. Hızla ilerlerken dinlenme çerçevesi eylemsizdir ve Terence'ın saati yavaş çalışıyor gibi görünecektir. Ancak geri dönüş için roketlerini ateşlediğinde, dinlenme çerçevesi hızlandırılmış bir çerçevedir ve sanki bir yerçekimi alanındaymış gibi onu iten bir kuvvetle karşılaşır. Terence bu alanda yüksekte gibi görünecek ve yerçekimsel zaman genişlemesi nedeniyle saati hızlı çalışıyor gibi görünecektir, öyle ki net sonuç Terence'ın tekrar bir araya geldiklerinde Stella'dan daha fazla yaşlanmış olmasıdır. Yerçekimsel zaman genişlemesini öngören teorik argümanlar sadece genel göreliliğe özgü değildir. Newton'un teorisi de dahil olmak üzere, eşdeğerlik ilkesine saygı duyan herhangi bir yerçekimi teorisi yerçekimsel zaman genişlemesini öngörecektir. ⓘ
Yerçekimi
Bu giriş bölümü, tanımlanması en kolay olan özel görelilik uzayzamanına odaklanmıştır. Minkowski uzayzamanı düzdür, yerçekimini hesaba katmaz, her yerde aynıdır ve içinde gerçekleşen olaylar için statik bir arka plandan başka bir şey değildir. Yerçekiminin varlığı uzayzamanın tanımını büyük ölçüde karmaşıklaştırır. Genel görelilikte, uzay-zaman artık statik bir arka plan değildir, ancak içerdiği fiziksel sistemlerle aktif olarak etkileşime girer. Uzayzaman maddenin varlığında eğrilir, dalgaları yayabilir, ışığı bükebilir ve bir dizi başka fenomen sergiler. Bu fenomenlerden birkaçı bu makalenin ilerleyen bölümlerinde açıklanmaktadır. ⓘ
Uzayzamanın temel matematiği
Galile dönüşümleri
Temel bir amaç, göreceli hareket halindeki gözlemciler tarafından yapılan ölçümleri karşılaştırabilmektir. Bir olayın zaman ve uzay koordinatlarını ölçen S çerçevesindeki bir O gözlemcisi varsa, bu olaya üç Kartezyen koordinat ve senkronize saatler kafesinde (x, y, z, t) ölçülen zamanı atar (bkz. Şekil 1-1). Farklı bir S′ çerçevesindeki ikinci bir gözlemci O′ aynı olayı kendi koordinat sisteminde ve senkronize saatler kafesinde (x′, y′, z′, t′) ölçer. Eylemsiz çerçevelerde, gözlemcilerden hiçbiri ivme altında değildir ve basit bir denklem seti (x, y, z, t) koordinatlarını (x′, y′, z′, t′) ile ilişkilendirmemizi sağlar. İki koordinat sisteminin standart konfigürasyonda olduğu, yani paralel (x, y, z) koordinatlarıyla hizalandıkları ve t′ = 0 olduğunda t = 0 olduğu göz önüne alındığında, koordinat dönüşümü aşağıdaki gibidir:

Şekil 3-1, Newton'un teorisinde ışığın hızının değil, zamanın evrensel olduğunu göstermektedir. Aşağıdaki düşünce deneyini düşünün: Kırmızı ok, platforma göre 0,4 c hızla hareket eden bir treni göstermektedir. Tren içinde bir yolcu, trenin çerçevesi içinde 0,4 c hızında bir mermi atıyor. Mavi ok, tren rayları üzerinde duran bir kişinin merminin 0,8 c hızla hareket ettiğini ölçtüğünü göstermektedir. ⓘ
Daha genel olarak, S′ çerçevesinin S çerçevesine göre v hızıyla hareket ettiğini varsayarsak, S′ çerçevesi içinde O′ gözlemcisi u′ hızıyla hareket eden bir nesneyi ölçer. S çerçevesine göre u hızı, x = ut, x′ = x - vt ve t = t′ olduğundan, x′ = ut - vt = (u - v)t = (u - v)t′ şeklinde yazılabilir. Bu da u′ = x′/t′ ve sonuç olarak
- veya ⓘ
Bu da hızların toplanması için sağduyulu Galile yasasıdır. ⓘ
Hızların rölativistik bileşimi

Rölativistik uzayzamanda hızların bileşimi oldukça farklıdır. Denklemlerin karmaşıklığını biraz azaltmak için, bir nesnenin ışığa göre hızının oranı için ortak bir kısaltma getiriyoruz, ⓘ
Şekil 3-2a'da v/c = β = s/a ile verilen hızda ilerleyen kırmızı bir tren gösterilmektedir. Trenin hazır çerçevesinden bir yolcu u′/c = β′ = n/m ile verilen hızda bir mermi atıyor, burada mesafe siyah x eksenine paralel değil kırmızı x′ eksenine paralel bir çizgi boyunca ölçülüyor. Mavi okla gösterildiği gibi merminin platforma göre bileşik hızı u nedir? Şekil 3-2b'ye bakınız:
- Platformdan bakıldığında, merminin bileşik hızı u = c(s + r)/(a + b) ile verilir.
- İki sarı üçgen benzerdir çünkü ortak bir α açısını paylaşan dik üçgenlerdir. Büyük sarı üçgende s/a = v/c = β oranı vardır.
- İki sarı üçgenin karşılık gelen kenarlarının oranları sabittir, böylece r/a = b/s = n/m = β′ olur. Yani b = u′s/c ve r = u′a/c.
- Einstein'ın hızların toplanması formülünü elde etmek için b ve r ifadelerini 1. adımdaki u ifadesinde yerine koyun:
Yukarıda sunulan hızların toplanması için rölativistik formül birkaç önemli özellik sergiler:
- Eğer u′ ve v ışık hızına kıyasla çok küçükse, o zaman vu′/c2 çarpımı yok denecek kadar küçük olur ve genel sonuç hızların toplanması için Galile formülünden (Newton'un formülü) ayırt edilemez hale gelir: u = u′ + v. Galile formülü, düşük hızlar için geçerli olan rölativistik formülün özel bir durumudur.
- Eğer u′ c'ye eşitlenirse, v'nin başlangıç değeri ne olursa olsun formül u = c sonucunu verir. Işığın hızı, yayıcı kaynağa göre hareketleri ne olursa olsun tüm gözlemciler için aynıdır. ⓘ
Zaman genişlemesi ve uzunluk daralması tekrar gözden geçirildi

Zaman genişlemesi ve uzunluk daralması için nicel ifadeler elde etmek kolaydır. Şekil 3-3, bu bölümün amaçları doğrultusunda basitleştirilmiş ve yeniden etiketlenmiş, önceki iki animasyondan alınan ayrı kareleri içeren birleşik bir görüntüdür. ⓘ
Denklemlerin karmaşıklığını biraz azaltmak için, ct için çeşitli farklı kısaltma gösterimleri vardır:
- ve yaygındır.
- Ayrıca şu konvansiyonun kullanımına da çok sık rastlanmaktadır ⓘ

Şekil 3-3a'da OA ve OK segmentleri eşit uzay-zaman aralıklarını temsil etmektedir. Zaman genişlemesi OB/OK oranı ile temsil edilmektedir. Değişmez hiperbol w = √x2 + k2 denklemine sahiptir, burada k = OK'dir ve hareket halindeki bir parçacığın dünya çizgisini temsil eden kırmızı çizgi w = x/β = xc/v denklemine sahiptir. Biraz cebirsel manipülasyon sonucunda ⓘ
Karekök sembolünü içeren ifade görelilikte çok sık görülür ve ifadenin bir üstü Lorentz faktörü olarak adlandırılır ve Yunan harfi gama ile gösterilir :
Eğer v, c'ye eşit veya büyükse, aşağıdaki ifade kullanılır fiziksel olarak anlamsız hale gelir ve c'nin doğada mümkün olan maksimum hız olduğunu ima eder. Sıfırdan büyük herhangi bir v için Lorentz faktörü birden büyük olacaktır, ancak eğrinin şekli düşük hızlar için Lorentz faktörünün bire son derece yakın olmasını sağlayacak şekildedir. ⓘ
Şekil 3-3b'de OA ve OK segmentleri eşit uzay-zaman aralıklarını temsil etmektedir. Uzunluk daralması OB/OK oranı ile temsil edilir. Değişmez hiperbol x = √w2 + k2 denklemine sahiptir, burada k = OK'dir ve hareket halindeki bir çubuğun uç noktalarının dünya çizgilerini temsil eden mavi bandın kenarları 1/β = c/v eğimine sahiptir. Olay A'nın koordinatları (x, w) = (γk, γβk). A ve B'den geçen teğet doğrusu w = (x - OB)/β denklemine sahip olduğundan, γβk = (γk - OB)/β ve
Lorentz dönüşümleri
Galile dönüşümleri ve bunun sonucu olarak ortaya çıkan hızların toplanmasıyla ilgili sağduyulu yasa, uçaklar, arabalar ve toplardan oluşan düşük hızlı sıradan dünyamızda iyi işlemektedir. Ancak 1800'lü yılların ortalarından itibaren hassas bilimsel araçlar, hızların olağan toplanmasına uymayan anomaliler bulmaya başladı. ⓘ
Lorentz dönüşümleri, özel görelilikte bir olayın koordinatlarını bir çerçeveden diğerine dönüştürmek için kullanılır. ⓘ
Lorentz faktörü Lorentz dönüşümlerinde ortaya çıkar:
Ters Lorentz dönüşümleri şunlardır:
v ≪ c ve x yeterince küçük olduğunda, v2/c2 ve vx/c2 terimleri sıfıra yaklaşır ve Lorentz dönüşümleri Galile dönüşümlerine yaklaşır. ⓘ
vb. çoğu zaman gerçekten şu anlama gelir vb. Her ne kadar Lorentz dönüşümü denklemleri kısalık için deltalar olmadan yazılsa da, x Δx, vb. anlamına gelir. Genel olarak, her zaman olaylar arasındaki uzay ve zaman farklarıyla ilgileniriz. ⓘ
Dönüşümlerin bir setini normal Lorentz dönüşümleri, diğerini ise ters dönüşümler olarak adlandırmak yanıltıcıdır, çünkü çerçeveler arasında içsel bir fark yoktur. Farklı yazarlar dönüşümlerden birini ya da diğerini "ters" küme olarak adlandırmaktadır. S çerçevesi S′'ye göre yalnızca ileri ya da geri hareket edebileceğinden, ileri ve ters dönüşümler birbirleriyle önemsiz bir şekilde ilişkilidir. Dolayısıyla denklemleri tersine çevirmek, basitçe öncelenmiş ve öncelenmemiş değişkenleri değiştirmeyi ve v'yi -v ile değiştirmeyi gerektirir. ⓘ
Örnek: Terence ve Stella Dünya'dan Mars'a yapılan bir uzay yarışında. Terence başlangıç çizgisinde bir görevli, Stella ise bir katılımcıdır. t = t′ = 0 zamanında, Stella'nın uzay gemisi anlık olarak 0,5 c hızına çıkar. Dünya'dan Mars'a olan mesafe 300 ışık saniyesidir (yaklaşık 90,0×106 km). Terence Stella'nın bitiş çizgisini t = 600.00 s'de geçtiğini gözlemler. Ancak Stella gemi kronometresindeki zamanı Bitiş çizgisini geçerken, başlangıç ve bitiş çizgileri arasındaki mesafeyi kendi çerçevesinden ölçerek 259,81 ışık saniyesi (yaklaşık 77,9×106 km) olarak hesaplar. 1). ⓘ
Lorentz dönüşümlerinin türetilmesi

Einstein'ın 1905'teki orijinal çalışmasından bu yana Lorentz dönüşümlerinin, her biri kendine özgü bir odağa sahip düzinelerce türevi yapılmıştır. Einstein'ın türetmesi ışık hızının değişmezliğine dayansa da, başlangıç noktası olarak kullanılabilecek başka fiziksel ilkeler de vardır. Nihayetinde bu alternatif başlangıç noktaları, bir parçacığın diğerine uyguladığı etkinin anlık olarak aktarılamayacağını ifade eden temel yerellik ilkesinin farklı ifadeleri olarak düşünülebilir. ⓘ
Burada verilen ve Şekil 3-5'te gösterilen türetme Bais tarafından sunulana dayanmaktadır ve Hızların Göreli Bileşimi, Zaman Genişlemesi ve Uzunluk Daralması bölümlerindeki önceki sonuçlardan yararlanmaktadır. P olayı siyah "dinlenme sisteminde" (w, x) koordinatlarına ve β = v/c hız parametresiyle hareket eden kırmızı çerçevede (w′, x′) koordinatlarına sahiptir. w′ ve x′ koordinatlarını w ve x cinsinden (ya da tam tersi şekilde) belirlemek için öncelikle ters Lorentz dönüşümünü türetmek daha kolaydır.
- Enine yönlerde uzunluk genişlemesi/büzülmesi diye bir şey olamaz. y' y'ye ve z′ z'ye eşit olmalıdır, aksi takdirde hızlı hareket eden 1 m'lik bir topun 1 m'lik dairesel bir delikten geçip geçemeyeceği gözlemciye bağlı olacaktır. Göreliliğin ilk önermesi tüm eylemsiz çerçevelerin eşdeğer olduğunu belirtir ve enine genişleme/büzülme bu yasayı ihlal eder.
- Çizimden, w = a + b ve x = r + s
- Benzer üçgenleri kullanan önceki sonuçlardan, s/a = b/r = v/c = β olduğunu biliyoruz.
- Zaman genişlemesi nedeniyle, a = γw′
- Denklem (4)'ü s/a = β denkleminde yerine koyduğumuzda s = γw′β elde edilir.
- Uzunluk daralması ve benzer üçgenler bize r = γx′ ve b = βr = βγx′ verir.
- Adım 2'deki denklemlerde s, a, r ve b ifadelerinin yerine konulmasıyla aşağıdaki sonuçlar elde edilir
Yukarıdaki denklemler, w yerine ct, w′ yerine ct′ ve β yerine v/c konularak görülebileceği gibi, ters Lorentz dönüşümünün t ve x denklemleri için alternatif ifadelerdir. Ters dönüşümden, ileri dönüşümün denklemleri t′ ve x′ için çözülerek türetilebilir. ⓘ
Lorentz dönüşümlerinin doğrusallığı
Lorentz dönüşümleri doğrusallık adı verilen matematiksel bir özelliğe sahiptir, çünkü x′ ve t′ x ve t'nin doğrusal kombinasyonları olarak elde edilir, daha yüksek güçler dahil değildir. Dönüşümün doğrusallığı, türetmede zımnen varsayılan uzayzamanın temel bir özelliğini, yani eylemsiz referans çerçevelerinin özelliklerinin konum ve zamandan bağımsız olduğunu yansıtır. Yerçekimi olmadığında, uzayzaman her yerde aynı görünür. Tüm eylemsiz gözlemciler ivmelenen ve ivmelenmeyen hareketi neyin oluşturduğu konusunda hemfikir olacaktır. Herhangi bir gözlemci kendi uzay ve zaman ölçümlerini kullanabilir, ancak bunlar hakkında mutlak bir şey yoktur. Başka bir gözlemcinin konvansiyonları da aynı işi görecektir. ⓘ
Doğrusallığın bir sonucu, iki Lorentz dönüşümü ardışık olarak uygulanırsa, sonucun da bir Lorentz dönüşümü olmasıdır. ⓘ
Örnek: Terence, Stella'nın kendisinden 0,500 c hızla uzaklaştığını gözlemler ve Stella'nın ölçümlerini kendi ölçümleriyle ilişkilendirmek için Lorentz dönüşümlerini β = 0,500 ile kullanabilir. Stella, kendi çerçevesinde, Ursula'nın kendisinden 0.250 c hızla uzaklaştığını gözlemler ve Ursula'nın ölçümlerini kendi ölçümleriyle ilişkilendirmek için β = 0.250 ile Lorentz dönüşümlerini kullanabilir. Dönüşümlerin doğrusallığı ve hızların rölativistik bileşimi nedeniyle Terence, Ursula'nın ölçümlerini kendi ölçümleriyle ilişkilendirmek için Lorentz dönüşümlerini β = 0,666 ile kullanabilir. ⓘ
Doppler etkisi
Doppler etkisi, göreceli hareket halindeki bir alıcı ve kaynak için bir dalganın frekans veya dalga boyundaki değişimdir. Basitlik açısından, burada iki temel senaryoyu ele alıyoruz: (1) Kaynak ve/veya alıcının hareketleri tam olarak onları birleştiren doğru boyunca (boylamsal Doppler etkisi) ve (2) hareketler söz konusu doğruya dik açılardadır (enine Doppler etkisi). Ara açılar boyunca hareket ettikleri senaryoları göz ardı ediyoruz. ⓘ
Boylamsal Doppler etkisi
Klasik Doppler analizi, ses dalgaları veya su dalgaları gibi bir ortamda yayılan ve birbirlerine doğru veya birbirlerinden uzaklaşan kaynaklar ve alıcılar arasında iletilen dalgalarla ilgilenir. Bu tür dalgaların analizi, kaynağın, alıcının veya her ikisinin de ortama göre hareket edip etmediğine bağlıdır. Alıcının ortama göre sabit olduğu ve kaynağın βs hız parametresi için vs hızıyla alıcıdan doğrudan uzaklaştığı senaryo göz önüne alındığında, dalga boyu artar ve gözlemlenen frekans f şu şekilde verilir
Öte yandan, kaynağın sabit olduğu ve alıcının βr hız parametresi için vr hızıyla kaynaktan doğrudan uzaklaştığı senaryo göz önüne alındığında, dalga boyu değişmez, ancak dalgaların alıcıya göre iletim hızı azalır ve gözlenen frekans f şu şekilde verilir
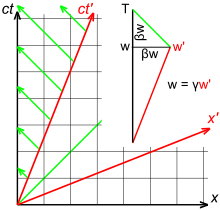
Işık, ses veya su dalgalarının aksine, bir ortam içinde yayılmaz ve alıcıdan uzaklaşan bir kaynak veya kaynaktan uzaklaşan bir alıcı arasında bir ayrım yoktur. Şekil 3-6, alıcıdan β hız parametresiyle ayrılan bir kaynağı gösteren rölativistik bir uzay-zaman diyagramını göstermektedir, böylece w zamanında kaynak ve alıcı arasındaki ayrım βw olur. Zaman genişlemesi nedeniyle, . Yeşil ışık ışınının eğimi -1 olduğu için, . Dolayısıyla, göreli Doppler etkisi şu şekilde verilir
Enine Doppler etkisi

Kesişmeyen doğrular boyunca düzgün eylemsiz hareketle birbirlerine yaklaşan bir kaynak ve bir alıcının birbirlerine en yakın mesafede olduklarını varsayalım. Klasik analizin, alıcının hiçbir Doppler kayması algılamayacağını öngördüğü görülecektir. Analizdeki incelikler nedeniyle, bu beklenti her zaman doğru olmayabilir. Bununla birlikte, uygun şekilde tanımlandığında, enine Doppler kayması klasik bir benzeri olmayan göreli bir etkidir. İncelikler şunlardır:
- Şekil 3-7a. Alıcı kaynağa geometrik olarak en yakın konumdayken frekans ölçümü nedir? Bu senaryo en kolay şekilde kaynağın S' çerçevesinden analiz edilebilir.
- Şekil 3-7b. Alıcı kaynağı kendisine en yakın olarak gördüğünde frekans ölçümü nedir? Bu senaryo en kolay alıcının S çerçevesinden analiz edilebilir.
Diğer iki senaryo genellikle enine Doppler kayması tartışmalarında incelenir:
- Şekil 3-7c. Alıcı kaynağın etrafında bir daire çizerek hareket ediyorsa, alıcı hangi frekansı ölçer?
- Şekil 3-7d. Kaynak alıcının etrafında bir daire çizerek hareket ediyorsa, alıcı hangi frekansı ölçer?
Senaryo (a)'da, en yakın yaklaşma noktası çerçeveden bağımsızdır ve zamana karşı mesafede herhangi bir değişimin olmadığı (yani dr/dt = 0, burada r alıcı ile kaynak arasındaki mesafedir) ve dolayısıyla boylamsal Doppler kaymasının olmadığı anı temsil eder. Kaynak, alıcıyı f′ frekanslı ışıkla aydınlatılmış olarak gözlemler, ancak aynı zamanda alıcıyı zamanı kısaltılmış bir saate sahip olarak gözlemler. Dolayısıyla S karesinde alıcı, frekansı f′ olan maviye kaymış ışık tarafından aydınlatılmaktadır.
Senaryo (b)'de, kaynak hareket etmiş olmasına rağmen, alıcının kaynağın alıcıya en yakın olduğu andaki ışıkla aydınlatıldığı gösterilmektedir. Kaynağın saatleri S çerçevesinden ölçüldüğünde zaman genişlemesine uğradığından ve dr/dt bu noktada sıfıra eşit olduğundan, kaynaktan gelen ve bu en yakın noktadan yayılan ışık frekansla kırmızıya kayar
Senaryolar (c) ve (d) basit zaman genişlemesi argümanlarıyla analiz edilebilir. (c)'de alıcı, kaynaktan gelen ışığın şu kadarlık bir faktörle maviye kaydığını gözlemler ve (d)'de ışık kırmızıya kayar. Görünürdeki tek komplikasyon yörüngede dönen nesnelerin ivmeli hareket halinde olmasıdır. Ancak, eylemsiz bir gözlemci hızlanan bir saate bakıyorsa, zaman genişlemesi hesaplanırken yalnızca saatin anlık hızı önemlidir. (Ancak tersi doğru değildir.) Enine Doppler kayması raporlarının çoğu etkiyi kırmızıya kayma olarak adlandırır ve etkiyi (b) veya (d) senaryoları açısından analiz eder. ⓘ
Enerji ve momentum
Momentumun dört boyuta genişletilmesi

Klasik mekanikte, bir parçacığın hareket durumu kütlesi ve hızı ile karakterize edilir. Bir parçacığın kütlesi ve hızının çarpımı olan doğrusal momentum, hız ile aynı yöne sahip olan vektörel bir niceliktir: p = mv. Korunan bir niceliktir, yani kapalı bir sistem dış kuvvetlerden etkilenmiyorsa, toplam doğrusal momentumu değişmez. ⓘ
Rölativistik mekanikte momentum vektörü dört boyuta genişletilir. Momentum vektörüne, uzay-zaman momentum vektörünün uzay-zaman konum vektörü gibi dönüşmesini sağlayan bir zaman bileşeni eklenir . Uzay-zaman momentumunun özelliklerini incelerken, Şekil 3-8a'da bir parçacığın durgun halde nasıl göründüğünü inceleyerek başlıyoruz. Durağan çerçevede, momentumun uzaysal bileşeni sıfırdır, yani p = 0, ancak zaman bileşeni mc'ye eşittir. ⓘ
Bu vektörün hareketli çerçevedeki dönüştürülmüş bileşenlerini Lorentz dönüşümlerini kullanarak elde edebiliriz ya da doğrudan şekilden okuyabiliriz çünkü biliyoruz ki ve Çünkü kırmızı eksenler gama ile yeniden ölçeklendirilmiştir. Şekil 3-8b durumu hareketli çerçevede göründüğü şekliyle göstermektedir. Hareketli çerçevenin hızı c'ye yaklaştıkça dört-momentumun uzay ve zaman bileşenlerinin sonsuza gittiği açıktır. ⓘ
Bu bilgiyi kısa bir süre sonra dört-momentum için bir ifade elde etmek için kullanacağız. ⓘ
Işık momentumu

Işık parçacıkları ya da fotonlar, geleneksel olarak ışık hızı olarak bilinen c sabit hızında hareket ederler. Bu ifade bir totoloji değildir, çünkü göreliliğin birçok modern formülasyonu bir varsayım olarak sabit ışık hızıyla başlamaz. Dolayısıyla fotonlar ışık benzeri bir dünya çizgisi boyunca yayılır ve uygun birimlerde her gözlemci için eşit uzay ve zaman bileşenlerine sahiptir. ⓘ
Maxwell'in elektromanyetizma teorisinin bir sonucu da ışığın enerji ve momentum taşıdığı ve bunların oranının bir sabit olduğudur: . Yeniden düzenlersek, Fotonlar için uzay ve zaman bileşenleri eşit olduğundan, E/c bu nedenle uzay-zaman momentum vektörünün zaman bileşeni ile eşitlenmelidir. ⓘ
Fotonlar ışık hızında hareket ederler, ancak sonlu momentum ve enerjiye sahiptirler. Bunun böyle olabilmesi için γmc'deki kütle teriminin sıfır olması gerekir, yani fotonlar kütlesiz parçacıklardır. Sonsuzluk çarpı sıfır kötü tanımlanmış bir niceliktir, ancak E/c iyi tanımlanmıştır. ⓘ
Bu analize göre, eğer bir fotonun enerjisi durağan çerçevede E'ye eşitse hareket eden bir çerçevede. Bu sonuç Şekil 3-9'un incelenmesiyle veya Lorentz dönüşümlerinin uygulanmasıyla elde edilebilir ve daha önce verilen Doppler etkisi analiziyle tutarlıdır. ⓘ
Kütle-enerji ilişkisi
Rölativistik momentum vektörünün çeşitli bileşenleri arasındaki karşılıklı ilişkilerin dikkate alınması Einstein'ı birkaç ünlü sonuca götürmüştür. ⓘ
- Düşük hız sınırında β = v/c sıfıra yaklaştıkça, γ 1'e yaklaşır, dolayısıyla göreli momentumun uzaysal bileşeni momentum için klasik terim olan mv'ye yaklaşır. Bu bakış açısını takiben, γm, m'nin göreli bir genellemesi olarak yorumlanabilir. Einstein, bir nesnenin göreli kütlesinin aşağıdaki formüle göre hız ile arttığını öne sürmüştür .
- Aynı şekilde, rölativistik momentumun zaman bileşenini fotonunkiyle karşılaştırmak, Böylece Einstein şu ilişkiye ulaşmıştır . Sıfır hız durumunda basitleştirildiğinde, bu Einstein'ın enerji ve kütleyi ilişkilendiren ünlü denklemidir. ⓘ
Kütle ve enerji arasındaki ilişkiye bakmanın bir başka yolu da düşük hızda γmc2 'nin seri açılımını düşünmektir:
İkinci terim parçacığın kinetik enerjisi için bir ifadedir. Kütle gerçekten de enerjinin başka bir biçimi gibi görünmektedir. ⓘ
Einstein'ın 1905'te ortaya attığı göreli kütle kavramı, mrel, dünyanın dört bir yanındaki parçacık hızlandırıcılarında (ya da elektron mikroskopları, eski moda renkli televizyon setleri gibi kullanımı yüksek hızlı parçacıklara bağlı olan herhangi bir enstrümanda) her gün fazlasıyla doğrulanmasına rağmen, diğer teorik gelişmelere temel teşkil eden bir kavram olmaması anlamında fizikte verimli bir kavram olduğunu kanıtlayamamıştır. Örneğin göreli kütle, genel görelilikte hiçbir rol oynamaz. ⓘ
Bu nedenle ve pedagojik kaygılarla, çoğu fizikçi şu anda kütle ve enerji arasındaki ilişkiye atıfta bulunurken farklı bir terminolojiyi tercih etmektedir. "Rölativistik kütle" artık kullanılmayan bir terimdir. "Kütle" terimi kendi başına durgun kütleyi veya değişmez kütleyi ifade eder ve göreli momentum vektörünün değişmez uzunluğuna eşittir. Formül olarak ifade edilir,
Bu formül hem kütlesiz hem de kütleli tüm parçacıklar için geçerlidir. Mrest'in sıfıra eşit olduğu fotonlar için, . ⓘ
Dört momentum
Kütle ve enerji arasındaki yakın ilişki nedeniyle, dört-momentum (4-momentum olarak da adlandırılır) enerji-momentum 4-vektörü olarak da adlandırılır. Dört-momentumu temsil etmek için büyük harf P ve uzaysal momentumu göstermek için küçük harf p kullanarak, dört-momentum şu şekilde yazılabilir
- ya da alternatif olarak,
- kuralını kullanarak ⓘ
Koruma yasaları
Fizikte korunum yasaları, yalıtılmış bir fiziksel sistemin belirli ölçülebilir özelliklerinin, sistem zaman içinde geliştikçe değişmediğini belirtir. 1915 yılında Emmy Noether, her bir korunum yasasının altında doğanın temel bir simetrisinin yattığını keşfetti. Fiziksel süreçlerin uzayın neresinde gerçekleştiğinin önemli olmaması (uzay öteleme simetrisi) momentumun korunumunu, bu tür süreçlerin ne zaman gerçekleştiğinin önemli olmaması (zaman öteleme simetrisi) enerjinin korunumunu vb. ortaya çıkarır. Bu bölümde, kütle, momentum ve enerjinin korunumuna ilişkin Newtoncu görüşleri göreceli bir bakış açısıyla inceleyeceğiz. ⓘ
Toplam momentum
Newtoncu momentumun korunumu görüşünün göreceli bir bağlamda nasıl değiştirilmesi gerektiğini anlamak için, tek bir boyutla sınırlı iki çarpışan cisim problemini inceleyeceğiz. ⓘ
Newton mekaniğinde, bu problemin minimum karmaşıklıkta matematik sağlayan iki uç durumu ayırt edilebilir:
- (1) İki cisim tamamen elastik bir çarpışmada birbirlerinden geri teperler.
- (2) İki cisim birbirine yapışır ve tek bir parçacık olarak hareket etmeye devam eder. Bu ikinci durum tamamen elastik olmayan çarpışma durumudur.
Hem (1) hem de (2) durumları için momentum, kütle ve toplam enerji korunur. Ancak, elastik olmayan çarpışma durumlarında kinetik enerji korunmaz. Başlangıçtaki kinetik enerjinin belirli bir kısmı ısıya dönüşür. ⓘ
(2) numaralı durumda, momentumları aynı olan iki kütle ve kütlesi korunmuş tek bir parçacık üretmek için çarpışırlar orijinal sistemin kütle merkezi hızında hareket eder, . Toplam momentum korunur. ⓘ
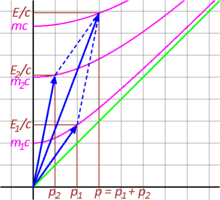
Şekil 3-10 iki parçacığın elastik olmayan çarpışmasını rölativistik bir perspektiften göstermektedir. Zaman bileşenleri ve toplamı, sonuç vektörünün toplam E/c'sine eşittir, bu da enerjinin korunduğu anlamına gelir. Aynı şekilde, uzay bileşenleri ve sonuç vektörünün p'sini oluşturmak için toplanır. Dört-momentum, beklendiği gibi, korunmuş bir niceliktir. Ancak, toplam momentumun değişmez hiperbolünün enerji eksenini kestiği nokta tarafından verilen kaynaşmış parçacığın değişmez kütlesi, çarpışan parçacıkların değişmez kütlelerinin toplamına eşit değildir. Aslında, tek tek kütlelerin toplamından daha büyüktür: . ⓘ
Bu senaryodaki olaylara ters sırayla baktığımızda, kütlenin korunmamasının yaygın bir durum olduğunu görürüz: kararsız bir temel parçacık kendiliğinden daha hafif iki parçacığa bozunduğunda, toplam enerji korunur, ancak kütle korunmaz. Kütlenin bir kısmı kinetik enerjiye dönüşür. ⓘ
Referans çerçevelerinin seçimi
Bir analizi gerçekleĢtirmek için herhangi bir çerçeveyi seçme özgürlüğü, özellikle uygun olabilecek bir çerçeveyi seçmemize olanak tanır. Momentum ve enerji problemlerinin analizi için en uygun çerçeve genellikle "momentum merkezi çerçevesi "dir (sıfır-momentum çerçevesi veya COM çerçevesi olarak da adlandırılır). Bu, sistemin toplam momentumunun uzay bileşeninin sıfır olduğu çerçevedir. Şekil 3-11'de yüksek hızlı bir parçacığın iki yavru parçacığa ayrılması gösterilmektedir. Laboratuvar çerçevesinde, yavru parçacıklar tercihen orijinal parçacığın yörüngesi boyunca yönlendirilmiş bir yönde yayılır. Ancak COM çerçevesinde, kütleleri ve hızlarının büyüklüğü genellikle aynı olmamasına rağmen, iki yavru parçacık zıt yönlerde yayılır. ⓘ
Enerji ve momentum korunumu
Etkileşen parçacıkların Newtoncu analizinde, çerçeveler arasındaki dönüşüm basittir çünkü gerekli olan tek şey Galile dönüşümünü tüm hızlara uygulamaktır. Çünkü , momentum . Etkileşim halindeki bir parçacık sisteminin toplam momentumunun bir çerçevede korunduğu gözlemlenirse, diğer herhangi bir çerçevede de aynı şekilde korunduğu gözlemlenecektir. ⓘ
COM çerçevesinde momentumun korunumu, çarpışmadan önce ve sonra p = 0 olması gerekliliğine karşılık gelir. Newton analizinde, kütlenin korunumu şunu dikte eder . Ele aldığımız basitleştirilmiş, tek boyutlu senaryolarda, parçacıkların giden momentumlarının belirlenebilmesi için yalnızca bir ek kısıtlama gereklidir - bir enerji koşulu. Kinetik enerji kaybının olmadığı tamamen elastik bir çarpışmanın tek boyutlu durumunda, COM çerçevesindeki geri tepen parçacıkların giden hızları, gelen hızlarına tam olarak eşit ve zıt olacaktır. Kinetik enerjinin tamamen kaybolduğu tamamen elastik olmayan bir çarpışma durumunda, geri tepen parçacıkların giden hızları sıfır olacaktır. ⓘ
Newton momentumları, şu şekilde hesaplanır Lorentzian dönüşümü altında düzgün davranamaz. Hızların doğrusal dönüşümü yüksek derecede doğrusal olmayan Böylece bir çerçevede momentumun korunumunu gösteren bir hesaplama diğer çerçevelerde geçersiz olacaktır. Einstein ya momentumun korunumundan vazgeçmek ya da momentumun tanımını değiştirmekle karşı karşıyaydı. Bu ikinci seçeneği tercih etti. ⓘ
Enerji ve momentum için rölativistik korunum yasası, enerji, momentum ve kütle için üç klasik korunum yasasının yerini alır. Kütle artık bağımsız olarak korunmaz, çünkü toplam rölativistik enerjiye dahil edilmiştir. Bu, enerjinin göreli korunumunu göreli olmayan mekaniğe göre daha basit bir kavram haline getirir, çünkü toplam enerji herhangi bir niteleme olmaksızın korunur. Isıya ya da iç potansiyel enerjiye dönüşen kinetik enerji kütlede bir artış olarak ortaya çıkar. ⓘ
Örnek: Kütle ve enerjinin eşdeğerliği nedeniyle, temel parçacık kütleleri geleneksel olarak enerji birimlerinde belirtilir; burada 1 MeV = 106 elektron volttur. Yüklü bir pion, 139,57 MeV kütleli bir parçacıktır (elektron kütlesinin yaklaşık 273 katı). Kararsızdır ve 105,66 MeV kütleli bir müona (elektron kütlesinin yaklaşık 207 katı) ve neredeyse ihmal edilebilir bir kütleye sahip olan bir antinötrinoya bozunur. Pion kütlesi ile müon kütlesi arasındaki fark 33,91 MeV'dir.
π−
→
μ−
+
ν
μ ⓘ
Şekil 3-12a, pionun dinlenme çerçevesinde bu bozunma reaksiyonu için enerji-momentum diyagramını göstermektedir. İhmal edilebilir kütlesi nedeniyle, bir nötrino neredeyse ışık hızında hareket eder. Enerjisinin göreli ifadesi, fotonunki gibi, şöyledir Bu aynı zamanda momentumunun uzay bileşeninin değeridir. Momentumu korumak için, müon nötrinonun momentumunun uzay bileşeninin aynı değerine sahiptir, ancak ters yöndedir. ⓘ
Bu bozunma reaksiyonunun enerjetiğinin cebirsel analizleri internette mevcuttur, bu nedenle Şekil 3-12b bunun yerine bir grafik hesap makinesi çözümü sunmaktadır. Nötrinonun enerjisi 29,79 MeV ve müonun enerjisi 33,91 MeV - 29,79 MeV = 4,12 MeV'dir. Enerjinin çoğu sıfıra yakın kütleli nötrino tarafından taşınır. ⓘ
Temellerin ötesinde
Bu bölümdeki konular önceki bölümlerdekilere kıyasla önemli ölçüde daha fazla teknik zorluk içermektedir ve eğri uzay-zamana girişin anlaşılması için gerekli değildir. ⓘ
Hızlılık

Lorentz dönüşümleri, bir referans çerçevesindeki olayların koordinatlarını başka bir çerçeveninkilerle ilişkilendirir. Hızların göreli bileşimi iki hızı birbirine eklemek için kullanılır. İkinci hesaplamaları gerçekleştiren formüller doğrusal değildir, bu da onları karşılık gelen Galile formüllerinden daha karmaşık hale getirir. ⓘ
Bu doğrusal olmayan durum, parametre seçimimizin bir eseridir. Daha önce bir x-ct uzay-zaman diyagramında, orijinden itibaren bazı sabit uzay-zaman aralıklarındaki noktaların değişmez bir hiperbol oluşturduğunu belirtmiştik. Ayrıca, standart konfigürasyondaki iki uzay-zaman referans çerçevesinin koordinat sistemlerinin birbirlerine göre hiperbolik olarak döndürüldüğünü de belirtmiştik. ⓘ
Bu ilişkileri ifade etmek için doğal fonksiyonlar trigonometrik fonksiyonların hiperbolik analoglarıdır. Şekil 4-1a sin(a) ve cos(a) ile bir birim çemberi göstermektedir; bu diyagram ile temel trigonometrinin tanıdık birim çemberi arasındaki tek fark, a'nın ışın ile x ekseni arasındaki açı olarak değil, x ekseninden ışın tarafından süpürülen sektörün alanının iki katı olarak yorumlanmasıdır. (Sayısal olarak, birim çember için açı ve 2 × alan ölçüleri aynıdır). Şekil 4-1b sinh(a) ve cosh(a) ile bir birim hiperbolü göstermektedir, burada a aynı şekilde renkli alanın iki katı olarak yorumlanır. Şekil 4-2 sinh, cosh ve tanh fonksiyonlarının çizimlerini sunmaktadır. ⓘ
Birim daire için, ışının eğimi şu şekilde verilir ⓘ
Kartezyen düzlemde, (x, y) noktasının (x', y') noktasına θ açısı ile dönüşü şu şekilde verilir
Bir uzayzaman diyagramında, hız parametresi eğimin analogudur. Hız, φ, şu şekilde tanımlanır ⓘ
burada ⓘ
Yukarıda tanımlanan hızlılık özel görelilikte çok kullanışlıdır çünkü birçok ifade onun cinsinden ifade edildiğinde çok daha basit bir biçim alır. Örneğin, hızlılık basitçe kollineer hız-ekleme formülünde toplanabilir; ⓘ
ya da başka bir deyişle, ⓘ
Lorentz dönüşümleri hız cinsinden ifade edildiğinde basit bir biçim alır. γ faktörü şu şekilde yazılabilir ⓘ
Uzay koordinat eksenlerinde dönme olmaksızın tekdüze hız ile göreli hareketi tanımlayan dönüşümler boost olarak adlandırılır. ⓘ
γ ve γβ dönüşümleri daha önce sunulduğu gibi matris formunda yeniden yazıldığında, x yönündeki Lorentz artışı şu şekilde yazılabilir
ve x yönündeki ters Lorentz artışı şu şekilde yazılabilir
Başka bir deyişle, Lorentz artışları Minkowski uzayzamanında hiperbolik dönüşleri temsil eder. ⓘ
Hiperbolik fonksiyonları kullanmanın avantajları, Taylor ve Wheeler'ın klasik kitapları gibi bazı ders kitaplarında bunların kullanımının çok erken bir aşamada tanıtılmasına neden olmuştur. ⓘ
4-vektörler
Dört vektörlerden yukarıda enerji-momentum 4-vektörü bağlamında bahsedilmişti, ancak üzerinde fazla durulmamıştı. Aslında, özel göreliliğin temel türevlerinden hiçbiri bunları gerektirmez. Ancak bir kez anlaşıldığında, 4-vektörler ve daha genel olarak tensörler, özel göreliliğin matematiğini ve kavramsal anlayışını büyük ölçüde basitleştirir. Yalnızca bu tür nesnelerle çalışmak, açıkça göreli olarak değişmez olan formüllere yol açar ki bu da önemsiz olmayan bağlamlarda önemli bir avantajdır. Örneğin, Maxwell denklemlerinin olağan haliyle göreli değişmezliğini göstermek önemsiz değildir, ancak alan kuvveti tensör formülasyonu kullanılarak sadece rutin bir hesaplama (aslında bir gözlemden daha fazlası değil) yapılabilir. Öte yandan, genel görelilik, en başından beri, fiziksel olarak ilgili varlıkları temsil eden 4-vektörlere ve daha genel olarak tensörlere dayanır. Bunları belirli koordinatlara dayanmayan denklemler aracılığıyla ilişkilendirmek, özel görelilikte olduğu gibi sadece düz bir uzayda değil, eğri bir uzayda bile bu tür 4-vektörleri birbirine bağlayabilen tensörler gerektirir. Tensörlerin incelenmesi bu makalenin kapsamı dışındadır ve sadece uzayzamanla ilgili temel bir tartışma sunmaktadır. ⓘ
4-vektörlerin tanımı
4'lü bir çift, Ai bileşeni çerçeveler arasında Lorentz dönüşümüne göre dönüşüyorsa bir "4-vektör "dür. ⓘ
Eğer kullanılıyorsa koordinatlarına göre (x yönünde) dönüşüyorsa, A bir 4-vektördür.
Bu da Lorentz dönüşümünün önceki sunumunda ct'nin A0 ve x'in A1 ile değiştirilmesinden gelir. ⓘ
Her zamanki gibi, x, t, vb. yazdığımızda genellikle Δx, Δt vb. anlamına gelir. ⓘ
Bir 4-vektörün son üç bileşeni üç boyutlu uzayda standart bir vektör olmalıdır. Bu nedenle, bir 4-vektör şu şekilde dönüşmelidir Lorentz dönüşümlerinin yanı sıra rotasyonlar altında da. ⓘ
4-vektörlerin özellikleri
- Doğrusal kombinasyon altında kapanış: Eğer A ve B 4 vektörlü ise, o zaman aynı zamanda bir 4-vektördür.
- İç çarpım değişmezliği: Eğer A ve B 4-vektör ise, iç çarpımları (skaler çarpım) değişmezdir, yani iç çarpımları hesaplandığı çerçeveden bağımsızdır. İç çarpımın hesaplanmasının 3-vektörün iç çarpımının hesaplanmasından nasıl farklı olduğuna dikkat edin. Aşağıda, ve 3-vektörlerdir:
- Lorentz dönüşümü altında değişmez olmasının yanı sıra, yukarıdaki iç çarpım 3 uzayında dönme altında da değişmezdir.
- Aşağıdaki durumlarda iki vektörün ortogonal olduğu söylenir Ortogonal 4-vektörler, 3-vektörlerin aksine birbirleriyle dik açı yapmak zorunda değildir. Kural, iki 4-vektörün, bir ışık ışınının dünya doğrusu olan 45° doğrusundan eşit ve zıt açılarla sapmaları halinde ortogonal olmalarıdır. Bu, ışık benzeri bir 4-vektörün kendisiyle ortogonal olduğu anlamına gelir.
- Bir vektörün büyüklüğünün değişmezliği: Bir vektörün büyüklüğü, bir 4-vektörün kendisiyle iç çarpımıdır ve çerçeveden bağımsız bir özelliktir. Aralıklarda olduğu gibi, büyüklük pozitif, negatif veya sıfır olabilir, böylece vektörler zaman benzeri, uzay benzeri veya null (ışık benzeri) olarak adlandırılır. Boş vektörün sıfır vektörle aynı şey olmadığını unutmayın. Boş bir vektör, aşağıdakilerden biridir sıfır vektör ise tüm bileşenleri sıfır olan bir vektördür. Normun değişmezliğini gösteren özel durumlar, değişmez aralığı içerir ve rölativistik momentum vektörünün değişmez uzunluğu ⓘ
4-vektör örnekleri
- Yer değiştirme 4-vektörü: Uzay-zaman ayrımı olarak da bilinen bu vektör (Δt, Δx, Δy, Δz) ya da sonsuz küçük ayrımlar için (dt, dx, dy, dz) şeklindedir.
- Hız 4-vektörü: Bu, yer değiştirme 4-vektörü aşağıdakilere bölündüğünde ortaya çıkar , nerede dt, dx, dy ve dz değerlerini veren iki olay arasındaki uygun zamandır.
- 4-hız bir parçacığın dünya çizgisine teğettir ve parçacığın çerçevesinde bir birim zamana eşit bir uzunluğa sahiptir.
- Hızlandırılmış bir parçacığın her zaman hareketsiz olduğu bir eylemsiz çerçevesi yoktur. Ancak, parçacıkla anlık olarak aynı doğrultuda hareket eden bir eylemsiz çerçeve her zaman bulunabilir. Bu çerçeve, anlık hareket eden referans çerçevesi (MCRF), özel göreliliğin hızlandırılmış parçacıkların analizine uygulanmasını sağlar.
- Fotonlar boş çizgiler üzerinde hareket ettiğinden, bir foton için 4-hız tanımlanamaz. Bir fotonun hareketsiz olduğu bir çerçeve yoktur ve bir fotonun yolu boyunca hiçbir MCRF oluşturulamaz.
- Enerji-momentum 4-vektörü:
- Daha önce de belirtildiği gibi, enerji-momentum 4-vektörü için farklı uygulamalar vardır, bu nedenle şu şekilde ifade edildiği de görülebilir veya İlk bileşen, belirli bir çerçevedeki parçacığın (veya parçacık sisteminin) toplam enerjisidir (kütle dahil), diğer bileşenler ise uzaysal momentumudur. Enerji-momentum 4-vektörü korunmuş bir niceliktir.
- İvme 4-vektörü: Bu, hız 4-vektörünün aşağıdakilere göre türevinin alınmasından kaynaklanır
- Kuvvet 4-vektörü: Bu, momentum 4-vektörünün aşağıdakilere göre türevidir
Beklendiği gibi, yukarıdaki 4-vektörün son bileşenlerinin tümü uzaysal 3-momentum, 3-kuvvet vb.ne karşılık gelen standart 3-vektörlerdir. ⓘ
4-vektörler ve fizik yasası
Özel göreliliğin ilk önermesi tüm eylemsiz çerçevelerin eşdeğerliğini ilan eder. Bir çerçevede geçerli olan bir fiziksel yasa tüm çerçevelerde geçerli olmalıdır, aksi takdirde çerçeveler arasında ayrım yapmak mümkün olurdu. Newton momentumları Lorentzian dönüşümü altında düzgün davranamaz ve Einstein momentumun korunumundan vazgeçmek yerine momentum tanımını 4-vektör içeren bir tanıma dönüştürmeyi tercih etmiştir. ⓘ
Fiziksel yasalar çerçeveden bağımsız yapılara dayanmalıdır. Bu, fiziksel yasaların her zaman çerçeveden bağımsız olan skalerleri bağlayan denklemler biçimini alabileceği anlamına gelir. Bununla birlikte, 4-vektörleri içeren denklemler, uygun rütbeye sahip tensörlerin kullanılmasını gerektirir ve bunlar da 4-vektörlerden oluşturulmuş olarak düşünülebilir. ⓘ
İvme
Özel göreliliğin yalnızca eylemsiz çerçeveler için geçerli olduğu ve ivmelenen nesneleri ya da ivmelenen referans çerçevelerini ele alamayacağı yaygın bir yanılgıdır. Aslında, ivmelenen nesneler genellikle ivmelenen çerçevelerle hiç uğraşmaya gerek kalmadan analiz edilebilir. Sadece kütle çekimi önemli olduğunda genel göreliliğe ihtiyaç duyulur. ⓘ
Bununla birlikte, ivmelenen çerçeveleri düzgün bir şekilde ele almak biraz dikkat gerektirir. Özel ve genel görelilik arasındaki fark şudur: (1) Özel görelilikte tüm hızlar görelidir, ancak ivme mutlaktır. (2) Genel görelilikte, ister eylemsiz, ister ivmeli, isterse de dönen olsun, tüm hareketler görelidir. Bu farklılığa uyum sağlamak için genel görelilik eğri uzayzaman kullanır. ⓘ
Bu bölümde, hızlandırılmış referans çerçevelerini içeren çeşitli senaryoları analiz ediyoruz. ⓘ
Dewan-Beran-Bell uzay gemisi paradoksu
Dewan-Beran-Bell uzay gemisi paradoksu (Bell'in uzay gemisi paradoksu), uzay-zaman yaklaşımının geometrik kavrayışından destek almayan sezgisel akıl yürütmenin sorunlara yol açabileceği bir probleme iyi bir örnektir. ⓘ

Şekil 4-4'te, iki özdeş uzay gemisi uzayda yüzmekte ve birbirlerine göre hareketsiz durumdadır. Kopmadan önce yalnızca sınırlı miktarda esneme kapasitesine sahip bir sicimle bağlıdırlar. Gözlemci çerçevesi olan bizim çerçevemizde belirli bir anda, her iki uzay gemisi de aralarındaki çizgi boyunca aynı sabit uygun ivmeyle aynı yönde hızlanmaktadır. İp kopacak mı? ⓘ
Paradoks yeni ve nispeten bilinmezken, profesyonel fizikçiler bile çözümü bulmakta zorlanmışlardır. İki akıl yürütme çizgisi zıt sonuçlara götürmektedir. Aşağıda sunulan her iki argüman da, içlerinden biri doğru cevabı verse de, kusurludur.
- Dinlenme çerçevesindeki gözlemciler için uzay gemileri birbirlerinden L uzaklıkta başlar ve hızlanma sırasında aynı uzaklıkta kalırlar. Hızlanma sırasında L, hızlanan uzay gemilerinin çerçevesindeki L' = γL mesafesinin uzunlukça daralmış bir mesafesidir. Yeterince uzun bir süre sonra γ, ipin kopmasını gerektirecek kadar büyük bir faktöre yükselecektir.
- A ve B arka ve ön uzay gemileri olsun. Uzay gemilerinin çerçevesi içinde, her uzay gemisi diğer uzay gemisinin kendisiyle aynı şeyi yaptığını görür. A, B'nin kendisiyle aynı ivmeye sahip olduğunu söyler ve B, A'nın her hareketine uyduğunu görür. Böylece uzay gemileri birbirlerinden aynı uzaklıkta kalır ve ip kopmaz. ⓘ
İlk argümanla ilgili sorun, "uzay gemilerinin çerçevesi" diye bir şeyin olmamasıdır. Olamaz, çünkü iki uzay gemisi arasında giderek artan bir mesafe ölçülür. Uzay gemilerinin ortak bir çerçevesi olmadığından, ipin uzunluğu tanımsızdır. Yine de sonuç doğrudur ve argüman çoğunlukla doğrudur. Ancak ikinci argüman, eşzamanlılığın göreliliğini tamamen göz ardı eder. ⓘ
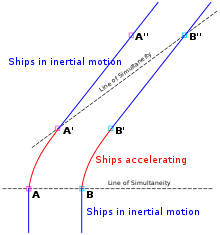
Bir uzay-zaman diyagramı (Şekil 4-5) bu paradoksun doğru çözümünü hemen ortaya koyar. Minkowski uzayzamanındaki iki gözlemci sabit büyüklükte ivmelenir uygun zaman için hızlanma (ivme ve geçen zaman gözlemcilerin kendileri tarafından ölçülür, eylemsiz bir gözlemci tarafından değil). Bu aşamadan önce ve sonra eşzamanlı ve eylemsizdirler. Minkowski geometrisinde, eşzamanlılık çizgisi boyunca uzunluk eşzamanlılık çizgisi boyunca uzunluktan daha büyük olduğu ortaya çıkar . ⓘ
Uzunluk artışı Lorentz dönüşümü yardımıyla hesaplanabilir. Eğer, Şekil 4-5'te gösterildiği gibi, ivmelenme tamamlanırsa, gemiler bazı çerçevelerde sabit bir ofsette kalacaktır Eğer ve gemilerin konumlarıdır. çerçevedeki pozisyonlar vardır:
"Paradoks", Bell'in örneğini kurgulama biçiminden kaynaklanmaktadır. Lorentz büzülmesinin olağan tartışmasında, durgun uzunluk sabittir ve hareketli uzunluk aşağıdaki çerçevede ölçüldüğü gibi kısalır . Şekil 4-5'te gösterildiği gibi, Bell'in örneği hareketli uzunlukların ve çerçeve içinde ölçülür sabit olması için, böylece dinlenme çerçevesi uzunluğunu çerçeve içinde artacak. ⓘ
Ufuklu hızlandırılmış gözlemci
Bazı özel görelilik problem düzenekleri, olay ufukları gibi normalde genel görelilikle ilişkilendirilen olgular hakkında fikir verebilir. Şekil 2-7'ye eşlik eden metinde, eflatun hiperboller uzayzamanda sürekli hızlanan bir yolcunun izlediği gerçek yolları temsil etmektedir. Pozitif ivmelenme dönemlerinde, yolcunun hızı ışık hızına yaklaşırken, bizim çerçevemizde ölçüldüğünde, yolcunun ivmesi sürekli olarak azalır. ⓘ
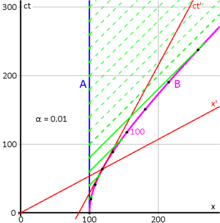
Şekil 4-6 yolcunun hareketlerinin çeşitli özelliklerini daha belirgin bir şekilde detaylandırmaktadır. Herhangi bir anda, uzay ekseni orijinden ve hiperbol üzerindeki mevcut konumundan geçen bir doğru tarafından oluşturulurken, zaman ekseni hiperbolün kendi konumundaki teğetidir. Hız parametresi bir sınırına yaklaştıkça artar. Aynı şekilde, sonsuza yaklaşır. ⓘ
Değişmez hiperbolün şekli, sabit düzgün ivmeli bir yola karşılık gelir. Bu aşağıdaki şekilde gösterilebilir:
- Hatırlayalım ki
- O zamandan beri şu sonuca varıyoruz
- Rölativistik kuvvet yasasından,
- Değiştirme için 2. adımdaki ifade ve 3. adımdan itibaren Bu da sabit bir ifadedir. ⓘ
Şekil 4-6 hesaplanmış belirli bir senaryoyu göstermektedir. Terence (A) ve Stella (B) başlangıçta orijinden 100 ışık saati uzaklıkta birlikte durmaktadır. Stella 0 zamanında havalanır, uzay aracı saatte 0.01 c hızlanmaktadır. Terence her yirmi saatte bir Stella'ya evdeki durumla ilgili güncellemeler gönderir (düz yeşil çizgiler). Stella bu düzenli iletileri alır, ancak artan mesafe (kısmen zaman genişlemesi ile dengelenir) Terence'ın iletişimlerini kendi saatinde ölçüldüğü gibi daha geç almasına neden olur ve Terence'ın saatinde 100 saatten sonra ondan hiç iletişim almaz (kesikli yeşil çizgiler). ⓘ
Terence'ın saatine göre 100 saat sonra Stella karanlık bir bölgeye girer. Terence'ın zaman benzeri geleceğinin dışına çıkmıştır. Öte yandan, Terence Stella'nın kendisine gönderdiği mesajları sonsuza dek almaya devam edebilir. Sadece yeterince uzun süre beklemesi gerekir. Uzayzaman görünür bir olay ufku ile ayrılmış farklı bölgelere bölünmüştür. Stella hızlanmaya devam ettiği sürece, bu ufkun arkasında neler olduğunu asla bilemez. ⓘ
Eğri uzay-zamana giriş
Temel önermeler
Newton'un teorileri, hareketin tüm uzay ve tüm zaman boyunca uzanan katı bir Öklid referans çerçevesi zemininde gerçekleştiğini varsayıyordu. Yerçekimine, bir mesafe boyunca anlık olarak etki eden ve eylemleri araya giren uzaydan bağımsız olan gizemli bir kuvvet aracılık eder. Buna karşılık Einstein, uzay boyunca uzanan herhangi bir arka plan Öklid referans çerçevesi olduğunu reddetmiştir. Kütle çekim kuvveti diye bir şey de yoktur, sadece uzayzamanın yapısı vardır. ⓘ

Uzay-zaman terimleriyle, Dünya'nın yörüngesinde dönen bir uydunun yolu Dünya, Ay ve Güneş'in uzak etkileri tarafından belirlenmez. Bunun yerine, uydu uzayda yalnızca yerel koşullara tepki olarak hareket eder. Yeterince küçük bir ölçekte düşünüldüğünde uzayzaman her yerde yerel olarak düz olduğundan, uydu kendi yerel eylemsizlik çerçevesinde her zaman düz bir çizgi izler. Uydunun her zaman bir jeodezik yol boyunca ilerlediğini söyleriz. Tek bir parçacığın hareketlerini takip ederek kütle çekimine dair hiçbir kanıt bulunamaz. ⓘ
Uzayzamanın herhangi bir analizinde, kütleçekiminin kanıtı iki cismin ya da iki ayrı parçacığın göreli ivmelerinin gözlemlenmesini gerektirir. Şekil 5-1'de, Dünya'nın kütleçekim alanında serbest düşüş yapan iki ayrı parçacık, kütleçekim alanındaki yerel homojensizliklerden dolayı gelgit ivmeleri sergiler, öyle ki her parçacık uzay-zamanda farklı bir yol izler. Bu parçacıkların birbirlerine göre sergiledikleri gelgit ivmeleri, açıklamaları için kuvvet gerektirmez. Einstein bunları daha ziyade uzayzamanın geometrisi, yani uzayzamanın eğriliği açısından tanımlamıştır. Bu gelgit ivmeleri kesinlikle yereldir. Dünya'dan uzun bir mesafede etki eden bir yerçekimi kuvvetinin ortaya çıkmasına neden olan, eğriliğin birçok yerel tezahürünün kümülatif toplam etkisidir. ⓘ
Genel göreliliğin altında iki temel önerme yatar.
- İlk önemli kavram koordinat bağımsızlığıdır: Fizik yasaları, kişinin hangi koordinat sistemini kullandığına bağlı olamaz. Bu, fizik yasalarının ivmesiz (eylemsiz) referans çerçevelerinde hareket eden her gözlemci için aynı olması gerektiğini belirten özel görelilikte kullanılan versiyondan görelilik ilkesinin önemli bir uzantısıdır. Genel görelilikte, Einstein'ın kendi (tercüme edilmiş) sözlerini kullanırsak, "fizik yasaları öyle bir yapıda olmalıdır ki, her türlü hareket halindeki referans sistemlerine uygulanabilmelidir." Bu da acil bir soruna yol açmaktadır: İvmelendirilmiş çerçevelerde, kişi görünüşte ivmelenme durumunu mutlak anlamda değerlendirmesini sağlayacak kuvvetler hisseder. Einstein bu sorunu eşdeğerlik ilkesi aracılığıyla çözmüştür. ⓘ

- Eşdeğerlik ilkesi, uzayın yeterince küçük herhangi bir bölgesinde, yerçekiminin etkilerinin ivmeden kaynaklanan etkilerle aynı olduğunu belirtir.
- Şekil 5-2'de A kişisi, herhangi bir kütleli nesneden uzakta, g kadar düzgün bir ivmeye maruz kalan bir uzay gemisindedir. Uzay gemisinin gelgit etkilerinin ölçülemeyeceği kadar küçük olması koşuluyla (mevcut yerçekimi ölçüm cihazlarının hassasiyeti göz önüne alındığında, A ve B muhtemelen Lilliput'lular olmalıdır), A ve B'nin hangi ortamda olduklarını söyleyebilecekleri hiçbir deney yoktur.
- Eşdeğerlik ilkesinin alternatif bir ifadesi, Newton'un evrensel çekim yasasında F = GMmg/r2 = mgg ve Newton'un ikinci yasasında F = mia, yerçekimsel kütle mg'nin eylemsiz kütle mi'ye eşit olması için a priori bir neden olmadığını belirtmektir. Eşdeğerlik ilkesi bu iki kütlenin özdeş olduğunu belirtir. ⓘ
Eğri uzayzamanın yukarıdaki temel tanımından kütleçekiminin tam bir tanımına geçmek için tensör hesabı ve diferansiyel geometri gerekir, her ikisi de önemli ölçüde çalışma gerektiren konulardır. Bu matematiksel araçlar olmadan, genel görelilik hakkında yazmak mümkündür, ancak önemsiz olmayan türevleri göstermek mümkün değildir. ⓘ
Zaman eğriliği

Özel görelilik tartışmasında kuvvetler arka planda bir rol oynamaktan öteye gidememiştir. Özel görelilik, tüm uzayzamanı dolduran ve tüm saatleri orijindeki saatle aynı hızda çalışan eylemsiz çerçeveler tanımlama yeteneğini varsayar. Bu gerçekten mümkün müdür? Düzgün olmayan bir kütleçekim alanında deneyler cevabın hayır olduğunu göstermektedir. Kütleçekim alanları küresel bir eylemsiz çerçeve oluşturmayı imkansız kılar. Uzayzamanın yeterince küçük bölgelerinde, yerel eylemsiz çerçeveler hala mümkündür. Genel görelilik, bu yerel çerçevelerin sistematik olarak bir araya getirilerek daha genel bir uzay-zaman resmine dönüştürülmesini içerir. ⓘ
Genel teorinin 1916'da yayınlanmasından yıllar önce, Einstein aşağıdaki düşünce deneyinde kütleçekimsel kırmızıya kaymanın varlığını tahmin etmek için eşdeğerlik ilkesini kullanmıştır: (i) h yüksekliğinde bir kule (Şekil 5-3) inşa edildiğini varsayın. (ii) Durgun kütlesi m olan bir parçacığı kulenin tepesinden bırakın. Parçacık g ivmesiyle serbestçe düşerek v = (2gh)1/2 hızıyla yere ulaşır, böylece yerdeki bir gözlemci tarafından ölçülen toplam enerjisi E (iii) Bir kütle-enerji dönüştürücüsü parçacığın toplam enerjisini yukarı doğru yönlendirdiği tek bir yüksek enerjili fotona dönüştürür. (iv) Kulenin tepesinde, bir enerji-kütle dönüştürücü foton E' enerjisini tekrar durgun kütle m' parçacığına dönüştürür. ⓘ
Bu m = m' olmalıdır, çünkü aksi takdirde sürekli hareket eden bir cihaz inşa etmek mümkün olurdu. Bu nedenle E' = m olduğunu tahmin ediyoruz, böylece
Dünya'nın yerçekimi alanına tırmanan bir foton enerji kaybeder ve kırmızıya kayar. Bu kırmızıya kaymayı astronomik gözlemler yoluyla ölçmeye yönelik ilk girişimler biraz sonuçsuz kalmıştır, ancak kesin laboratuvar gözlemleri Pound & Rebka (1959) ve daha sonra Pound & Snider (1964) tarafından gerçekleştirilmiştir. ⓘ
Işığın ilişkili bir frekansı vardır ve bu frekans bir saatin çalışmasını sağlamak için kullanılabilir. Kütleçekimsel kırmızıya kayma zamanın kendisi hakkında önemli bir sonuca götürür: Yerçekimi zamanın daha yavaş akmasına neden olur. Hızları bazı kararlı atomik geçişler tarafından kontrol edilen iki özdeş saat inşa ettiğimizi varsayalım. Saatlerden birini kulenin tepesine yerleştirelim, diğer saat ise yerde kalsın. Kulenin tepesindeki bir deneyci yerdeki saatten gelen sinyallerin frekansının kulede yanındaki saatten gelen sinyallerden daha düşük olduğunu gözlemler. Kuleye çıkan ışık sadece bir dalgadır ve dalga tepelerinin yukarı çıkarken kaybolması imkansızdır. Kulenin tepesine tam olarak en altta yayılan kadar ışık salınımı ulaşır. Deneyci yer saatinin yavaş çalıştığı sonucuna varır ve kule saatini yer saatiyle yan yana karşılaştırmak için aşağı indirerek bunu doğrulayabilir. 1 km'lik bir kule için tutarsızlık günde yaklaşık 9,4 nanosaniyedir ve modern aletlerle kolayca ölçülebilir. ⓘ
Yerçekimi alanındaki saatlerin hepsi aynı hızda çalışmaz. Pound-Rebka deneyi gibi deneyler uzay-zamanın zaman bileşeninin eğriliğini kesin olarak ortaya koymuştur. Pound-Rebka deneyi uzay-zamanın uzay bileşeninin eğriliği hakkında hiçbir şey söylemez. Ancak kütleçekimsel zaman genişlemesini öngören teorik argümanlar genel göreliliğin ayrıntılarına hiç bağlı değildir. Herhangi bir kütleçekim teorisi, eşdeğerlik ilkesine uyduğu takdirde kütleçekimsel zaman genişlemesini öngörecektir. Buna Newton kütle çekimi de dahildir. Genel görelilikteki standart bir gösterim, "Newton limitinde" (yani parçacıklar yavaş hareket ediyor, yerçekimi alanı zayıf ve alan statik), Newton'un yerçekimi yasasını türetmek için tek başına zaman eğriliğinin nasıl yeterli olduğunu göstermektir. ⓘ
Newton kütle çekimi bir eğri zaman teorisidir. Genel görelilik ise bir eğri zaman ve eğri uzay teorisidir. Yerçekimi sabiti olarak G, Newton yıldızının kütlesi olarak M ve yıldızdan r uzaklığında yörüngede dönen önemsiz kütleli cisimler göz önüne alındığında, Newton kütleçekimi için uzay-zaman aralığı, yalnızca zaman katsayısının değişken olduğu bir aralıktır:
Uzay eğriliği
Bu önündeki katsayı Newton kütleçekiminde zamanın eğriliğini tanımlar ve bu eğrilik tüm Newton kütleçekim etkilerini tamamen açıklar. Beklendiği gibi, bu düzeltme faktörü aşağıdakilerle doğru orantılıdır ve ve bu nedenle paydada, yerçekimi yapan cisme yaklaştıkça düzeltme faktörü artar, bu da zamanın eğrildiği anlamına gelir. ⓘ
Ancak genel görelilik bir eğri uzay ve eğri zaman teorisidir, bu nedenle yukarıda sunulan uzay-zaman aralığının uzaysal bileşenlerini değiştiren terimler varsa, uzaysal terimlere uygulanan eğrilik düzeltme faktörleri nedeniyle bunların etkilerinin örneğin gezegen ve uydu yörüngelerinde görülmesi gerekmez mi? ⓘ
Cevap, bunların görüldüğü, ancak etkilerinin çok küçük olduğudur. Bunun nedeni, gezegen hızlarının ışık hızına kıyasla son derece küçük olmasıdır, böylece güneş sistemindeki gezegenler ve uydular için terimi uzaysal terimleri cüceleştirir. ⓘ
Uzaysal terimlerin küçüklüğüne rağmen, Newton kütle çekiminde bir şeylerin yanlış olduğuna dair ilk işaretler bir buçuk asır önce keşfedilmiştir. 1859 yılında Urbain Le Verrier, 1697'den 1848'e kadar Merkür'ün Güneş diski üzerindeki geçişlerinin mevcut zamanlı gözlemlerinin bir analizinde, Merkür'ün yörüngesinde muhtemelen bir gezegen veya asteroit kuşağı olmadığı sürece bilinen fiziğin Merkür'ün yörüngesini açıklayamayacağını bildirdi. Merkür'ün yörüngesinin perihelion'u, diğer gezegenlerin çekimleriyle açıklanabilecek olandan daha fazla bir presesyon oranı sergilemiştir. Bu anormal presesyonun dakikalık değerini (tropik yüzyıl başına sadece 43 yay saniyesi) tespit etme ve doğru bir şekilde ölçme yeteneği, 19. yüzyıl astrometrisinin gelişmişliğinin bir kanıtıdır. ⓘ

Daha önce Uranüs'ün yörüngesindeki yalpalamaları analiz ederek Neptün'ün varlığını "kaleminin ucuyla" keşfetmiş olan ünlü astronom Le Verrier'in duyurusu, profesyonel ve amatör astronomların varsayımsal yeni gezegenin peşine düştüğü yirmi yıllık bir "Vulcan-mania" dönemini tetikledi. Bu arayış Vulcan'ın birkaç kez yanlış görülmesini de içeriyordu. Nihayetinde böyle bir gezegen ya da asteroit kuşağının var olmadığı tespit edildi. ⓘ
1916'da Einstein, Merkür'ün bu anormal presesyonunun uzay-zamanın eğriliğindeki uzaysal terimlerle açıklandığını gösterecekti. Zamansal terimdeki eğrilik, sadece Newton kütleçekiminin bir ifadesi olarak, bu anormal presesyonun açıklanmasında hiçbir role sahip değildir. Hesaplamasının başarısı Einstein'ın meslektaşları için genel görelilik kuramının doğru olabileceğinin güçlü bir göstergesiydi. ⓘ
Einstein'ın tahminleri arasında en dikkat çekici olanı, uzay-zaman aralığının uzaysal bileşenlerindeki eğrilik terimlerinin, ışığın büyük bir cisim etrafındaki bükülmesinde ölçülebileceğini hesaplamasıydı. Işığın uzay-zaman diyagramında ±1'lik bir eğimi vardır. Uzaydaki hareketi zamandaki hareketine eşittir. Einstein, değişmez aralığın zayıf alan ifadesi için, uzaysal bileşenlerinde tam olarak eşit ama zıt işaretli bir eğrilik hesaplamıştır.
Newton'un kütle çekiminde önündeki katsayı ışığın bir yıldızın etrafında bükülmesini öngörür. Genel görelilikte önündeki katsayı toplam bükülmenin iki katına çıkacağını öngörür. ⓘ
1919 Eddington tutulma keşif gezisinin ve Einstein'ın üne kavuşmasının öyküsü başka yerlerde de anlatılmaktadır. ⓘ
Uzay-zaman eğriliğinin kaynakları

Newton'un yerçekimi teorisinde, yerçekimi kuvvetinin tek kaynağı kütledir. ⓘ
Buna karşılık genel görelilik, kütleye ek olarak uzay-zaman eğriliğinin çeşitli kaynaklarını tanımlar. Einstein alan denklemlerinde, 'de sağ tarafta yerçekimi kaynakları sunulmaktadır. stres-enerji tensörü. ⓘ
Şekil 5-5 stres-enerji tensöründeki çeşitli yerçekimi kaynaklarını sınıflandırmaktadır:
- (kırmızı): Toplam kütle-enerji yoğunluğu, parçacıklar arasındaki kuvvetlerden kaynaklanan potansiyel enerjiye herhangi bir katkının yanı sıra rastgele termal hareketlerden kaynaklanan kinetik enerji de dahil olmak üzere.
- ve (turuncu): Bunlar momentum yoğunluğu terimleridir. Yığın hareketi olmasa bile, enerji ısı iletimi yoluyla aktarılabilir ve iletilen enerji momentum taşıyacaktır.
- j-yönünde birim alan başına momentumun i-bileşeninin akış oranlarıdır. Yığın hareketi olmasa bile, parçacıkların rastgele termal hareketleri momentum akışına yol açacaktır, bu nedenle i = j terimleri (yeşil) izotropik basıncı ve i ≠ j terimleri (mavi) kayma gerilmelerini temsil eder. ⓘ
Denklemlerden çıkarılabilecek önemli bir sonuç, halk dilinde yerçekiminin kendisinin yerçekimi yarattığıdır. Enerjinin kütlesi vardır. Newton yerçekiminde bile, yerçekimi alanı bir enerji ile ilişkilidir, Kütleçekimsel potansiyel enerji olarak adlandırılır. Genel görelilikte, kütleçekim alanının enerjisi, kütleçekim alanının yaratılmasına geri beslenir. Bu da denklemleri doğrusal olmayan ve zayıf alan durumları dışında çözülmesi zor hale getirir. Sayısal görelilik, problemleri çözmek ve analiz etmek için sayısal yöntemler kullanan, genellikle kara delikleri, yerçekimi dalgalarını, nötron yıldızlarını ve güçlü alan rejimindeki diğer olayları incelemek için süper bilgisayarları kullanan bir genel görelilik dalıdır. ⓘ
Enerji-momentum
Özel görelilikte kütle-enerji momentumla yakından bağlantılıdır. Tıpkı uzay ve zamanın uzay-zaman adı verilen daha kapsamlı bir varlığın farklı yönleri olması gibi, kütle-enerji ve momentum da dört-momentum adı verilen birleşik, dört-boyutlu bir niceliğin farklı yönleridir. Sonuç olarak, eğer kütle-enerji kütleçekiminin bir kaynağı ise, momentum da bir kaynak olmalıdır. Momentumun bir yerçekimi kaynağı olarak dahil edilmesi, hareket eden veya dönen kütlelerin, gravitomanyetizma olarak bilinen bir olgu olan hareketli yükler tarafından üretilen manyetik alanlara benzer alanlar oluşturabileceği tahminine yol açar. ⓘ

Manyetizma kuvvetinin, özel görelilik kurallarının hareketli yüklere uygulanmasıyla çıkarılabileceği iyi bilinmektedir. (Feynman bunun güzel bir gösterimini Fizik Dersleri'nin II. cilt, 13-6. bölümünde sunmuştur, internetten erişilebilir). Benzer mantık gravitomanyetizmanın kökenini göstermek için de kullanılabilir. Şekil 5-7a'da, iki paralel, sonsuz uzunlukta kütleli parçacık akımı, ikisi arasında ortalanmış ve hareketsiz duran bir test parçacığına göre eşit ve zıt -v ve +v hızlarına sahiptir. Düzenin simetrisi nedeniyle, test parçacığı üzerindeki net kuvvet merkezi parçacık sıfırdır. Varsayalım ki böylece hızlar basitçe birbirine eklenir. Şekil 5-7b'de tam olarak aynı düzenek gösterilmektedir, ancak üst akış çerçevesinde. Test parçacığının hızı +v ve alt akışın hızı +2v'dir. Fiziksel durum değişmediğinden, sadece olayların gözlemlendiği çerçeve değiştiğinden, test parçacığı her iki akıma da doğru çekilmemelidir. Ancak test parçacığı üzerine uygulanan kuvvetlerin eşit olduğu hiç de açık değildir. (1) Alttaki akım üsttekinden daha hızlı hareket ettiğinden, alttaki akımdaki her bir parçacık üstteki bir parçacıktan daha büyük bir kütle enerjisine sahiptir. (2) Lorentz daralması nedeniyle, alttaki akımda birim uzunluk başına üstteki akımdan daha fazla parçacık vardır. (3) Alt akımın aktif kütleçekimsel kütlesine bir başka katkı da, bu noktada tartışmak için yeterli arka plana sahip olmadığımız ek bir basınç teriminden gelir. Tüm bu etkiler birlikte test parçacığının alt akıma doğru çekilmesini gerektirmektedir. ⓘ
Test parçacığı, alt akımla aynı yönde hareket eden bir parçacığı itmeye yarayan hıza bağlı bir kuvvet nedeniyle alt akıma doğru çekilmez. Bu hıza bağlı yerçekimi etkisi gravitomanyetizmadır. ⓘ
Dolayısıyla, bir gravitomanyetik alan boyunca hareket halindeki madde, elektromanyetik indüksiyona benzer çerçeve sürükleme etkilerine maruz kalır. Dönen bazı süper kütleli kara delikler tarafından fırlatılan rölativistik jetlerin (Şekil 5-8) oluşumunun altında bu tür gravitomanyetik kuvvetlerin yattığı öne sürülmüştür. ⓘ
Basınç ve stres
Enerji ve momentumla doğrudan ilişkili olan nicelikler, yani iç basınç ve stres de yerçekimi kaynağı olmalıdır. Birlikte ele alındığında, kütle-enerji, momentum, basınç ve stresin hepsi yerçekimi kaynağı olarak hizmet eder: Hepsi birlikte uzayzamana nasıl eğilmesi gerektiğini söyler. ⓘ
Genel görelilik, basıncın kütle-enerji yoğunluğu ile tam olarak aynı güçte bir çekim kaynağı olarak hareket ettiğini öngörür. Basıncın bir kütleçekim kaynağı olarak dahil edilmesi, genel göreliliğin tahminleri ile Newton kütleçekiminin tahminleri arasında dramatik farklılıklara yol açar. Örneğin, basınç terimi bir nötron yıldızının kütlesine maksimum bir sınır koyar. Bir nötron yıldızı ne kadar büyükse, yerçekimine karşı ağırlığını desteklemek için o kadar fazla basınç gerekir. Ancak artan basınç, yıldızın kütlesine etki eden yerçekimine katkıda bulunur. Tolman-Oppenheimer-Volkoff limiti tarafından belirlenen belirli bir kütlenin üzerinde, süreç kaçak hale gelir ve nötron yıldızı bir kara deliğe çöker. ⓘ
Çekirdek çökmesi süpernovalarının hidrodinamik simülasyonları gibi hesaplamalar yapılırken stres terimleri oldukça önemli hale gelir. ⓘ
Uzay-zaman eğriliğinin kaynakları olarak basınç, momentum ve stresin rollerine ilişkin bu tahminler zariftir ve teoride önemli bir rol oynamaktadır. Basınçla ilgili olarak, erken evren radyasyon baskındı ve eğer basınç kütleçekimine katkıda bulunmasaydı ya da kütleçekimi kaynağı olarak kütle-enerji ile aynı güce sahip olmasaydı, ilgili kozmolojik verilerin (örneğin nükleosentez bollukları, vb.) herhangi birinin yeniden üretilmesi pek olası değildir. Benzer şekilde, Einstein alan denklemlerinin matematiksel tutarlılığı, stres terimlerinin bir yerçekimi kaynağı olarak katkıda bulunmaması durumunda bozulacaktır. ⓘ
Uzay-zaman eğriliğinin kaynaklarının deneysel testi
Tanımlar: Aktif, pasif ve eylemsiz kütle
Bondi farklı olası kütle türleri arasında ayrım yapar: (1) aktif kütle () yerçekimi alanının kaynağı olarak hareket eden kütledir; (2) pasif kütle () yerçekimi alanına tepki veren kütledir; (3) eylemsizlik kütlesi () ivmeye tepki veren kütledir. ⓘ
- yerçekimsel kütle ile aynıdır () eşdeğerlik ilkesinin tartışılmasında. ⓘ
Newton teorisinde,
- Üçüncü etki-tepki yasasına göre ve aynı olmalıdır.
- Öte yandan, ister ve eşit olması ampirik bir sonuçtur. ⓘ
Genel görelilikte,
- Eşitlik ve eşdeğerlik ilkesi tarafından belirlenir.
- "Etki ve tepki" ilkesi, aşağıdakiler arasında gerekli herhangi bir ilişkiyi dikte etmez ve . ⓘ
Yerçekimi kaynağı olarak basınç

Bir yerçekimi kaynağının gücünü (yani aktif kütlesini) ölçmek için yapılan klasik deney ilk olarak 1797 yılında Henry Cavendish tarafından gerçekleştirilmiştir (Şekil 5-9a). İki küçük ama yoğun top ince bir tel üzerine asılarak bir burulma dengesi oluşturulur. İki büyük test kütlesinin toplara yaklaştırılması tespit edilebilir bir tork yaratır. Cihazın boyutları ve burulma telinin ölçülebilir yay sabiti göz önüne alındığında, yerçekimi sabiti G belirlenebilir. ⓘ
Test kütlelerini sıkıştırarak basınç etkilerini incelemek ümitsizdir, çünkü elde edilebilir laboratuvar basınçları metal bir topun kütle enerjisine kıyasla önemsizdir. ⓘ
Bununla birlikte, protonların atom çekirdekleri içinde sıkıca sıkıştırılmasından kaynaklanan itici elektromanyetik basınçlar tipik olarak 1028 atm ≈ 1033 Pa ≈ 1033 kg-s-2m-1 mertebesindedir. Bu da yaklaşık 1018kg/m3 olan nükleer kütle yoğunluğunun yaklaşık %1'ine denk gelir (c2 ≈ 9×1016m2s-2 hesaba katıldıktan sonra). ⓘ
Eğer basınç yerçekimsel bir kaynak olarak hareket etmiyorsa, o zaman elektrostatik basınçların daha yüksek olduğu daha yüksek atom numarası Z'ye sahip çekirdekler için daha düşük olmalıdır. L. B. Kreuzer (1968), Teflon ile aynı kaldırma yoğunluğuna sahip trikloretilen ve dibromoetan sıvılarının karışımında asılı duran bir Teflon kütlesi kullanarak bir Cavendish deneyi yapmıştır (Şekil 5-9b). Florun atom numarası Z = 9, bromun ise Z = 35'tir. Kreuzer, Teflon kütlesinin yeniden konumlandırılmasının burulma çubuğunda hiçbir farklı sapmaya neden olmadığını, dolayısıyla aktif kütle ile pasif kütlenin 5×10-5 hassasiyetle eşdeğer olduğunu tespit etmiştir. ⓘ
Kreuzer başlangıçta bu deneyi sadece aktif kütlenin pasif kütleye oranının bir testi olarak düşünmüş olsa da, Clifford Will (1976) deneyi kaynakların yerçekimi alanlarına bağlanmasının temel bir testi olarak yeniden yorumladı. ⓘ
1986'da Bartlett ve Van Buren, Ay'ın lazer menzilinin Ay'ın şekil merkezi ile kütle merkezi arasında 2 km'lik bir kayma tespit ettiğini belirtmiştir. Bu, Fe (Ay'ın çekirdeğinde bol miktarda bulunur) ve Al (kabuğunda ve mantosunda bol miktarda bulunur) dağılımında bir asimetri olduğunu gösterir. Eğer basınç uzay-zaman eğriliğine kütle-enerji gibi eşit katkıda bulunmasaydı, Ay klasik mekaniğin öngördüğü yörüngede olmazdı. Ölçümlerini, aktif ve pasif kütle arasındaki herhangi bir tutarsızlığın sınırlarını yaklaşık 10-12'ye kadar sıkılaştırmak için kullandılar. ⓘ
Gravitomanyetizma

Gravitomanyetizmanın varlığı, 20 Nisan 2004 tarihinde fırlatılan uydu tabanlı bir görev olan Gravity Probe B (GP-B) tarafından kanıtlanmıştır. Uzay uçuşu aşaması şu tarihe kadar sürmüştür . Görevin amacı, özellikle yerçekimi manyetizmasına vurgu yaparak Dünya yakınındaki uzay-zaman eğriliğini ölçmekti. ⓘ
İlk sonuçlar nispeten büyük jeodezik etkiyi (basit uzay-zaman eğriliğinden kaynaklanır ve de Sitter presesyonu olarak da bilinir) yaklaşık %1'lik bir doğrulukla teyit etti. Çok daha küçük olan çerçeve sürükleme etkisinin (kütle çekim manyetizmasından kaynaklanır ve Lense-Thirring presesyonu olarak da bilinir) jiroskoplarda değişken kaymaya neden olan beklenmedik yük etkileri nedeniyle ölçülmesi zordu. Bununla birlikte 'de çerçeve sürükleme etkisi beklenen sonucun %15'ine kadar doğrulanırken, jeodezik etki %0,5'ten daha iyi olarak doğrulanmıştır. ⓘ
LARES, LAGEOS-1 ve LAGEOS-2 uydularının lazer menzilli gözlemleriyle yapılan sonraki çerçeve sürükleme ölçümleri, GP-B ölçümünü geliştirdi ve sonuçlar (2016 itibariyle), bu sonucun doğruluğu konusunda bazı anlaşmazlıklar olmasına rağmen, etkinin teorik değerinin %5'i içinde olduğunu gösterdi. ⓘ
Bir başka çalışma olan Gyroscopes in General Relativity (GINGER) deneyi, bu etkiyi ölçmek için Dünya yüzeyinin 1400 m altına birbirine dik açılarla monte edilmiş üç adet 6 m'lik halka lazer kullanmayı amaçlamaktadır. ⓘ
Teknik konular
Uzayzaman gerçekten eğri midir?
Poincaré'nin gelenekselci görüşlerine göre, Öklidyen geometriye karşı Öklidyen olmayan geometriyi seçmek için temel kriterler ekonomi ve basitlik olacaktır. Bir realist Einstein'ın uzay-zamanın Öklid-dışı olduğunu keşfettiğini söyleyecektir. Gelenekselci ise Einstein'ın sadece Öklid-dışı geometriyi kullanmayı daha uygun bulduğunu söyleyecektir. Gelenekselci ise Einstein'ın analizinin uzayzamanın geometrisinin gerçekte ne olduğu hakkında hiçbir şey söylemediğini savunur. ⓘ
Böyle söyleniyor,
- 1. Genel göreliliği düz uzay-zaman açısından temsil etmek mümkün müdür?
- 2. Genel göreliliğin düz uzayzaman yorumunun alışılagelmiş eğri uzayzaman yorumundan daha uygun olabileceği durumlar var mıdır? ⓘ
İlk soruya yanıt olarak, Deser, Grishchuk, Rosen, Weinberg, vb. dahil olmak üzere bir dizi yazar, düz bir manifoldda bir alan olarak yerçekiminin çeşitli formülasyonlarını sağlamıştır. Bu teoriler çeşitli şekillerde "bimetrik kütleçekimi", "genel göreliliğe alan teorik yaklaşım" ve benzeri adlarla anılmaktadır. Kip Thorne bu teorilerin popüler bir incelemesini yapmıştır. ⓘ
Düz uzay-zaman paradigması, maddenin, cetvellerin çevresel yönelimden radyal yöne çevrildiklerinde küçülmelerine ve saatlerin tik tak hızlarının genişlemesine neden olan bir çekim alanı yarattığını öne sürer. Düz uzay-zaman paradigması, her ikisinin de aynı fiziksel olguları temsil etmesi bakımından eğri uzay-zaman paradigmasına tamamen eşdeğerdir. Ancak matematiksel formülasyonları tamamen farklıdır. Çalışan fizikçiler rutin olarak problemin gerekliliklerine bağlı olarak eğri ve düz uzay-zaman tekniklerini kullanmak arasında geçiş yaparlar. Düz uzay-zaman paradigması, zayıf alanlarda yaklaşık hesaplamalar yaparken özellikle kullanışlı olmaktadır. Bu nedenle, kütleçekimsel dalga problemlerini çözerken düz uzayzaman teknikleri kullanılırken, kara deliklerin analizinde eğri uzayzaman teknikleri kullanılacaktır. ⓘ
Asimptotik simetriler
Özel Görelilik için uzay-zaman simetri grubu Poincaré grubudur ve bu grup üç Lorentz güçlendirmesi, üç döndürme ve dört uzay-zaman ötelemesinden oluşan on boyutlu bir gruptur. Genel Görelilikte varsa hangi simetrilerin geçerli olabileceğini sormak mantıklıdır. Çekim alanının tüm kaynaklarından uzakta bulunan gözlemciler tarafından görüldüğü şekliyle uzayzamanın simetrilerini göz önünde bulundurmak izlenebilir bir durum olabilir. Asimptotik olarak düz uzayzaman simetrileri için naif beklenti basitçe özel göreliliğin düz uzayzaman simetrilerini, yani Poincaré grubunu genişletmek ve yeniden üretmek olabilir. ⓘ
1962 yılında Hermann Bondi, M. G. van der Burg, A. W. Metzner ve Rainer K. Sachs, yayılan kütleçekim dalgaları nedeniyle sonsuzdaki enerji akışını araştırmak için bu asimptotik simetri problemini ele aldılar. İlk adımları, bir metriğin asimptotik olarak düz olduğunu söylemenin ne anlama geldiğini karakterize etmek için ışık benzeri sonsuzluktaki yerçekimi alanına yerleştirilecek fiziksel olarak mantıklı bazı sınır koşullarına karar vermekti, asimptotik simetri grubunun doğası hakkında hiçbir önsel varsayımda bulunmadılar - böyle bir grubun var olduğu varsayımı bile. Daha sonra en mantıklı sınır koşulları olarak gördükleri koşulları tasarladıktan sonra, asimptotik olarak düz kütleçekim alanları için uygun sınır koşullarının biçimini değişmez bırakan asimptotik simetri dönüşümlerinin doğasını araştırdılar. Buldukları şey, asimptotik simetri dönüşümlerinin aslında bir grup oluşturduğu ve bu grubun yapısının mevcut olan belirli yerçekimi alanına bağlı olmadığıdır. Bu, beklendiği gibi, uzayzamanın kinematiğinin en azından uzaysal sonsuzlukta kütleçekim alanının dinamiklerinden ayrılabileceği anlamına gelir. 1962'deki şaşırtıcı sürpriz, BMS grubunun bir alt grubu olan sonlu boyutlu Poincaré grubu yerine, asimptotik simetri grubu olarak zengin bir sonsuz boyutlu grubun (BMS grubu olarak adlandırılan) keşfedilmesiydi. Sadece Lorentz dönüşümleri asimptotik simetri dönüşümleri değil, Lorentz dönüşümü olmayan ama asimptotik simetri dönüşümü olan ek dönüşümler de vardır. Aslında, süper dönüşümler olarak bilinen ek bir dönüşüm üreteçleri sonsuzluğu buldular. Bu da Genel Göreliliğin (GR) uzak mesafelerdeki zayıf alanlar söz konusu olduğunda özel göreliliğe indirgenemeyeceği sonucunu ortaya çıkarmaktadır. ⓘ
Eğri manifoldlar
Fiziksel nedenlerden dolayı, uzayzaman sürekliliği matematiksel olarak dört boyutlu, pürüzsüz, bağlantılı Lorentzian manifoldu olarak tanımlanır . Bu, düzgün Lorentz metriği anlamına gelir imzası var . Metrik, uzayzamanın geometrisini belirlediği gibi, parçacıkların ve ışık ışınlarının jeodeziklerini de belirler. Bu manifold üzerindeki her bir nokta (olay) hakkında, referans çerçevelerindeki gözlemcileri temsil etmek için koordinat çizelgeleri kullanılır. Genellikle, Kartezyen koordinatlar kullanılır. Ayrıca, basitlik adına, ölçüm birimleri genellikle ışık hızı 1'e eşittir. ⓘ
Bir referans çerçevesi (gözlemci) bu koordinat şemalarından biriyle tanımlanabilir; böyle bir gözlemci herhangi bir olayı tanımlayabilir . Başka bir referans çerçevesi, aşağıdaki konularda ikinci bir koordinat çizelgesi ile tanımlanabilir . İki gözlemci (her bir referans çerçevesinde bir gözlemci) aynı olayı tanımlayabilir ancak farklı tanımlamalar elde edilir. ⓘ
Bir manifoldu kapsayabilmek için genellikle çok sayıda örtüşen koordinat çizelgesine ihtiyaç duyulur. İki koordinat çizelgesi verildiğinde, biri (bir gözlemciyi temsil eden) ve bir diğerini içeren (başka bir gözlemciyi temsil eden), grafiklerin kesişimi, her iki gözlemcinin de fiziksel nicelikleri ölçebileceği ve dolayısıyla sonuçları karşılaştırabileceği uzay-zaman bölgesini temsil eder. İki ölçüm kümesi arasındaki ilişki, bu kesişim üzerinde tekil olmayan bir koordinat dönüşümü ile verilir. Koordinat çizelgelerinin kendi çevrelerinde ölçüm yapabilen yerel gözlemciler olduğu fikri fiziksel olarak da mantıklıdır, çünkü fiziksel veriler aslında bu şekilde toplanır - yerel olarak. ⓘ
Örneğin, biri Dünya'da, diğeri Jüpiter'e giden hızlı bir rokette bulunan iki gözlemci, Jüpiter'e çarpan bir kuyruklu yıldızı gözlemleyebilir (bu olay ). Genel olarak, bu etkinin tam yeri ve zamanlaması konusunda anlaşmazlığa düşeceklerdir, yani farklı 4'lü çiftlere sahip olacaklardır (farklı koordinat sistemleri kullandıkları için). Kinematik tanımları farklı olsa da, momentum korunumu ve termodinamiğin birinci yasası gibi dinamik (fiziksel) yasalar geçerliliğini koruyacaktır. Aslında görelilik kuramı bundan daha fazlasını gerektirir, çünkü bu (ve diğer tüm fiziksel) yasaların tüm koordinat sistemlerinde aynı biçimi alması gerektiğini şart koşar. Bu, göreliliğe tüm fiziksel niceliklerin temsil edildiği tensörleri sokar. ⓘ
Jeodeziklerin zaman benzeri, boş veya uzay benzeri olduğu söylenir, eğer jeodeziğin bir noktasına teğet vektör bu nitelikteyse. Parçacıkların ve ışık ışınlarının uzayzamandaki yolları sırasıyla zaman benzeri ve boş (ışık benzeri) jeodeziklerle temsil edilir. ⓘ








































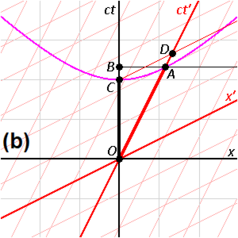

































































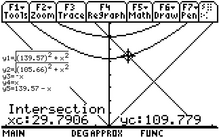





































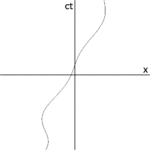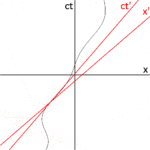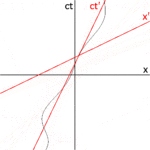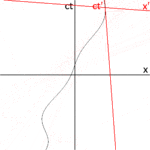









































![{\displaystyle -\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)

![{\displaystyle \left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)





















