Vektör

A'dan B'ye işaret eden bir vektör ⓘ

Matematik, fizik ve mühendislikte, bir Öklid vektörü veya basitçe bir vektör (bazen geometrik vektör veya uzaysal vektör olarak da adlandırılır), büyüklüğü (veya uzunluğu) ve yönü olan geometrik bir nesnedir. Vektörler, vektör cebirine göre diğer vektörlere eklenebilir. Bir Öklid vektörü sıklıkla yönlendirilmiş bir doğru parçası veya grafiksel olarak bir başlangıç noktası A ile bir son nokta B'yi birleştiren bir ok olarak temsil edilir ve şu şekilde gösterilir ${\overrightarrow {AB}}$ . ⓘ

Bir vektör, A noktasını B noktasına "taşımak" için gereken şeydir; Latince vektör kelimesi "taşıyıcı" anlamına gelir. İlk olarak 18. yüzyıl astronomları tarafından Güneş etrafındaki gezegen devrimini araştırırken kullanılmıştır. Vektörün büyüklüğü iki nokta arasındaki mesafeyi, yönü ise A'dan B'ye olan yer değiştirme yönünü ifade eder. Toplama, çıkarma, çarpma ve olumsuzlama gibi gerçek sayılar üzerindeki birçok cebirsel işlemin vektörler için yakın benzerleri vardır; bu işlemler değişebilirlik, birleşebilirlik ve dağılabilirlik gibi bilinen cebirsel yasalara uyar. Bu işlemler ve ilgili yasalar Öklid vektörlerini, basitçe bir vektör uzayının elemanları olarak tanımlanan daha genelleştirilmiş vektör kavramının bir örneği olarak nitelendirir. ⓘ

Vektörler fizikte önemli bir rol oynar: hareket eden bir nesnenin hızı, ivmesi ve üzerine etki eden kuvvetlerin tümü vektörlerle tanımlanabilir. Diğer birçok fiziksel büyüklük de vektörler olarak düşünülebilir. Bunların çoğu mesafeleri temsil etmese de (örneğin konum veya yer değiştirme hariç), büyüklükleri ve yönleri yine de bir okun uzunluğu ve yönü ile temsil edilebilir. Fiziksel bir vektörün matematiksel temsili, onu tanımlamak için kullanılan koordinat sistemine bağlıdır. Fiziksel büyüklükleri tanımlayan ve koordinat sistemindeki değişiklikler altında benzer şekilde dönüşen diğer vektör benzeri nesneler arasında psödovektörler ve tensörler bulunur. ⓘ

Tarihçe

Bugün bildiğimiz şekliyle vektör kavramı, 200 yılı aşkın bir süre boyunca kademeli bir gelişimin sonucudur. Yaklaşık bir düzine insan bu kavramın gelişimine önemli katkılarda bulunmuştur. ⓘ

1835'te Giusto Bellavitis, eşitlik kavramını oluşturduğunda temel fikri soyutlaştırdı. Öklid düzleminde çalışarak, aynı uzunluk ve yönelimdeki herhangi bir paralel doğru parçası çiftini eşdeğer hale getirdi. Esasen, düzlemdeki nokta çiftleri (bipoint) üzerinde bir eşdeğerlik ilişkisi gerçekleştirdi ve böylece düzlemdeki ilk vektör uzayını kurdu. ⓘ

Vektör terimi William Rowan Hamilton tarafından bir kuaterniyonun parçası olarak tanıtılmıştır; bu kuaterniyon q = s + v gerçek sayı s (skaler olarak da adlandırılır) ve 3 boyutlu bir vektörün toplamıdır. Bellavitis gibi Hamilton da vektörleri eşit yönlü segmentlerin sınıflarının temsilcisi olarak görüyordu. Karmaşık sayılar reel doğruyu tamamlamak için hayali bir birim kullandığından, Hamilton v vektörünü bir kuaterniyonun hayali kısmı olarak düşünmüştür:

Geometrik olarak düz bir çizgi ya da yarıçap vektörü tarafından inşa edilen ve genel olarak her belirlenmiş kuaterniyon için uzayda belirlenmiş bir uzunluğa ve belirlenmiş bir yöne sahip olan cebirsel olarak hayali kısım, vektör kısmı ya da basitçe kuaterniyonun vektörü olarak adlandırılabilir. ⓘ

On dokuzuncu yüzyılın ortalarında Augustin Cauchy, Hermann Grassmann, August Möbius, Comte de Saint-Venant ve Matthew O'Brien gibi birçok matematikçi vektör benzeri sistemler geliştirmiştir. Grassmann'ın 1840 tarihli Theorie der Ebbe und Flut (Gelgit ve Akış Teorisi) adlı çalışması, bugünkü sisteme benzer ilk mekânsal analiz sistemiydi ve çapraz çarpım, skaler çarpım ve vektör türevine karşılık gelen fikirlere sahipti. Grassmann'ın çalışmaları 1870'lere kadar büyük ölçüde ihmal edildi. ⓘ

Hamilton'dan sonra kuaterniyon standardını Peter Guthrie Tait taşıdı. Onun 1867 tarihli Elementary Treatise of Quaternions adlı eseri nabla veya del operatörü ∇'nin kapsamlı bir şekilde ele alınmasını içeriyordu. ⓘ

1878 yılında William Kingdon Clifford tarafından Elements of Dynamic yayımlandı. Clifford, iki vektörün nokta çarpımını ve çapraz çarpımını tam kuaterniyon çarpımından izole ederek kuaterniyon çalışmasını basitleştirdi. Bu yaklaşım, vektör hesaplamalarını mühendisler ve üç boyutta çalışan ve dördüncüye şüpheyle yaklaşan diğer kişiler için kullanılabilir hale getirdi. ⓘ

James Clerk Maxwell'in Treatise on Electricity and Magnetism'i aracılığıyla kuaterniyonlara maruz kalan Josiah Willard Gibbs, vektör kısımlarını bağımsız olarak ele almak üzere ayırdı. Gibbs'in 1881'de yayınlanan Elements of Vector Analysis adlı kitabının ilk yarısı, esasen modern vektör analizi sistemini sunmaktadır. 1901'de Edwin Bidwell Wilson, Gibb'in derslerinden uyarladığı Vector Analysis'i yayınladı ve vektör analizinin gelişiminde kuaterniyonlardan söz edilmesini yasakladı. ⓘ

Genel bakış

Fizik ve mühendislikte bir vektör tipik olarak bir büyüklük ve bir yön ile karakterize edilen geometrik bir varlık olarak kabul edilir. Resmi olarak bir Öklid uzayında yönlendirilmiş bir doğru parçası veya ok olarak tanımlanır. Saf matematikte vektör, daha genel olarak bir vektör uzayının herhangi bir elemanı olarak tanımlanır. Bu bağlamda, vektörler bir büyüklük ve bir yön ile karakterize edilebilen ya da edilemeyen soyut varlıklardır. Bu genelleştirilmiş tanım, yukarıda bahsedilen geometrik varlıkların, Öklid uzayı adı verilen özel bir vektör uzayı türünün elemanları oldukları için özel bir vektör türü olduklarını ima eder. ⓘ

Bu makale Öklid uzayında oklar olarak tanımlanan vektörler hakkındadır. Bu özel vektörleri saf matematikte tanımlanan vektörlerden ayırmak gerektiğinde, bazen geometrik, uzaysal veya Öklid vektörleri olarak adlandırılırlar. ⓘ

Bir ok olan Öklid vektörünün belirli bir başlangıç noktası ve son noktası vardır. Başlangıç ve bitiş noktası sabit olan bir vektöre bağlı vektör denir. Vektörün yalnızca büyüklüğü ve yönü önemli olduğunda, belirli bir başlangıç noktasının önemi yoktur ve vektöre serbest vektör denir. Böylece iki ok ${\stackrel {\,\longrightarrow }{AB}}$ ve ${\stackrel {\,\longrightarrow }{A'B'}}$ Uzayda, aynı büyüklük ve yöne sahiplerse aynı serbest vektörü temsil ederler: yani, ABB′A′ dörtgeni bir paralelkenar ise eşdeğerdirler. Eğer Öklid uzayında bir orijin seçimi varsa, o zaman serbest vektör, başlangıç noktası orijin olan aynı büyüklük ve yöndeki bağlı vektöre eşdeğerdir. ⓘ

Vektör teriminin ayrıca daha yüksek boyutlara ve çok daha geniş uygulamaları olan daha resmi yaklaşımlara genellemeleri vardır. ⓘ

Daha fazla bilgi

Klasik Öklid geometrisinde (yani sentetik geometride), vektörler (19. yüzyılda) sıralı nokta çiftlerinin eşdeğerlik altında denklik sınıfları olarak tanıtılmıştır; iki çift (A, B) ve (C, D), bu sırayla A, B, D, C noktaları bir paralelkenar oluşturuyorsa eşdeğerdir. Böyle bir denklik sınıfına vektör, daha doğrusu Öklid vektörü denir. (A, B)'nin eşdeğerlik sınıfı genellikle şu şekilde gösterilir ${\overrightarrow {AB}}.$ ⓘ

Dolayısıyla bir Öklid vektörü, aynı büyüklüğe (örneğin, (A, B) doğru parçasının uzunluğu) ve aynı yöne (örneğin, A'dan B'ye olan yön) sahip yönlendirilmiş parçaların bir eşdeğerlik sınıfıdır. Fizikte Öklid vektörleri, yönü olmayan skalerlerin aksine, hem büyüklüğü hem de yönü olan ancak belirli bir yerde bulunmayan fiziksel büyüklükleri temsil etmek için kullanılır. Örneğin, hız, kuvvetler ve ivme vektörlerle temsil edilir. ⓘ

Modern geometride Öklid uzayları genellikle lineer cebirden tanımlanır. Daha açık bir ifadeyle, bir E Öklid uzayı, gerçekler üzerinde sonlu boyutlu bir iç çarpım uzayının ilişkilendirildiği bir küme olarak tanımlanır ${\overrightarrow {E}},$ 'nin toplamsal grubunun bir grup eylemidir. ${\overrightarrow {E}},$ serbest ve geçişlidir (Bu yapının ayrıntıları için bkz. afin uzay). Elemanları ${\overrightarrow {E}}$ öteleme olarak adlandırılır. ⓘ

Öklid uzaylarının iki tanımının eşdeğer olduğu ve eşdeğerlik altındaki denklik sınıflarının ötelemelerle tanımlanabileceği kanıtlanmıştır. ⓘ

Bazen, Öklid vektörleri bir Öklid uzayına atıfta bulunulmadan ele alınır. Bu durumda, bir Öklid vektörü, gerçekler üzerinde sonlu boyutlu normlu bir vektör uzayının bir elemanıdır veya tipik olarak $\mathbb {R} ^{n}$ nokta çarpımı ile donatılmıştır. Bu mantıklıdır, çünkü böyle bir vektör uzayında toplama işlemi vektör uzayının kendisi üzerinde serbestçe ve geçişli olarak etki eder. Yani, $\mathbb {R} ^{n}$ bir Öklid uzayıdır, kendisi ilişkili bir vektör uzayıdır ve nokta çarpımı bir iç çarpımdır. ⓘ

Öklid uzayı $\mathbb {R} ^{n}$ Bu, n boyutlu her Öklid uzayının Öklid uzayına izomorfik olduğu gerçeğiyle motive edilir. $\mathbb {R} ^{n}.$ Daha doğrusu, böyle bir Öklid uzayı verildiğinde, herhangi bir O noktası orijin olarak seçilebilir. Gram-Schmidt işlemiyle, ilgili vektör uzayının ortonormal bir temeli de bulunabilir (öyle bir temel ki, iki temel vektörün iç çarpımı farklıysa 0, eşitse 1 olsun). Bu, uzayın herhangi bir P noktasının kartezyen koordinatlarını, vektörün bu temeli üzerindeki koordinatlar olarak tanımlar ${\overrightarrow {OP}}.$ Bu seçimler, verilen Öklid uzayının bir izomorfizmini tanımlar $\mathbb {R} ^{n},$ Herhangi bir noktayı Kartezyen koordinatlarının n-tuple'ına ve her vektörü koordinat vektörüne eşleyerek. ⓘ

Tek boyutta örnekler

Fizikçinin kuvvet kavramı bir yöne ve bir büyüklüğe sahip olduğundan, bir vektör olarak görülebilir. Örnek olarak, sağa doğru 15 newtonluk bir F kuvveti düşünün. Eğer pozitif eksen de sağa doğruysa, F 15 N vektörü ile temsil edilir ve eğer pozitif sola doğruysa, F vektörü -15 N olur. Her iki durumda da, vektörün büyüklüğü 15 N'dir. Benzer şekilde, 4 metrelik bir Δs yer değiştirmesinin vektör gösterimi, yönüne bağlı olarak 4 m veya -4 m olacaktır ve büyüklüğü ne olursa olsun 4 m olacaktır. ⓘ

Fizik ve mühendislikte

Vektörler fiziksel bilimlerin temelini oluşturur. Büyüklüğü olan, yönü olan ve vektör toplama kurallarına uyan herhangi bir miktarı temsil etmek için kullanılabilirler. Buna bir örnek, büyüklüğü hız olan hızdır. Örneğin, saniyede 5 metre yukarı doğru olan hız (0, 5) vektörü ile temsil edilebilir (2 boyutta pozitif y ekseni 'yukarı' olacak şekilde). Bir vektör tarafından temsil edilen bir başka nicelik de kuvvettir, çünkü bir büyüklüğü ve yönü vardır ve vektör toplama kurallarına uyar. Vektörler ayrıca doğrusal yer değiştirme, yer değiştirme, doğrusal ivme, açısal ivme, doğrusal momentum ve açısal momentum gibi diğer birçok fiziksel niceliği de tanımlar. Elektrik ve manyetik alan gibi diğer fiziksel vektörler, fiziksel bir uzayın her noktasında bir vektör sistemi olarak temsil edilir; yani bir vektör alanı. Büyüklüğü ve yönü olan ancak vektör toplama kurallarına uymayan büyüklüklere örnek olarak açısal yer değiştirme ve elektrik akımı verilebilir. Sonuç olarak bunlar vektör değildir. ⓘ

Kartezyen uzayda

Kartezyen koordinat sisteminde, bir sınır vektörü başlangıç ve bitiş noktalarının koordinatları belirlenerek temsil edilebilir. Örneğin, uzaydaki A = (1, 0, 0) ve B = (0, 1, 0) noktaları sınır vektörünü belirler ${\overrightarrow {AB}}$ x ekseni üzerindeki x = 1 noktasından y ekseni üzerindeki y = 1 noktasına işaret eder. ⓘ

Kartezyen koordinatlarda, bir serbest vektör, bu anlamda, başlangıç noktası O = (0, 0, 0) orijin koordinatlarına sahip olan karşılık gelen bir bağlı vektör açısından düşünülebilir. Daha sonra bu bağlı vektörün terminal noktasının koordinatları tarafından belirlenir. Böylece (1, 0, 0) ile temsil edilen serbest vektör, pozitif x ekseni yönünde işaret eden birim uzunlukta bir vektördür. ⓘ

Serbest vektörlerin bu koordinat gösterimi, cebirsel özelliklerinin uygun bir sayısal şekilde ifade edilmesini sağlar. Örneğin, iki (serbest) vektörün (1, 2, 3) ve (-2, 0, 4) toplamı (serbest) vektördür

$$(1,2,3)+(-2,0,4)=(1-2,2+0,3+4)=(-1,2,7)\,.$$

ⓘ

Öklid ve afin vektörler

Geometrik ve fiziksel ortamlarda, bazen vektörlere doğal bir şekilde bir uzunluk veya büyüklük ve bir yön atfetmek mümkündür. Buna ek olarak, yön kavramı iki vektör arasındaki açı kavramı ile sıkı bir şekilde ilişkilidir. Eğer iki vektörün nokta çarpımı tanımlanırsa -iki vektörün skaler değerli çarpımı- o zaman bir uzunluk tanımlamak da mümkündür; nokta çarpımı hem açı (sıfır olmayan herhangi iki vektör arasındaki nokta çarpımının bir fonksiyonu) hem de uzunluk (bir vektörün kendisiyle nokta çarpımının karekökü) için uygun bir cebirsel karakterizasyon sağlar. Üç boyutta, iki vektör tarafından tanımlanan (paralelkenarın kenarları olarak kullanılan) paralelkenarın uzaydaki alanının ve yönünün cebirsel bir tanımlamasını sağlayan çapraz çarpımı tanımlamak da mümkündür. Herhangi bir boyutta (ve özellikle daha yüksek boyutlarda), (diğer şeylerin yanı sıra) n vektör tarafından tanımlanan n boyutlu paralelotopun uzaydaki alanının ve yönünün cebirsel bir karakterizasyonunu sağlayan dış çarpımı tanımlamak mümkündür. ⓘ

Bir sözde Öklid uzayında, bir vektörün karesel uzunluğu pozitif, negatif veya sıfır olabilir. Önemli bir örnek Minkowski uzayıdır (özel görelilik anlayışımız için önemlidir). ⓘ

Bununla birlikte, bir vektörün uzunluğunu tanımlamak her zaman mümkün veya arzu edilir değildir. Bu daha genel uzamsal vektör türü, vektör uzaylarının (serbest vektörler için) ve afin uzaylarının (her biri sıralı bir "nokta" çifti ile temsil edilen bağlı vektörler için) konusudur. Fiziksel bir örnek termodinamikten gelir; burada ilgilenilen birçok nicelik, uzunluk veya açı kavramı olmayan bir uzayda vektörler olarak düşünülebilir. ⓘ

Genelleştirmeler

Fizikte olduğu kadar matematikte de bir vektör genellikle bir dizi temel vektör için skaler katsayılar olarak hareket eden bir dizi bileşen veya sayı listesi ile tanımlanır. Temel, örneğin döndürme veya germe yoluyla dönüştürüldüğünde, bu temel açısından herhangi bir vektörün bileşenleri de ters anlamda dönüşür. Vektörün kendisi değişmemiştir, ancak temel değişmiştir, bu nedenle vektörün bileşenleri telafi etmek için değişmelidir. Vektörün bileşenlerinin dönüşümünün temelin dönüşümü ile nasıl ilişkili olduğuna bağlı olarak vektör kovaryant veya kontravaryant olarak adlandırılır. Genel olarak, kontravaryant vektörler mesafe (yer değiştirme gibi) veya mesafe çarpı başka bir birim (hız veya ivme gibi) birimlerine sahip "düzenli vektörlerdir"; diğer yandan, kovaryant vektörler gradyan gibi bir-üstü-mesafe birimlerine sahiptir. Birimleri (temel değişikliğinin özel bir durumu) metreden milimetreye değiştirirseniz, 1/1000'lik bir ölçek faktörü, 1 m'lik bir yer değiştirme 1000 mm olur - sayısal değerde kontravaryant bir değişiklik. Buna karşılık, 1 K/m'lik bir gradyan 0,001 K/mm'ye dönüşür; bu da değerde kovaryant bir değişimdir (daha fazlası için vektörlerin kovaryans ve kontrvaryansına bakınız). Tensörler bu şekilde davranan bir başka nicelik türüdür; bir vektör tensörün bir türüdür. ⓘ

Saf matematikte vektör, bir alan üzerindeki vektör uzayının herhangi bir elemanıdır ve genellikle bir koordinat vektörü olarak gösterilir. Bu makalede tanımlanan vektörler bu genel tanımın çok özel bir durumudur, çünkü ortam uzayına göre kontravaryanttırlar. Kontravaryans, bir vektörün "büyüklüğü ve yönü" olduğu fikrinin arkasındaki fiziksel sezgiyi yakalar. ⓘ

Temsiller

Vektörler genellikle küçük kalın harflerle gösterilir, örneğin $\mathbf {u}$, $\mathbf {v}$ ve $\mathbf {w}$veya a'da olduğu gibi küçük italik kalın harflerle (Büyük harfler genellikle matrisleri temsil etmek için kullanılır.) Diğer kurallar şunlardır ${\vec {a}}$ veya a, özellikle el yazısında. Alternatif olarak, bazıları bir tilde (~) veya sembolün altına çizilen dalgalı bir alt çizgi kullanır, örn. ${\underset {^{\sim }}{a}}$Bu, kalın yazı tipini belirtmek için kullanılan bir kuraldır. Vektör, bir A noktasından bir B noktasına doğru yönlendirilmiş bir mesafeyi veya yer değiştirmeyi temsil ediyorsa (şekle bakın), şu şekilde de gösterilebilir ${\stackrel {\longrightarrow }{AB}}$ ya da AB. Alman edebiyatında, vektörleri küçük fraktur harfleriyle temsil etmek özellikle yaygındı, örneğin ${\mathfrak {a}}$. ⓘ

Vektörler genellikle grafiklerde veya diğer diyagramlarda şekilde gösterildiği gibi oklar (yönlendirilmiş doğru parçaları) olarak gösterilir. Burada A noktası orijin, kuyruk, taban veya başlangıç noktası, B noktası ise baş, uç, bitiş noktası, terminal noktası veya son nokta olarak adlandırılır. Okun uzunluğu vektörün büyüklüğü ile orantılıdır, okun gösterdiği yön ise vektörün yönünü gösterir. ⓘ

İki boyutlu bir diyagramda, bazen diyagramın düzlemine dik bir vektör istenir. Bu vektörler genellikle küçük daireler olarak gösterilir. Merkezinde nokta bulunan bir daire (Unicode U+2299 ⊙) diyagramın ön tarafından izleyiciye doğru bakan bir vektörü gösterir. İçinde çarpı işareti bulunan bir daire (Unicode U+2297 ⊗), diyagramın içine ve arkasına işaret eden bir vektörü gösterir. Bunlar, bir okun başının ucunu görmek ve bir okun uçuşlarını arkadan görmek olarak düşünülebilir. ⓘ

Kartezyen düzlemde, koordinatları (2, 3) olan bir A noktasının konumunu gösteren bir vektör. ⓘ

Vektörlerle hesaplama yapmak için grafiksel gösterim çok hantal olabilir. N-boyutlu Öklid uzayında vektörler, Kartezyen koordinat sisteminde koordinat vektörleri olarak gösterilebilir. Bir vektörün uç noktası n gerçek sayıdan oluşan sıralı bir liste (n-tuple) ile tanımlanabilir. Bu sayılar, belirli bir Kartezyen koordinat sistemine göre vektörün uç noktasının koordinatlarıdır ve tipik olarak vektörün koordinat sisteminin eksenleri üzerindeki skaler bileşenleri (veya skaler izdüşümleri) olarak adlandırılır. ⓘ

İki boyutta bir örnek olarak (şekle bakın), O = (0, 0) orijininden A = (2, 3) noktasına giden vektör basitçe şöyle yazılır

$$\mathbf {a} =(2,3).$$

ⓘ

Vektörün kuyruğunun orijin ile çakıştığı kavramı örtüktür ve kolayca anlaşılabilir. Bu nedenle, daha açık gösterim ${\overrightarrow {OA}}$ genellikle gerekli görülmez (ve gerçekten de nadiren kullanılır). ⓘ

Üç boyutlu Öklid uzayında (veya R³), vektörler skaler bileşenlerin üçlüleri ile tanımlanır:

$$\mathbf {a} =(a_{1},a_{2},a_{3}).$$

ayrıca yazılır,

$$\mathbf {a} =(a_{x},a_{y},a_{z}).$$

ⓘ

Bu, n boyutlu Öklid uzayına (veya Rn) genelleştirilebilir.

$$\mathbf {a} =(a_{1},a_{2},a_{3},\cdots ,a_{n-1},a_{n}).$$

ⓘ

Bu sayılar, özellikle matrislerle uğraşırken, genellikle aşağıdaki gibi bir sütun vektörü veya satır vektörü olarak düzenlenir:

$$\mathbf {a} ={\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\\\end{bmatrix}}=[a_{1}\ a_{2}\ a_{3}]^{\operatorname {T} }.$$

ⓘ

Bir vektörü n-boyutta temsil etmenin bir başka yolu da standart temel vektörleri tanıtmaktır. Örneğin, üç boyutta bunlardan üç tane vardır:

$${\mathbf {e} }_{1}=(1,0,0),\ {\mathbf {e} }_{2}=(0,1,0),\ {\mathbf {e} }_{3}=(0,0,1).$$

Bunlar sezgisel olarak sırasıyla Kartezyen koordinat sisteminin x-, y- ve z-eksenlerini işaret eden birim uzunluktaki vektörler olarak yorumlanır. Bunlar açısından, R³'teki herhangi bir a vektörü şu şekilde ifade edilebilir:

$$\mathbf {a} =(a_{1},a_{2},a_{3})=a_{1}(1,0,0)+a_{2}(0,1,0)+a_{3}(0,0,1),\$$

ⓘ

veya

$$\mathbf {a} =\mathbf {a} _{1}+\mathbf {a} _{2}+\mathbf {a} _{3}=a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2}+a_{3}{\mathbf {e} }_{3},$$

ⓘ

Burada a₁, a₂, a₃, a'nın temel vektörler üzerindeki vektör bileşenleri (veya vektör izdüşümleri) veya eşdeğer olarak, karşılık gelen x, y ve z Kartezyen eksenleri (şekle bakın) olarak adlandırılırken, a₁, a₂, a₃ ilgili skaler bileşenlerdir (veya skaler izdüşümler). ⓘ

Fiziğe giriş ders kitaplarında, standart temel vektörler genellikle şu şekilde gösterilir $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ yerine (veya $\mathbf {\hat {x}} ,\mathbf {\hat {y}} ,\mathbf {\hat {z}}$burada şapka sembolü ^ tipik olarak birim vektörleri belirtir). Bu durumda, skaler ve vektör bileşenleri sırasıyla a_x, ay, az ve a_x, ay, az olarak gösterilir (kalın harflerle yazılmış farka dikkat edin). Böylece, ⓘ

$$\mathbf {a} =\mathbf {a} _{x}+\mathbf {a} _{y}+\mathbf {a} _{z}=a_{x}{\mathbf {i} }+a_{y}{\mathbf {j} }+a_{z}{\mathbf {k} }.$$

ⓘ

ei gösterimi, yüksek seviyeli matematik, fizik ve mühendislikte yaygın olarak kullanılan indeks gösterimi ve toplama kuralıyla uyumludur. ⓘ

Ayrıştırma veya çözümleme

Yukarıda açıklandığı gibi, bir vektör genellikle verilen vektörü oluşturmak için toplanan bir dizi vektör bileşeni ile tanımlanır. Tipik olarak, bu bileşenler vektörün bir dizi karşılıklı dik referans ekseni (temel vektörler) üzerindeki izdüşümleridir. Vektörün bu kümeye göre ayrıştırıldığı veya çözüldüğü söylenir. ⓘ

Bir vektörün bir yüzeye teğetsel ve normal bileşenlerinin gösterimi. ⓘ

Bir vektörün bileşenlerine ayrıştırılması veya çözümlenmesi benzersiz değildir, çünkü vektörün yansıtıldığı eksenlerin seçimine bağlıdır. ⓘ

Ayrıca, aşağıdaki gibi Kartezyen birim vektörlerin kullanımı $\mathbf {\hat {x}} ,\mathbf {\hat {y}} ,\mathbf {\hat {z}}$ bir vektörün temsil edileceği bir temel olarak zorunlu değildir. Vektörler, silindirik bir koordinat sisteminin birim vektörleri de dahil olmak üzere keyfi bir temel cinsinden de ifade edilebilir (${\boldsymbol {\hat {\rho }}},{\boldsymbol {\hat {\phi }}},\mathbf {\hat {z}}$) veya küresel koordinat sistemi ($\mathbf {\hat {r}} ,{\boldsymbol {\hat {\theta }}},{\boldsymbol {\hat {\phi }}}$). Son iki seçenek, sırasıyla silindirik veya küresel simetriye sahip problemleri çözmek için daha uygundur. ⓘ

Temel seçimi bir vektörün özelliklerini veya dönüşümler altındaki davranışını etkilemez. ⓘ

Bir vektör, zamanın veya uzayın bir fonksiyonu olarak yönelimlerini değiştiren "sabit olmayan" temel vektörlere göre de parçalanabilir. Örneğin, üç boyutlu uzaydaki bir vektör, sırasıyla normal ve bir yüzeye teğet olmak üzere iki eksene göre ayrıştırılabilir (şekle bakın). Dahası, bir vektörün radyal ve teğetsel bileşenleri bir nesnenin dönme yarıçapı ile ilgilidir. Birincisi yarıçapa paralel, ikincisi ise yarıçapa ortogonaldir. ⓘ

Bu durumlarda, bileşenlerin her biri sabit bir koordinat sistemine veya temel kümesine (örneğin, küresel bir koordinat sistemi veya eylemsiz referans çerçevesi) göre ayrıştırılabilir. ⓘ

Temel özellikler

Aşağıdaki bölümde temel vektörleri olan Kartezyen koordinat sistemi kullanılmaktadır

$${\mathbf {e} }_{1}=(1,0,0),\ {\mathbf {e} }_{2}=(0,1,0),\ {\mathbf {e} }_{3}=(0,0,1)$$

ve tüm vektörlerin ortak bir temel nokta olarak orijine sahip olduğunu varsayar. Bir a vektörü şu şekilde yazılacaktır

$${\mathbf {a} }=a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2}+a_{3}{\mathbf {e} }_{3}.$$

ⓘ

Eşitlik

İki vektörün aynı büyüklük ve yöne sahip olmaları durumunda eşit oldukları söylenir. Eşdeğer olarak, koordinatları eşitse eşit olacaklardır. Yani iki vektör

$${\mathbf {a} }=a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2}+a_{3}{\mathbf {e} }_{3}$$

ve

$${\mathbf {b} }=b_{1}{\mathbf {e} }_{1}+b_{2}{\mathbf {e} }_{2}+b_{3}{\mathbf {e} }_{3}$$

eğer eşitse

$$a_{1}=b_{1},\quad a_{2}=b_{2},\quad a_{3}=b_{3}.\,$$

ⓘ

Zıt, paralel ve antiparalel vektörler

İki vektör aynı büyüklüğe ancak zıt yöne sahipse zıttır. Yani iki vektör

$${\mathbf {a} }=a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2}+a_{3}{\mathbf {e} }_{3}$$

ve

$${\mathbf {b} }=b_{1}{\mathbf {e} }_{1}+b_{2}{\mathbf {e} }_{2}+b_{3}{\mathbf {e} }_{3}$$

ise zıttır

$$a_{1}=-b_{1},\quad a_{2}=-b_{2},\quad a_{3}=-b_{3}.\,$$

İki vektör aynı yöne sahip ancak aynı büyüklükte olmaları gerekmiyorsa paraleldir veya zıt yöne sahip ancak aynı büyüklükte olmaları gerekmiyorsa antiparaleldir. ⓘ

Toplama ve çıkarma

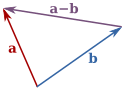
Şimdi a ve b'nin eşit vektörler olması gerekmediğini, ancak farklı büyüklük ve yönlere sahip olabileceklerini varsayalım. a ve b'nin toplamı

$$\mathbf {a} +\mathbf {b} =(a_{1}+b_{1})\mathbf {e} _{1}+(a_{2}+b_{2})\mathbf {e} _{2}+(a_{3}+b_{3})\mathbf {e} _{3}.$$

ⓘ

Toplama işlemi, b okunun kuyruğunu a okunun başına yerleştirerek ve ardından a'nın kuyruğundan b'nin başına bir ok çizerek grafiksel olarak gösterilebilir. Çizilen yeni ok, aşağıda gösterildiği gibi a + b vektörünü temsil eder:

Bu toplama yöntemi bazen paralelkenar kuralı olarak adlandırılır çünkü a ve b bir paralelkenarın kenarlarını oluşturur ve a + b köşegenlerden biridir. Eğer a ve b aynı taban noktasına sahip bağlı vektörlerse, bu nokta aynı zamanda a + b'nin de taban noktası olacaktır. a + b = b + a ve (a + b) + c = a + (b + c) olduğu geometrik olarak kontrol edilebilir. ⓘ

a ve b'nin farkı ⓘ

$$\mathbf {a} -\mathbf {b} =(a_{1}-b_{1})\mathbf {e} _{1}+(a_{2}-b_{2})\mathbf {e} _{2}+(a_{3}-b_{3})\mathbf {e} _{3}.$$

ⓘ

İki vektörün çıkarılması geometrik olarak şu şekilde gösterilebilir: a'dan b'yi çıkarmak için, a ve b'nin kuyruklarını aynı noktaya yerleştirin ve ardından b'nin başından a'nın başına bir ok çizin. Bu yeni ok (-b) + a vektörünü temsil eder, (-b) b'nin tersidir, çizime bakın. Ve (-b) + a = a - b. ⓘ

Skaler çarpma

Bir vektörün 3 faktörü ile skaler çarpımı vektörü uzatır. ⓘ

Bir vektör ayrıca bir r reel sayısı ile çarpılabilir veya yeniden ölçeklendirilebilir. Geleneksel vektör cebiri bağlamında, bu reel sayılar vektörlerden ayırt etmek için genellikle skaler (ölçekten) olarak adlandırılır. Bir vektörü bir skaler ile çarpma işlemine skaler çarpma denir. Elde edilen vektör ⓘ

$$r\mathbf {a} =(ra_{1})\mathbf {e} _{1}+(ra_{2})\mathbf {e} _{2}+(ra_{3})\mathbf {e} _{3}.$$

ⓘ

Sezgisel olarak, bir skaler r ile çarpmak bir vektörü r katsayısı kadar uzatır. Geometrik olarak bu, (en azından r bir tam sayı olduğunda) vektörün r kopyasını, bir vektörün bitiş noktasının bir sonraki vektörün başlangıç noktası olduğu bir çizgiye yerleştirmek olarak görselleştirilebilir. ⓘ

Eğer r negatifse, vektör yön değiştirir: 180°'lik bir açıyla döner. İki örnek (r = -1 ve r = 2) aşağıda verilmiştir:

Bir a vektörünün -a ve 2a skaler çarpımları ⓘ

Skaler çarpma, aşağıdaki anlamda vektör toplama üzerinde dağıtıcıdır: r(a + b) = ra + rb tüm a ve b vektörleri ve tüm r skalerleri için. a - b = a + (-1)b olduğu da gösterilebilir. ⓘ

• Sayıl ile birleşme: $r(s\mathbf {a} )=(rs)\mathbf {a}$
• Sayıl toplaması üzerine dağılma: $(r+s)\mathbf {a} =r\mathbf {a} +s\mathbf {a}$
• Vektör toplamı üzerine dağılma: $r(\mathbf {a} +\mathbf {b} )=r\mathbf {a} +r\mathbf {b}$
• Sayıl birim öğe ile çarpma: $1\mathbf {a} =\mathbf {a}$ ⓘ

özellikleri sağlanır. ⓘ

$r\mathbf {a} ={\begin{bmatrix}ra_{1}&ra_{2}&\cdots &ra_{n}\end{bmatrix}}$ ⓘ

Uzunluk

a vektörünün uzunluğu veya büyüklüğü veya normu ‖a‖ veya daha az yaygın olarak |a| ile gösterilir ve mutlak değerle (skaler bir "norm") karıştırılmamalıdır. ⓘ

a vektörünün uzunluğu Öklid normu ile hesaplanabilir, ⓘ

$$\left\|\mathbf {a} \right\|={\sqrt {a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}},$$

ⓘ

Bu da Pisagor teoreminin bir sonucudur, çünkü e₁, e₂, e₃ temel vektörleri ortogonal birim vektörlerdir. ⓘ

Bu, aşağıda tartışılan, vektörün kendisiyle nokta çarpımının kareköküne eşit olur:

$$\left\|\mathbf {a} \right\|={\sqrt {\mathbf {a} \cdot \mathbf {a} }}.$$

ⓘ

Birim vektör

Bir a vektörünün bir birim vektöre normalleştirilmesi ⓘ

Birim vektör, uzunluğu bir olan herhangi bir vektördür; normalde birim vektörler sadece yön belirtmek için kullanılır. Rastgele uzunluktaki bir vektör, birim vektör oluşturmak için uzunluğuna bölünebilir. Bu, bir vektörün normalleştirilmesi olarak bilinir. Birim vektör genellikle â'da olduğu gibi bir şapka ile gösterilir. ⓘ

Bir a = (a₁, a₂, a₃) vektörünü normalleştirmek için, vektörü uzunluğunun tersi olan ‖a‖ ile ölçeklendirin. Yani:

$$\mathbf {\hat {a}} ={\frac {\mathbf {a} }{\left\|\mathbf {a} \right\|}}={\frac {a_{1}}{\left\|\mathbf {a} \right\|}}\mathbf {e} _{1}+{\frac {a_{2}}{\left\|\mathbf {a} \right\|}}\mathbf {e} _{2}+{\frac {a_{3}}{\left\|\mathbf {a} \right\|}}\mathbf {e} _{3}$$

ⓘ

Sıfır vektör

Sıfır vektörü, uzunluğu sıfır olan vektördür. Koordinatlarla yazıldığında vektör (0, 0, 0) olur ve genellikle şu şekilde gösterilir ${\vec {0}}$Diğer vektörlerden farklı olarak, keyfi ya da belirsiz bir yöne sahiptir ve normalleştirilemez (yani, sıfır vektörünün katı olan bir birim vektör yoktur). Sıfır vektörünün herhangi bir a vektörü ile toplamı a'dır (yani, 0 + a = a). ⓘ

Nokta çarpımı

İki a ve b vektörünün nokta çarpımı (bazen iç çarpım veya sonucu bir skaler olduğu için skaler çarpım olarak da adlandırılır) a ∙ b ile gösterilir ve şu şekilde tanımlanır:

$$\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta ,$$

ⓘ

Burada θ, a ve b arasındaki açının ölçüsüdür (kosinüsün açıklaması için trigonometrik fonksiyona bakınız). Geometrik olarak bu, a ve b'nin ortak bir başlangıç noktasıyla çizildiği ve ardından a'nın uzunluğunun b'nin a ile aynı yönü gösteren bileşeninin uzunluğuyla çarpıldığı anlamına gelir. ⓘ

Nokta çarpım, her bir vektörün bileşenlerinin çarpımlarının toplamı olarak da tanımlanabilir ⓘ

$$\mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}.$$

ⓘ

Çapraz ürün

Çapraz çarpım (vektör çarpımı veya dış çarpım olarak da adlandırılır) yalnızca üç veya yedi boyutta anlamlıdır. Çapraz çarpımın nokta çarpımdan farkı, iki vektörün çapraz çarpımının sonucunun bir vektör olmasıdır. Çapraz çarpım, a × b olarak gösterilir, hem a hem de b'ye dik bir vektördür ve şu şekilde tanımlanır ⓘ

$$\mathbf {a} \times \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\sin(\theta )\,\mathbf {n}$$

ⓘ

Burada θ, a ve b arasındaki açının ölçüsüdür ve n, sağ-elli bir sistemi tamamlayan hem a hem de b'ye dik bir birim vektördür. Sağ-elli olma kısıtlaması gereklidir çünkü hem a hem de b'ye dik olan iki birim vektör vardır, yani n ve (-n). ⓘ

Çapraz çarpımın bir örneği ⓘ

a × b çapraz çarpımı, a, b ve a × b'nin de sağ-elli bir sistem olması için tanımlanır (a ve b'nin ortogonal olması gerekmese de). Bu sağ el kuralıdır. ⓘ

a × b uzunluğu, kenarları a ve b olan paralelkenarın alanı olarak yorumlanabilir. ⓘ

Çapraz çarpım şu şekilde yazılabilir

$${\mathbf {a} }\times {\mathbf {b} }=(a_{2}b_{3}-a_{3}b_{2}){\mathbf {e} }_{1}+(a_{3}b_{1}-a_{1}b_{3}){\mathbf {e} }_{2}+(a_{1}b_{2}-a_{2}b_{1}){\mathbf {e} }_{3}.$$

ⓘ

Uzaysal yönelimin keyfi seçimleri için (yani, sol elin yanı sıra sağ el koordinat sistemlerine de izin vererek) iki vektörün çapraz çarpımı bir vektör yerine bir sözde vektördür (aşağıya bakınız). ⓘ

Skaler üçlü çarpım

Skaler üçlü çarpım (kutu çarpımı veya karışık üçlü çarpım olarak da adlandırılır) aslında yeni bir operatör değildir, ancak diğer iki çarpma operatörünü üç vektöre uygulamanın bir yoludur. Skaler üçlü çarpım bazen (a b c) ile gösterilir ve şu şekilde tanımlanır:

$$(\mathbf {a} \ \mathbf {b} \ \mathbf {c} )=\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ).$$

ⓘ

Üç temel kullanımı vardır. Birincisi, kutu çarpımının mutlak değeri, üç vektör tarafından tanımlanan kenarları olan paralel yüzlü bir cismin hacmidir. İkincisi, skaler üçlü çarpım, ancak ve ancak üç vektör doğrusal olarak bağımlıysa sıfırdır; bu, üç vektörün bir hacim oluşturmaması için hepsinin aynı düzlemde olması gerektiği düşünülerek kolayca kanıtlanabilir. Üçüncü olarak, kutu çarpımı ancak ve ancak üç vektör a, b ve c sağ elli ise pozitiftir. ⓘ

Bileşenlerde (sağ elli bir ortonormal temele göre), üç vektör satır (veya sütun, ancak aynı sırada) olarak düşünülürse, skaler üçlü çarpım basitçe üç vektörü satır olarak içeren 3'e 3 matrisin determinantıdır

$$(\mathbf {a} \ \mathbf {b} \ \mathbf {c} )={\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\\\end{vmatrix}}$$

ⓘ

Skaler üçlü çarpım her üç girişte de doğrusaldır ve aşağıdaki anlamda anti-simetriktir:

$$(\mathbf {a} \ \mathbf {b} \ \mathbf {c} )=(\mathbf {c} \ \mathbf {a} \ \mathbf {b} )=(\mathbf {b} \ \mathbf {c} \ \mathbf {a} )=-(\mathbf {a} \ \mathbf {c} \ \mathbf {b} )=-(\mathbf {b} \ \mathbf {a} \ \mathbf {c} )=-(\mathbf {c} \ \mathbf {b} \ \mathbf {a} ).$$

ⓘ

Çoklu Kartezyen tabanlar arasında dönüşüm

Şimdiye kadarki tüm örnekler, aynı taban cinsinden ifade edilen vektörlerle, yani e tabanı {e₁, e₂, e₃} ile ilgiliydi. Ancak, bir vektör, birbiriyle aynı hizada olması gerekmeyen herhangi bir sayıda farklı taban cinsinden ifade edilebilir ve yine de aynı vektör olarak kalır. e tabanında, bir a vektörü tanım gereği şu şekilde ifade edilir ⓘ

$$\mathbf {a} =p\mathbf {e} _{1}+q\mathbf {e} _{2}+r\mathbf {e} _{3}.$$

ⓘ

e temelindeki skaler bileşenler tanım gereği şunlardır, ⓘ

$${\begin{aligned}p&=\mathbf {a} \cdot \mathbf {e} _{1},\\q&=\mathbf {a} \cdot \mathbf {e} _{2},\\r&=\mathbf {a} \cdot \mathbf {e} _{3}.\end{aligned}}$$

ⓘ

e ile aynı hizada olması gerekmeyen n = {n₁, n₂, n₃} başka bir ortonormal temelde a vektörü şu şekilde ifade edilir ⓘ

$$\mathbf {a} =u\mathbf {n} _{1}+v\mathbf {n} _{2}+w\mathbf {n} _{3}$$

ⓘ

ve n temelindeki skaler bileşenler tanım gereği şunlardır, ⓘ

$${\begin{aligned}u&=\mathbf {a} \cdot \mathbf {n} _{1},\\v&=\mathbf {a} \cdot \mathbf {n} _{2},\\w&=\mathbf {a} \cdot \mathbf {n} _{3}.\end{aligned}}$$

ⓘ

p, q, r ve u, v, w değerleri birim vektörlerle öyle bir şekilde ilişkilidir ki ortaya çıkan vektör toplamı her iki durumda da tam olarak aynı fiziksel a vektörü olur. Farklı bazlar açısından bilinen vektörlerle karşılaşmak yaygındır (örneğin, Dünya'ya sabitlenmiş bir baz ve hareket eden bir araca sabitlenmiş ikinci bir baz). Böyle bir durumda, toplama ve çıkarma gibi temel vektör işlemlerinin gerçekleştirilebilmesi için tabanlar arasında dönüşüm yapmak için bir yöntem geliştirmek gerekir. U, v, w'yi p, q, r cinsinden ifade etmenin bir yolu, iki tabanı ilişkilendiren bilgileri içeren bir yön kosinüs matrisi ile birlikte sütun matrisleri kullanmaktır. Böyle bir ifade, yukarıdaki denklemlerin yerine konulmasıyla şu şekilde oluşturulabilir ⓘ

$${\begin{aligned}u&=(p\mathbf {e} _{1}+q\mathbf {e} _{2}+r\mathbf {e} _{3})\cdot \mathbf {n} _{1},\\v&=(p\mathbf {e} _{1}+q\mathbf {e} _{2}+r\mathbf {e} _{3})\cdot \mathbf {n} _{2},\\w&=(p\mathbf {e} _{1}+q\mathbf {e} _{2}+r\mathbf {e} _{3})\cdot \mathbf {n} _{3}.\end{aligned}}$$

ⓘ

Nokta çarpımı dağıtıldığında ⓘ

$${\begin{aligned}u&=p\mathbf {e} _{1}\cdot \mathbf {n} _{1}+q\mathbf {e} _{2}\cdot \mathbf {n} _{1}+r\mathbf {e} _{3}\cdot \mathbf {n} _{1},\\v&=p\mathbf {e} _{1}\cdot \mathbf {n} _{2}+q\mathbf {e} _{2}\cdot \mathbf {n} _{2}+r\mathbf {e} _{3}\cdot \mathbf {n} _{2},\\w&=p\mathbf {e} _{1}\cdot \mathbf {n} _{3}+q\mathbf {e} _{2}\cdot \mathbf {n} _{3}+r\mathbf {e} _{3}\cdot \mathbf {n} _{3}.\end{aligned}}$$

ⓘ

Her bir nokta çarpımı benzersiz bir skaler ile değiştirildiğinde ⓘ

$${\begin{aligned}u&=c_{11}p+c_{12}q+c_{13}r,\\v&=c_{21}p+c_{22}q+c_{23}r,\\w&=c_{31}p+c_{32}q+c_{33}r,\end{aligned}}$$

ⓘ

ve bu denklemler tek bir matris denklemi olarak ifade edilebilir ⓘ

$${\begin{bmatrix}u\\v\\w\\\end{bmatrix}}={\begin{bmatrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\c_{31}&c_{32}&c_{33}\end{bmatrix}}{\begin{bmatrix}p\\q\\r\end{bmatrix}}.$$

ⓘ

Bu matris denklemi, a'nın n bazındaki skaler bileşenlerini (u, v ve w) e bazındakilerle (p, q ve r) ilişkilendirir. Her bir matris elemanı c_jk, n_j ile ek arasındaki yön kosinüsüdür. Yön kosinüsü terimi, aynı zamanda nokta çarpımlarına eşit olan iki birim vektör arasındaki açının kosinüsünü ifade eder. Bu nedenle, ⓘ

$${\begin{aligned}c_{11}&=\mathbf {n} _{1}\cdot \mathbf {e} _{1}\\c_{12}&=\mathbf {n} _{1}\cdot \mathbf {e} _{2}\\c_{13}&=\mathbf {n} _{1}\cdot \mathbf {e} _{3}\\c_{21}&=\mathbf {n} _{2}\cdot \mathbf {e} _{1}\\c_{22}&=\mathbf {n} _{2}\cdot \mathbf {e} _{2}\\c_{23}&=\mathbf {n} _{2}\cdot \mathbf {e} _{3}\\c_{31}&=\mathbf {n} _{3}\cdot \mathbf {e} _{1}\\c_{32}&=\mathbf {n} _{3}\cdot \mathbf {e} _{2}\\c_{33}&=\mathbf {n} _{3}\cdot \mathbf {e} _{3}\end{aligned}}$$

ⓘ

Toplu olarak e₁, e₂, e₃'e e temeli ve n₁, n₂, n₃'e n temeli olarak atıfta bulunarak, tüm c_jk'leri içeren matris "e'den n'ye dönüşüm matrisi" veya "e'den n'ye döndürme matrisi" (çünkü bir vektörün bir temelden diğerine "döndürülmesi" olarak düşünülebilir) veya "e'den n'ye yön kosinüs matrisi" (çünkü yön kosinüslerini içerir) olarak bilinir. Bir rotasyon matrisinin özellikleri, tersinin transpozesine eşit olacağı şekildedir. Bu, "e'den n'ye döndürme matrisinin" "n'den e'ye döndürme matrisinin" transpozu olduğu anlamına gelir. ⓘ

Bir yön kosinüs matrisinin, C, özellikleri şunlardır:

• determinant birliktir, |C| = 1;
• tersi transpozeye eşittir;
• Satırlar ve sütunlar ortogonal birim vektörlerdir, bu nedenle nokta çarpımları sıfırdır. ⓘ

Bu yöntemin avantajı, bir yön kosinüs matrisinin genellikle iki vektör tabanını ilişkilendirmek için Euler açıları veya bir kuaterniyon kullanılarak bağımsız olarak elde edilebilmesidir, böylece temel dönüşümleri yukarıda açıklanan tüm nokta çarpımlarını hesaplamak zorunda kalmadan doğrudan gerçekleştirilebilir. ⓘ

Arka arkaya birkaç matris çarpımı uygulayarak, yön kosinüsleri kümesi birbirini izleyen bazlarla ilişkili olarak bilindiği sürece herhangi bir vektör herhangi bir bazda ifade edilebilir. ⓘ

Diğer boyutlar

Çapraz ve üçlü çarpımlar haricinde, yukarıdaki formüller iki boyuta ve daha yüksek boyutlara genelleştirilebilir. Örneğin, toplama işlemi iki boyuta şu şekilde genelleştirilir

$$(a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2})+(b_{1}{\mathbf {e} }_{1}+b_{2}{\mathbf {e} }_{2})=(a_{1}+b_{1}){\mathbf {e} }_{1}+(a_{2}+b_{2}){\mathbf {e} }_{2},$$

ve dört boyutta

$${\begin{aligned}(a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2}+a_{3}{\mathbf {e} }_{3}+a_{4}{\mathbf {e} }_{4})&+(b_{1}{\mathbf {e} }_{1}+b_{2}{\mathbf {e} }_{2}+b_{3}{\mathbf {e} }_{3}+b_{4}{\mathbf {e} }_{4})=\\(a_{1}+b_{1}){\mathbf {e} }_{1}+(a_{2}+b_{2}){\mathbf {e} }_{2}&+(a_{3}+b_{3}){\mathbf {e} }_{3}+(a_{4}+b_{4}){\mathbf {e} }_{4}.\end{aligned}}$$

ⓘ

Çapraz çarpım diğer boyutlara kolayca genelleştirilemez, ancak yakından ilişkili olan dış çarpım bunu yapar ve bunun sonucu bir bivektördür. İki boyutta bu basitçe bir pseudoscalar

$$(a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2})\wedge (b_{1}{\mathbf {e} }_{1}+b_{2}{\mathbf {e} }_{2})=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.$$

ⓘ

Yedi boyutlu bir çapraz çarpım, sonucunun iki argümana ortogonal bir vektör olması bakımından çapraz çarpıma benzer; ancak bu tür olası çarpımlardan birini seçmenin doğal bir yolu yoktur. ⓘ

Fizik

Vektörlerin fizikte ve diğer bilimlerde birçok kullanımı vardır. ⓘ

Uzunluk ve birimler

Soyut vektör uzaylarında, okun uzunluğu boyutsuz bir ölçeğe bağlıdır. Örneğin bir kuvveti temsil ediyorsa, "ölçek" fiziksel boyut uzunluğu/kuvvettir. Bu nedenle, aynı boyuttaki nicelikler arasında tipik olarak ölçek tutarlılığı vardır, ancak aksi takdirde ölçek oranları değişebilir; örneğin, "1 newton" ve "5 m" 2 cm'lik bir okla temsil ediliyorsa, ölçekler sırasıyla 1 m:50 N ve 1:250'dir. Farklı boyutlardaki vektörlerin eşit uzunlukta olmasının, diyagramın temsil ettiği sistemin doğasında bulunan bir orantı sabiti olmadığı sürece özel bir önemi yoktur. Ayrıca birim vektörün uzunluğunun (uzunluk/kuvvet vb. değil, boyut uzunluğu) koordinat sistemiyle değişmeyen bir önemi yoktur. ⓘ

Vektör değerli fonksiyonlar

Genellikle fizik ve matematik alanlarında, bir vektör zaman içinde gelişir, yani bir t zaman parametresine bağlıdır. Örneğin, r bir parçacığın konum vektörünü temsil ediyorsa, r(t) parçacığın yörüngesinin parametrik bir gösterimini verir. Vektör değerli fonksiyonlar, vektörün bileşenlerinin türevi alınarak veya integrali alınarak türevlenebilir ve integre edilebilir ve kalkülüsteki tanıdık kuralların çoğu vektör değerli fonksiyonların türevi ve integrali için geçerli olmaya devam eder. ⓘ

Konum, hız ve ivme

Üç boyutlu uzayda bir x = (x₁, x₂, x₃) noktasının konumu, taban noktası orijin olan bir konum vektörü olarak gösterilebilir

$${\mathbf {x} }=x_{1}{\mathbf {e} }_{1}+x_{2}{\mathbf {e} }_{2}+x_{3}{\mathbf {e} }_{3}.$$

Konum vektörü uzunluk boyutlarına sahiptir. ⓘ

İki nokta verildiğinde x = (x₁, x₂, x₃), y = (y₁, y₂, y₃) bunların yer değiştirmesi bir vektördür

$${\mathbf {y} }-{\mathbf {x} }=(y_{1}-x_{1}){\mathbf {e} }_{1}+(y_{2}-x_{2}){\mathbf {e} }_{2}+(y_{3}-x_{3}){\mathbf {e} }_{3}.$$

Bu vektörün uzunluğu, x'ten y'ye olan düz çizgi mesafesini verir. Yer değiştirme, uzunluk boyutlarına sahiptir. ⓘ

Bir noktanın ya da parçacığın v hızı bir vektördür ve uzunluğu hızı verir. Sabit hız için t zamanındaki konum şöyle olacaktır

$${\mathbf {x} }_{t}=t{\mathbf {v} }+{\mathbf {x} }_{0},$$

Burada x₀, t = 0 zamanındaki konumdur. Hız, konumun zamana göre türevidir. Boyutları uzunluk/zamandır. ⓘ

Bir noktanın a ivmesi, hızın zaman türevi olan bir vektördür. Boyutları uzunluk/zaman²'dir. ⓘ

Kuvvet, enerji, iş

Kuvvet, kütle×uzunluk/zaman² boyutlarında bir vektördür ve Newton'un ikinci yasası skaler çarpımdır

$${\mathbf {F} }=m{\mathbf {a} }$$

ⓘ

İş, kuvvet ve yer değiştirmenin nokta çarpımıdır

$$E={\mathbf {F} }\cdot ({\mathbf {x} }_{2}-{\mathbf {x} }_{1}).$$

ⓘ

Vektörler, psödovektörler ve dönüşümler

Özellikle fizikte Öklid vektörlerinin alternatif bir nitelendirmesi, onları bir koordinat dönüşümü altında belirli bir şekilde davranan nicelikler listesi olarak tanımlar. Kontravaryant bir vektörün, baz değişiklikleri altında "bazın tersine dönüşen" bileşenlere sahip olması gerekir. Temel dönüştürüldüğünde vektörün kendisi değişmez; bunun yerine, vektörün bileşenleri temeldeki değişikliği iptal eden bir değişiklik yapar. Başka bir deyişle, referans eksenleri (ve ondan türetilen temel) bir yönde döndürülürse, vektörün bileşen temsili aynı nihai vektörü oluşturmak için ters yönde dönecektir. Benzer şekilde, referans eksenleri bir yönde gerilirse, vektörün bileşenleri tam olarak telafi edici bir şekilde azalacaktır. Matematiksel olarak, eğer temel ters çevrilebilir bir M matrisi tarafından tanımlanan bir dönüşüme uğrarsa, böylece bir x koordinat vektörü x′ = Mx olarak dönüştürülürse, o zaman bir v kontravaryant vektörü benzer şekilde v′ = M$^{-1}$v. Bu önemli gereklilik, değişmeyen bir vektörü fiziksel olarak anlamlı niceliklerin diğer herhangi bir üçlüsünden ayıran şeydir. Örneğin, eğer v hızın x, y ve z bileşenlerinden oluşuyorsa, o zaman v değişmeyen bir vektördür: uzayın koordinatları gerilir, döndürülür veya bükülürse, hızın bileşenleri de aynı şekilde dönüşür. Öte yandan, örneğin, dikdörtgen bir kutunun uzunluğu, genişliği ve yüksekliğinden oluşan bir üçlü, soyut bir vektörün üç bileşenini oluşturabilir, ancak kutuyu döndürmek kutunun uzunluğunu, genişliğini ve yüksekliğini değiştirmediğinden bu vektör değişmez olmayacaktır. Değişmez vektörlere örnek olarak yer değiştirme, hız, elektrik alanı, momentum, kuvvet ve ivme verilebilir. ⓘ

Diferansiyel geometri dilinde, bir vektörün bileşenlerinin koordinat geçişinin aynı matrisine göre dönüşmesi gerekliliği, kontravaryant bir vektörü kontravaryant rank bir tensör olarak tanımlamaya eşdeğerdir. Alternatif olarak, bir kontravaryant vektör bir teğet vektör olarak tanımlanır ve kontravaryant bir vektörü dönüştürme kuralları zincir kuralını takip eder. ⓘ

Bazı vektörler kontravaryant vektörler gibi dönüşürler, ancak bir aynadan yansıtıldıklarında ve eksi işareti kazanır. Bir aynanın yaptığı gibi sağ eli sol ele veya tersine çeviren bir dönüşümün uzayın yönünü değiştirdiği söylenir. Uzayın yönelimi değiştiğinde eksi işareti kazanan bir vektöre sahte vektör veya eksenel vektör denir. Sıradan vektörler, sözde vektörlerden ayırt etmek için bazen gerçek vektörler veya kutupsal vektörler olarak adlandırılır. Sözde vektörler en sık iki sıradan vektörün çapraz çarpımı olarak ortaya çıkar. ⓘ

Sözde vektörlere bir örnek açısal hızdır. Bir arabada giderken ve ileriye doğru bakarken, tekerleklerin her birinin solu gösteren bir açısal hız vektörü vardır. Eğer dünya, arabanın sol ve sağ tarafını değiştiren bir aynada yansıtılırsa, bu açısal hız vektörünün yansıması sağa işaret eder, ancak gerçek Tekerleğin açısal hız vektörü hala eksi işaretine karşılık gelen solu gösterir. Diğer sözde vektör örnekleri arasında manyetik alan, tork veya daha genel olarak iki (gerçek) vektörün herhangi bir çapraz çarpımı yer alır. ⓘ

Vektörler ve sahte vektörler arasındaki bu ayrım genellikle göz ardı edilir, ancak simetri özelliklerini incelerken önemli hale gelir. Bkz. parite (fizik). ⓘ

Köken

İngilizcede bu yapı için kullanılan sözcük vector dür. Kökeni, "taşımak"/"bir yöne aktarmak"/"göndermek" anlamına gelen "vehere" Latince fiil gövdesidir. Sözcüğün anlamı "taşıyıcı"/"yöncü" olarak düşünülebilir. Bu yüzden olabilir ki Türkçede (büyük ihtimalle Fransızcadan devşirilmiş olan) vektör karşılığından sonra yöney karşılığı kullanılmaktadır. ⓘ

Soyut tanımı

Soyut olarak vektörler, bir F cisminin üzerine tanımlı bir vektör uzayının öğeleridir. Vektörler bu cisim üzerine tanımlanmış bir denklik bağıntısı yardımıyla tanımlanabilir. $a,b,c,d\in F^{n}=F\times F\times \cdots \times F$ (n tane) olsun. a öğesi ile b öğesi,ancak bileşenlerin toplamı olarak a+d=b+c ise bağıntılıdır. Daha biçimsel olmak gerekirse ⓘ

$a\sim b\Leftrightarrow \forall i\in \{1,2,\cdots ,n\}:\quad a_{i}+d_{i}=b_{i}+c_{i}$ ⓘ

şeklinde tanımlanır ki burada $a_{i}\in F$'ler a noktasının koordinatlarıdır ve +işlemi F cismine aittir. ⓘ

Bu bağıntının bir denklik bağıntısı olduğu kolaylıkla görülebilir. O halde vektör, denklik sınıflarıdır. Böylece denklik sınıfı temsilcisini koyu harfle gösterirsek, bir vektör ⓘ

$\mathbf {a} =\{a|a\sim b\}$ ⓘ

olarak tanımlanmış olur. Daha açık bir biçimde bir vektör, ⓘ

$\mathbf {a} =(a_{1}-b_{1},a_{2}-b_{2},\cdots ,a_{n}-b_{n})=(c_{1}-d_{1},c_{2}-d_{2},\cdots ,c_{n}-d_{n})$ ⓘ

şeklinde düşünülebilir. ⓘ

Vektör toplamı

İki vektörün toplamı üçüncü bir vektöre eşittir. 1.şekil parelelkenar metodu,2.si ise uç uca ekleme metodudur. ⓘ

$\mathbf {a} +\mathbf {b}$	$=(a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+\cdots +a_{n}\mathbf {i} _{n})+(b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+\cdots +b_{n}\mathbf {i} _{n})$ ⓘ
	$=(a_{1}+b_{1})\mathbf {i} _{1}+(a_{2}+b_{2})\mathbf {i} _{2}+\cdots +(a_{n}+b_{n})\mathbf {i} _{n}$
	$={\begin{bmatrix}a_{1}+b_{n}\\a_{2}+b_{n}\\\cdots \\a_{3}+b_{n}\end{bmatrix}}$

Doğrudan çarpım (tensör çarpımı)

İki vektörün doğrudan çarpımının sonucu ne bir vektördür ne bir skalerdir, bir ikiçtir (dyad). ⓘ

$\mathbf {a} \mathbf {b} ={\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}{\begin{bmatrix}b_{1}&&b_{2}&&b_{3}\end{bmatrix}}={\begin{bmatrix}a_{1}b_{1}&&a_{1}b_{2}&&a_{1}b_{3}\\a_{2}b_{1}&&a_{2}b_{2}&&a_{2}b_{3}\\a_{3}b_{1}&&a_{3}b_{2}&&a_{3}b_{3}\end{bmatrix}}$

Bu çarpıma, eğer vektörler eş boyutluysa, çiftli (dyadic) çarpım denir. Eğer vektöreri birim vektörlerle ifade edersek ⓘ

$\mathbf {a} =a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+a_{3}\mathbf {i} _{3}$

$\mathbf {b} =b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+b_{3}\mathbf {i} _{3}$ ⓘ

şeklinde tanımlanan iki vektör için doğrudan çarpım ⓘ

$\mathbf {a} \mathbf {b} \,$	=	$(a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+a_{3}\mathbf {i} _{3})(b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+b_{3}\mathbf {i} _{3})$
	=	$a_{1}b_{1}\mathbf {i} _{1}\mathbf {i} _{1}+a_{1}b_{2}\mathbf {i} _{1}\mathbf {i} _{2}+a_{1}b_{3}\mathbf {i} _{1}\mathbf {i} _{3}$
	+	$a_{2}b_{1}\mathbf {i} _{2}\mathbf {i} _{1}+a_{2}b_{2}\mathbf {i} _{2}\mathbf {i} _{2}+a_{2}b_{3}\mathbf {i} _{2}\mathbf {i} _{3}$
	+	$a_{3}b_{1}\mathbf {i} _{3}\mathbf {i} _{1}+a_{3}b_{2}\mathbf {i} _{3}\mathbf {i} _{2}+a_{3}b_{3}\mathbf {i} _{3}\mathbf {i} _{3}$

ⓘ

olarak elde edilir. Buradaki $\mathbf {i} _{1}\mathbf {i} _{2}$ gibi birimler yeni birer birimdir, yâni başka bir $\mathbf {i}$ cinsinden ifade edilemez. Bu yüzden$\mathbf {i} _{ij}=\mathbf {i} _{i}\mathbf {i} _{j}$ olarak tanımlandığında ⓘ

$\quad$	=	$a_{1}b_{1}\mathbf {i} _{11}+a_{1}b_{2}\mathbf {i} _{12}+a_{1}b_{3}\mathbf {i} _{13}$
	+	$a_{2}b_{1}\mathbf {i} _{21}+a_{2}b_{2}\mathbf {i} _{22}+a_{2}b_{3}\mathbf {i} _{23}$
	+	$a_{3}b_{1}\mathbf {i} _{31}+a_{3}b_{2}\mathbf {i} _{32}+a_{3}b_{3}\mathbf {i} _{33}$

ⓘ

elde edilir ki bu da dizey gösterimine tekâbül eder. ⓘ

İç (Skaler) çarpım (G⃗ ⋅ H⃗)

Bileşenleri türünden çarpımı

Örnek:

${\overrightarrow {G}}=(a,b,c)$

${\overrightarrow {H}}=(d,e,f)$ ⓘ

Bu iki vektörü ele alırsak:

${\overrightarrow {G}}\cdot {\overrightarrow {H}}={(a,b,c)}\cdot {(d,e,f)}={a}\cdot {d}+{b}\cdot {e}+{c}\cdot {f}$ ⓘ

Aralarındaki açı türünden çarpımı

${\overrightarrow {A}}$ ve ${\overrightarrow {B}}$ vektörleri arasındaki "theta" açısı. ⓘ

Örnek:

${\overrightarrow {G}}=(a,b,c)$

${\overrightarrow {H}}=(d,e,f)$ ⓘ

Bu iki vektörü ele alırsak:

${\overrightarrow {G}}\cdot {\overrightarrow {H}}=\left\|{\overrightarrow {G}}\right\|\left\|{\overrightarrow {H}}\right\|\cos \theta$ ⓘ

$\cos \theta$ 'nın değerini bulmak için:

$\cos \theta ={\frac {{\overrightarrow {G}}\cdot {\overrightarrow {H}}}{\left\|{\overrightarrow {G}}\right\|\left\|{\overrightarrow {H}}\right\|}}$ ⓘ

Vektörel çarpım (G⃗ × H⃗)

Çapraz çarpım da denilen çarpım yöntemiyle yapılan çarpımdır. × H⃗) ⓘ

Örnek:

${\overrightarrow {G}}=(a,b,c)=a{\mathbf {i} }+b{\mathbf {j} }+c{\mathbf {k} }$

${\overrightarrow {H}}=(d,e,f)=d{\mathbf {i} }+e{\mathbf {j} }+f{\mathbf {k} }$ × H⃗) ⓘ

Bu iki vektörü ele alırsak:

${\overrightarrow {G}}\times {\overrightarrow {H}}$	$={\begin{vmatrix}\mathbf {i} &&\mathbf {j} &&\mathbf {k} \\a&&b&&c\\d&&e&&f\end{vmatrix}}$
$\quad$

× H⃗) ⓘ

Yukarıdaki problem bir determinant problemidir. Sarrus kuralı ile hesaplanır. × H⃗) ⓘ