Viskozite

Viskozite ⓘ
Viskozite ⓘ
	Farklı viskozitelere sahip sıvıların simülasyonu. Soldaki sıvı, sağdaki sıvıdan daha düşük viskoziteye sahiptir.
Ortak semboller	η, μ
Türevleri; diğer miktarlar	μ = G-t

Bir sıvının viskozitesi, belirli bir oranda deformasyona karşı direncinin bir ölçüsüdür. Sıvılar için, gayri resmi "kalınlık" kavramına karşılık gelir: örneğin, şurup sudan daha yüksek bir viskoziteye sahiptir. ⓘ

Viskozite, göreceli hareket halindeki bitişik sıvı katmanları arasındaki iç sürtünme kuvvetini ölçer. Örneğin, viskoz bir akışkan bir tüpün içinden geçmeye zorlandığında, tüpün eksenine yakın yerlerde duvarlarına yakın yerlere göre daha hızlı akar. Deneyler, akışı sürdürmek için bir miktar gerilime (tüpün iki ucu arasındaki basınç farkı gibi) ihtiyaç olduğunu göstermektedir. Bunun nedeni, göreceli hareket halindeki akışkan katmanları arasındaki sürtünmenin üstesinden gelmek için bir kuvvet gerekmesidir. Sabit akış hızına sahip bir tüp için, dengeleyici kuvvetin gücü akışkanın viskozitesi ile orantılıdır. ⓘ

Genel olarak viskozite, sıcaklık, basınç ve deformasyon oranı gibi akışkanın durumuna bağlıdır. Ancak, bu özelliklerden bazılarına olan bağımlılık bazı durumlarda ihmal edilebilir düzeydedir. Örneğin, Newtonian bir sıvının viskozitesi deformasyon oranıyla önemli ölçüde değişmez. Sıfır viskozite (kayma gerilimine direnç yok) sadece süper akışkanlarda çok düşük sıcaklıklarda gözlenir; aksi takdirde termodinamiğin ikinci yasası tüm akışkanların pozitif viskoziteye sahip olmasını gerektirir. Viskozitesi sıfır olan bir akışkan ideal veya viskoz olmayan olarak adlandırılır. ⓘ

Akmazlık değeri daha yüksek olan mor sıvı ve düşük akmazlık değerine sahip gri sıvının dökülmelerindeki fiziksel fark. Viskozitesi "düşük" olan gri sıvı daha fazla yayılım gösterecektir. ⓘ

Etimoloji

"Viskozite" kelimesi Latince viscum ("ökseotu") kelimesinden türetilmiştir. Viscum ayrıca ökse otu meyvelerinden elde edilen viskoz bir yapıştırıcıya da atıfta bulunur. ⓘ

Tanım

Dinamik viskozite

Düzlemsel bir Couette akışının gösterimi. Kesme akışına bitişik akışkan katmanları (göreceli hareket halinde olan) arasındaki sürtünme karşı çıktığından, üst plakanın hareketini sürdürmek için bir kuvvet gereklidir. Bu kuvvetin göreceli gücü akışkanın viskozitesinin bir ölçüsüdür. ⓘ

Genel bir paralel akışta, kayma gerilimi hızın gradyanı ile orantılıdır. ⓘ

Malzeme bilimi ve mühendisliğinde, genellikle bir malzemenin deformasyonunda yer alan kuvvetleri veya gerilmeleri anlamakla ilgilenilir. Örneğin, malzeme basit bir yay olsaydı, cevap Hooke yasası ile verilirdi; bu yasa, bir yayın maruz kaldığı kuvvetin dengeden uzaklaştığı mesafe ile orantılı olduğunu söyler. Bir malzemenin bazı dinlenme durumlarından deformasyonuna atfedilebilen gerilmelere elastik gerilmeler denir. Diğer malzemelerde, deformasyonun zaman içindeki değişim oranına atfedilebilecek gerilimler mevcuttur. Bunlara viskoz gerilmeler denir. Örneğin, su gibi bir akışkanda, akışkanın kesilmesinden kaynaklanan gerilmeler, akışkanın kesildiği mesafeye bağlı değildir; daha ziyade, kesilmenin ne kadar hızlı gerçekleştiğine bağlıdır. ⓘ

Viskozite, bir malzemedeki viskoz gerilmeleri bir deformasyonun değişim hızıyla (gerinim hızı) ilişkilendiren malzeme özelliğidir. Genel akışlar için geçerli olsa da, düzlemsel Couette akışı gibi basit bir kesme akışında görselleştirilmesi ve tanımlanması kolaydır. ⓘ

Couette akışında bir akışkan, biri sabit diğeri sabit hızda paralel hareket eden sonsuz büyüklükteki iki plaka arasında sıkışır $u$ (sağdaki resme bakınız). Üst plakanın hızı yeterince düşükse (türbülanstan kaçınmak için), sabit durumda akışkan parçacıkları ona paralel hareket eder ve hızları aşağıdakilerden değişir $0$ altta $u$ en üstte. Her bir sıvı katmanı hemen altındakinden daha hızlı hareket eder ve aralarındaki sürtünme, göreceli hareketlerine direnen bir kuvvete yol açar. Özellikle, akışkan üst plakaya kendi hareketinin tersi yönünde bir kuvvet uygularken, alt plakaya da eşit fakat ters yönde bir kuvvet uygular. Bu nedenle üst plakanın sabit hızda hareket etmesini sağlamak için harici bir kuvvet gereklidir. ⓘ

Birçok akışkanda, akış hızının altta sıfırdan üste doğru doğrusal olarak değiştiği gözlenir. $u$ en üstte. Dahası, kuvvetin büyüklüğü, $F$ 'nin üst plakaya etki eden hız ile orantılı olduğu bulunmuştur. $u$ ve bölge $A$ ve aralarındaki mesafe ile ters orantılıdır. $y$ :

F=\mu A{\frac {u}{y}}.

Orantılılık faktörü akışkanın dinamik viskozitesidir ve genellikle basitçe viskozite olarak adlandırılır. Yunanca mu ( $μ$ ) harfi ile gösterilir. Dinamik viskozite şu boyutlara sahiptir $\mathrm {(mass/length)/time}$ Böylece SI birimleri ve türetilmiş birimler ortaya çıkar:

[\mu ]={\frac {\rm {kg}}{\rm {m\cdot s}}}={\frac {\rm {N}}{\rm {m^{2}}}}\cdot s={\rm {Pa\cdot s}}=

basınç çarpı zaman. ⓘ

Yukarıda bahsedilen oran $u/y$ kayma deformasyon hızı veya kayma hızı olarak adlandırılır ve plakalara dik yöndeki akışkan hızının türevidir (sağdaki resimlere bakınız). Eğer hız doğrusal olarak değişmiyorsa $y$ , o zaman uygun genelleme şudur:

\tau =\mu {\frac {\partial u}{\partial y}},

nerede $\tau =F/A$ ve $\partial u/\partial y$ yerel kayma hızıdır. Bu ifade Newton'un viskozite yasası olarak adlandırılır. Düzlemsel simetriye sahip kesme akışlarında $\mu$ . Bu, koordinatsız formda ifade edilebilen genel viskozite tanımının (aşağıya bakınız) özel bir durumudur. ⓘ

Yunanca mu harfinin kullanımı ( $\mu$ ) dinamik viskozite (bazen mutlak viskozite olarak da adlandırılır) için kullanılması makine ve kimya mühendislerinin yanı sıra matematikçiler ve fizikçiler arasında da yaygındır. Bununla birlikte, Yunan harfi eta ( $\eta$ ) kimyagerler, fizikçiler ve IUPAC tarafından da kullanılmaktadır. Viskozite $\mu$ bazen kayma viskozitesi olarak da adlandırılır. Bununla birlikte, en az bir yazar bu terminolojinin kullanılmasını önermemekte ve şunları belirtmektedir $\mu$ kayma akışlarına ek olarak kayma olmayan akışlarda da ortaya çıkabilir. ⓘ

Kinematik viskozite

Akışkanlar dinamiğinde, dinamik viskozitenin ( $μ$ ) akışkan yoğunluğuna ( $ρ$ ) oranı olarak tanımlanan kinematik viskozite (bazen momentum difüzivitesi olarak da adlandırılır) açısından çalışmak bazen daha uygundur. Genellikle Yunanca nu ( $ν$ ) harfi ile gösterilir:

\nu ={\frac {\mu }{\rho }},

ⓘ

ve boyutlara sahiptir $\mathrm {(length)^{2}/time}$ Böylece SI birimleri ve türetilmiş birimler ortaya çıkar:

[\nu ]={\frac {\rm {m^{2}}}{\rm {s}}}=\mathrm {{\frac {\rm {N\cdot m}}{\rm {kg}}}\cdot s} =\mathrm {{\frac {\rm {J}}{\rm {kg}}}\cdot s} =

özgül enerjinin zamanla çarpımı. ⓘ

Genel tanım

Çok genel bir ifadeyle, bir akışkan içindeki viskoz gerilmeler, farklı akışkan parçacıklarının bağıl hızından kaynaklanan gerilmeler olarak tanımlanır. Bu nedenle, viskoz gerilmeler akış hızının uzamsal gradyanlarına bağlı olmalıdır. Eğer hız gradyanları küçükse, ilk yaklaşımda viskoz gerilmeler sadece hızın birinci türevlerine bağlıdır. (Newton akışkanları için bu aynı zamanda doğrusal bir bağımlılıktır.) Kartezyen koordinatlarda genel ilişki şu şekilde yazılabilir ⓘ

\tau _{ij}=\sum _{k}\sum _{\ell }\mu _{ijk\ell }{\frac {\partial v_{k}}{\partial r_{\ell }}},

ⓘ

nerede $\mu _{ijk\ell }$ hız gradyan tensörünü eşleyen bir viskozite tensörüdür $\partial v_{k}/\partial r_{\ell }$ viskoz gerilme tensörü üzerine $\tau _{ij}$ . Bu ifadedeki indisler 1 ile 3 arasında değişebildiğinden, 81 adet "viskozite katsayısı" vardır $\mu _{ijkl}$ toplamda. Bununla birlikte, viskozite rank-4 tensörünün izotropik olduğu varsayıldığında, bu 81 katsayı üç bağımsız parametreye indirgenir $\alpha$ , $\beta$ , $\gamma$ :

\mu _{ijk\ell }=\alpha \delta _{ij}\delta _{k\ell }+\beta \delta _{ik}\delta _{j\ell }+\gamma \delta _{i\ell }\delta _{jk},

ve ayrıca, akışkan basit rijit cisim rotasyonu geçirirken hiçbir viskoz kuvvetin ortaya çıkmayacağı varsayılır, dolayısıyla $\beta =\gamma$ geriye sadece iki bağımsız parametre kalır. En yaygın ayrıştırma standart (skaler) viskozite cinsindendir $\mu$ ve yığın viskozitesi $\kappa$ öyle ki $\alpha =\kappa -{\tfrac {2}{3}}\mu$ ve $\beta =\gamma =\mu$ . Vektör gösteriminde bu şu şekilde görünür:

{\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\dagger }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,

nerede $\mathbf {\delta }$ birim tensördür ve hançer $\dagger$ transpozeyi ifade eder. Bu denklem Newton'un viskozite yasasının genelleştirilmiş bir şekli olarak düşünülebilir. ⓘ

Yığın viskozitesi (hacim viskozitesi olarak da adlandırılır), bir akışkanın kaymasız sıkıştırılmasına veya genişlemesine direnen bir tür iç sürtünmeyi ifade eder. Bilgi $\kappa$ akışkanlar dinamiği problemlerinde sıklıkla gerekli değildir. Örneğin, sıkıştırılamaz bir akışkan $\nabla \cdot \mathbf {v} =0$ içeren terimdir ve bu nedenle $\kappa$ düşer. Üstelik, $\kappa$ olduğu için genellikle gazlar için ihmal edilebilir olduğu varsayılır. $0$ tek atomlu ideal bir gazda. İçinde bulunduğumuz bir durum $\kappa$ Stokes'un ses zayıflatma yasası tarafından tanımlanan ses ve şok dalgalarındaki enerji kaybının hesaplanması önemli olabilir, çünkü bu fenomenler hızlı genişleme ve sıkışmaları içerir. ⓘ

Viskozite için tanımlayıcı denklemler temel doğa yasaları değildir, bu nedenle bunların kullanışlılığı ve viskoziteyi ölçme veya hesaplama yöntemleri ayrı araçlar kullanılarak belirlenmelidir. Potansiyel bir sorun, viskozitenin prensipte, sistemdeki her parçacığın konumlarını ve momentumlarını kapsayan akışkanın tam mikroskobik durumuna bağlı olmasıdır. Bu kadar detaylı bilgi gerçekçi sistemlerde genellikle mevcut değildir. Bununla birlikte, belirli koşullar altında bu bilgilerin çoğunun ihmal edilebilir olduğu gösterilebilir. Özellikle, dengeye yakın ve sınırlardan uzak Newton akışkanları için (yığın hali), viskozite yalnızca yerel dengeyi tanımlayan uzaya ve zamana bağlı makroskopik alanlara (sıcaklık ve yoğunluk gibi) bağlıdır. ⓘ

Bununla birlikte, viskozite sıcaklık, basınç ve herhangi bir dış zorlamanın genliği ve frekansı gibi çeşitli sistem özelliklerine ihmal edilemez bir bağımlılık taşıyabilir. Bu nedenle, viskozitenin hassas ölçümleri yalnızca tanımlanır Belirli bir akışkan durumuna göre. Deneyler ve teorik modeller arasındaki karşılaştırmaları standartlaştırmak için, viskozite verileri bazen sıfır kesme sınırı veya (gazlar için) sıfır yoğunluk sınırı gibi ideal sınır durumlarına ekstrapole edilir. ⓘ

Momentum taşınımı

Taşıma teorisi, momentum taşınımı açısından viskozitenin alternatif bir yorumunu sağlar: viskozite, tıpkı termal iletkenliğin ısı taşınımını ve (kütle) difüzivitenin kütle taşınımını karakterize etmesi gibi, bir akışkan içindeki momentum taşınımını karakterize eden malzeme özelliğidir. Bu bakış açısı Newton'un viskozite yasasında örtük olarak yer almaktadır, $\tau =\mu (\partial u/\partial y)$ çünkü kayma gerilmesi $\tau$ momentum akısına eşdeğer birimlere sahiptir, yani birim alan başına birim zaman başına momentum. Böylece, $\tau$ 'deki momentum akışını belirttiği şeklinde yorumlanabilir. $y$ bir akışkan katmanından diğerine doğru. Newton'un viskozite yasasına göre, bu momentum akışı bir hız gradyanı boyunca gerçekleşir ve karşılık gelen momentum akışının büyüklüğü viskozite tarafından belirlenir. ⓘ

Isı ve kütle transferi ile analoji açık bir şekilde yapılabilir. Tıpkı ısının yüksek sıcaklıktan düşük sıcaklığa ve kütlenin yüksek yoğunluktan düşük yoğunluğa doğru akması gibi, momentum da yüksek hızdan düşük hıza doğru akar. Bu davranışların tümü, burada tek boyutlu formları verilen ve kurucu bağıntılar olarak adlandırılan kompakt ifadelerle tanımlanır:

{\begin{aligned}\mathbf {J} &=-D{\frac {\partial \rho }{\partial x}}&&{\text{(Fick's law of diffusion)}}\\[5pt]\mathbf {q} &=-k_{t}{\frac {\partial T}{\partial x}}&&{\text{(Fourier's law of heat conduction)}}\\[5pt]\tau &=\mu {\frac {\partial u}{\partial y}}&&{\text{(Newton's law of viscosity)}}\end{aligned}}

nerede $\rho$ yoğunluktur, $\mathbf {J}$ ve $\mathbf {q}$ kütle ve ısı akılarıdır ve $D$ ve $k_{t}$ kütle difüzivitesi ve termal iletkenliktir. Kütle, momentum ve enerji (ısı) taşınımının süreklilik mekaniğindeki en ilgili süreçler arasında yer alması bir tesadüf değildir: bunlar parçacıklar arası çarpışmalarda mikroskobik düzeyde korunan birkaç fiziksel nicelik arasındadır. Bu nedenle, hızlı ve karmaşık mikroskobik etkileşim zaman ölçeği tarafından belirlenmek yerine, dinamikleri, taşıma teorisi ve hidrodinamiğin çeşitli denklemleri tarafından tanımlandığı gibi makroskobik zaman ölçeklerinde gerçekleşir. ⓘ

Newtonyen ve Newtonyen olmayan akışkanlar

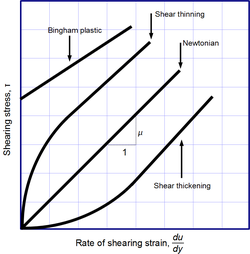
Viskozite, her bir çizginin eğimi, malzemeler arasında farklılık gösterir. ⓘ

Newton'un viskozite yasası temel bir doğa yasası değildir, daha ziyade viskoziteyi tanımlamaya yarayan kurucu bir denklemdir (Hooke yasası, Fick yasası ve Ohm yasası gibi) $\mu$ . Bu form, geniş bir akışkan yelpazesi için bunu gösteren deneylerle motive edilmiştir, $\mu$ gerinim hızından bağımsızdır. Bu tür akışkanlar Newtonian olarak adlandırılır. Gazlar, su ve birçok yaygın sıvı, olağan koşullarda ve bağlamlarda Newtonian olarak kabul edilebilir. Bununla birlikte, bu davranıştan önemli ölçüde sapan birçok Newtonyen olmayan akışkan vardır. Örneğin:

Viskozitesi kayma gerilmesi oranı ile artan kayma kalınlaşmalı (dilatant) sıvılar.
Viskozitesi kayma gerilmesi oranı ile azalan kayma inceltici sıvılar.
Tiksotropik sıvılar, çalkalandığında, çalkalandığında veya başka bir şekilde gerildiğinde zamanla daha az viskoz hale gelen sıvılar.
Çalkalandığında, çalkalandığında veya başka bir şekilde gerildiğinde zamanla daha viskoz hale gelen reopektik sıvılar.
Düşük gerilimlerde katı gibi davranan ancak yüksek gerilimlerde viskoz bir sıvı gibi akan Bingham plastikleri. ⓘ

Trouton oranı, uzama viskozitesinin kayma viskozitesine oranıdır. Newtonian bir sıvı için Trouton oranı 3'tür. Kayma inceltici sıvılar çok yaygın olarak, ancak yanıltıcı bir şekilde tiksotropik olarak tanımlanır. ⓘ

Newtonian bir akışkan için bile viskozite genellikle bileşimine ve sıcaklığa bağlıdır. Gazlar ve diğer sıkıştırılabilir akışkanlar için sıcaklığa bağlıdır ve basınçla çok yavaş değişir. Bazı akışkanların viskozitesi başka faktörlere de bağlı olabilir. Örneğin manyetoreolojik bir sıvı, manyetik bir alana maruz kaldığında muhtemelen katı gibi davranacak kadar kalınlaşır. ⓘ

Katılarda

Akışkan akışı sırasında ortaya çıkan viskoz kuvvetler, bir katı maddede kesme, sıkıştırma veya uzama gerilmelerine tepki olarak ortaya çıkan elastik kuvvetlerden farklıdır. İkincisinde stres kayma deformasyonunun miktarı ile orantılı iken, bir akışkanda zaman içindeki deformasyon oranı ile orantılıdır. Bu nedenle Maxwell, akışkan viskozitesi için kaçak elastikiyet terimini kullanmıştır. ⓘ

Bununla birlikte, birçok sıvı (su dahil) ani bir gerilime maruz kaldığında kısa süreliğine elastik katılar gibi tepki verir. Tersine, birçok "katı" (granit bile), keyfi olarak küçük stres altında bile çok yavaş da olsa sıvılar gibi akacaktır. Bu tür malzemeler en iyi viskoelastik olarak tanımlanır; yani hem elastikiyete (deformasyona tepki) hem de viskoziteye (deformasyon oranına tepki) sahiptir. ⓘ

Viskoelastik katılar hem kayma viskozitesi hem de yığın viskozitesi sergileyebilir. Uzama viskozitesi, katı elastik bir malzemenin uzamaya karşı tepkisini tanımlayan kesme ve yığın viskozitelerinin doğrusal bir kombinasyonudur. Polimerleri karakterize etmek için yaygın olarak kullanılır. ⓘ

Jeolojide, elastik deformasyonlarından en az üç mertebe daha büyük viskoz deformasyon sergileyen toprak malzemelerine bazen reidler denir. ⓘ

Ölçüm

Viskozite, çeşitli viskozimetreler ve reometreler ile ölçülür. Reometre, tek bir viskozite değeriyle tanımlanamayan ve bu nedenle viskozimetrede olduğundan daha fazla parametrenin ayarlanmasını ve ölçülmesini gerektiren akışkanlar için kullanılır. Özellikle viskozitesi sadece 5 °C'lik bir değişimle iki katına çıkabilen yağlayıcılar gibi malzemelerde doğru ölçümler elde etmek için akışkanın yakın sıcaklık kontrolü şarttır. ⓘ

Bazı akışkanlar için viskozite geniş bir kayma hızı aralığında sabittir (Newtonian akışkanlar). Sabit viskozitesi olmayan akışkanlar (Newtonyen olmayan akışkanlar) tek bir sayı ile tanımlanamaz. Newtonyen olmayan akışkanlar, kayma gerilimi ve kayma hızı arasında çeşitli farklı korelasyonlar sergiler. ⓘ

Kinematik viskoziteyi ölçmek için kullanılan en yaygın cihazlardan biri cam kapiler viskozimetredir. ⓘ

Kaplama endüstrilerinde viskozite, akış süresinin ölçüldüğü bir kap ile ölçülebilir. Zahn kabı ve Ford viskozite kabı gibi çeşitli kap türleri vardır ve her bir türün kullanımı esas olarak endüstriye göre değişir. ⓘ

Kaplamalarda da kullanılan Stormer viskozimetre, viskoziteyi belirlemek için yük bazlı rotasyon kullanır. Viskozite, Stormer viskozimetrelerine özgü olan Krebs birimleri (KU) cinsinden raporlanır. ⓘ

Titreşimli viskozimetreler de viskoziteyi ölçmek için kullanılabilir. Rezonans veya titreşimli viskozimetreler sıvı içinde kesme dalgaları oluşturarak çalışır. Bu yöntemde sensör sıvıya daldırılır ve belirli bir frekansta rezonansa girmesi sağlanır. Sensörün yüzeyi sıvıyı keserken, viskozitesi nedeniyle enerji kaybedilir. Kaybedilen bu enerji daha sonra ölçülür ve viskozite değerine dönüştürülür. Daha yüksek viskozite daha fazla enerji kaybına neden olur. ⓘ

Ekstensiyonel viskozite, ekstensiyonel stres uygulayan çeşitli reometrelerle ölçülebilir. ⓘ

Hacimsel viskozite akustik reometre ile ölçülebilir. ⓘ

Görünür viskozite, petrol veya gaz kuyusu geliştirmede kullanılan sondaj sıvısı üzerinde yapılan testlerden elde edilen bir hesaplamadır. Bu hesaplamalar ve testler, mühendislerin sondaj sıvısının özelliklerini gerekli spesifikasyonlara göre geliştirmelerine ve korumalarına yardımcı olur. ⓘ

Nanoviskozite (nanoproblar tarafından algılanan viskozite) floresan korelasyon spektroskopisi ile ölçülebilir. ⓘ

Birimler

SI dinamik viskozite birimi metrekare başına newton-saniye (N-s/m²) olup, sıklıkla paskal-saniye (Pa-s), metre/saniye başına kilogram (kg-m-1-s-1) ve Poiseuilli (Pl) eşdeğer formlarında da ifade edilir. CGS birimi, adını Jean Léonard Marie Poiseuille'den alan poise (P veya g-cm-1-s-1 = 0,1 Pa-s) birimidir. Özellikle ASTM standartlarında yaygın olarak santipoise (cP) olarak ifade edilir. Santipoise uygundur çünkü suyun 20 °C'deki viskozitesi yaklaşık 1 cP'dir ve bir santipoise SI millipascal saniyeye (mPa-s) eşittir. ⓘ

Kinematik viskozitenin SI birimi saniye başına metrekaredir (m²/s), kinematik viskozite için CGS birimi ise adını Sir George Gabriel Stokes'tan alan stokes (St veya cm²-s-1 = 0,0001 m²-s-1) birimidir. ABD kullanımında stoke bazen tekil form olarak kullanılır. Bunun yerine genellikle santistok (cSt) alt katsayısı kullanılır. 1 cSt = 1 mm²-s-1 = 10-6 m²-s-1. Suyun 20 °C'deki kinematik viskozitesi yaklaşık 1 cSt'dir. ⓘ

ABD geleneksel veya İmparatorluk birimlerinin en sık kullanılan sistemleri İngiliz Yerçekimi (BG) ve İngiliz Mühendislik (EE) sistemleridir. BG sisteminde dinamik viskozite feet kare başına pound-saniye (lb-s/ft²) birimine sahiptir ve EE sisteminde feet kare başına pound-kuvvet-saniye (lbf-s/ft²) birimine sahiptir. Pound ve pound-kuvvet eşdeğerdir; iki sistem sadece kuvvet ve kütlenin nasıl tanımlandığı konusunda farklılık gösterir. BG sisteminde pound, kütle biriminin (sümüklü böcek) Newton'un İkinci Yasası ile tanımlandığı temel bir birimken, EE sisteminde kuvvet ve kütle birimleri (sırasıyla pound-kuvvet ve pound-kütle) orantılılık sabiti gc kullanılarak İkinci Yasa aracılığıyla bağımsız olarak tanımlanır. ⓘ

Kinematik viskozite hem BG hem de EE sistemlerinde feet kare/saniye (ft²/s) birimine sahiptir. ⓘ

Standart olmayan birimler arasında bir İngiliz dinamik viskozite birimi olan reyn de bulunmaktadır. Otomotiv endüstrisinde viskozite indeksi, viskozitenin sıcaklıkla değişimini tanımlamak için kullanılır. ⓘ

Viskozitenin karşılığı akışkanlıktır ve genellikle şu şekilde sembolize edilir $\phi =1/\mu$ veya $F=1/\mu$ kullanılan konvansiyona bağlı olarak, karşılıklı poise (P-1 veya cm-s-g-1) cinsinden ölçülür, bazen rhe olarak adlandırılır. Akışkanlık mühendislik uygulamalarında nadiren kullanılır. ⓘ

Bir zamanlar petrol endüstrisi kinematik viskoziteyi Saybolt viskozimetresi ile ölçmeye ve kinematik viskoziteyi Saybolt evrensel saniye (SUS) birimleriyle ifade etmeye dayanıyordu. SSU (Saybolt saniye evrensel) veya SUV (Saybolt evrensel viskozite) gibi diğer kısaltmalar da bazen kullanılmaktadır. Santistok cinsinden kinematik viskozite, ASTM D 2161'de sağlanan aritmetik ve referans tablosuna göre SUS'den dönüştürülebilir. ⓘ

Moleküler kökenler

Gazlarda momentum taşınımına ayrık moleküler çarpışmalar, sıvılarda ise molekülleri birbirine yakın bağlayan çekici kuvvetler aracılık eder. Bu nedenle, sıvıların dinamik viskoziteleri tipik olarak gazlarınkinden çok daha büyüktür. Ayrıca viskozite, gazlarda sıcaklıkla birlikte artma eğilimindeyken sıvılarda sıcaklıkla birlikte azalır. ⓘ

Sıvı-gaz kritik noktasının üzerinde, sıvı ve gaz fazları tek bir süperkritik faz ile yer değiştirir. Bu rejimde, momentum taşıma mekanizmaları sıvı benzeri ve gaz benzeri davranışlar arasında geçiş yapar. Örneğin, süperkritik bir izobar (sabit basınçlı yüzey) boyunca kinematik viskozite düşük sıcaklıkta azalır ve yüksek sıcaklıkta artar, arada bir minimum olur. Değer için kabaca bir tahmin minimumda

\nu _{\text{min}}={\frac {1}{4\pi }}{\frac {\hbar }{\sqrt {m_{e}m}}}

nerede $\hbar$ Planck sabitidir, $m_{e}$ elektron kütlesidir ve $m$ moleküler kütledir. ⓘ

Bununla birlikte, genel olarak, bir sistemin viskozitesi, sistemi oluşturan moleküllerin nasıl etkileşime girdiğine ayrıntılı olarak bağlıdır ve bunun için basit ama doğru formüller yoktur. En basit kesin ifadeler, doğrusal kayma viskozitesi için Green-Kubo ilişkileri veya Evans ve Morriss tarafından 1988 yılında türetilen geçici zaman korelasyon fonksiyonu ifadeleridir. Bu ifadelerin her biri kesin olmasına rağmen, bu ilişkileri kullanarak yoğun bir sıvının viskozitesini hesaplamak şu anda moleküler dinamik bilgisayar simülasyonlarının kullanılmasını gerektirmektedir. Seyreltik bir gaz için biraz daha fazla ilerleme kaydedilebilir, çünkü gaz moleküllerinin nasıl hareket ettiği ve etkileştiği hakkındaki temel varsayımlar viskozitenin moleküler kökenlerinin temel bir şekilde anlaşılmasını sağlar. Gaz moleküllerinin hareket denklemleri sistematik olarak kaba tanecikli hale getirilerek daha sofistike uygulamalar oluşturulabilir. Böyle bir uygulamaya örnek olarak, Boltzmann denkleminden seyreltik bir gazın viskozitesi için ifadeler türeten Chapman-Enskog teorisi verilebilir. ⓘ

Saf gazlar

Seyreltik bir gaz için temel viskozite hesaplaması

'ye paralel hareket eden seyreltik bir gaz düşünün. $x$ hız ile -ekseni $u(y)$ Bu sadece $y$ Koordinat. Tartışmayı basitleştirmek için gazın tek tip sıcaklık ve yoğunluğa sahip olduğu varsayılmıştır. ⓘ

Bu varsayımlar altında $x$ içinden geçen bir molekülün hızı $y=0$ o molekülün ortalama serbest yol katettiğinde sahip olduğu hıza eşittir $\lambda$ başladı. Çünkü $\lambda$ makroskopik ölçeklerle karşılaştırıldığında tipik olarak küçüktür, ortalama $x$ Böyle bir molekülün hızı şu şekildedir ⓘ

u(0)\pm \alpha \lambda {\frac {du}{dy}}(0),

ⓘ

nerede $\alpha$ mertebesinde sayısal bir sabittir. $1$ . (Bazı yazarların tahminine göre $\alpha =2/3$ Öte yandan, rijit elastik küreler için daha dikkatli bir hesaplama $\alpha \simeq 0.998$ .) Daha sonra, her iki taraftaki moleküllerin yarısı $y=0$ ve bunu ortalama olarak ortalama moleküler hızın yarısı ile yapar $(8k_{\text{B}}T/\pi m)^{1/2}$ her iki taraftan gelen momentum akısı ise ⓘ

{\frac {1}{4}}\rho \cdot {\sqrt {\frac {8k_{\text{B}}T}{\pi m}}}\cdot \left(u(0)\pm \alpha \lambda {\frac {du}{dy}}(0)\right).

'deki net momentum akısı $y=0$ ikisinin farkıdır:

-{\frac {1}{2}}\rho \cdot {\sqrt {\frac {8k_{\text{B}}T}{\pi m}}}\cdot \alpha \lambda {\frac {du}{dy}}(0).

ⓘ

Viskozite tanımına göre, bu momentum akısı aşağıdakilere eşit olmalıdır $-\mu {\frac {du}{dy}}(0)$ 'ye yol açar. ⓘ

\mu =\alpha \rho \lambda {\sqrt {\frac {2k_{\text{B}}T}{\pi m}}}.

ⓘ

Gazlardaki viskozite esas olarak momentumu akış katmanları arasında taşıyan moleküler difüzyondan kaynaklanır. Sıcaklıktaki seyreltik bir gaz için temel bir hesaplama $T$ ve yoğunluk $\rho$ verir

\mu =\alpha \rho \lambda {\sqrt {\frac {2k_{\text{B}}T}{\pi m}}},

ⓘ

nerede $k_{\text{B}}$ Boltzmann sabitidir, $m$ moleküler kütle ve $\alpha$ mertebesinde sayısal bir sabittir. $1$ . Miktar $\lambda$ ortalama serbest yol, bir molekülün çarpışmalar arasında kat ettiği ortalama mesafeyi ölçer. Önceden bir bilgi olmadan bile $\alpha$ bu ifadenin önemsiz sonuçları vardır. Özellikle de $\lambda$ tipik olarak yoğunluk ile ters orantılıdır ve sıcaklık ile artar, $\mu$ kendisi sıcaklıkla artmalı ve sabit sıcaklıkta yoğunluktan bağımsız olmalıdır. Aslında, bu tahminlerin her ikisi de daha sofistike uygulamalarda devam eder ve deneysel gözlemleri doğru bir şekilde tanımlar. Buna karşın, sıvı viskozitesi tipik olarak sıcaklıkla birlikte azalır. ⓘ

Çapı katı elastik küreler için $\sigma$ , $\lambda$ hesaplanabilir, bu da ⓘ

\mu ={\frac {\alpha }{\pi ^{3/2}}}{\frac {\sqrt {k_{\text{B}}mT}}{\sigma ^{2}}}.

ⓘ

Bu durumda $\lambda$ sıcaklıktan bağımsızdır, bu nedenle $\mu \propto T^{1/2}$ . Ancak daha karmaşık moleküler modeller için, $\lambda$ sıcaklığa önemsiz olmayan bir şekilde bağlıdır ve burada kullanılan basit kinetik argümanlar yetersizdir. Daha temel olarak, ortalama serbest yol kavramı, sonlu bir aralıkta etkileşime giren parçacıklar için kesin değildir, bu da kavramın gerçek dünya gazlarını tanımlamak için kullanışlılığını sınırlar. ⓘ

Chapman-Enskog teorisi

1900'lerin başında Sydney Chapman ve David Enskog tarafından geliştirilen bir teknik, aşağıdaki değerlerin daha rafine bir şekilde hesaplanmasını sağlar $\mu$ . Moleküller arası etkileşimler açısından seyreltik bir gazın istatistiksel bir tanımını sağlayan Boltzmann denklemine dayanmaktadır. Bu teknik aşağıdakilerin doğru hesaplanmasını sağlar $\mu$ moleküller arası çekimleri içerenler gibi katı elastik kürelerden daha gerçekçi moleküler modeller için. Bunu yapmak, doğru sıcaklık bağımlılığını yeniden üretmek için gereklidir. $\mu$ 'den daha hızlı arttığını göstermektedir. $T^{1/2}$ katı elastik küreler için öngörülen eğilim. Gerçekten de Chapman-Enskog analizi, öngörülen sıcaklık bağımlılığının çeşitli moleküler modellerdeki parametreler değiştirilerek ayarlanabileceğini göstermektedir. Basit bir örnek, zayıf karşılıklı çekime sahip katı elastik küreleri tanımlayan Sutherland modelidir. Böyle bir durumda, çekici kuvvet pertürbatif olarak ele alınabilir ve bu da aşağıdakiler için basit bir ifadeye yol açar $\mu$ :

\mu ={\frac {5}{16\sigma ^{2}}}\left({\frac {k_{\text{B}}mT}{\pi }}\right)^{1/2}\left(1+{\frac {S}{T}}\right)^{-1},

nerede $S$ sıcaklıktan bağımsızdır ve sadece moleküller arası çekimin parametreleri tarafından belirlenir. Deney ile bağlantı kurmak için şu şekilde yeniden yazmak uygundur

\mu =\mu _{0}\left({\frac {T}{T_{0}}}\right)^{3/2}{\frac {T_{0}+S}{T+S}},

nerede $\mu _{0}$ sıcaklıktaki viskozitedir $T_{0}$ . Eğer $\mu$ 'deki deneylerden bilinmektedir. $T=T_{0}$ ve en az bir başka sıcaklık varsa, o zaman $S$ hesaplanabilir. Şunlar için ifadeler $\mu$ Bu şekilde elde edilen potansiyeller bir dizi basit gaz için niteliksel olarak doğrudur. Lennard-Jones potansiyeli gibi biraz daha sofistike modeller, deneylerle daha iyi bir uyum sağlayabilir, ancak sadece sıcaklığa daha opak bir bağımlılık pahasına. H₂O gibi oldukça polar moleküllere sahip buharlarda olduğu gibi, bazı sistemlerde küresel simetri varsayımı da terk edilmelidir. Bu durumlarda Chapman-Enskog analizi önemli ölçüde daha karmaşıktır. ⓘ

Yığın viskozitesi

Kinetik-moleküler resimde, moleküllerin öteleme enerjisi ile dönme ve titreşim gibi iç enerjileri arasındaki enerji alışverişini yöneten ihmal edilemez gevşeme zaman ölçekleri olduğunda, gazlarda sıfır olmayan bir yığın viskozitesi ortaya çıkar. Bu nedenle, yığın viskozitesi $0$ Moleküllerin iç enerjisinin ihmal edilebilir olduğu tek atomlu ideal bir gaz için, ancak molekülleri hem dönme hem de titreşim enerjisine sahip olan karbondioksit gibi bir gaz için sıfır değildir. ⓘ

Saf sıvılar

Farklı viskozitelere sahip üç sıvıyı gösteren video ⓘ

Görünürlük için mavi boya içeren viskoz bir sıvının davranışını gösteren deney ⓘ

Gazların aksine, sıvılarda viskozitenin moleküler kökenleri için basit ama doğru bir resim yoktur. ⓘ

En basit açıklama düzeyinde, bir sıvıdaki bitişik katmanların göreceli hareketine öncelikle çekici moleküler kuvvetler karşı koyar katman sınırı boyunca hareket eder. Bu resimde (doğru olarak) viskozitenin artan sıcaklıkla birlikte azalması beklenir. Bunun nedeni Artan sıcaklık moleküllerin rastgele termal hareketini artırır, bu da çekici etkileşimlerinin üstesinden gelmelerini kolaylaştırır. ⓘ

Bu görselleştirmeye dayanarak, bir katının ayrık yapısına benzer şekilde basit bir teori oluşturulabilir: bir sıvıdaki molekül grupları tek molekülleri çevreleyen ve içine alan "kafesler" oluşturacak şekilde görselleştirilir. Bu kafesler dolu ya da boş olabilir ve Daha güçlü moleküler çekim, daha güçlü kafeslere karşılık gelir. Rastgele termal hareket nedeniyle bir molekül, moleküler çekim gücüyle ters orantılı olarak değişen bir oranda kafesler arasında "zıplar". Dengede bu "zıplamalar" herhangi bir yöne doğru eğimli değildir. Öte yandan, iki bitişik katmanın birbirine göre hareket edebilmesi için, "zıplamalar" şu yönde eğimli olmalıdır bağıl hareketin. Bu yönlendirilmiş hareketi sürdürmek için gereken kuvvet, belirli bir kayma oranı için tahmin edilebilir ve şu sonucu verir ⓘ

\mu \approx {\frac {N_{A}h}{V}}\operatorname {exp} \left(3.8{\frac {T_{b}}{T}}\right),

(1) ⓘ

nerede $N_{A}$ Avogadro sabitidir, $h$ Planck sabitidir, $V$ bir mol sıvının hacmidir ve $T_{b}$ normal kaynama noktasıdır. Bu sonuç, iyi bilinen ampirik bağıntı ile aynı biçime sahiptir ⓘ

\mu =Ae^{B/T},

(2) ⓘ

nerede $A$ ve $B$ verilerden elde edilen sabitlerdir. Öte yandan, bazı yazarlar bu modelle ilgili olarak dikkatli olunması gerektiğini ifade etmektedir. Denklem (2)'nin deneysel verilere uydurulmasıyla karşılaştırıldığında, denklem (1) kullanılarak %30'a varan hatalarla karşılaşılabilir. Daha temel olarak, denklem (1)'in altında yatan fiziksel varsayımlar eleştirilmiştir. Ayrıca denklem (1)'deki üstel bağımlılığın deneysel gözlemleri daha basit, üstel olmayan ifadelerden daha doğru bir şekilde tanımlamadığı da ileri sürülmüştür. ⓘ

Bu eksiklikler ışığında, daha az geçici bir modelin geliştirilmesi pratik bir ilgi konusudur. Hassasiyet lehine basitlikten vazgeçerek, moleküller için temel hareket denklemlerinden başlayarak viskozite için titiz ifadeler yazmak mümkündür. Klasik bir örnek Irving-Kirkwood teorisidir. Öte yandan, bu tür ifadeler çok parçacıklı korelasyon fonksiyonlarının ortalamaları olarak verilir ve bu nedenle pratikte uygulanması zordur. ⓘ

Genel olarak, deneysel olarak türetilmiş ifadeler (mevcut viskozite ölçümlerine dayalı olarak) sıvılarda viskoziteyi hesaplamanın tek tutarlı ve güvenilir yolu olarak görünmektedir. ⓘ

Karışımlar ve harmanlar

Gaz karışımları

Tek bileşenli bir gazın aynı moleküler-kinetik resmi, gaz halindeki bir karışıma da uygulanabilir. Örneğin, Chapman-Enskog yaklaşımında viskozite $\mu _{\text{mix}}$ ikili bir gaz karışımının viskozitesi, bileşenlerin ayrı ayrı viskoziteleri cinsinden yazılabilir $\mu _{1,2}$ , ilgili hacim oranları ve moleküller arası etkileşimler. Tek bileşenli gaz için olduğu gibi $\mu _{\text{mix}}$ Moleküller arası etkileşimlerin parametreleri, temel fonksiyonlar cinsinden ifade edilemeyebilecek çeşitli çarpışma integralleri yoluyla girer. Kullanılabilir ifadeler elde etmek için $\mu _{\text{mix}}$ Deneysel verilerle makul ölçüde eşleşen çarpışma integralleri tipik olarak analitik hesaplama ve ampirik uydurmanın bir kombinasyonu kullanılarak değerlendirilmelidir. Bu tür bir prosedüre örnek olarak yukarıda tartışılan tek bileşenli gaz için Sutherland yaklaşımı verilebilir. ⓘ

Sıvıların karışımları

Saf sıvılarda olduğu gibi, bir sıvı karışımının viskozitesini moleküler prensiplerden tahmin etmek zordur. Bir yöntem, yukarıda saf bir sıvı için sunulan moleküler "kafes" teorisini genişletmektir. Bu, çeşitli karmaşıklık düzeylerinde yapılabilir. Böyle bir analizden elde edilen bir ifade, ikili bir karışım için Lederer-Roegiers denklemidir:

\ln \mu _{\text{blend}}={\frac {x_{1}}{x_{1}+\alpha x_{2}}}\ln \mu _{1}+{\frac {\alpha x_{2}}{x_{1}+\alpha x_{2}}}\ln \mu _{2},

ⓘ

nerede $\alpha$ ampirik bir parametredir ve $x_{1,2}$ ve $\mu _{1,2}$ bileşen sıvıların ilgili mol kesirleri ve viskoziteleridir. ⓘ

Karıştırma, yağlama ve yağ endüstrilerinde önemli bir süreç olduğundan, bir karışımın viskozitesini tahmin etmek için çeşitli ampirik ve özel denklemler mevcuttur. ⓘ

Çözeltiler ve süspansiyonlar

Sulu çözeltiler

Çözünen maddeye ve konsantrasyon aralığına bağlı olarak, sulu bir elektrolit çözeltisi aynı sıcaklık ve basınçtaki saf su ile karşılaştırıldığında daha büyük veya daha küçük bir viskoziteye sahip olabilir. Örneğin, %20'lik bir tuzlu su (sodyum klorür) çözeltisi saf suyun 1,5 katından fazla viskoziteye sahipken, %20'lik bir potasyum iyodür çözeltisi saf suyun yaklaşık 0,91 katı viskoziteye sahiptir. ⓘ

Seyreltik elektrolitik çözeltilerin idealleştirilmiş bir modeli, viskozite için aşağıdaki tahmine yol açar $\mu _{s}$ bir çözeltinin:

{\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}},

nerede $\mu _{0}$ çözücünün viskozitesidir, $c$ konsantrasyondur ve $A$ hem çözücü hem de çözünen özelliklerine bağlı olan pozitif bir sabittir. Bununla birlikte, bu ifade yalnızca çok seyreltik çözeltiler için geçerlidir. $c$ 0,1 mol/L'den daha az. Daha yüksek konsantrasyonlar için, daha yüksek dereceli moleküler korelasyonları hesaba katan ek terimler gereklidir:

{\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}}+Bc+Cc^{2},

nerede $B$ ve $C$ verilere uymaktadır. Özellikle, negatif bir değer $B$ bazı çözeltilerde gözlenen viskozite düşüşünü açıklayabilmektedir. Bu sabitlerin tahmini değerleri 25 °C sıcaklıkta sodyum klorür ve potasyum iyodür için aşağıda gösterilmiştir (mol = mol, L = litre). ⓘ

Çözünen madde	$A$ (mol-1/2 L^1/2)	$B$ (mol-1 L)	$C$ (mol-2 L²) ⓘ
Sodyum klorür (NaCl)	0.0062	0.0793	0.0080
Potasyum iyodür (KI)	0.0047	−0.0755	0.0000

Süspansiyonlar

Katı parçacıklardan oluşan bir süspansiyonda (örneğin, yağ içinde asılı mikron boyutunda küreler), etkili bir viskozite $\mu _{\text{eff}}$ süspansiyon halindeki partiküller arasındaki mesafeye kıyasla büyük, ancak makroskopik boyutlara göre küçük bir hacim üzerinde ortalaması alınan gerilme ve gerinim bileşenleri cinsinden tanımlanabilir. Bu tür süspansiyonlar genellikle Newtonyen olmayan davranış sergiler. Bununla birlikte, kararlı akışlardaki seyreltik sistemler için davranış Newtonyen'dir ve $\mu _{\text{eff}}$ doğrudan parçacık dinamiklerinden türetilebilir. Çok seyreltik bir sistemde, hacim fraksiyonu ile $\phi \lesssim 0.02$ Asılı parçacıklar arasındaki etkileşimler göz ardı edilebilir. Böyle bir durumda, her bir parçacığın etrafındaki akış alanı bağımsız olarak açıkça hesaplanabilir ve sonuçlar birleştirilerek aşağıdakiler elde edilebilir $\mu _{\text{eff}}$ . Küreler için bu Einstein denklemiyle sonuçlanır:

\mu _{\text{eff}}=\mu _{0}\left(1+{\frac {5}{2}}\phi \right),

ⓘ

nerede $\mu _{0}$ süspansiyon halindeki sıvının viskozitesidir. Doğrusal bağımlılık $\phi$ parçacıklar arası etkileşimlerin ihmal edilmesinin bir sonucudur. Genel olarak seyreltik sistemler için $\mu _{\text{eff}}$ formunu almak için ⓘ

\mu _{\text{eff}}=\mu _{0}\left(1+B\phi \right),

ⓘ

burada katsayı $B$ parçacık şekline (örneğin küreler, çubuklar, diskler) bağlı olabilir. Kesin değerinin deneysel olarak belirlenmesi $B$ ancak zordur: tahmin bile $B=5/2$ küreler için kesin olarak doğrulanmamıştır, çeşitli deneyler aralıkta değerler bulmuştur $1.5\lesssim B\lesssim 5$ . Bu eksiklik, deneysel koşulların kontrol edilmesindeki zorluğa bağlanmıştır. ⓘ

Daha yoğun süspansiyonlarda, $\mu _{\text{eff}}$ üzerinde doğrusal olmayan bir bağımlılık kazanır $\phi$ Bu da parçacıklar arası etkileşimlerin önemini gösterir. Bu rejimi yakalamak için çeşitli analitik ve yarı ampirik şemalar mevcuttur. En temel düzeyde, ikinci dereceden bir terim $\phi$ eklenir $\mu _{\text{eff}}$ :

\mu _{\text{eff}}=\mu _{0}\left(1+B\phi +B_{1}\phi ^{2}\right),

ⓘ

ve katsayısı $B_{1}$ deneysel verilerden uyarlanır veya mikroskobik teoriden yaklaşık olarak tahmin edilir. Bununla birlikte, bazı yazarlar yoğun süspansiyonlarda Newtonyen olmayan davranışlar ortaya çıktığı için bu tür basit formüllerin uygulanmasında dikkatli olunmasını tavsiye etmektedir ( $\phi \gtrsim 0.25$ küreler için) veya uzun veya esnek parçacıkların süspansiyonlarında. ⓘ

Yukarıda tanımlanan katı parçacık süspansiyonu ile emülsiyon arasında bir ayrım vardır. İkincisi, iç sirkülasyon sergileyebilen küçük damlacıklardan oluşan bir süspansiyondur. İç sirkülasyonun varlığı gözlenen etkin viskoziteyi azaltabilir ve farklı teorik veya yarı ampirik modeller kullanılmalıdır. ⓘ

Amorf malzemeler

Yaygın cam viskozite eğrileri ⓘ

Yüksek ve düşük sıcaklık sınırlarında, amorf malzemelerdeki (örneğin camlar ve eriyiklerdeki) viskoz akış Arrhenius formuna sahiptir:

\mu =Ae^{Q/(RT)},

ⓘ

Burada $Q$ moleküler parametreler cinsinden verilen ilgili bir aktivasyon enerjisidir; $T$ sıcaklıktır; $R$ molar gaz sabitidir; ve A yaklaşık olarak bir sabittir. Aktivasyon enerjisi $Q$ , yüksek veya düşük sıcaklık sınırının dikkate alınmasına bağlı olarak farklı bir değer alır: düşük sıcaklıklarda (camsı halde) yüksek bir değer olan $Q H$ 'den yüksek sıcaklıklarda (sıvı halde) düşük bir değer olan $Q L$ 'ye değişir. ⓘ

İki rejimi gösteren B₂O₃ için sıcaklığa karşı viskozitenin ortak logaritması ⓘ

Ara sıcaklıklar için, $Q$ sıcaklıkla önemsiz bir şekilde değişir ve basit Arrhenius formu başarısız olur. Öte yandan, iki üstel denklem ⓘ

\mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\right],

ⓘ

nerede $A$ , $B$ , $C$ , $D$ tüm sabitlerdir, tüm sıcaklık aralığında deneysel verilere iyi bir uyum sağlarken, aynı zamanda düşük ve yüksek sıcaklık sınırlarında doğru Arrhenius formuna indirgenir. Bu ifade, atomik düzeyde amorf malzemelerin çeşitli teorik modellerinden motive edilebilir. ⓘ

Viskozite için iki üstel bir denklem, Arrhenius enerji bariyerinin yüksek frekanslı kesme modülü çarpı karakteristik bir itme hacmi ile tanımlandığı aşırı soğutulmuş sıvıların Dyre itme modeli içinde türetilebilir. Termal genleşme ve moleküller arası potansiyelin itici kısmı aracılığıyla kayma modülünün sıcaklığa bağımlılığı belirlendikten sonra, başka bir iki üstel denklem elde edilir:

\mu =\exp {\left\{{\frac {V_{c}C_{G}}{k_{B}T}}\exp {\left[(2+\lambda )\alpha _{T}T_{g}\left(1-{\frac {T}{T_{g}}}\right)\right]}\right\}}

ⓘ

nerede $C_{G}$ camsı geçiş sıcaklığına eşit bir sıcaklıkta değerlendirilen malzemenin yüksek frekanslı kayma modülünü ifade eder $T_{g}$ , $V_{c}$ itme hacmi olarak adlandırılır, yani bir atomun/molekülün en yakın komşularının kafesinden kaçtığı itme olayına dahil olan atom grubunun karakteristik hacmidir, tipik olarak birkaç atom tarafından işgal edilen hacim mertebesindedir. Ayrıca, $\alpha _{T}$ malzemenin termal genleşme katsayısıdır, $\lambda$ radyal dağılım fonksiyonunun ilk tepe noktasının yükselen kanadının güç kanunu yükselişinin dikliğini ölçen bir parametredir ve atomlar arası potansiyelin itici kısmıyla niceliksel olarak ilişkilidir. Son olarak, $k_{B}$ Boltzmann sabitini ifade eder. ⓘ

Eddy viskozitesi

Akışkanlardaki türbülans çalışmalarında, yaygın bir pratik strateji, hareketteki küçük ölçekli girdapları (veya girdapları) göz ardı etmek ve daha küçük ölçekli akıştaki enerjinin taşınmasını ve dağılmasını karakterize eden "girdap viskozitesi" adı verilen etkili bir viskoziteye sahip büyük ölçekli bir hareketi hesaplamaktır (bkz. büyük girdap simülasyonu). Termodinamiğin ikinci yasası gereği pozitif olması gereken akışkanın kendi viskozitesinin aksine, girdap viskozitesi negatif olabilir. ⓘ

Tahmin

Viskozite sürekli olarak sıcaklık ve basınca bağlı olduğundan, sonlu bir sayı ile tam olarak karakterize edilemez deneysel ölçümler. Deneysel değerler mevcut değilse, tahmini formüller gerekli hale gelir ilgilenilen sıcaklık ve basınçlarda. Bu özellik termofiziksel simülasyonlar için önemlidir, Bir akışkanın sıcaklık ve basıncının uzay ve zamanla sürekli olarak değişebildiği durumlar. Benzer bir durumla karşılaşılır Viskozitenin sürekli olarak bileşen akışkanların konsantrasyon oranlarına bağlı olduğu saf akışkan karışımları için ⓘ

Seyreltik monatomik gazlar ve bunların karışımları gibi en basit akışkanlar için ab initio kuantum mekaniksel hesaplamalar viskoziteyi aşağıdaki terimlerle doğru bir şekilde tahmin edebilir temel atomik sabitlerin, yani mevcut viskozite ölçümlerine atıfta bulunmadan. Seyreltik helyum özel durumu için, Ab initio hesaplanan viskozitedeki belirsizlikler, deneysel değerlerdeki belirsizliklerden iki kat daha küçüktür. ⓘ

Çoğu akışkan için, bu tür yüksek doğruluklu, ilk prensip hesaplamaları mümkün değildir. Bunun yerine, teorik veya ampirik ifadeler mevcut viskozite ölçümlerine uydurulmalıdır. Böyle bir ifade, geniş bir sıcaklık aralığında yüksek doğruluklu verilere uydurulursa ve basınçlar arasında bir korelasyon varsa, buna o akışkan için "referans korelasyon" denir. Referans korelasyonlar aşağıdakiler için yayınlanmıştır Birçok saf sıvı; su, karbondioksit, amonyak, benzen ve ksenon bunlara birkaç örnektir. Bunların çoğu gaz, sıvı ve süperkritik fazları kapsayan sıcaklık ve basınç aralıklarını kapsar. ⓘ

Termofiziksel modelleme yazılımı genellikle kullanıcı tarafından belirlenen sıcaklık ve basınçta viskoziteyi tahmin etmek için referans korelasyonlara dayanır. Bu korelasyonlar tescilli olabilir. Örnekler REFPROP (tescilli) ve CoolProp (açık kaynak). ⓘ

Viskozite, tek tek parçacıkların istatistikleri cinsinden ifade eden formüller kullanılarak da hesaplanabilir yörüngeler. Bu formüller, doğrusal kayma viskozitesi ve geçici zaman korelasyon fonksiyonu için Green-Kubo ilişkilerini içerir Evans ve Morriss tarafından 1988 yılında türetilen ifadeler. Bu ifadelerin avantajı, biçimsel olarak kesin olmaları ve genel sistemler için geçerli olmalarıdır. Dezavantajı ise detaylı bir çalışma gerektirmesidir. parçacık yörüngeleri bilgisi, yalnızca moleküler dinamikler gibi hesaplama açısından pahalı simülasyonlarda mevcuttur. Parçacıklar arası etkileşimler için de doğru bir model gereklidir ve bu da karmaşık moleküller için elde edilmesi zor olabilir. ⓘ

Seçilen maddeler

Queensland Üniversitesi'nin zift damlatma deneyinde, zift 1927'den beri bir huniden yavaşça damlatılmakta ve yaklaşık her on yılda bir damla damlatılmaktadır. Bu şekilde ziftin viskozitesinin suyun yaklaşık 230 milyar (2,3×10¹¹) katı olduğu tespit edilmiştir. ⓘ

Gözlemlenen viskozite değerleri, yaygın maddeler için bile birkaç büyüklük sırasına göre değişir (aşağıdaki büyüklük sırası tablosuna bakın). Örneğin, %70'lik bir sakaroz (şeker) çözeltisinin viskozitesi suyun 400 katından fazladır ve havanın 26000 katıdır. Daha dramatik olarak, ziftin viskozitesinin suyun 230 milyar katı olduğu tahmin edilmektedir. ⓘ

Su

Dinamik viskozite $\mu$ oda sıcaklığında (25 °C) yaklaşık 0,89 mPa-s'dir. Kelvin cinsinden sıcaklığın bir fonksiyonu olarak viskozite, yarı ampirik Vogel-Fulcher-Tammann denklemi kullanılarak tahmin edilebilir:

\mu =A\exp \left({\frac {B}{T-C}}\right)

Burada A = 0.02939 mPa-s, B = 507.88 K ve C = 149.3 K. Viskozitenin deneysel olarak belirlenen değerleri de aşağıdaki tabloda verilmiştir. 20 °C'deki değerler faydalı bir referanstır: burada dinamik viskozite yaklaşık 1 cP ve kinematik viskozite yaklaşık 1 cSt'dir. ⓘ

Suyun viskozitesi
çeşitli sıcaklıklarda ⓘ
Sıcaklık (°C)	Viskozite (mPa-s veya cP)
10	1.3059
20	1.0016
30	0.79722
50	0.54652
70	0.40355
90	0.31417

Hava

Standart atmosferik koşullar altında (25 °C ve 1 bar basınç), havanın dinamik viskozitesi 18,5 μPa-s olup, aynı sıcaklıktaki suyun viskozitesinden yaklaşık 50 kat daha küçüktür. Çok yüksek basınç dışında, havanın viskozitesi çoğunlukla sıcaklığa bağlıdır. Sıcaklık bağımlılığı için birçok olası yaklaşık formül arasında (bkz. Viskozitenin sıcaklığa bağımlılığı), bir tanesi

\eta _{\text{air}}=2.791\cdot 10^{-7}\cdot T^{0.7355}

ⓘ

Bu formül -20 °C ila 400 °C aralığında doğrudur. Bu formülün geçerli olabilmesi için sıcaklık kelvin cinsinden verilmelidir; $\eta _{\text{air}}$ o zaman Pa-s cinsinden viskoziteye karşılık gelir. ⓘ

Çiseleyen bal ⓘ

Diğer yaygın maddeler

Madde	Viskozite (mPa-s)	Sıcaklık (°C)
Benzen	0.604	25
Su	1.0016	20
Merkür	1.526	25
Tam yağlı süt	2.12	20
Koyu bira	2.53	20
Zeytinyağı	56.2	26
Bal	$\approx$ 2000–10000	20
Ketçap	$\approx$ 5000–20000	25
Fıstık ezmesi	$\approx$ 10⁴–10⁶
Saha	2.3×10¹¹	10-30 (değişken)

Büyüklük sırası tahminleri

Aşağıdaki tablo, yaygın maddelerde gözlenen viskozite değerleri aralığını göstermektedir. Aksi belirtilmedikçe, 25 °C sıcaklık ve 1 atmosfer basınç varsayılmıştır. ⓘ

Listelenen değerler, ölçüm belirsizlikleri, malzeme tanımlarındaki değişkenlik veya Newtonyen olmayan davranışları hesaba katmadığından, yalnızca temsili tahminlerdir. ⓘ

Faktör (Pa-s)	Açıklama	Örnekler	Değerler (Pa-s)
10⁻⁶	Düşük gaz viskozite aralığı	Bütan	7.49 × 10⁻⁶
10⁻⁶	Düşük gaz viskozite aralığı	Hidrojen	8.8 × 10⁻⁶
10⁻⁵	Gaz viskozitesinin üst aralığı	Kripton	2.538 × 10⁻⁵
10⁻⁵	Gaz viskozitesinin üst aralığı	Neon	3.175 × 10⁻⁵
10⁻⁴	Düşük sıvı viskozite aralığı	Pentan	2.24 × 10⁻⁴
		Benzin	6 × 10⁻⁴
		Su	8.90 × 10⁻⁴
10⁻³	Küçük moleküller için tipik aralık Newton sıvıları	Etanol	1.074 × 10⁻³
		Merkür	1.526 × 10⁻³
		Tam yağlı süt (20 °C)	2.12 × 10⁻³
		Kan	3 × 10-3 ila 6 × 10-3
		Sıvı çelik (1550 °C)	6 × 10⁻³
10⁻² – 10⁰	Yağlar ve uzun zincirli hidrokarbonlar	Keten tohumu yağı	0.028
		Oleik asit	0.036
		Zeytinyağı	0.084
		SAE 10 Motor yağı	0,085 ila 0,14
		Hint yağı	0.1
		SAE 20 Motor yağı	0,14 ila 0,42
		SAE 30 Motor yağı	0,42 ila 0,65
		SAE 40 Motor yağı	0,65 ila 0,90
		Gliserin	1.5
		Krep şurubu	2.5
10¹ – 10³	Macunlar, jeller ve diğer yarı katılar (genellikle Newtonyen olmayan)	Ketçap	≈ 10¹
		Hardal	≈ 10¹
		Ekşi krema	≈ 10²
		Fıstık ezmesi	≈ 10²
		Domuz yağı	≈ 10³
≈10⁸	Viskoelastik polimerler	Saha	2.3×10⁸
≈10²¹	Belirli katı maddeler viskoelastik Açıklama	Manto (jeoloji)	≈ 10¹⁹ ila 10²⁴

Newton kuramı

Birimler

Akmazlık (dinamik akmazlık): μ

Dinamik akmazlığın SI birimi (Yunan sembol: ${\mu }$ ) pascal-saniye (Pa·s) olup 1 kg·m⁻¹·s⁻¹ ye eşdeğerdir. ⓘ

Dinamik akmazlığın cgs birimi, Jean Louis Marie Poiseuille adına ithafen poise (P) dır. Genellikle yüzde birlik miktarı olan centipoise (cP) kullanılır. Örneğin suyun akmazlığı 20 °C'de 1.0020 cP dir. ⓘ

1 poise = 100 centipoise = 1 g·cm⁻¹·s⁻¹ = 0.1 Pa·s. (Tanımı için bakınız.)9 Haziran 2007 tarihinde Wayback Machine sitesinde arşivlendi.

1 centipoise = 0.001 Pa·s. ⓘ

Kinematik akmazlık: ν = μ/ρ

Kinematik akmazlığın (Yunan sembol: ${\nu }$ ) SI birimi (m²·s⁻¹) dir. Kinematik akmazlığın cgs birimi George Gabriel Stokes'un adına ithafen stokes olup S veya St şeklinde kısaltılır. Bazen centistokes (cS veya cSt) şeklinde de kullanılabilir. = μ/ρ ⓘ

1 stokes = 100 centistokes = 1 cm²·s⁻¹ = 0.0001 m²·s⁻¹. = μ/ρ ⓘ

Kinematik ve dinamik akmazlık arasındaki dönüşüm ise $\nu \rho =\mu$ şeklinde verilir ve eğer $\nu$ = 1 St ise

μ = ν ρ = 0.1 kg·m⁻¹s⁻¹·(ρ/(g/cm³)) = 0.1 poise·(ρ/(g/cm³)). [1]4 Kasım 2015 tarihinde Wayback Machine sitesinde arşivlendi. = μ/ρ ⓘ

Sıvılar

Sıvılarda, moleküller arasındaki ilave kuvvetler önemli hale gelir. Bu durumda yüzey gerilimine ilaveler olacaktır ki olgu bugün dahi tartışmalıdır. Dolayısıyla, sıvılarda:

Viskozite basınçtan bağımsızdır (çok yüksek basınçlar hariç) ve
Viskozite, sıcaklık arttıkça azalır (örneğin, sıcaklık 0 °C den 100 °C çıktığında, suyun viskozitesi 1.79 cP den 0.28 cP ye düşer). ⓘ

Sıvıların dinamik viskozitesi, gazların dinamik viskozitesinden on kat daha büyüktür. ⓘ

Havanın akmazlığı

Havanın viskozitesi sıcaklığa bağımlı olup 15.0 °C'de 1.78 × 10⁻⁵ kg/m.s dir. ⓘ

Akışkanlık

Viskozitenin tersi akışkanlık tır ve genellikle φ (= 1/μ) veya F (= 1/η) ile gösterilir. Birimi poise'ın tersi olup (cm·s·g⁻¹), rhe olarak okunur. Mühendislik uygulamalarında nadiren kullanılır. ⓘ

Viskozite ⓘ
Farklı viskozitelere sahip sıvıların simülasyonu. Soldaki sıvı, sağdaki sıvıdan daha düşük viskoziteye sahiptir.
Ortak semboller	$η$ , $μ$
Türevleri diğer miktarlar	$μ = G - t$