Optik

Optik bir sistem üzerinde çalışan bir araştırmacı ⓘ

Optik, ışığın madde ile etkileşimleri ve onu kullanan veya algılayan aletlerin yapımı da dahil olmak üzere ışığın davranışını ve özelliklerini inceleyen fizik dalıdır. Optik genellikle görünür, ultraviyole ve kızılötesi ışığın davranışını tanımlar. Işık elektromanyetik bir dalga olduğu için, X-ışınları, mikrodalgalar ve radyo dalgaları gibi diğer elektromanyetik radyasyon biçimleri de benzer özellikler gösterir. ⓘ

Optik olayların çoğu ışığın klasik elektromanyetik tanımı kullanılarak açıklanabilir. Bununla birlikte, ışığın tam elektromanyetik açıklamalarının pratikte uygulanması genellikle zordur. Pratik optik genellikle basitleştirilmiş modeller kullanılarak yapılır. Bunlardan en yaygın olanı olan geometrik optik, ışığı düz çizgiler halinde hareket eden ve yüzeylerden geçerken ya da yüzeylerden yansırken bükülen ışınlar topluluğu olarak ele alır. Fiziksel optik, geometrik optikte hesaba katılamayan kırınım ve girişim gibi dalga etkilerini içeren daha kapsamlı bir ışık modelidir. Tarihsel olarak, ışığın ışın temelli modeli ilk olarak geliştirilmiş, bunu ışığın dalga modeli izlemiştir. Elektromanyetik teoride 19. yüzyılda kaydedilen ilerleme, ışık dalgalarının aslında elektromanyetik radyasyon olduğunun keşfedilmesine yol açmıştır. ⓘ

Bazı fenomenler ışığın hem dalga benzeri hem de parçacık benzeri özelliklere sahip olmasına bağlıdır. Bu etkilerin açıklanması kuantum mekaniği gerektirir. Işığın parçacık benzeri özellikleri göz önünde bulundurulduğunda, ışık "foton" adı verilen bir parçacıklar topluluğu olarak modellenir. Kuantum optiği, kuantum mekaniğinin optik sistemlere uygulanmasıyla ilgilenir. ⓘ

Optik bilimi, astronomi, çeşitli mühendislik alanları, fotoğrafçılık ve tıp (özellikle fizyolojik optik olarak adlandırılan oftalmoloji ve optometri) dahil olmak üzere birçok ilgili disiplinle ilgilidir ve bu disiplinlerde çalışılmaktadır. Optiğin pratik uygulamaları aynalar, mercekler, teleskoplar, mikroskoplar, lazerler ve fiber optikler dahil olmak üzere çeşitli teknolojilerde ve günlük nesnelerde bulunur. ⓘ

Optik, ışığın dağılımını da inceler ⓘ

Optik
Işığın doğası
Işık
Işık hızı
Huygens-Fresnel ilkesi
Fermat ilkesi
Optik aygıtlar
Ayna
Mercek
Prizma
Büyüteç
Kamera
Mikroskop
Teleskop
Lazer
Göz
Olaylar
Yansıma
Tam yansıma
Kırılma
Saçılma
Girişim
Kırınım
Polarizasyon

Tarihçe

Nimrud merceği ⓘ

Optik, eski Mısırlılar ve Mezopotamyalılar tarafından merceklerin geliştirilmesiyle başlamıştır. Bilinen en eski mercekler, genellikle kuvars olmak üzere cilalı kristalden yapılmış olup Girit'te MÖ 2000'li yılların başlarına tarihlenmektedir (Heraclion Arkeoloji Müzesi, Yunanistan). Rodos'tan gelen mercekler, Nimrud merceği gibi Asur mercekleri gibi MÖ 700'lere tarihlenmektedir. Antik Romalılar ve Yunanlılar mercek yapmak için cam küreleri suyla doldurmuşlardır. Bu pratik gelişmeleri, antik Yunan ve Hint filozoflarının ışık ve görme teorilerini geliştirmeleri ve Greko-Romen dünyasında geometrik optiğin gelişmesi izlemiştir. Optik kelimesi eski Yunanca'da "görünüş, bakış" anlamına gelen ὀπτική (optikē) kelimesinden gelmektedir. ⓘ

Optik üzerine Yunan felsefesi, görmenin nasıl işlediğine dair iki karşıt teoriye ayrılmıştır: intromisyon teorisi ve emisyon teorisi. İntromisyon yaklaşımı, görmenin nesnelerin göz tarafından yakalanan kendi kopyalarını (eidola olarak adlandırılır) yaymalarından kaynaklandığını düşünüyordu. Demokritos, Epikuros, Aristoteles ve onların takipçileri de dahil olmak üzere pek çok yayıcısı olan bu teori, görmenin gerçekte ne olduğuna dair modern teorilerle bir miktar temas kurmuş gibi görünse de, herhangi bir deneysel temelden yoksun bir spekülasyon olarak kalmıştır. ⓘ

İlk olarak Platon, görsel algının gözler tarafından yayılan ışınlar tarafından gerçekleştirildiği fikri olan emisyon teorisini dile getirmiştir. Ayrıca Timaeus'ta aynaların paritelerinin tersine çevrilmesi hakkında yorum yapmıştır. Yaklaşık yüz yıl sonra Öklid (MÖ 4.-3. yüzyıl) Optik başlıklı bir inceleme yazmış ve görmeyi geometriyle ilişkilendirerek geometrik optiği yaratmıştır. Çalışmasını Platon'un emisyon teorisine dayandırmış, perspektifin matematiksel kurallarını tanımlamış ve kırılmanın etkilerini niteliksel olarak açıklamıştır, ancak gözden çıkan bir ışık demetinin her göz kırpıldığında yıldızları anında aydınlatabileceğini sorgulamıştır. Öklid, ışığın en kısa yörüngesi ilkesini belirtmiş ve düz ve küresel aynalar üzerindeki çoklu yansımaları dikkate almıştır. Batlamyus, Optik adlı eserinde, bir dışavurum-içavurum görme teorisine sahipti: gözden gelen ışınlar (ya da akı) bir koni oluşturuyordu, tepe noktası gözün içindeydi ve tabanı görme alanını tanımlıyordu. Işınlar duyarlıydı ve gözlemcinin aklına yüzeylerin uzaklığı ve yönü hakkında bilgi iletiyordu. Öklid'in büyük bir kısmını özetledi ve kırılma açısını ölçmenin bir yolunu tanımlamaya devam etti, ancak bunun geliş açısı ile arasındaki ampirik ilişkiyi fark edemedi. Plutarkhos (MS 1.-2. yüzyıl) küresel aynalar üzerindeki çoklu yansımaları tanımlamış ve görüntülerin kiralite durumu da dahil olmak üzere hem gerçek hem de hayali büyütülmüş ve küçültülmüş görüntülerin yaratılmasını tartışmıştır. ⓘ

Alhazen (İbn al-Haytham), "Optiğin babası" ⓘ

İbn Sehl'in kırılma yasası hakkındaki bilgisini gösteren el yazmasından bir sayfanın kopyası. ⓘ

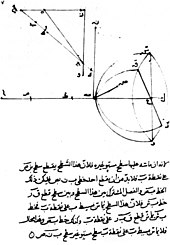
Orta Çağ boyunca, optik hakkındaki Yunan fikirleri Müslüman dünyasındaki yazarlar tarafından yeniden diriltildi ve genişletildi. Bunların en eskilerinden biri, optik fenomenleri daha iyi ölçebildiği için emisyon teorisini tercih ederek, Aristotelesçi ve Öklidçi optik fikirlerinin yararları üzerine yazan Al-Kindi'dir (yaklaşık 801-873). 984 yılında İranlı matematikçi İbn Sahl, Snell yasasına eşdeğer bir kırılma yasasını doğru bir şekilde tanımlayan "Yanan aynalar ve mercekler üzerine" adlı incelemeyi yazdı. Bu yasayı mercekler ve kavisli aynalar için optimum şekilleri hesaplamak için kullandı. 11. yüzyılın başlarında Alhazen (İbn el-Heysem) yansıma ve kırılmayı incelediği Optik Kitabı'nı (Kitab al-manazir) yazdı ve görme ve ışığı gözlem ve deneye dayalı olarak açıklamak için yeni bir sistem önerdi. Batlamyus optiğinin ışınları göz tarafından yayılan "emisyon teorisini" reddetmiş ve bunun yerine ışığın bakılan nesnelerin tüm noktalarından düz çizgiler halinde her yöne yansıdığı ve daha sonra göze girdiği fikrini ortaya atmıştır, ancak gözün ışınları nasıl yakaladığını doğru bir şekilde açıklayamamıştır. Alhazen'in çalışması Arap dünyasında büyük ölçüde göz ardı edildi, ancak M.S. 1200 civarında anonim olarak Latinceye çevrildi ve Polonyalı keşiş Witelo tarafından daha da özetlenip genişletilerek sonraki 400 yıl boyunca Avrupa'da optik üzerine standart bir metin haline getirildi. ⓘ

Ortaçağ Avrupa'sında 13. yüzyılda İngiliz piskopos Robert Grosseteste çok çeşitli bilimsel konularda yazmış ve ışığı dört farklı perspektiften ele almıştır: ışığın epistemolojisi, ışığın metafiziği veya kozmogonisi, ışığın etiyolojisi veya fiziği ve Aristoteles'in eserlerine ve Platonculuğa dayanan bir ışık teolojisi. Grosseteste'in en ünlü öğrencisi Roger Bacon, Alhazen, Aristoteles, İbn-i Sina, İbn-i Rüşd, Öklid, El Kindi, Batlamyus, Tideus ve Afrikalı Konstantin'in eserleri de dahil olmak üzere yakın zamanda tercüme edilen çok çeşitli optik ve felsefi eserlerden alıntı yapan eserler yazdı. Bacon, cam kürelerin parçalarını büyüteç olarak kullanarak ışığın nesnelerden salınmak yerine onlardan yansıdığını göstermeyi başardı. ⓘ

İlk takılabilir gözlükler 1286 civarında İtalya'da icat edildi. Bu, on üçüncü yüzyılda önce Venedik ve Floransa'da, daha sonra da hem Hollanda hem de Almanya'daki gözlük yapım merkezlerinde bu "gözlükler" için mercekleri taşlama ve parlatma optik endüstrisinin başlangıcıydı. Gözlük yapımcıları, günün ilkel optik teorisini (çoğu zaman gözlüklerin nasıl çalıştığını bile yeterince açıklayamayan teori) kullanmaktan ziyade, merceklerin etkilerini gözlemleyerek elde ettikleri ampirik bilgilere dayanarak görmenin düzeltilmesi için geliştirilmiş mercek türleri yarattılar. Merceklerle ilgili bu pratik gelişim, ustalık ve deneyler doğrudan 1595 civarında bileşik optik mikroskobun ve 1608'de her ikisi de Hollanda'daki gözlük yapım merkezlerinde ortaya çıkan kırılan teleskobun icadına yol açtı. ⓘ

Johannes Kepler'in optik hakkındaki ilk incelemesi, Ad Vitellionem paralipomena quibus astronomiae pars optica traditur (1604) ⓘ

17. yüzyılın başlarında Johannes Kepler yazılarında geometrik optiği genişleterek mercekleri, düz ve kavisli aynalarla yansımayı, iğne deliği kameralarının prensiplerini, ışığın yoğunluğunu yöneten ters-kare yasasını ve ay ve güneş tutulmaları ile astronomik paralaks gibi astronomik olayların optik açıklamalarını ele aldı. Ayrıca retinanın görüntüleri kaydeden asıl organ olarak rolünü doğru bir şekilde tespit edebilmiş ve nihayet gözlük üreticilerinin önceki 300 yıl boyunca gözlemlediği farklı mercek türlerinin etkilerini bilimsel olarak ölçebilmiştir. Teleskopun icadından sonra Kepler, teleskopların nasıl çalıştığına dair teorik temelleri ortaya koymuş ve daha yüksek büyütme elde etmek için iki dışbükey mercek kullanan Keplerian teleskopu olarak bilinen geliştirilmiş bir versiyonu tanımlamıştır. ⓘ

Newton'un Opticks kitabının ilk baskısının kapağı (1704) ⓘ

Optik teori, 17. yüzyılın ortalarında filozof René Descartes tarafından yazılan ve ışığın onu üreten nesneler tarafından yayıldığını varsayarak yansıma ve kırılma dahil olmak üzere çeşitli optik fenomenleri açıklayan incelemelerle ilerlemiştir. Bu, antik Yunan emisyon teorisinden önemli ölçüde farklıydı. 1660'ların sonu ve 1670'lerin başında Isaac Newton, Descartes'ın fikirlerini bir ışık teorisi olarak genişletti ve beyaz ışığın bir prizma ile bileşenlerine ayrılabilen renklerin bir karışımı olduğunu tespit etti. 1690 yılında Christiaan Huygens, 1664 yılında Robert Hooke tarafından yapılan önerilere dayanarak ışık için bir dalga teorisi önerdi. Hooke'un kendisi Newton'un ışık teorilerini açıkça eleştirdi ve ikisi arasındaki çekişme Hooke'un ölümüne kadar sürdü. Newton 1704'te Opticks'i yayınladı ve o dönemde, kısmen fiziğin diğer alanlarındaki başarısı nedeniyle, ışığın doğasına ilişkin tartışmada genellikle galip olarak kabul edildi. ⓘ

Newton optiği, Thomas Young ve Augustin-Jean Fresnel'in ışığın dalga doğasını kesin olarak ortaya koyan ışığın girişimi üzerine deneyler yaptığı 19. yüzyılın başlarına kadar genel olarak kabul gördü. Young'ın ünlü çift yarık deneyi, ışığın Newton'un cisim teorisi tarafından öngörülmeyen dalga benzeri bir özellik olan süperpozisyon ilkesini izlediğini gösterdi. Bu çalışma, ışık için bir kırınım teorisine yol açtı ve fiziksel optikte bütün bir çalışma alanı açtı. Dalga optiği, 1860'larda James Clerk Maxwell tarafından elektromanyetik teori ile başarılı bir şekilde birleştirildi. ⓘ

Optik teorisindeki bir sonraki gelişme 1899 yılında Max Planck'ın ışık ve madde arasındaki enerji alışverişinin sadece kuanta adını verdiği ayrık miktarlarda gerçekleştiğini varsayarak kara cisim radyasyonunu doğru bir şekilde modellemesiyle geldi. 1905 yılında Albert Einstein, ışığın kendisinin kuantizasyonunu kesin olarak ortaya koyan fotoelektrik etki teorisini yayınladı. 1913'te Niels Bohr, atomların yalnızca ayrık miktarlarda enerji yayabileceğini gösterdi ve böylece emisyon ve absorpsiyon spektrumlarında görülen ayrık çizgileri açıkladı. Bu gelişmelerin ardından gelen ışık ve madde arasındaki etkileşimin anlaşılması sadece kuantum optiğinin temelini oluşturmakla kalmadı, aynı zamanda bir bütün olarak kuantum mekaniğinin gelişimi için de çok önemliydi. Nihai doruk noktası olan kuantum elektrodinamiği teorisi, tüm optik ve elektromanyetik süreçleri genel olarak gerçek ve sanal fotonların değiş tokuşunun sonucu olarak açıklar. Kuantum optiği, 1953'te maserin ve 1960'ta lazerin icat edilmesiyle pratik önem kazanmıştır. ⓘ

Paul Dirac'ın kuantum alan teorisindeki çalışmalarını takiben George Sudarshan, Roy J. Glauber ve Leonard Mandel, 1950'ler ve 1960'larda kuantum teorisini elektromanyetik alana uygulayarak fotodeteksiyon ve ışık istatistikleri hakkında daha ayrıntılı bir anlayış kazanmışlardır. ⓘ

Klasik optik

Klasik optik iki ana dala ayrılır: geometrik (veya ışın) optik ve fiziksel (veya dalga) optik. Geometrik optikte ışığın düz çizgiler halinde hareket ettiği kabul edilirken, fiziksel optikte ışık elektromanyetik bir dalga olarak kabul edilir. ⓘ

Geometrik optik, kullanılan ışığın dalga boyu modellenen sistemdeki optik elemanların boyutundan çok daha küçük olduğunda geçerli olan fiziksel optiğin bir yaklaşımı olarak görülebilir. ⓘ

Geometrik optik

Işık ışınlarının yansıma ve kırılma geometrisi

Geometrik optik veya ışın optiği, ışığın yayılmasını düz çizgiler halinde hareket eden ve yolları farklı ortamlar arasındaki arayüzlerde yansıma ve kırılma yasaları tarafından yönetilen "ışınlar" açısından tanımlar. Bu yasalar MS 984 yılına kadar deneysel olarak keşfedilmiş ve o zamandan günümüze kadar optik bileşenlerin ve aletlerin tasarımında kullanılmıştır. Bunlar aşağıdaki şekilde özetlenebilir:

Bir ışık ışını iki saydam malzeme arasındaki sınıra çarptığında, yansıyan ve kırılan ışın olarak ikiye ayrılır. ⓘ

Yansıma yasası, yansıyan ışının geliş düzleminde yer aldığını ve yansıma açısının geliş açısına eşit olduğunu söyler. ⓘ

Kırılma yasası, kırılan ışının geliş düzleminde yer aldığını ve geliş açısının sinüsünün kırılma açısının sinüsüne bölümünün bir sabit olduğunu söyler:

${\frac {\sin {\theta _{1}}}{\sin {\theta _{2}}}}=n$, ⓘ

Burada n, herhangi iki malzeme ve belirli bir ışık rengi için bir sabittir. Eğer birinci malzeme hava ya da vakum ise, n ikinci malzemenin kırılma indisidir. ⓘ

Yansıma ve kırılma yasaları, bir ışık ışınının iki nokta arasında aldığı yolun en kısa sürede katedilebilecek yol olduğunu belirten Fermat ilkesinden türetilebilir. ⓘ

Yaklaşımlar

Geometrik optik genellikle paraksiyel yaklaşım veya "küçük açı yaklaşımı" yapılarak basitleştirilir. Matematiksel davranış daha sonra doğrusal hale gelir ve optik bileşenlerin ve sistemlerin basit matrislerle tanımlanmasına izin verir. Bu, yaklaşık görüntü ve nesne konumları ve büyütmeler gibi optik sistemlerin temel özelliklerini bulmak için kullanılan Gauss optiği ve paraksiyel ışın izleme tekniklerine yol açar. ⓘ

Yansımalar

Speküler yansıma diyagramı ⓘ

Yansımalar iki türe ayrılabilir: speküler yansıma ve dağınık yansıma. Speküler yansıma, ışığı basit ve öngörülebilir bir şekilde yansıtan aynalar gibi yüzeylerin parlaklığını tanımlar. Bu, uzayda gerçek (reel) veya tahmin edilen (sanal) bir konumla ilişkilendirilebilen yansıyan görüntülerin üretilmesini sağlar. Dağınık yansıma, kağıt veya kaya gibi parlak olmayan malzemeleri tanımlar. Bu yüzeylerden gelen yansımalar sadece istatistiksel olarak tanımlanabilir, yansıyan ışığın tam dağılımı malzemenin mikroskobik yapısına bağlıdır. Birçok dağınık yansıtıcı, herhangi bir açıdan bakıldığında eşit parlaklığa sahip yüzeyleri tanımlayan Lambert'in kosinüs yasası ile tanımlanır veya buna yaklaştırılabilir. Parlak yüzeyler hem speküler hem de difüz yansıma verebilir. ⓘ

Speküler yansımada, yansıyan ışının yönü, gelen ışının, ışının çarptığı noktada yüzeye dik bir çizgi olan yüzey normali ile yaptığı açı ile belirlenir. Gelen ve yansıyan ışınlar ve normal tek bir düzlemde yer alır ve yansıyan ışın ile yüzey normali arasındaki açı, gelen ışın ile normal arasındaki açı ile aynıdır. Bu Yansıma Yasası olarak bilinir. ⓘ

Düz aynalar için yansıma kanunu, nesnelerin görüntülerinin dik ve aynanın arkasında nesnelerin aynanın önünde olduğu kadar aynı mesafede olduğunu ima eder. Görüntü boyutu nesne boyutu ile aynıdır. Yasa aynı zamanda ayna görüntülerinin paritelerinin ters olduğunu ima eder ki biz bunu sol-sağ tersliği olarak algılarız. İki (veya herhangi bir çift sayıda) aynadaki yansımadan oluşan görüntüler ters çevrilmiş değildir. Köşe yansıtıcılar, gelen ışınların geldiği yönde geri giden yansıyan ışınlar üretir. Buna retrorefleksiyon denir. ⓘ

Eğri yüzeyli aynalar, ışın izleme ve yüzeydeki her noktada yansıma kanunu kullanılarak modellenebilir. Parabolik yüzeyli aynalar için, aynaya gelen paralel ışınlar ortak bir odakta birleşen yansıyan ışınlar üretir. Diğer kavisli yüzeyler de ışığı odaklayabilir, ancak odağın uzayda dağılmasına neden olan ıraksak şekilden kaynaklanan sapmalarla birlikte. Özellikle küresel aynalar küresel sapma sergiler. Kavisli aynalar birden büyük veya küçük büyütmeli görüntüler oluşturabilir ve büyütme negatif olabilir, bu da görüntünün ters olduğunu gösterir. Bir aynadaki yansımayla oluşan dik görüntü her zaman sanaldır, ters görüntü ise gerçektir ve bir ekrana yansıtılabilir. ⓘ

Kırılmalar

Hava/su arayüzü gibi n₁ < n₂ durumu için Snell Yasasının gösterimi ⓘ

Kırılma, ışık değişen bir kırılma indisine sahip bir alan boyunca hareket ettiğinde meydana gelir; bu prensip merceklere ve ışığın odaklanmasına izin verir. En basit kırılma durumu, kırılma indisine sahip tekdüze bir ortam arasında bir arayüzey olduğunda meydana gelir $n_{1}$ ve kırılma indisine sahip başka bir ortam $n_{2}$. Bu gibi durumlarda, Snell Yasası ışık ışınında ortaya çıkan sapmayı tanımlar:

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\$ ⓘ

burada $\theta _{1}$ ve $\theta _{2}$ sırasıyla normal (arayüze) ile gelen ve kırılan dalgalar arasındaki açılardır. ⓘ

Bir ortamın kırılma indisi, ışığın o ortamdaki hızı olan v ile şu şekilde ilişkilidir

$n=c/v$,

Burada c ışığın vakumdaki hızıdır. ⓘ

Snell Yasası, kırılma indisleri ve ortamın geometrisi bilindiği sürece ışık ışınlarının doğrusal ortamdan geçerken sapmasını tahmin etmek için kullanılabilir. Örneğin, ışığın bir prizma boyunca yayılması, prizmanın şekline ve yönüne bağlı olarak ışık ışınının sapmasına neden olur. Çoğu malzemede kırılma indisi ışığın frekansına göre değişir. Bunu dikkate alarak Snell Yasası, bir prizmanın ışığı bir spektruma nasıl dağıtacağını tahmin etmek için kullanılabilir. Işığı bir prizmadan geçirirken bu fenomenin keşfi Isaac Newton'a atfedilir. ⓘ

Bazı ortamlar, konumla kademeli olarak değişen bir kırılma indisine sahiptir ve bu nedenle ortamdaki ışık ışınları kavislidir. Bu etki sıcak günlerde görülen seraplardan sorumludur: kırılma indeksinin yükseklikle birlikte değişmesi ışık ışınlarının bükülmesine neden olarak uzaktaki speküler yansımaların görünümünü yaratır (sanki bir su havuzunun yüzeyindeymiş gibi). Değişken kırılma indekslerine sahip optik malzemeler gradyan indeksli (GRIN) malzemeler olarak adlandırılır. Bu tür malzemeler gradyan indeksli optikler yapmak için kullanılır. ⓘ

Yüksek kırılma indisine sahip bir malzemeden düşük kırılma indisine sahip bir malzemeye doğru hareket eden ışık ışınları için Snell yasası $\theta _{2}$ ne zaman $\theta _{1}$ büyüktür. Bu durumda hiçbir iletim gerçekleşmez; tüm ışık yansıtılır. Bu olguya toplam iç yansıma adı verilir ve fiber optik teknolojisine olanak tanır. Işık bir optik fiberden aşağıya doğru ilerlerken, toplam iç yansımaya uğrar ve kablo uzunluğu boyunca esasen hiç ışık kaybı olmaz. ⓘ

Lensler

Yakınsak bir mercek için ışın izleme diyagramı. ⓘ

Kırılma nedeniyle yakınlaşan veya uzaklaşan ışık ışınları üreten bir cihaz mercek olarak bilinir. Mercekler odak uzunlukları ile karakterize edilir: yakınsak bir mercek pozitif odak uzunluğuna sahipken, ıraksak bir mercek negatif odak uzunluğuna sahiptir. Daha küçük odak uzaklığı, merceğin daha güçlü bir yakınlaştırma veya uzaklaştırma etkisine sahip olduğunu gösterir. Basit bir merceğin havadaki odak uzaklığı mercekçi denklemi ile verilir. ⓘ

Işın izleme, görüntülerin bir mercek tarafından nasıl oluşturulduğunu göstermek için kullanılabilir. Havadaki ince bir mercek için görüntünün konumu basit denklemle verilir ⓘ

${\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}}$, ⓘ

burada $S_{1}$ nesneden merceğe olan mesafedir, $S_{2}$ mercekten görüntüye olan mesafedir ve $f$ merceğin odak uzaklığıdır. Burada kullanılan işaret kuralına göre, nesne ve görüntü merceğin karşı tarafındaysa nesne ve görüntü mesafeleri pozitiftir. ⓘ

Gelen paralel ışınlar, yakınsak bir mercek tarafından merceğin uzak tarafında, mercekten bir odak uzaklığındaki bir noktaya odaklanır. Buna merceğin arka odak noktası denir. Sonlu bir mesafedeki bir nesneden gelen ışınlar mercekten odak mesafesinden daha uzağa odaklanır; nesne merceğe ne kadar yakınsa, görüntü mercekten o kadar uzakta olur. ⓘ

Uzaklaşan merceklerde, gelen paralel ışınlar mercekten geçtikten sonra, merceğin bir odak uzaklığı önündeki bir noktadan kaynaklanmış gibi görünecek şekilde ayrılır. Bu, merceğin ön odak noktasıdır. Sonlu bir mesafedeki bir nesneden gelen ışınlar, merceğe odak noktasından daha yakın olan ve merceğin nesne ile aynı tarafında bulunan sanal bir görüntü ile ilişkilendirilir. Nesne merceğe ne kadar yakınsa, sanal görüntü de merceğe o kadar yakın olur. Aynalarda olduğu gibi, tek bir mercek tarafından üretilen dik görüntüler sanal, ters görüntüler ise gerçektir. ⓘ

Mercekler görüntüleri bozan sapmalardan muzdariptir. Monokromatik sapmalar, merceğin geometrisinin her nesne noktasından gelen ışınları görüntü üzerindeki tek bir noktaya mükemmel bir şekilde yönlendirmemesi nedeniyle meydana gelirken, kromatik sapmalar merceğin kırılma indisinin ışığın dalga boyuna göre değişmesi nedeniyle meydana gelir. ⓘ

Odak uzaklığı f olan ince dışbükey bir mercekte siyah harflerin görüntüleri kırmızı ile gösterilmiştir. Seçilen ışınlar E, I ve K harfleri için sırasıyla mavi, yeşil ve turuncu ile gösterilmiştir. E'nin (2f'de) eşit boyutlu, gerçek ve ters bir görüntüye sahip olduğuna; I'nın (f'de) görüntüsünün sonsuzda olduğuna; ve K'nın (f/2'de) çift boyutlu, sanal ve dik bir görüntüye sahip olduğuna dikkat ediniz. ⓘ

Fiziksel optik

Fiziksel optikte ışığın bir dalga olarak yayıldığı kabul edilir. Bu model, geometrik optik tarafından açıklanmayan girişim ve kırınım gibi olguları öngörür. Işık dalgalarının havadaki hızı yaklaşık 3,0×10⁸ m/s'dir (vakumda tam olarak 299.792.458 m/s). Görünür ışık dalgalarının dalga boyu 400 ila 700 nm arasında değişir, ancak "ışık" terimi genellikle kızılötesi (0,7-300 μm) ve ultraviyole radyasyona (10-400 nm) da uygulanır. ⓘ

Dalga modeli, hangi ortamda neyin "dalgalandığına" dair bir açıklama gerektirmeden optik bir sistemin nasıl davranacağına dair tahminlerde bulunmak için kullanılabilir. 19'uncu yüzyılın ortalarına kadar çoğu fizikçi, ışık bozulmasının yayıldığı "eterik" bir ortama inanıyordu. Elektromanyetik dalgaların varlığı 1865 yılında Maxwell'in denklemleri ile öngörülmüştür. Bu dalgalar ışık hızında yayılır ve birbirlerine ve aynı zamanda dalgaların yayılma yönüne dik olan değişken elektrik ve manyetik alanlara sahiptir. Kuantum mekaniksel etkilerin göz önünde bulundurulması gerektiği durumlar haricinde ışık dalgaları artık genel olarak elektromanyetik dalgalar olarak ele alınmaktadır. ⓘ

Fiziksel optik kullanarak optik sistemlerin modellenmesi ve tasarımı

Optik sistemlerin analizi ve tasarımı için birçok basitleştirilmiş yaklaşım mevcuttur. Bunların çoğu, ortogonal elektrik ve manyetik vektörlere sahip bir vektör modeli kullanmak yerine, ışık dalgasının elektrik alanını temsil etmek için tek bir skaler miktar kullanır. Huygens-Fresnel denklemi böyle bir modeldir. Bu denklem 1815 yılında Fresnel tarafından, Huygens'in dalga cephesindeki her noktanın ikincil bir küresel dalga cephesi oluşturduğu hipotezine dayanarak deneysel olarak türetilmiş ve Fresnel bunu dalgaların süperpozisyonu prensibiyle birleştirmiştir. Maxwell denklemleri kullanılarak türetilen Kirchhoff kırınım denklemi, Huygens-Fresnel denklemini daha sağlam bir fiziksel temele oturtmaktadır. Huygens-Fresnel prensibinin uygulama örnekleri kırınım ve Fraunhofer kırınımı makalelerinde bulunabilir. ⓘ

Elektrik ve manyetik özellikleri ışığın malzeme ile etkileşimini etkileyen malzemelerle uğraşırken, ışık dalgasının hem elektrik hem de manyetik alanlarının modellenmesini içeren daha titiz modeller gereklidir. Örneğin, metal bir yüzeyle etkileşime giren bir ışık dalgasının davranışı, dielektrik bir malzeme ile etkileşime girdiğinde olandan oldukça farklıdır. Polarize ışığı modellemek için bir vektör modeli de kullanılmalıdır. ⓘ

Sonlu elemanlar yöntemi, sınır elemanları yöntemi ve iletim hattı matris yöntemi gibi sayısal modelleme teknikleri, analitik olarak çözülemeyen sistemlerde ışığın yayılımını modellemek için kullanılabilir. Bu tür modeller hesaplama açısından zahmetlidir ve normalde yalnızca analitik çözümlerle elde edilebilecek olanın ötesinde doğruluk gerektiren küçük ölçekli problemleri çözmek için kullanılır. ⓘ

Geometrik optikten elde edilen tüm sonuçlar, akustik mühendisliği ve sinyal işlemede kullanılan aynı matematiksel ve analitik tekniklerin çoğunu uygulayan Fourier optik teknikleri kullanılarak geri kazanılabilir. ⓘ

Gauss ışın yayılımı, lazer ışınları gibi tutarlı radyasyonun yayılımı için basit bir paraksiyel fiziksel optik modelidir. Bu teknik, kırınımı kısmen hesaba katarak bir lazer ışınının mesafeyle birlikte genişleme oranının ve ışının odaklanabileceği minimum boyutun doğru hesaplanmasına olanak tanır. Gauss ışın yayılımı böylece geometrik ve fiziksel optik arasındaki boşluğu doldurur. ⓘ

Süperpozisyon ve girişim

Doğrusal olmayan etkilerin yokluğunda, süperpozisyon prensibi, bozucuların basitçe eklenmesi yoluyla etkileşen dalga biçimlerinin şeklini tahmin etmek için kullanılabilir. Ortaya çıkan bir desen üretmek için dalgaların bu etkileşimi genellikle "girişim" olarak adlandırılır ve çeşitli sonuçlara yol açabilir. Aynı dalga boyuna ve frekansa sahip iki dalga aynı fazda ise, hem dalga tepeleri hem de dalga çukurları aynı hizaya gelir. Bu, yapıcı girişim ve dalganın genliğinde bir artışla sonuçlanır; bu da ışık için o konumdaki dalga biçiminin parlaklaşmasıyla ilişkilidir. Alternatif olarak, aynı dalga boyuna ve frekansa sahip iki dalga faz dışıysa, dalga tepeleri dalga çukurlarıyla hizalanır ve bunun tersi de geçerlidir. Bu da yıkıcı girişim ve dalganın genliğinde bir azalma ile sonuçlanır ki bu da ışık için o konumdaki dalga formunun kararması ile ilişkilidir. Bu etkinin bir örneği için aşağıya bakınız. ⓘ

birleşik dalga formu
dalga 1
dalga 2
	Fazda iki dalga	İki dalga 180° dışarı fazın

Yağ veya yakıt döküldüğünde, ince film girişimiyle renkli desenler oluşur. ⓘ

Huygens-Fresnel ilkesi, bir dalga cephesinin her noktasının yeni bir bozulma üretimiyle ilişkili olduğunu belirttiğinden, bir dalga cephesinin farklı konumlarda kendisiyle yapıcı veya yıkıcı bir şekilde etkileşime girmesi, düzenli ve öngörülebilir desenlerde parlak ve karanlık saçaklar üretmesi mümkündür. İnterferometri, genellikle mesafelerin veya açısal çözünürlüklerin kesin olarak belirlenmesinin bir aracı olarak bu desenleri ölçme bilimidir. Michelson interferometresi, ışığın hızını doğru bir şekilde ölçmek için girişim etkilerini kullanan ünlü bir araçtı. ⓘ

İnce filmlerin ve kaplamaların görünümü girişim etkilerinden doğrudan etkilenir. Yansıma önleyici kaplamalar, kapladıkları yüzeylerin yansıtıcılığını azaltmak için yıkıcı girişim kullanır ve parlama ve istenmeyen yansımaları en aza indirmek için kullanılabilir. En basit durum, gelen ışığın dalga boyunun dörtte biri kalınlığında tek bir katmandır. Filmin üstünden yansıyan dalga ile film/malzeme arayüzünden yansıyan dalga tam olarak 180° faz dışıdır ve yıkıcı girişime neden olur. Dalgalar sadece bir dalga boyu için tam olarak faz dışıdır, bu da tipik olarak görünür spektrumun merkezine yakın, yaklaşık 550 nm olarak seçilir. Birden fazla katman kullanan daha karmaşık tasarımlar geniş bir bantta düşük yansıtıcılık veya tek bir dalga boyunda aşırı düşük yansıtıcılık elde edebilir. ⓘ

İnce filmlerdeki yapıcı girişim, kaplamanın tasarımına bağlı olarak dar veya geniş olabilen bir dalga boyu aralığında güçlü bir ışık yansıması yaratabilir. Bu filmler dielektrik aynalar, girişim filtreleri, ısı yansıtıcıları ve renkli televizyon kameralarında renk ayrımı için filtreler yapmak için kullanılır. Bu girişim etkisi aynı zamanda petrol tabakalarında görülen renkli gökkuşağı desenlerine de neden olur. ⓘ

Kırınım ve optik çözünürlük

Mesafe ile ayrılmış iki yarıkta kırınım $d$. Parlak saçaklar, siyah çizgilerin siyah çizgilerle ve beyaz çizgilerin beyaz çizgilerle kesiştiği çizgiler boyunca meydana gelir. Bu saçaklar açı ile ayrılır $\theta$ ve sipariş olarak numaralandırılır $n$. ⓘ

Kırınım, ışık girişiminin en yaygın olarak gözlemlendiği süreçtir. Bu etki ilk olarak 1665 yılında Francesco Maria Grimaldi tarafından tanımlanmış ve terim de Latince diffringere "parçalara ayırmak" kelimesinden türetilmiştir. Aynı yüzyılın ilerleyen dönemlerinde Robert Hooke ve Isaac Newton da Newton'un halkalarında kırınım olarak bilinen fenomeni tanımlamış, James Gregory ise kuş tüylerindeki kırınım desenlerine ilişkin gözlemlerini kaydetmiştir. ⓘ

Huygens-Fresnel prensibine dayanan ilk fiziksel optik kırınım modeli 1803 yılında Thomas Young tarafından yakın aralıklı iki yarığın girişim desenleriyle yaptığı girişim deneylerinde geliştirilmiştir. Young, sonuçlarının ancak iki yarığın cisimcikler yerine iki benzersiz dalga kaynağı olarak hareket etmesi durumunda açıklanabileceğini gösterdi. 1815 ve 1818'de Augustin-Jean Fresnel, dalga girişiminin kırınımı nasıl açıklayabileceğinin matematiğini sağlam bir şekilde kurdu. ⓘ

Kırınımın en basit fiziksel modelleri, belirli bir dalga boyundaki (λ) ışığa bağlı olarak aydınlık ve karanlık saçakların açısal ayrılmasını tanımlayan denklemleri kullanır. Genel olarak denklem şu biçimi alır ⓘ

$m\lambda =d\sin \theta$ ⓘ

burada $d$ iki dalga cephesi kaynağı arasındaki ayrımdır (Young'ın deneylerinde bu iki yarıktır), $\theta$ merkezi saçak ile merkezi saçak arasındaki açısal ayrımdır. $m$merkezi maksimumun olduğu üçüncü dereceden saçak $m=0$. ⓘ

Bu denklem, tek bir aralıktan kırınım, birden fazla yarıktan kırınım veya eşit aralıklarla çok sayıda yarık içeren bir kırınım ızgarasından kırınım gibi çeşitli durumları hesaba katmak için biraz değiştirilir. Daha karmaşık kırınım modelleri Fresnel veya Fraunhofer kırınım matematiği ile çalışmayı gerektirir. ⓘ

X-ışını kırınımı, bir kristaldeki atomların bir angstrom mertebesindeki mesafelerde düzenli aralıklara sahip olduğu gerçeğinden yararlanır. Kırınım desenlerini görmek için, bu aralığa benzer dalga boylarına sahip x-ışınları kristalden geçirilir. Kristaller iki boyutlu ızgaralar yerine üç boyutlu nesneler olduğundan, ilişkili kırınım deseni Bragg yansımasına göre iki yönde değişir ve ilişkili parlak noktalar benzersiz desenlerde meydana gelir ve $d$ atomlar arasındaki aralığın iki katıdır. ⓘ

Kırınım etkileri, bir optik detektörün ayrı ışık kaynaklarını optik olarak çözme yeteneğini sınırlar. Genel olarak, bir açıklıktan geçen ışık kırınıma uğrayacaktır ve oluşturulabilecek en iyi görüntüler (kırınım sınırlı optikte açıklandığı gibi) karanlık boşluklar ile ayrılmış, çevreleyen parlak halkalar ile merkezi bir nokta olarak görünür; bu desen bir Airy deseni ve merkezi parlak lob bir Airy diski olarak bilinir. Böyle bir diskin boyutu şu şekilde verilir ⓘ

$\sin \theta =1.22{\frac {\lambda }{D}}$ ⓘ

Burada θ açısal çözünürlük, λ ışığın dalga boyu ve D lens açıklığının çapıdır. İki noktanın açısal ayrımı Airy diskinin açısal yarıçapından önemli ölçüde küçükse, iki nokta görüntüde çözülemez, ancak açısal ayrımları bundan çok daha büyükse, iki noktanın farklı görüntüleri oluşur ve bu nedenle çözülebilirler. Rayleigh, açısal ayrımı Airy disk yarıçapına eşit olan (ilk boşluğa, yani ışığın görülmediği ilk yere kadar ölçülen) iki noktanın çözülmüş olarak kabul edilebileceğine dair biraz keyfi bir "Rayleigh kriteri" tanımlamıştır. Merceğin çapı veya açıklığı ne kadar büyükse çözünürlüğün de o kadar ince olduğu görülebilir. İnterferometri, son derece geniş taban çizgisi açıklıklarını taklit etme kabiliyetiyle, mümkün olan en yüksek açısal çözünürlüğe izin verir. ⓘ

Astronomik görüntüleme için atmosfer, yıldızların parıldamasına neden olan atmosferik saçılma ve dağılma nedeniyle görünür spektrumda optimum çözünürlüğün elde edilmesini engeller. Astronomlar bu etkiyi astronomik görüş kalitesi olarak adlandırırlar. Görüntülerdeki atmosferik bozulmayı ortadan kaldırmak ve kırınım sınırına yaklaşan sonuçlar elde etmek için uyarlanabilir optik olarak bilinen teknikler kullanılmıştır. ⓘ

Dağılma ve saçılma

Bir prizmadan geçen ışık dağılımının kavramsal animasyonu. Yüksek frekanslı (mavi) ışık en fazla, düşük frekanslı (kırmızı) ışık ise en az saptırılır. ⓘ

Kırılma süreçleri, ışığın dalga boyunun diğer mesafelere benzer olduğu fiziksel optik sınırında, bir tür saçılma olarak gerçekleşir. En basit saçılma türü, elektromanyetik dalgalar tek parçacıklar tarafından saptırıldığında meydana gelen Thomson saçılmasıdır. Işığın dalgasal doğasının belirgin olduğu Thomson saçılması sınırında ışık, frekansa bağlı ve kesinlikle kuantum mekaniksel bir süreç olan ve ışığın parçacık olarak doğasını içeren Compton saçılmasının aksine, frekanstan bağımsız olarak dağılır. İstatistiksel anlamda, ışığın dalga boyundan çok daha küçük çok sayıda parçacık tarafından elastik olarak saçılması Rayleigh saçılması olarak bilinen bir süreçken, dalga boyuna benzer veya daha büyük parçacıklar tarafından saçılma için benzer süreç, yaygın olarak gözlemlenen bir sonuç olan Tyndall etkisi ile Mie saçılması olarak bilinir. Atomlardan veya moleküllerden saçılan ışığın küçük bir kısmı Raman saçılmasına maruz kalabilir, burada atomların ve moleküllerin uyarılması nedeniyle frekans değişir. Brillouin saçılması, ışığın frekansı zamanla yerel değişiklikler ve yoğun bir malzemenin hareketleri nedeniyle değiştiğinde meydana gelir. ⓘ

Dispersiyon, malzeme özelliklerinden (malzeme dispersiyonu) veya bir optik dalga kılavuzunun geometrisinden (dalga kılavuzu dispersiyonu) dolayı farklı ışık frekansları farklı faz hızlarına sahip olduğunda meydana gelir. Dispersiyonun en bilinen şekli, çoğu şeffaf malzemede görülen artan dalga boyu ile kırılma indeksindeki azalmadır. Buna "normal dispersiyon" denir. Tüm dielektrik malzemelerde, malzemenin ışığı absorbe etmediği dalga boyu aralıklarında meydana gelir. Bir ortamın önemli ölçüde emilim yaptığı dalga boyu aralıklarında, kırılma indisi dalga boyu ile artabilir. Buna "anormal dağılım" denir. ⓘ

Renklerin bir prizma tarafından ayrılması normal dağılıma bir örnektir. Prizmanın yüzeylerinde Snell yasası, normale θ açısıyla gelen ışığın arcsin(sin (θ) / n) açısıyla kırılacağını öngörür. Böylece, daha yüksek kırılma indisine sahip olan mavi ışık, kırmızı ışıktan daha güçlü bir şekilde bükülür ve iyi bilinen gökkuşağı deseniyle sonuçlanır. ⓘ

Dağılım: Farklı hızlarda yayılan iki sinüzoid hareketli bir girişim deseni oluşturur. Kırmızı nokta faz hızı ile hareket eder ve yeşil noktalar grup hızı ile yayılır. Bu durumda, faz hızı grup hızının iki katıdır. Kırmızı nokta şeklin solundan sağına doğru hareket ederken iki yeşil noktayı geçer. Gerçekte, (faz hızıyla hareket eden) bireysel dalgalar (grup hızıyla hareket eden) dalga paketinden kaçar. ⓘ

Malzeme dağılımı genellikle Abbe sayısı ile karakterize edilir; bu sayı üç özel dalga boyunda kırılma indisine dayalı basit bir dağılım ölçüsü verir. Dalga kılavuzu dispersiyonu yayılma sabitine bağlıdır. Her iki tür dağılım da dalganın grup özelliklerinde, yani elektromanyetik dalganın genliği ile aynı frekansta değişen dalga paketinin özelliklerinde değişikliklere neden olur. "Grup hızı dispersiyonu" radyasyonun sinyal "zarfının" yayılması olarak ortaya çıkar ve bir grup dispersiyon gecikme parametresi ile ölçülebilir:

$D={\frac {1}{v_{g}^{2}}}{\frac {dv_{g}}{d\lambda }}$ ⓘ

burada $v_{g}$ grup hızıdır. Düzgün bir ortam için grup hızı şöyledir ⓘ

$v_{g}=c\left(n-\lambda {\frac {dn}{d\lambda }}\right)^{-1}$ ⓘ

Burada n kırılma indisi ve c vakumdaki ışık hızıdır. Bu, dağılım gecikme parametresi için daha basit bir form verir:

$D=-{\frac {\lambda }{c}}\,{\frac {d^{2}n}{d\lambda ^{2}}}.$ ⓘ

Eğer D sıfırdan küçükse, ortamın pozitif dağılıma veya normal dağılıma sahip olduğu söylenir. Eğer D sıfırdan büyükse, ortam negatif dağılıma sahiptir. Bir ışık darbesi normal dağılımlı bir ortamdan yayılırsa, sonuç yüksek frekans bileşenlerinin düşük frekans bileşenlerinden daha fazla yavaşlamasıdır. Bu nedenle darbe pozitif kirpikli veya yukarı kirpikli hale gelir ve zamanla frekansı artar. Bu da prizmadan çıkan spektrumun en az kırılan kırmızı ışık ve en çok kırılan mavi/viyole ışık şeklinde görünmesine neden olur. Tersine, bir darbe anormal (negatif) dağıtıcı bir ortamdan geçerse, yüksek frekanslı bileşenler düşük olanlardan daha hızlı hareket eder ve darbe negatif kirpikli veya aşağı kirpikli hale gelir, zamanla frekansı azalır. ⓘ

İster negatif ister pozitif olsun, grup hızı dağılımının sonucu nihayetinde atımın zamansal olarak yayılmasıdır. Bu, optik fiberlere dayalı optik iletişim sistemlerinde dağılım yönetimini son derece önemli hale getirir, çünkü dağılım çok yüksekse, bilgiyi temsil eden bir grup darbenin her biri zaman içinde yayılır ve birleşerek sinyali çıkarmayı imkansız hale getirir. ⓘ

Polarizasyon

Polarizasyon, salınımlarının yönünü tanımlayan dalgaların genel bir özelliğidir. Birçok elektromanyetik dalga gibi enine dalgalar için, dalganın hareket yönüne dik düzlemdeki salınımların yönünü tanımlar. Salınımlar tek bir yönde olabilir (doğrusal polarizasyon) ya da salınım yönü dalga ilerledikçe dönebilir (dairesel ya da eliptik polarizasyon). Dairesel polarize dalgalar hareket yönünde sağa veya sola doğru dönebilir ve bir dalgada bu iki dönüşten hangisinin mevcut olduğuna dalganın kiralitesi denir. ⓘ

Polarizasyonu düşünmenin tipik yolu, elektromanyetik dalga yayılırken elektrik alan vektörünün yönünü takip etmektir. Bir düzlem dalganın elektrik alan vektörü keyfi olarak x ve y olarak etiketlenmiş iki dik bileşene ayrılabilir (z hareket yönünü gösterir). Elektrik alan vektörü tarafından x-y düzleminde izlenen şekil, polarizasyon durumunu tanımlayan bir Lissajous şeklidir. Aşağıdaki şekillerde, elektrik alan vektörünün (mavi) zamanla (dikey eksenler), uzayda belirli bir noktada, x ve y bileşenleri (kırmızı/sol ve yeşil/sağ) ve vektörün düzlemde izlediği yol (mor) ile birlikte evriminin bazı örnekleri gösterilmektedir: Aynı evrim, uzaydaki noktayı yayılmanın tersi yönünde evrimleştirirken belirli bir zamandaki elektrik alanına bakıldığında da meydana gelecektir. ⓘ

Doğrusal

Dairesel

Eliptik polarizasyon ⓘ

Yukarıdaki en soldaki şekilde, ışık dalgasının x ve y bileşenleri aynı fazdadır. Bu durumda, güçlerinin oranı sabittir, dolayısıyla elektrik vektörünün yönü (bu iki bileşenin vektör toplamı) sabittir. Vektörün ucu düzlemde tek bir çizgi izlediğinden, bu özel duruma doğrusal polarizasyon denir. Bu çizginin yönü iki bileşenin göreceli genliklerine bağlıdır. ⓘ

Ortadaki şekilde, iki ortogonal bileşen aynı genliklere sahiptir ve 90° faz dışıdır. Bu durumda, diğer bileşen maksimum veya minimum genlikteyken bir bileşen sıfırdır. Bu gereksinimi karşılayan iki olası faz ilişkisi vardır: x bileşeni y bileşeninden 90° önde olabilir veya y bileşeninden 90° geride olabilir. Bu özel durumda, elektrik vektörü düzlemde bir daire çizer, bu nedenle bu polarizasyona dairesel polarizasyon denir. Daire içindeki dönüş yönü, iki fazlı ilişkilerden hangisinin var olduğuna bağlıdır ve sağ el dairesel polarizasyon ve sol el dairesel polarizasyona karşılık gelir. ⓘ

İki bileşenin aynı genliğe sahip olmadığı ve/veya faz farklarının sıfır ya da 90°'nin katı olmadığı diğer tüm durumlarda polarizasyon eliptik polarizasyon olarak adlandırılır çünkü elektrik vektörü düzlemde bir elips çizer (polarizasyon elipsi). Bu durum yukarıdaki sağdaki şekilde gösterilmektedir. Polarizasyonun detaylı matematiği Jones hesabı kullanılarak yapılır ve Stokes parametreleri ile karakterize edilir. ⓘ

Kutuplaşmanın değiştirilmesi

Farklı polarizasyon modları için farklı kırılma indekslerine sahip ortamlar çift kırılgan olarak adlandırılır. Bu etkinin iyi bilinen tezahürleri optik dalga plakalarında/geciktiricilerde (doğrusal modlar) ve Faraday rotasyonunda/optik rotasyonda (dairesel modlar) görülür. Çift kırılgan ortamdaki yol uzunluğu yeterliyse, düzlem dalgalar kırılma nedeniyle malzemeden önemli ölçüde farklı bir yayılma yönü ile çıkacaktır. Örneğin makroskopik kalsit kristallerinde durum böyledir; bu kristaller izleyiciye, içinden bakılan şeyin iki farklı, ortogonal olarak kutuplaşmış görüntüsünü sunar. Bu etki, 1669 yılında Erasmus Bartholinus tarafından polarizasyonun ilk keşfini sağlamıştır. Buna ek olarak, faz kayması ve dolayısıyla polarizasyon durumundaki değişim genellikle frekansa bağlıdır, bu da dikroizm ile birlikte genellikle parlak renklere ve gökkuşağı benzeri etkilere yol açar. Mineralojide, pleokroizm olarak bilinen bu özelliklerden, polarizasyon mikroskopları kullanılarak minerallerin tanımlanması amacıyla sıklıkla yararlanılır. Buna ek olarak, normalde çift kırılgan olmayan birçok plastik, fotoelastisitenin temelini oluşturan bir olgu olan mekanik strese maruz kaldığında çift kırılgan hale gelecektir. Işık ışınlarının doğrusal polarizasyonunu döndürmek için çift kırılgan olmayan yöntemler arasında, verimli kollineer iletim için tasarlanmış bir prizma setinde toplam iç yansımayı kullanan prizmatik polarizasyon döndürücülerin kullanımı yer alır. ⓘ

Doğrusal olarak kutuplanmış ışığın yönünü değiştiren bir kutuplayıcı.
Bu resimde, θ₁ - θ₀ = θi. ⓘ

Belirli polarizasyon modlarının genliğini azaltan ortamlar dikroik olarak adlandırılır ve bir moddaki radyasyonun neredeyse tamamını bloke eden cihazlar polarize filtreler veya basitçe "polarizörler" olarak bilinir. Adını Étienne-Louis Malus'tan alan Malus yasası, doğrusal polarize bir ışık demetine mükemmel bir polarizör yerleştirildiğinde, içinden geçen ışığın yoğunluğunun, I, şu şekilde verildiğini söyler ⓘ

$I=I_{0}\cos ^{2}\theta _{i}\quad ,$

burada

I₀ başlangıç yoğunluğudur,

ve θ_i ışığın ilk polarizasyon yönü ile polarizörün ekseni arasındaki açıdır. ⓘ

Polarize edilmemiş bir ışık demeti, mümkün olan tüm açılarda doğrusal polarizasyonların düzgün bir karışımını içeriyor gibi düşünülebilir. 'nin ortalama değerinden beri $\cos ^{2}\theta$ 1/2 ise, iletim katsayısı şu hale gelir ⓘ

${\frac {I}{I_{0}}}={\frac {1}{2}}\quad$ ⓘ

Pratikte, polarizörde bir miktar ışık kaybolur ve polarize olmamış ışığın gerçek iletimi bundan biraz daha düşük olacaktır, Polaroid tipi polarizörler için yaklaşık %38, ancak bazı çift kırılımlı prizma türleri için oldukça yüksektir (>%49,9). ⓘ

Genişletilmiş ortamdaki çift kırılma ve dikroizme ek olarak, polarizasyon etkileri farklı kırılma indisine sahip iki malzeme arasındaki (yansıtıcı) arayüzde de meydana gelebilir. Bu etkiler Fresnel denklemleri ile ele alınır. Dalganın bir kısmı iletilir ve bir kısmı yansıtılır, oran geliş açısına ve kırılma açısına bağlıdır. Bu şekilde, fiziksel optik Brewster'ın açısını geri kazanır. Işık bir yüzey üzerindeki ince bir filmden yansıdığında, filmin yüzeylerinden gelen yansımalar arasındaki girişim, yansıyan ve iletilen ışıkta polarizasyon üretebilir. ⓘ

Doğal ışık

Polarize filtrenin bir fotoğrafta gökyüzü üzerindeki etkileri. Soldaki resim polarize filtre olmadan çekilmiştir. Sağdaki resim için filtre, gökyüzünden saçılan mavi ışığın belirli polarizasyonlarını ortadan kaldıracak şekilde ayarlanmıştır. ⓘ

Çoğu elektromanyetik radyasyon kaynağı, ışık yayan çok sayıda atom veya molekül içerir. Bu yayıcılar tarafından üretilen elektrik alanlarının yönü birbiriyle ilişkili olmayabilir, bu durumda ışığın polarize olmadığı söylenir. Eğer yayıcılar arasında kısmi bir korelasyon varsa, ışık kısmen polarize olur. Polarizasyon kaynağın spektrumu boyunca tutarlı ise, kısmen polarize ışık tamamen polarize olmayan bir bileşen ile tamamen polarize bir bileşenin süperpozisyonu olarak tanımlanabilir. Bu durumda ışık, polarizasyon derecesi ve polarizasyon elipsinin parametreleri açısından tanımlanabilir. ⓘ

Parlak şeffaf malzemelerden yansıyan ışık, ışığın yüzeye normal (dik) olduğu durumlar haricinde, kısmen veya tamamen polarize olur. Matematikçi Étienne-Louis Malus'un polarize ışık için ilk matematiksel modelleri geliştirmesini sağlayan ölçümleri yapmasını sağlayan şey bu etkiydi. Polarizasyon, ışık atmosferde saçıldığında meydana gelir. Saçılan ışık, açık gökyüzündeki parlaklığı ve rengi üretir. Saçılan ışığın bu kısmi polarizasyonundan, fotoğraflarda gökyüzünü koyulaştırmak için polarize filtreler kullanılarak yararlanılabilir. Optik polarizasyon esas olarak optik olarak aktif (kiral) moleküller tarafından sergilenen dairesel dikroizm ve optik rotasyon ("dairesel çift kırılma") nedeniyle kimyada önemlidir. ⓘ

Modern optik

Modern optik, 20. yüzyılda popüler hale gelen optik bilimi ve mühendisliği alanlarını kapsar. Optik biliminin bu alanları tipik olarak ışığın elektromanyetik veya kuantum özellikleriyle ilgilidir, ancak diğer konuları da içerir. Modern optiğin önemli bir alt alanı olan kuantum optiği, ışığın özellikle kuantum mekaniksel özellikleriyle ilgilenir. Kuantum optiği sadece teorik değildir; lazerler gibi bazı modern cihazların çalışma prensipleri kuantum mekaniğine bağlıdır. Fotomultiplier ve channeltrons gibi ışık dedektörleri tek tek fotonlara tepki verir. CCD'ler gibi elektronik görüntü sensörleri, bireysel foton olaylarının istatistiklerine karşılık gelen atış gürültüsü sergiler. Işık yayan diyotlar ve fotovoltaik hücreler de kuantum mekaniği olmadan anlaşılamaz. Bu cihazların incelenmesinde kuantum optiği genellikle kuantum elektroniği ile örtüşür. ⓘ

Optik araştırmalarının özel alanları arasında ışığın kristal optik ve metamalzemelerde olduğu gibi belirli malzemelerle nasıl etkileşime girdiğinin incelenmesi yer alır. Diğer araştırmalar, tekil optik, görüntüleme dışı optik, doğrusal olmayan optik, istatistiksel optik ve radyometride olduğu gibi elektromanyetik dalgaların fenomenolojisine odaklanmaktadır. Ayrıca, bilgisayar mühendisleri "yeni nesil" bilgisayarların olası bileşenleri olarak entegre optik, makine görüşü ve fotonik hesaplama konularına ilgi duymaktadır. ⓘ

Günümüzde saf optik bilimi, optik mühendisliği olarak adlandırılan uygulamalı optik bilimlerinden ayırt etmek için optik bilimi veya optik fiziği olarak adlandırılmaktadır. Optik mühendisliğinin öne çıkan alt alanları arasında aydınlatma mühendisliği, fotonik ve optoelektronik ile lens tasarımı, optik bileşenlerin imalatı ve test edilmesi ve görüntü işleme gibi pratik uygulamalar yer almaktadır. Bu alanlardan bazıları, dünyanın farklı bölgelerinde ve endüstrinin farklı alanlarında biraz farklı anlamlara gelen konu terimleri arasındaki belirsiz sınırlarla örtüşmektedir. Doğrusal olmayan optik alanında çalışan araştırmacılardan oluşan profesyonel bir topluluk, lazer teknolojisindeki ilerlemeler sayesinde son birkaç on yılda gelişmiştir. ⓘ

Lazerler

Yüksek güçlü lazerlerle yapılan bunun gibi deneyler modern optik araştırmalarının bir parçasıdır. ⓘ

Lazer, uyarılmış emisyon adı verilen bir süreçle bir tür elektromanyetik radyasyon olan ışığı yayan bir cihazdır. Lazer terimi, Uyarılmış Radyasyon Emisyonu ile Işık Amplifikasyonunun kısaltmasıdır. Lazer ışığı genellikle uzaysal olarak uyumludur, yani ışık ya dar, düşük sapmalı bir ışın halinde yayılır ya da lensler gibi optik bileşenler yardımıyla bir ışına dönüştürülebilir. Lazerin mikrodalga eşdeğeri olan maser ilk olarak geliştirildiğinden, mikrodalga ve radyo frekansları yayan cihazlar genellikle maser olarak adlandırılır. ⓘ

VLT'nin lazer kılavuz yıldızı ⓘ

İlk çalışan lazer 16 Mayıs 1960 tarihinde Theodore Maiman tarafından Hughes Araştırma Laboratuarlarında gösterilmiştir. İlk icat edildiklerinde "sorun arayan bir çözüm" olarak adlandırıldılar. O zamandan bu yana lazerler milyarlarca dolarlık bir endüstri haline geldi ve binlerce çok çeşitli uygulamada kullanım alanı buldu. Lazerlerin genel nüfusun günlük yaşamında görülebilen ilk uygulaması 1974 yılında tanıtılan süpermarket barkod tarayıcısıydı. Lazer içeren ilk başarılı tüketici ürünü 1978'de piyasaya sürülen lazer disk oynatıcıydı, ancak kompakt disk oynatıcı 1982'den itibaren tüketicilerin evlerinde gerçek anlamda yaygınlaşan ilk lazer donanımlı cihaz oldu. Bu optik depolama cihazları, veri almak amacıyla diskin yüzeyini taramak için milimetreden daha küçük bir yarı iletken lazer kullanmaktadır. Fiber-optik iletişim, büyük miktarda bilgiyi ışık hızında iletmek için lazerlere dayanır. Lazerlerin diğer yaygın uygulamaları arasında lazer yazıcılar ve lazer işaretçiler bulunmaktadır. Lazerler tıpta kansız cerrahi, lazerle göz ameliyatı ve lazer yakalama mikrodiseksiyonu gibi alanlarda ve füze savunma sistemleri, elektro-optik karşı önlemler (EOCM) ve lidar gibi askeri uygulamalarda kullanılmaktadır. Lazerler ayrıca hologramlarda, kabarcık programlarında, lazer ışık gösterilerinde ve lazer epilasyonda da kullanılmaktadır. ⓘ

Kapitsa-Dirac etkisi

Kapitsa-Dirac etkisi, duran bir ışık dalgasıyla karşılaşmanın sonucu olarak parçacık demetlerinin kırılmasına neden olur. Işık, çeşitli fenomenler kullanılarak maddeyi konumlandırmak için kullanılabilir (bkz. optik cımbızlar). ⓘ

Uygulamalar

Optik günlük yaşamın bir parçasıdır. Biyolojide görsel sistemlerin yaygınlığı, optiğin beş duyudan birinin bilimi olarak oynadığı merkezi rolü göstermektedir. Pek çok insan gözlük veya kontakt lenslerden faydalanır ve optik, kameralar da dahil olmak üzere pek çok tüketim malının işleyişinin ayrılmaz bir parçasıdır. Gökkuşakları ve seraplar optik olayların örnekleridir. Optik iletişim hem internetin hem de modern telefonun omurgasını oluşturur. ⓘ

İnsan gözü

Bir insan gözü modeli. Bu makalede bahsedilen özellikler şunlardır: 1. vitreus hümör 3. siliyer kas, 6. göz bebeği, 7. ön kamara, 8. kornea, 10. lens korteksi, 22. optik sinir, 26. fovea, 30. retina ⓘ

İnsan gözü, ışığı retina adı verilen ve gözün arka kısmının iç astarını oluşturan bir fotoreseptör hücre tabakasına odaklayarak işlev görür. Odaklanma bir dizi şeffaf ortam tarafından gerçekleştirilir. Göze giren ışık önce gözün optik gücünün çoğunu sağlayan korneadan geçer. Işık daha sonra korneanın hemen arkasındaki sıvıdan (ön kamara) geçerek devam eder ve ardından göz bebeğinden geçer. Işık daha sonra ışığı daha fazla odaklayan ve odağın ayarlanmasını sağlayan mercekten geçer. Işık daha sonra gözdeki ana sıvı kütlesi olan vitröz hümörden geçer ve retinaya ulaşır. Retinadaki hücreler, optik sinirin çıktığı yer hariç, gözün arka tarafını kaplar; bu da kör bir noktaya neden olur. ⓘ

Işığın farklı yönlerine duyarlı olan iki tip fotoreseptör hücresi, çubuklar ve koniler vardır. Çubuk hücreleri geniş bir frekans aralığında ışığın yoğunluğuna duyarlıdır, bu nedenle siyah-beyaz görmeden sorumludur. Çubuk hücreleri, retinanın merkezi görmeden sorumlu bölgesi olan foveada bulunmaz ve ışıktaki uzamsal ve zamansal değişikliklere koni hücreleri kadar duyarlı değildir. Bununla birlikte, retinada koni hücrelerinden yirmi kat daha fazla çubuk hücresi vardır çünkü çubuk hücreleri daha geniş bir alanda bulunur. Daha geniş dağılımları nedeniyle çubuklar çevresel görüşten sorumludur. ⓘ

Buna karşılık, koni hücreleri ışığın genel yoğunluğuna daha az duyarlıdır, ancak farklı frekans aralıklarına duyarlı olan ve bu nedenle renk algısında ve fotopik görmede kullanılan üç çeşidi vardır. Koni hücreleri foveada yoğunlaşmıştır ve yüksek bir görme keskinliğine sahiptir, yani uzaysal çözünürlükte çubuk hücrelerinden daha iyidirler. Koni hücreleri loş ışığa çubuk hücreleri kadar duyarlı olmadığından, gece görüşünün çoğu çubuk hücreleriyle sınırlıdır. Aynı şekilde, koni hücreleri foveada olduğu için, merkezi görme (çoğu okuma, dikiş gibi ince detay işleri veya nesnelerin dikkatli incelenmesi için gereken görme dahil) koni hücreleri tarafından yapılır. ⓘ

Lensin etrafındaki siliyer kaslar gözün odağının ayarlanmasını sağlar. Bu süreç akomodasyon olarak bilinir. Yakın nokta ve uzak nokta, bir nesnenin keskin odak haline getirilebileceği göze en yakın ve en uzak mesafeleri tanımlar. Normal görüşe sahip bir kişi için uzak nokta sonsuzda bulunur. Yakın noktanın konumu, kasların lensin eğriliğini ne kadar artırabildiğine ve lensin yaşla birlikte ne kadar esnek hale geldiğine bağlıdır. Optometristler, oftalmologlar ve gözlükçüler genellikle uygun bir yakın noktanın normal okuma mesafesinden daha yakın olduğunu düşünürler - yaklaşık 25 cm. ⓘ

Görme kusurları optik prensipler kullanılarak açıklanabilir. İnsanlar yaşlandıkça lens daha az esnek hale gelir ve presbiyopi olarak bilinen bir durum olan yakın nokta gözden uzaklaşır. Benzer şekilde, hipermetropiden muzdarip insanlar lenslerinin odak uzunluğunu yakındaki nesnelerin retinalarında görüntülenmesine izin verecek kadar azaltamazlar. Tersine, lenslerinin odak uzunluğunu uzaktaki nesnelerin retinada görüntülenmesine izin verecek kadar artıramayan kişiler miyopluktan muzdariptir ve sonsuzdan çok daha yakın bir uzak noktaya sahiptir. Astigmatizm olarak bilinen bir durum, kornea küresel olmadığında, bunun yerine bir yönde daha kavisli olduğunda ortaya çıkar. Bu durum, yatay olarak uzatılmış nesnelerin retinanın dikey olarak uzatılmış nesnelerden farklı kısımlarına odaklanmasına ve görüntülerin bozulmasına neden olur. ⓘ

Tüm bu durumlar düzeltici lensler kullanılarak düzeltilebilir. Presbiyopi ve hipermetropi için yakınsak bir mercek yakın noktayı göze yaklaştırmak için gerekli ekstra eğriliği sağlarken, miyopi için ıraksak bir mercek uzak noktayı sonsuza göndermek için gerekli eğriliği sağlar. Astigmatizm, bir yönde diğerine göre daha güçlü kavis yapan silindirik yüzeyli bir lensle düzeltilir ve korneanın homojen olmamasını telafi eder. ⓘ

Düzeltici lenslerin optik gücü, metre cinsinden ölçülen odak uzaklığının tersine eşit bir değer olan diyoptri cinsinden ölçülür; pozitif odak uzaklığı yakınsak bir lense, negatif odak uzaklığı ise ıraksak bir lense karşılık gelir. Astigmatizmayı da düzelten lensler için üç sayı verilir: biri küresel güç için, biri silindirik güç için ve biri de astigmatizmanın yönelim açısı için. ⓘ

Görsel efektler

Ponzo İllüzyonu, paralel çizgilerin sonsuza yaklaştıkça birleşiyor gibi görünmesi gerçeğine dayanır. ⓘ

Optik illüzyonlar (görsel illüzyonlar olarak da adlandırılır), nesnel gerçeklikten farklı görsel olarak algılanan görüntülerle karakterize edilir. Göz tarafından toplanan bilgiler beyinde işlenerek görüntülenen nesneden farklı bir algı ortaya çıkar. Optik illüzyonlar, kendilerini oluşturan nesnelerden farklı görüntüler yaratan fiziksel etkiler, aşırı uyarımın (örneğin parlaklık, eğim, renk, hareket) gözler ve beyin üzerindeki fizyolojik etkileri ve göz ve beynin bilinçsiz çıkarımlar yaptığı bilişsel illüzyonlar dahil olmak üzere çeşitli olayların sonucu olabilir. ⓘ

Bilişsel yanılsamalar, belirli optik ilkelerin bilinçsizce yanlış uygulanmasından kaynaklananları içerir. Örneğin, Ames odası, Hering, Müller-Lyer, Orbison, Ponzo, Sander ve Wundt illüzyonlarının tümü, paralel ışık ışınlarının (veya aslında herhangi bir paralel çizgi kümesinin) sanatsal perspektifle iki boyutlu olarak işlenmiş görüntülerde sonsuzda bir ufuk noktasında birleşiyor gibi görünmesi gibi, yakınlaşan ve uzaklaşan çizgiler kullanarak mesafe görünümü önerisine dayanır. Bu öneri aynı zamanda, esasen aynı açısal boyuta sahip olmasına rağmen ayın ufuk çizgisinin yakınında zirvedekinden çok daha büyük göründüğü ünlü ay yanılsamasından da sorumludur. Bu yanılsama Batlamyus'u o kadar şaşırtmıştır ki, Optik adlı eserinde bu yanılsamayı tanımlarken yanlışlıkla atmosferik kırılmaya atfetmiştir. ⓘ

Bir başka optik yanılsama türü de, zihni mevcut olmayan simetrileri ya da asimetrileri algılaması için kandırmak amacıyla kırık desenlerden yararlanır. Örnekler arasında kafe duvarı, Ehrenstein, Fraser spirali, Poggendorff ve Zöllner illüzyonları sayılabilir. Bunlarla bağlantılı olan ancak tam olarak yanılsama sayılmayan durumlar ise periyodik yapıların üst üste binmesi sonucu ortaya çıkan örüntülerdir. Örneğin, ızgara yapısına sahip şeffaf dokular moiré desenleri olarak bilinen şekilleri üretirken, paralel opak çizgiler veya eğriler içeren periyodik şeffaf desenlerin üst üste binmesi çizgi moiré desenlerini üretir. ⓘ

Optik aletler

Çeşitli optik aletlerin 1728 Cyclopaedia'sından çizimleri ⓘ

Tek mercekler fotoğraf mercekleri, düzeltici mercekler ve büyüteçler dahil olmak üzere çeşitli uygulamalara sahipken, tek aynalar parabolik reflektörlerde ve dikiz aynalarında kullanılır. Bir dizi ayna, prizma ve merceğin bir araya getirilmesiyle pratik kullanımları olan bileşik optik aletler üretilir. Örneğin bir periskop, engellerin etrafını görmeyi sağlamak için hizalanmış iki düzlem aynadan ibarettir. Bilimdeki en ünlü bileşik optik aletler, her ikisi de 16. yüzyılın sonlarında Hollandalılar tarafından icat edilen mikroskop ve teleskoptur. ⓘ

Mikroskoplar ilk olarak sadece iki mercekle geliştirilmiştir: bir objektif merceği ve bir göz merceği. Objektif lens esasen bir büyüteçtir ve çok küçük bir odak uzaklığı ile tasarlanırken, göz merceği genellikle daha uzun bir odak uzaklığına sahiptir. Bu, yakın nesnelerin büyütülmüş görüntülerini üretme etkisine sahiptir. Enerjinin korunumu ve ışık ışınlarının daha geniş bir yüzey alanına yayılması nedeniyle büyütülmüş görüntüler daha sönük olduğundan, genellikle ek bir aydınlatma kaynağı kullanılır. Bileşik mikroskoplar olarak bilinen modern mikroskoplar, işlevselliği optimize etmek ve görüntü kararlılığını artırmak için içlerinde birçok merceğe (tipik olarak dört) sahiptir. Biraz farklı bir mikroskop çeşidi olan karşılaştırma mikroskobu, insanlar tarafından kullanıldığında üç boyutlu görünen stereoskopik binoküler bir görünüm üretmek için yan yana görüntülere bakar. ⓘ

Kırılan teleskoplar olarak adlandırılan ilk teleskoplar da tek bir objektif ve göz merceği lensi ile geliştirilmiştir. Mikroskobun aksine, teleskobun objektif lensi optik sapmaları önlemek için büyük bir odak uzaklığı ile tasarlanmıştır. Objektif, çok daha küçük odak uzaklığına sahip bir göz merceğinin odak noktasında olacak şekilde ayarlanan odak noktasında uzaktaki bir nesnenin görüntüsünü odaklar. Bir teleskobun ana hedefi büyütme değil, objektif merceğinin fiziksel boyutuna göre belirlenen ışığın toplanmasıdır. Bu nedenle, teleskoplar normalde göz mercekleri değiştirilerek değiştirilebilen büyütmeden ziyade objektiflerinin çapları ile gösterilir. Bir teleskobun büyütmesi objektifin odak uzunluğunun göz merceğinin odak uzunluğuna bölünmesine eşit olduğundan, daha küçük odak uzunluklu göz mercekleri daha büyük büyütmeye neden olur. ⓘ

Büyük mercekler yapmak büyük aynalar yapmaktan çok daha zor olduğundan, modern teleskopların çoğu yansıtıcı teleskoplardır, yani objektif merceği yerine birincil ayna kullanan teleskoplardır. Kırılan teleskoplar için geçerli olan aynı genel optik hususlar yansıtan teleskoplar için de geçerlidir, yani birincil ayna ne kadar büyük olursa o kadar fazla ışık toplanır ve büyütme yine de birincil aynanın odak uzunluğunun merceğin odak uzunluğuna bölünmesine eşittir. Profesyonel teleskoplarda genellikle göz mercekleri bulunmaz ve bunun yerine odak noktasına bir alet (genellikle şarj bağlı bir cihaz) yerleştirilir. ⓘ

Fotoğrafçılık

Fotoğraf f/32 diyafram açıklığı ile çekilmiştir ⓘ

Fotoğraf f/5 diyafram açıklığı ile çekilmiştir ⓘ

Fotoğrafın optiği hem objektifleri hem de elektromanyetik radyasyonun kaydedildiği ortamı (ister plaka, ister film, isterse de şarj bağlantılı cihaz olsun) içerir. Fotoğrafçılar, kamera ve çekim arasındaki şu ilişki ile özetlenen karşılıklılığı göz önünde bulundurmalıdır ⓘ

Pozlama ∝ DiyaframAlanı × PozlamaZamanı × SahneParlaklık ⓘ

Başka bir deyişle, diyafram açıklığı ne kadar küçükse (daha fazla odak derinliği sağlar), içeri giren ışık o kadar az olur, bu nedenle sürenin artırılması gerekir (hareket meydana gelirse olası bulanıklığa yol açar). Karşılıklılık yasasının kullanımına bir örnek, gün ışığında uygun pozlamayı tahmin etmek için gereken ayarlar için kabaca bir tahmin veren Sunny 16 kuralıdır. ⓘ

Bir fotoğraf makinesinin diyafram açıklığı, f sayısı veya f-stop, f/# adı verilen birimsiz bir sayı ile ölçülür ve genellikle şu şekilde gösterilir $N$ve tarafından verilir

$f/\#=N={\frac {f}{D}}\$

burada $f$ odak uzaklığıdır ve $D$ giriş gözbebeğinin çapıdır. Geleneksel olarak, "f/#" tek bir sembol olarak ele alınır ve f/#'nin belirli değerleri sayı işareti değerle değiştirilerek yazılır. F-durağını artırmanın iki yolu ya giriş gözbebeğinin çapını azaltmak ya da daha uzun bir odak uzaklığına geçmektir (zoom lens durumunda, bu sadece lensi ayarlayarak yapılabilir). Daha yüksek f sayıları, lensin mesafeden bağımsız olarak tüm görüntüleri mükemmel bir şekilde odaklayabilen ancak çok uzun pozlama süreleri gerektiren bir iğne deliği kamerasının sınırına yaklaşması nedeniyle daha büyük bir alan derinliğine sahiptir. ⓘ

Objektifin sağlayacağı görüş alanı objektifin odak uzaklığı ile değişir. Filmin diyagonal boyutu veya kameranın sensör boyutu ile lensin odak uzaklığı arasındaki ilişkiye dayanan üç temel sınıflandırma vardır:

• Normal lens: yaklaşık 50°'lik görüş açısı (bu açı kabaca insan görüşüne eşdeğer kabul edildiği için normal olarak adlandırılır) ve yaklaşık olarak filmin veya sensörün köşegenine eşit bir odak uzaklığı.
• Geniş açılı lens: 60°'den daha geniş görüş açısı ve normal lensten daha kısa odak uzaklığı.
• Uzun odaklı lens: normal bir lensten daha dar görüş açısı. Bu, odak uzaklığı filmin veya sensörün diyagonal ölçüsünden daha uzun olan herhangi bir lenstir. En yaygın uzun odaklı objektif türü, odak uzunluğundan fiziksel olarak daha kısa olması için özel bir telefoto grubu kullanan bir tasarım olan telefoto objektiftir. ⓘ

Modern zoom lensler bu özelliklerin bazılarına veya tümüne sahip olabilir. ⓘ

Gerekli pozlama süresi için mutlak değer, kullanılan ortamın ışığa ne kadar duyarlı olduğuna bağlıdır (film hızı veya dijital ortam için kuantum verimliliği ile ölçülür). İlk fotoğrafçılıkta ışığa duyarlılığı çok düşük olan ortamlar kullanılıyordu ve bu nedenle çok parlak çekimler için bile pozlama sürelerinin uzun olması gerekiyordu. Teknoloji geliştikçe, film kameraları ve dijital kameralar aracılığıyla hassasiyet de artmıştır. ⓘ

Fiziksel ve geometrik optikten elde edilen diğer sonuçlar kamera optiği için de geçerlidir. Örneğin, belirli bir kamera kurulumunun maksimum çözünürlük kapasitesi, gözbebeği boyutuyla ilişkili kırınım sınırı tarafından belirlenir ve kabaca Rayleigh kriteri tarafından verilir. ⓘ

Atmosferik optik

Renkli bir gökyüzü genellikle, Ekim 2007 Kaliforniya orman yangınları sırasında çekilen bu gün batımı fotoğrafında olduğu gibi, ışığın partiküllerden ve kirlilikten saçılmasından kaynaklanır. ⓘ

Atmosferin benzersiz optik özellikleri çok çeşitli muhteşem optik olaylara neden olur. Gökyüzünün mavi rengi, daha yüksek frekanslı (mavi) güneş ışığını gözlemcinin görüş alanına geri yönlendiren Rayleigh saçılmasının doğrudan bir sonucudur. Mavi ışık kırmızı ışıktan daha kolay saçıldığı için, güneş, gün doğumu veya gün batımı sırasında olduğu gibi kalın bir atmosferden gözlemlendiğinde kırmızımsı bir renk alır. Gökyüzündeki ilave partikül maddeler farklı renkleri farklı açılardan saçarak alacakaranlıkta ve şafakta rengarenk parlayan gökyüzü yaratabilir. Atmosferdeki buz kristalleri ve diğer partiküllerin saçılması haleler, artçılar, koronalar, güneş ışığı ışınları ve güneş köpeklerinden sorumludur. Bu tür olaylardaki çeşitlilik, farklı parçacık boyutları ve geometrilerinden kaynaklanmaktadır. ⓘ

Seraplar, havanın kırılma indeksindeki termal değişimler nedeniyle ışık ışınlarının büküldüğü ve uzaktaki nesnelerin yer değiştirmiş veya aşırı derecede bozulmuş görüntülerinin oluştuğu optik fenomenlerdir. Bununla ilişkili diğer dramatik optik fenomenler arasında güneşin tahmin edilenden daha erken ve çarpık bir şekilde doğduğu Novaya Zemlya etkisi de yer almaktadır. Fata Morgana adı verilen ve ufukta, hatta ufkun ötesinde yer alan adalar, kayalıklar, gemiler veya buzdağları gibi nesnelerin "masal şatoları" gibi uzamış ve yükselmiş göründüğü bir sıcaklık terselmesi ile muhteşem bir kırılma şekli meydana gelir. ⓘ

Gökkuşakları, yağmur damlalarındaki iç yansıma ve dağınık ışık kırılmasının bir kombinasyonunun sonucudur. Bir dizi yağmur damlasının arkasından gelen tek bir yansıma, gökyüzünde açısal boyutu 40° ila 42° arasında değişen ve dışı kırmızı olan bir gökkuşağı üretir. Çift gökkuşağı ise iki iç yansımadan meydana gelir ve açısal büyüklüğü 50,5° ila 54° arasında değişir ve dış kısmı mor renktedir. Gökkuşakları güneş gökkuşağının merkezinden 180° uzaktayken görüldüğünden, gökkuşakları güneş ufka yaklaştıkça daha belirgin hale gelir. ⓘ