Logaritma

Logaritma fonksiyonlarının yaygın olarak kullanılan üç tabana göre grafikleri. Özel logb b = 1 noktaları noktalı çizgilerle gösterilir ve tüm eğriler logb 1 = 0'da kesişir. ⓘ

Matematikte logaritma, üs alma işleminin ters fonksiyonudur. Yani, belirli bir x sayısının logaritması, bu x sayısını üretmek için b tabanı olan başka bir sabit sayının yükseltilmesi gereken üssüdür. En basit durumda logaritma, tekrarlanan çarpma işleminde aynı faktörün oluşum sayısını sayar; örneğin 1000 = 10 × 10 × 10 = 10³ olduğundan, 1000'in "10 tabanı logaritması" 3'tür veya log₁₀ (1000) = 3'tür. x'in b tabanına göre logaritması logb (x) veya parantez olmadan logb x, hatta karışıklık mümkün olmadığında veya büyük O gösteriminde olduğu gibi tabanın önemli olmadığı durumlarda açık taban olmadan log x olarak gösterilir. ⓘ

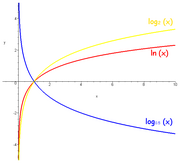
Logaritma tabanı 10 (yani b = 10) ondalık veya ortak logaritma olarak adlandırılır ve bilim ve mühendislikte yaygın olarak kullanılır. Doğal logaritmanın tabanı e sayısıdır (yani b ≈ 2,718); daha basit integrali ve türevi nedeniyle matematik ve fizikte kullanımı yaygındır. İkili logaritma 2 tabanını kullanır (yani b = 2) ve bilgisayar bilimlerinde sıklıkla kullanılır. ⓘ

Logaritma 1614 yılında John Napier tarafından hesaplamaları basitleştirmek için kullanılmaya başlanmıştır. Yüksek doğruluklu hesaplamaları daha kolay gerçekleştirmek için denizciler, bilim insanları, mühendisler, haritacılar ve diğerleri tarafından hızla benimsendi. Logaritma tabloları kullanılarak, sıkıcı çok basamaklı çarpma adımlarının yerini tabloya bakma ve daha basit toplama işlemleri alabilir. Bu, bir çarpımın logaritmasının çarpanların logaritmalarının toplamı olduğu gerçeğinden (kendi başına önemli) dolayı mümkündür:

$\log _{b}(xy)=\log _{b}x+\log _{b}y,$

b, x ve y'nin pozitif olması ve b ≠ 1 olması şartıyla. Yine logaritmaya dayanan sürgülü cetvel, tablolar olmadan hızlı hesaplamalara izin verir, ancak daha düşük hassasiyettedir. Günümüzdeki logaritma kavramı, 18. yüzyılda logaritmayı üstel fonksiyona bağlayan ve aynı zamanda doğal logaritmanın tabanı olarak e harfini kullanan Leonhard Euler'den gelmektedir. ⓘ

Logaritmik ölçekler geniş kapsamlı büyüklükleri daha küçük ölçeklere indirger. Örneğin desibel (dB), çoğunlukla sinyal gücü ve genliği için (ses basıncı yaygın bir örnektir) oranı logaritma olarak ifade etmek için kullanılan bir birimdir. Kimyada pH, sulu bir çözeltinin asitliği için logaritmik bir ölçüdür. Logaritmalar bilimsel formüllerde, algoritmaların ve fraktal adı verilen geometrik nesnelerin karmaşıklık ölçümlerinde yaygın olarak kullanılır. Müzik aralıklarının frekans oranlarını tanımlamaya yardımcı olurlar, asal sayıları sayan veya faktöriyellere yaklaşan formüllerde görünürler, psikofizikteki bazı modelleri bilgilendirirler ve adli muhasebeye yardımcı olabilirler. ⓘ

Üstelleştirmenin tersi olarak logaritma kavramı diğer matematiksel yapılara da uzanır. Bununla birlikte, genel ortamlarda logaritma çok değerli bir fonksiyon olma eğilimindedir. Örneğin, karmaşık logaritma, karmaşık üstel fonksiyonun çok değerli tersidir. Benzer şekilde, ayrık logaritma sonlu gruplarda üstel fonksiyonun çok değerli tersidir; açık anahtar kriptografisinde kullanılır. ⓘ

Logaritmanın bugünkü yazım şekli 18. yüzyıla dayanır. Leonhard Euler logaritmanın üstel işlevlerle olan ilişkisini keşfetmiş ve bugünkü yazımı oluşturmuştur. ⓘ

Motivasyon

Taban 2 logaritmasının grafiği x = 1'de x eksenini keser ve (2, 1), (4, 2) ve (8, 3) noktalarından geçerek örneğin log₂(8) = 3 ve 2³ = 8'i gösterir. Grafik y eksenine keyfi olarak yaklaşır, ancak onu karşılamaz. ⓘ

Toplama, çarpma ve üs alma en temel aritmetik işlemlerden üçüdür. Toplamanın tersi çıkarmadır ve çarpmanın tersi bölmedir. Benzer şekilde logaritma da üs alma işleminin tersidir. Üs alma, taban olan b sayısının üs olan y'nin belirli bir kuvvetine yükseltilerek x değerinin elde edilmesidir; bu işlem şu şekilde gösterilir

$b^{y}=x.$

Örneğin, 2'yi 3'ün kuvvetine yükseltmek 8'i verir: $2^{3}=8$ ⓘ

b tabanının logaritması, x girişinden y çıkışını sağlayan ters işlemdir, $y=\log _{b}x$ ile eşdeğerdir $x=b^{y}$ eğer b pozitif bir reel sayı ise. (Eğer b pozitif bir reel sayı değilse, hem üs alma hem de logaritma tanımlanabilir, ancak tanımları çok daha karmaşık hale getiren çeşitli değerler alabilir). ⓘ

Logaritmayı tanıtmanın ana tarihsel motivasyonlarından biri şu formüldür

$\log _{b}(xy)=\log _{b}x+\log _{b}y,$

(bilgisayarların icadından önce) çarpma ve bölme hesaplamalarını toplama, çıkarma ve logaritma tablosuna bakmaya indirgemeye izin verdi. ⓘ

Tanım

b ≠ 1 olacak şekilde pozitif bir b reel sayısı verildiğinde, pozitif bir x reel sayısının b tabanına göre logaritması, x'i elde etmek için b'nin yükseltilmesi gereken üssüdür. Başka bir deyişle, x'in b tabanına göre logaritması, aşağıdaki gibi tek bir y reel sayısıdır $b^{y}=x$. ⓘ

Logaritma "logb x" olarak gösterilir ("x'in b tabanına göre logaritması", "x'in b tabanına göre logaritması" veya en yaygın olarak "x'in b tabanına göre logu" olarak telaffuz edilir). ⓘ

Eşdeğer ve daha özlü bir tanım, logb fonksiyonunun aşağıdaki fonksiyonun ters fonksiyonu olduğudur $x\mapsto b^{x}$. ⓘ

Örnekler

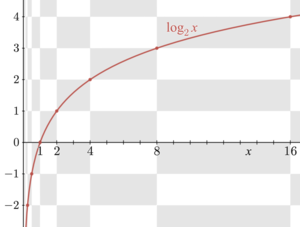
• log₂ 16 = 4, çünkü 2⁴ = 2 × 2 × 2 × 2 = 16.
• Logaritmalar negatif de olabilir: ${\textstyle \log _{2}\!{\frac {1}{2}}=-1}$ çünkü ${\textstyle 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.}$
• log₁₀ 150 yaklaşık olarak 2,176'dır ve 150'nin 102 = 100 ve 103 = 1000 arasında yer alması gibi ² ile ³ arasında yer alır.
• Herhangi bir b tabanı için, sırasıyla b1 = b ve b0 = 1 olduğundan, logb b = ¹ ve logb 1 = ⁰'dır. ⓘ

Logaritmik özdeşlikler

Bazen logaritmik özdeşlikler veya logaritmik yasalar olarak adlandırılan birkaç önemli formül, logaritmaları birbirleriyle ilişkilendirir. ⓘ

Çarpım, bölüm, kuvvet ve kök

Bir çarpımın logaritması, çarpılan sayıların logaritmalarının toplamıdır; iki sayının oranının logaritması, logaritmaların farkıdır. Bir sayının p'inci kuvvetinin logaritması, sayının kendisinin logaritmasının p katıdır; p'inci kökün logaritması, sayının p'ye bölümünün logaritmasıdır. Aşağıdaki tabloda bu özdeşlikler örneklerle listelenmiştir. Özdeşliklerin her biri logaritma tanımlarının değiştirilmesinden sonra türetilebilir $x=b^{\,\log _{b}x}$ veya $y=b^{\,\log _{b}y}$ sol el taraflarında. ⓘ

	Formül	Örnek ⓘ
Ürün	${\textstyle \log _{b}(xy)=\log _{b}x+\log _{b}y}$	${\textstyle \log _{3}243=\log _{3}(9\cdot 27)=\log _{3}9+\log _{3}27=2+3=5}$
Katsayı	${\textstyle \log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y}$	${\textstyle \log _{2}16=\log _{2}\!{\frac {64}{4}}=\log _{2}64-\log _{2}4=6-2=4}$
Güç	${\textstyle \log _{b}\left(x^{p}\right)=p\log _{b}x}$	${\textstyle \log _{2}64=\log _{2}\left(2^{6}\right)=6\log _{2}2=6}$
Kök	${\textstyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}}$	${\textstyle \log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

Taban değişikliği

Logaritma log_b x, aşağıdaki formül kullanılarak keyfi bir k tabanına göre x ve b'nin logaritmalarından hesaplanabilir:

$\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.\,$ ⓘ

Keyfi tabanın logaritmaları arasındaki dönüştürme faktörünün türetilmesi ⓘ

Tanımlayıcı kimlikten başlayarak $x=b^{\log _{b}x}$ Bu denklemin her iki tarafına da logk uygulayarak şunları elde edebiliriz $\log _{k}x=\log _{k}\left(b^{\log _{b}x}\right)=\log _{b}x\cdot \log _{k}b$. için çözme $\log _{b}x$ Verim: $\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}$, verilen dönüşüm faktörünü göstererek $\log _{k}$-değerlerine karşılık gelen $\log _{b}$-olması gereken değerler $(\log _{k}b)^{-1}.$

Tipik bilimsel hesap makineleri 10 ve e tabanlarına göre logaritmaları hesaplar. Herhangi bir b tabanına göre logaritmalar, önceki formülle bu iki logaritmadan biri kullanılarak belirlenebilir:

$\log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.$ ⓘ

Bir x sayısı ve bilinmeyen _bir b tabanına göre logaritması y = logb x verildiğinde, taban şu şekilde verilir:

$b=x^{\frac {1}{y}},$ ⓘ

tanımlayıcı denklemi alarak görülebilir $x=b^{\,\log _{b}x}=b^{y}$ gücüne ${\tfrac {1}{y}}.$ ⓘ

Belirli bazlar

0,5, 2 ve e tabanları için logaritma grafikleri ⓘ

Taban için tüm seçenekler arasında üç tanesi özellikle yaygındır. Bunlar b = 10, b = e (irrasyonel matematik sabiti ≈ 2,71828) ve b = 2'dir (ikili logaritma). Matematiksel analizde, aşağıda açıklanan analitik özellikler nedeniyle e tabanı logaritma yaygındır. Öte yandan, 10 tabanlı logaritmaların ondalık sayı sisteminde manuel hesaplamalar için kullanımı kolaydır:

$\log _{10}(10x)=\log _{10}10+\log _{10}x=1+\log _{10}x.\$

Dolayısıyla, log₁₀ (x) pozitif bir x tamsayısının ondalık basamak sayısı ile ilgilidir: basamak sayısı log₁₀ (x)'ten kesinlikle daha büyük olan en küçük tamsayıdır. Örneğin, log₁₀(1430) yaklaşık olarak 3,15'tir. Bir sonraki tamsayı, 1430'un basamak sayısı olan 4'tür. Hem doğal logaritma hem de iki tabanına göre logaritma bilgi teorisinde kullanılır ve sırasıyla nats veya bitlerin temel bilgi birimleri olarak kullanılmasına karşılık gelir. İkili logaritmalar ayrıca ikili sistemin her yerde bulunduğu bilgisayar biliminde; iki perde oranının (oktav) her yerde bulunduğu ve herhangi iki perde arasındaki sent sayısının oranlarının ikili logaritması, çarpı 1200 olduğu müzik teorisinde de kullanılır (yani, eşit tonlu yarım ton başına 100 sent); ve fotoğrafçılıkta pozlama değerlerini, ışık seviyelerini, pozlama sürelerini, diyafram açıklıklarını ve film hızlarını "durak" cinsinden ölçmek için kullanılır. ⓘ

Aşağıdaki tabloda bu tabanlara göre logaritma için yaygın gösterimler ve kullanıldıkları alanlar listelenmektedir. Birçok disiplin, amaçlanan taban bağlamdan belirlenebildiğinde logb x yerine log x yazar. Blog x gösterimine de rastlanır. "ISO gösterimi" sütununda Uluslararası Standardizasyon Örgütü (ISO 80000-2) tarafından önerilen gösterimler listelenmektedir. log x gösterimi her üç taban için de kullanıldığından (veya taban belirsiz veya önemsiz olduğunda), amaçlanan taban genellikle bağlama veya disipline dayalı olarak çıkarılmalıdır. Bilgisayar bilimlerinde log genellikle log₂ anlamına gelir ve matematikte log genellikle loge anlamına gelir. Diğer bağlamlarda log genellikle log₁₀ anlamına gelir. ⓘ

Taban b	logb x için ad	ISO notasyonu	Diğer notasyonlar	İçinde kullanılır ⓘ
2	ikili logaritma	lb x	ld x, log x, lg x, log2 x	bilgisayar bilimi, bilgi teorisi, biyoinformatik, müzik teorisi, fotoğrafçılık
e	doğal logaritma	ln x	log x (matematikte ve birçok programlama dilinde), loge x	matematik, fizik, kimya, istatistik, ekonomi, bilgi teorisi ve mühendislik
10	ortak logaritma	lg x	log x, log10 x (mühendislik, biyoloji, astronomi alanlarında)	çeşitli mühendislik alanları (bkz. desibel ve aşağıya bakınız), logaritma tabloları, el tipi hesap makineleri, spektroskopi
b	b tabanına göre logaritma	logb x		matemati̇k

Yaygın olarak kullanılan üç tane taban vardır. ⓘ

Tarih

Logaritmanın on yedinci yüzyıl Avrupa'sındaki tarihi, analiz alanını cebirsel yöntemlerin kapsamının ötesine taşıyan yeni bir fonksiyonun keşfidir. Logaritma yöntemi 1614 yılında John Napier tarafından Mirifici Logarithmorum Canonis Descriptio (Logaritmaların Harika Kuralının Açıklaması) başlıklı bir kitapta kamuoyuna açıklanmıştır. Napier'in buluşundan önce, 1600 civarında Jost Bürgi tarafından kapsamlı bir şekilde geliştirilen prosthaphaeresis veya ilerleme tablolarının kullanımı gibi benzer kapsamlarda başka teknikler de vardı. Napier logaritma terimini Orta Latince "logarithmus" teriminden türetmiştir; bu terim Yunanca logos "oran, orantı, kelime" + arithmos "sayı" kelimelerinden türetilmiş olup "oran-sayı" anlamına gelmektedir. ⓘ

Bir sayının genel logaritması, o sayıya eşit olan onluk kuvvetin indeksidir. Bir sayıdan bu kadar çok rakam gerektirecek şekilde bahsetmek, ortak logaritmaya kaba bir göndermedir ve Arşimet tarafından "bir sayının sırası" olarak adlandırılmıştır. İlk gerçek logaritmalar, çarpma işlemini toplama işlemine dönüştüren ve böylece hızlı hesaplamayı kolaylaştıran sezgisel yöntemlerdi. Bu yöntemlerden bazıları trigonometrik özdeşliklerden türetilen tabloları kullanmıştır. Bu tür yöntemlere prosthaphaeresis denir. ⓘ

Günümüzde doğal logaritma olarak bilinen fonksiyonun icadı, Prag'da yaşayan Belçikalı bir Cizvit olan Grégoire de Saint-Vincent tarafından dikdörtgen bir hiperbolün karesini alma girişimi olarak başlamıştır. Arşimet MÖ üçüncü yüzyılda Parabolün Kareselliği'ni yazmıştı, ancak Saint-Vincent 1647'de sonuçlarını yayınlayana kadar hiperbol için bir kareselleştirme tüm çabaları boşa çıkardı. Logaritmanın argümanında geometrik bir ilerleme ile değerlerin aritmetik ilerlemesi arasında sağladığı ilişki, A. A. de Sarasa'yı Saint-Vincent'in karesi ile prosthaphaeresis'teki logaritma geleneği arasında bağlantı kurmaya sevk etti ve doğal logaritma ile eşanlamlı olan "hiperbolik logaritma" terimine yol açtı. Kısa süre sonra yeni fonksiyon Christiaan Huygens ve James Gregory tarafından takdir edildi. Log y gösterimi 1675 yılında Leibniz tarafından benimsendi ve ertesi yıl bunu integral ile ilişkilendirdi ${\textstyle \int {\frac {dy}{y}}.}$ ⓘ

Euler'in modern karmaşık doğal logaritma kavramını geliştirmesinden önce, Roger Cotes 1714 yılında neredeyse eşdeğer bir sonuç elde etmişti

$\log(\cos \theta +i\sin \theta )=i\theta$. ⓘ

Logaritma tabloları, slayt kuralları ve tarihsel uygulamalar

1797 Encyclopædia Britannica logaritma açıklaması ⓘ

Logaritma, hesap makineleri ve bilgisayarlar kullanılmaya başlanmadan önce zor hesaplamaları basitleştirerek bilimin, özellikle de astronominin ilerlemesine katkıda bulunmuştur. Ölçme, göksel navigasyon ve diğer alanlardaki ilerlemeler için kritik öneme sahiptiler. Pierre-Simon Laplace logaritmaları ⓘ

"...[b]irçok ayın emeğini birkaç güne indirerek astronomun ömrünü iki katına çıkaran ve onu uzun hesaplamaların ayrılmaz parçası olan hatalardan ve bıkkınlıktan kurtaran takdire şayan bir marifet." ⓘ

f(x) = bx fonksiyonu logb x'in ters fonksiyonu olduğu için antilogaritma olarak adlandırılmıştır. Günümüzde bu fonksiyon daha yaygın olarak üstel fonksiyon olarak adlandırılmaktadır. ⓘ

Log tabloları

Logaritmanın pratik kullanımını sağlayan önemli bir araç logaritma tablosuydu. Bu türden ilk tablo 1617 yılında Henry Briggs tarafından, Napier'in buluşundan hemen sonra, ancak 10'u taban olarak kullanma yeniliğiyle derlenmiştir. Briggs'in ilk tablosu 1'den 1000'e kadar olan aralıktaki tüm tam sayıların ortak logaritmalarını 14 basamaklı bir hassasiyetle içeriyordu. Daha sonra kapsamı artan tablolar yazıldı. Bu tablolar, belirli bir aralıktaki herhangi bir x sayısı için belirli bir hassasiyette log₁₀ x değerlerini listeliyordu. 10 tabanlı logaritmalar hesaplama için evrensel olarak kullanıldı, bu nedenle ortak logaritma adı verildi, çünkü 10'un faktörlerine göre farklılık gösteren sayıların tam sayılara göre farklılık gösteren logaritmaları vardır. x'in ortak logaritması, karakteristik ve mantissa olarak bilinen bir tamsayı parçasına ve kesirli bir parçaya ayrılabilir. Karakteristik ondalık noktadan itibaren basamakları sayarak kolayca belirlenebildiğinden, logaritma tablolarının yalnızca mantisayı içermesi gerekir. 10 - x'in karakteristiği bir artı x'in karakteristiğidir ve mantisaları aynıdır. Böylece, üç basamaklı bir log tablosu kullanılarak, 3542'nin logaritmasına şu şekilde yaklaşılır ⓘ

$\log _{10}3542=\log _{10}(1000\cdot 3.542)=3+\log _{10}3.542\approx 3+\log _{10}3.54\,$ ⓘ

Enterpolasyon ile daha yüksek doğruluk elde edilebilir:

$\log _{10}3542\approx 3+\log _{10}3.54+0.2(\log _{10}3.55-\log _{10}3.54)\,$ ⓘ

Logaritma monotonik bir fonksiyon olduğundan, 10^x değeri aynı tabloda ters arama ile belirlenebilir. ⓘ

Hesaplamalar

İki pozitif c ve d sayısının çarpımı ve bölümü rutin olarak logaritmalarının toplamı ve farkı olarak hesaplanırdı. Çarpım cd veya bölüm c/d, aynı tablo aracılığıyla toplamın veya farkın antilogaritmasına bakılarak elde edilirdi:

$cd=10^{\,\log _{10}c}\,10^{\,\log _{10}d}=10^{\,\log _{10}c\,+\,\log _{10}d}$

ve

${\frac {c}{d}}=cd^{-1}=10^{\,\log _{10}c\,-\,\log _{10}d}.$ ⓘ

Kayda değer bir hassasiyet gerektiren manuel hesaplamalar için, iki logaritmanın aranması, toplamlarının veya farklarının hesaplanması ve antilogaritmanın aranması, trigonometrik özdeşliklere dayanan prosthaphaeresis gibi önceki yöntemlerle çarpma işlemini gerçekleştirmekten çok daha hızlıdır. ⓘ

Kuvvet ve kök hesaplamaları çarpma veya bölme işlemlerine indirgenir ve

$c^{d}=\left(10^{\,\log _{10}c}\right)^{d}=10^{\,d\log _{10}c}$ ⓘ

ve

${\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.$ ⓘ

Trigonometrik hesaplamalar, trigonometrik fonksiyonların ortak logaritmalarını içeren tablolarla kolaylaştırılmıştır. ⓘ

Slayt kuralları

Bir diğer kritik uygulama ise hesaplama için kullanılan logaritmik olarak bölünmüş bir çift ölçek olan sürgülü cetveldi. Kaymayan logaritmik ölçek, Gunter'in kuralı, Napier'in icadından kısa bir süre sonra icat edildi. William Oughtred bunu geliştirerek birbirine göre hareket edebilen bir çift logaritmik ölçek olan sürgülü cetveli yaratmıştır. Sayılar, logaritmaları arasındaki farklarla orantılı mesafelerde kayan ölçeklere yerleştirilir. Üst ölçeği uygun şekilde kaydırmak, burada gösterildiği gibi logaritmaları mekanik olarak toplamak anlamına gelir:

Bir sürgülü cetvelin şematik gösterimi. Alt ölçekteki 2'den başlayarak, 6 çarpımına ulaşmak için üst ölçekteki 3'e olan mesafeyi ekleyin. Sürgülü cetvel çalışır çünkü 1'den x'e olan mesafe x'in logaritması ile orantılı olacak şekilde işaretlenmiştir. ⓘ

Örneğin, alt ölçekteki 1'den 2'ye olan mesafeyi üst ölçekteki 1'den 3'e olan mesafeye eklediğinizde 6 çarpımı elde edilir ve bu da alt kısımda okunur. Sürgülü cetvel, 1970'lere kadar mühendisler ve bilim insanları için vazgeçilmez bir hesaplama aracıydı, çünkü hassasiyet pahasına, tablolara dayalı tekniklerden çok daha hızlı hesaplamaya izin veriyordu. ⓘ

Analitik özellikler

Logaritma üzerine daha derin bir çalışma, fonksiyon kavramını gerektirir. Fonksiyon, bir sayı verildiğinde başka bir sayı üreten bir kuraldır. Örnek olarak, b tabanının sabit bir sayı olduğu herhangi bir x reel sayısından b'nin x'inci kuvvetini üreten fonksiyon verilebilir. Bu fonksiyon f(x) = b x şeklinde yazılır. b pozitif ve 1'e eşit olmadığında, aşağıda f'nin reellerden pozitif reellere bir fonksiyon olarak düşünüldüğünde ters çevrilebilir olduğunu göstereceğiz. ⓘ

Varoluş

b, 1'e eşit olmayan pozitif bir reel sayı olsun ve f(x) = b x olsun. ⓘ

Reel analizde standart bir sonuçtur ki, herhangi bir sürekli katı monoton fonksiyon, tanım ve aralığı arasında bijective'dir. Bu gerçek, ara değer teoreminden kaynaklanır. Şimdi, f kesinlikle artan (b > 1 için) veya kesinlikle azalan (0 < b < 1 için), sürekli, tanım kümesi $\mathbb {R}$ve menzili vardır $\mathbb {R} _{>0}$. Bu nedenle, f $\mathbb {R}$ için $\mathbb {R} _{>0}$. Başka bir deyişle, her pozitif gerçel y sayısı için tam olarak bir gerçel x sayısı vardır, öyle ki $b^{x}=y$. ⓘ

İzin veriyoruz $\log _{b}\colon \mathbb {R} _{>0}\to \mathbb {R}$ f'nin tersini gösterir. Yani, logb y, aşağıdaki gibi tek bir x reel sayısıdır $b^{x}=y$. Bu fonksiyona b tabanı logaritma fonksiyonu veya logaritmik fonksiyon (veya sadece logaritma) denir. ⓘ

Çarpım formülü ile karakterizasyon

Logb x fonksiyonu da esasen çarpım formülü ile karakterize edilebilir

$\log _{b}(xy)=\log _{b}x+\log _{b}y.$

Daha açık bir ifadeyle, herhangi bir b > 1 tabanına göre logaritma, pozitif reellerden reellere doğru f(b) = 1'i sağlayan tek artan f fonksiyonudur ve

$f(xy)=f(x)+f(y).$ ⓘ

Logaritma fonksiyonunun grafiği

Logaritma fonksiyonunun logb (x) (mavi) grafiği, b^x (kırmızı) fonksiyonunun grafiğinin köşegen çizgisine (x = y) yansıtılmasıyla elde edilir. ⓘ

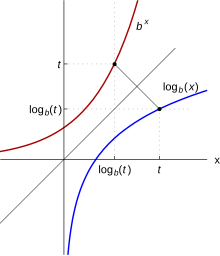
Yukarıda tartışıldığı gibi, log_b fonksiyonu üstel fonksiyonun tersidir $x\mapsto b^{x}$. Bu nedenle, sağda gösterildiği gibi, x ve y koordinatları değiştirildiğinde (veya x = y köşegen çizgisinde yansıtıldığında) grafikleri birbirine karşılık gelir: f grafiğindeki bir nokta (t, u = bt) logaritma grafiğinde bir nokta (u, t = logb u) verir ve bunun tersi de geçerlidir. Sonuç olarak, b'nin birden büyük olması koşuluyla, x sonsuza kadar büyürse logb (x) sonsuza sapar (verilen herhangi bir sayıdan daha büyük olur). Bu durumda, logb(x) artan bir fonksiyondur. b < 1 için, logb (x) bunun yerine eksi sonsuza yönelir. x sıfıra yaklaştığında, logb x b > 1 için eksi sonsuza gider (sırasıyla b < 1 için artı sonsuza). ⓘ

Türev ve antiderivatif

Doğal logaritmanın (yeşil) ve x = 1,5'teki teğetinin (siyah) grafiği ⓘ

Fonksiyonların analitik özellikleri terslerine de geçer. Dolayısıyla, f(x) = bx sürekli ve türevlenebilir bir fonksiyon olduğu için, logb y de öyledir. Kabaca, sürekli bir fonksiyon, grafiğinde keskin "köşeler" yoksa türevlenebilirdir. Dahası, f(x)'in türevi üstel fonksiyonun özelliklerine göre ln(b) bx olarak değerlendirildiğinden, zincir kuralı logb x'in türevinin şu şekilde verildiğini ima eder

${\frac {d}{dx}}\log _{b}x={\frac {1}{x\ln b}}.$

Yani, b tabanı logaritmasının grafiğine (x, logb (x)) noktasında dokunan teğetin eğimi 1/(x ln(b))'ye eşittir. ⓘ

ln(x)'in türevi 1/x'tir; bu da ln(x)'in x = 1 için 0 değerine sahip 1/x'in tek antiderivatifi olduğu anlamına gelir. Doğal logaritmanın "doğal" olarak nitelendirilmesini sağlayan bu çok basit formüldür; bu aynı zamanda e sabitinin öneminin ana nedenlerinden biridir. ⓘ

Genelleştirilmiş fonksiyonel argüman f(x) ile türev şöyledir

${\frac {d}{dx}}\ln f(x)={\frac {f'(x)}{f(x)}}.$

Sağ taraftaki bölüme f'nin logaritmik türevi denir. ln(f(x))'in türevi aracılığıyla f'(x)'in hesaplanması logaritmik türev olarak bilinir. Doğal logaritma ln(x)'in antiderivatifidir:

$\int \ln(x)\,dx=x\ln(x)-x+C.$

Logaritmaların diğer bazlara göre antiderivatifleri gibi ilgili formüller, baz değişimi kullanılarak bu denklemden türetilebilir. ⓘ

Doğal logaritmanın integral gösterimi

t'nin doğal logaritması, f(x) = 1/x (x'in tersi) fonksiyonunun grafiğinin altındaki gölgeli alandır. ⓘ

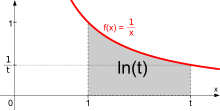
t'nin doğal logaritması belirli integral olarak tanımlanabilir:

$\ln t=\int _{1}^{t}{\frac {1}{x}}\,dx.$

Bu tanımın avantajı, üstel fonksiyona veya herhangi bir trigonometrik fonksiyona dayanmamasıdır; tanım, basit bir karşılıklı integral cinsindendir. Bir integral olarak ln(t), x ekseni ile 1/x fonksiyonunun x = 1 ile x = t arasında değişen grafiği arasındaki alana eşittir. Bu, kalkülüsün temel teoreminin ve ln(x)'in türevinin 1/x olduğu gerçeğinin bir sonucudur. Çarpım ve kuvvet logaritması formülleri bu tanımdan türetilebilir. Örneğin, çarpım formülü ln(tu) = ln(t) + ln(u) olarak çıkarılır:

$\ln(tu)=\int _{1}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(1)}{=}}\int _{1}^{t}{\frac {1}{x}}\,dx+\int _{t}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(2)}{=}}\ln(t)+\int _{1}^{u}{\frac {1}{w}}\,dw=\ln(t)+\ln(u).$ ⓘ

(1) eşitliği integrali iki parçaya bölerken, (2) eşitliği bir değişken değişikliğidir (w = x/t). Aşağıdaki resimde, bölme işlemi alanı sarı ve mavi parçalara ayırmaya karşılık gelmektedir. Sol taraftaki mavi alanı dikey olarak t faktörü ile yeniden ölçeklendirmek ve yatay olarak aynı faktörle küçültmek boyutunu değiştirmez. Uygun şekilde hareket ettirildiğinde, alan yine f(x) = 1/x fonksiyonunun grafiğine uymaktadır. Dolayısıyla, f(x)'in t'den tu'ya integrali olan sol taraftaki mavi alan, 1'den u'ya integral ile aynıdır. Bu da (2) eşitliğini daha geometrik bir kanıtla doğrulamaktadır. ⓘ

Doğal logaritmanın çarpım formülünün görsel bir kanıtı ⓘ

Güç formülü ln(tr) = r ln(t) benzer bir şekilde türetilebilir:

$\ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{w^{r}}}\left(rw^{r-1}\,dw\right)=r\int _{1}^{t}{\frac {1}{w}}\,dw=r\ln(t).$

İkinci eşitlikte değişken değişimi (yerine koyarak integral alma) kullanılır, w = x^1/r. ⓘ

Doğal sayıların karşılıkları üzerinden toplam,

$1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},$

harmonik seri olarak adlandırılır. Doğal logaritma ile yakından ilişkilidir: n sonsuza yaklaştıkça fark artar,

$\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),$

Euler-Mascheroni sabiti γ = 0,5772 olarak bilinen bir sayıya yakınsar (yani keyfi olarak yaklaşır).... Bu ilişki, quicksort gibi algoritmaların performansını analiz etmede yardımcı olur. ⓘ

Logaritmanın aşkınlığı

Cebirsel olmayan reel sayılara transandantal denir; örneğin, π ve e bu tür sayılardır, ancak ${\sqrt {2-{\sqrt {3}}}}$ değildir. Neredeyse tüm gerçek sayılar aşkındır. Logaritma, aşkın bir fonksiyon örneğidir. Gelfond-Schneider teoremi, logaritmaların genellikle transandantal, yani "zor" değerler aldığını ileri sürer. ⓘ

Hesaplama

TI-83 Plus grafik hesap makinesindeki logaritma tuşları (10 tabanı için LOG ve e tabanı için LN) ⓘ

Logaritmaları hesaplamak bazı durumlarda kolaydır, örneğin log₁₀ (1000) = 3. Genel olarak, logaritmalar güç serileri veya aritmetik-geometrik ortalama kullanılarak hesaplanabilir veya sabit bir hassasiyet sağlayan önceden hesaplanmış bir logaritma tablosundan alınabilir. Denklemleri yaklaşık olarak çözmek için yinelemeli bir yöntem olan Newton yöntemi, logaritmayı hesaplamak için de kullanılabilir, çünkü ters fonksiyonu olan üstel fonksiyon verimli bir şekilde hesaplanabilir. Arama tabloları kullanılarak, yalnızca toplama ve bit kaydırma işlemleri kullanılarak logaritma hesaplamak için CORDIC benzeri yöntemler kullanılabilir. Ayrıca, ikili logaritma algoritması, x'in tekrarlanan karelerine dayanarak lb(x)'i özyinelemeli olarak hesaplar ve şu ilişkiden yararlanır

$\log _{2}\left(x^{2}\right)=2\log _{2}|x|.$ ⓘ

Güç serisi

Taylor serisi

z = 1 merkezli ln(z)'nin Taylor serisi. Animasyonda ilk 10 yaklaşımın yanı sıra 99. ve 100. yaklaşımlar da gösterilmektedir. Yaklaşımlar merkezden 1 uzaklığın ötesinde yakınsamamaktadır. ⓘ

0 < z ≤ 2 koşulunu sağlayan herhangi bir gerçek z sayısı için aşağıdaki formül geçerlidir:

${\begin{aligned}\ln(z)&={\frac {(z-1)^{1}}{1}}-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}}-{\frac {(z-1)^{4}}{4}}+\cdots \\&=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {(z-1)^{k}}{k}}\end{aligned}}$

Bu, ln(z)'nin aşağıdaki ifadelerle giderek daha doğru bir değere yaklaştırılabileceğini söylemenin kısaltmasıdır:

${\begin{array}{lllll}(z-1)&&\\(z-1)&-&{\frac {(z-1)^{2}}{2}}&\\(z-1)&-&{\frac {(z-1)^{2}}{2}}&+&{\frac {(z-1)^{3}}{3}}\\\vdots &\end{array}}$

Örneğin, z = 1,5 ile üçüncü yaklaşım 0,4167 değerini verir, bu da ln(1,5) = 0,405465 değerinden yaklaşık 0,011 daha büyüktür. Bu seri, toplam sayısının yeterince büyük olması koşuluyla, ln(z) değerine keyfi bir hassasiyetle yaklaşır. Temel hesapta, ln(z) bu nedenle bu serinin limitidir. Bu, z = 1'deki doğal logaritmanın Taylor serisidir. ln(z)'nin Taylor serisi, z küçük olduğunda, |z| < 1, ln(1 + z) için özellikle yararlı bir yaklaşım sağlar, çünkü o zaman

$\ln(1+z)=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}\cdots \approx z.$

Örneğin, z = 0,1 ile birinci dereceden yaklaşım ln(1,1) ≈ 0,1 değerini verir ki bu da doğru değer olan 0,0953'ün %5'inden daha azdır. ⓘ

Her ne kadar dizi için $\ln(1+z)$ için yakınsar $|z|<1$...düzgün bir numara bunu düzeltebilir. ⓘ

$\ln(1+z)=-\ln \left({\frac {1}{1+z}}\right)=-\ln \left(1-{\frac {z}{z+1}}\right)$ ⓘ

Olarak $\left|{\frac {z}{z+1}}\right|<1$ herkes için $|z|\geq 0$dizisi aynı z aralığı için yakınsar. ⓘ

Ters hiperbolik tanjant

Bir başka seri de ters hiperbolik tanjant fonksiyonuna dayanır:

$\ln(z)=2\cdot \operatorname {artanh} \,{\frac {z-1}{z+1}}=2\left({\frac {z-1}{z+1}}+{\frac {1}{3}}{\left({\frac {z-1}{z+1}}\right)}^{3}+{\frac {1}{5}}{\left({\frac {z-1}{z+1}}\right)}^{5}+\cdots \right),$

Herhangi bir gerçek sayı z > 0 için. Sigma notasyonu kullanılarak bu da şu şekilde yazılır

$\ln(z)=2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {z-1}{z+1}}\right)^{2k+1}.$

Bu seri yukarıdaki Taylor serisinden türetilebilir. Özellikle z 1'e yakınsa, Taylor serisinden daha hızlı yakınsar. Örneğin, z = 1.5 için, ikinci serinin ilk üç terimi yaklaşık 3×10-6 hata ile ln(1.5) değerine yaklaşır. 1'e yakın z için hızlı yakınsamadan şu şekilde yararlanılabilir: düşük doğruluklu bir y ≈ ln(z) yaklaşımı verildiğinde ve

$A={\frac {z}{\exp(y)}},$

z'nin logaritmasıdır:

$\ln(z)=y+\ln(A).$

Başlangıç yaklaşımı y ne kadar iyi olursa, A 1'e o kadar yakın olur, böylece logaritması verimli bir şekilde hesaplanabilir. A, y çok büyük olmadığı sürece hızlı bir şekilde yakınsayan üstel seri kullanılarak hesaplanabilir. Büyük z'nin logaritmasının hesaplanması, z = a - 10b yazılarak z'nin daha küçük değerlerine indirgenebilir, böylece ln(z) = ln(a) + b - ln(10) olur. ⓘ

Tam sayıların logaritmasını hesaplamak için yakından ilişkili bir yöntem kullanılabilir. Koymak $\textstyle z={\frac {n+1}{n}}$ Yukarıdaki seride, şu sonuç çıkar:

$\ln(n+1)=\ln(n)+2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {1}{2n+1}}\right)^{2k+1}.$

Büyük bir n tamsayısının logaritması biliniyorsa, bu seri log(n+1) için hızlı yakınsayan bir seri verir ve yakınsama oranı ${\textstyle \left({\frac {1}{2n+1}}\right)^{2}}$. ⓘ

Aritmetik-geometrik ortalama yaklaşımı

Aritmetik-geometrik ortalama, doğal logaritmanın yüksek hassasiyetli yaklaşımlarını verir. Sasaki ve Kanada 1982'de bunun özellikle 400 ila 1000 ondalık basamak arasındaki hassasiyetler için hızlı olduğunu, Taylor serisi yöntemlerinin ise daha az hassasiyet gerektiğinde tipik olarak daha hızlı olduğunu göstermiştir. Çalışmalarında ln(x), aşağıdaki formülle (Carl Friedrich Gauss'a aittir) 2-p (veya p hassas bit) hassasiyetine yaklaştırılır:

$\ln(x)\approx {\frac {\pi }{2\,\mathrm {M} \!\left(1,2^{2-m}/x\right)}}-m\ln(2).$ ⓘ

Burada M(x, y) x ve y'nin aritmetik-geometrik ortalamasını gösterir. (x + y)/2 (aritmetik ortalama) ortalamasının tekrar tekrar hesaplanmasıyla elde edilir ve ${\textstyle {\sqrt {xy}}}$ (geometrik ortalama) olsun ve bu iki sayı bir sonraki x ve y olsun. İki sayı hızla M(x, y) değeri olan ortak bir limite yakınsar. m öyle seçilir ki ⓘ

$x\,2^{m}>2^{p/2}.\,$ ⓘ

gerekli hassasiyeti sağlamak için. Daha büyük bir m, M(x, y) hesaplamasının daha fazla adım atmasına neden olur (başlangıçtaki x ve y birbirinden daha uzaktır, bu nedenle yakınsama için daha fazla adım gerekir) ancak daha fazla hassasiyet sağlar. π ve ln(2) sabitleri hızlı yakınsayan serilerle hesaplanabilir. ⓘ

Feynman'ın algoritması

Richard Feynman, Los Alamos Ulusal Laboratuvarı'nda Manhattan Projesi üzerinde çalışırken logaritmayı hesaplamak için uzun bölmeye benzeyen ve daha sonra Bağlantı Makinesi'nde kullanılan bir bit işleme algoritması geliştirdi. Algoritma, her 1 < x < 2 gerçek sayısının 1 + 2-k biçimindeki farklı çarpanların bir çarpımı olarak temsil edilebilir olduğu gerçeğini kullanır. Algoritma, P = 1 ve k = 1 ile başlayarak bu P çarpımını sırayla oluşturur: P - (1 + 2-k) < x ise, P'yi P - (1 + 2-k) olarak değiştirir. Daha sonra artar $k$ ne olursa olsun bir. Algoritma, k istenen doğruluğu verecek kadar büyük olduğunda durur. log(x), 1 + 2-k faktörünün P çarpımına dahil edildiği k'lere karşılık gelen log(1 + 2-k) formundaki terimlerin toplamı olduğundan, log(x), tüm k'ler için log(1 + 2-k) tablosu kullanılarak basit bir toplama işlemiyle hesaplanabilir. ⓘ

Uygulamalar

Logaritmik spiral sergileyen bir nautilus ⓘ

Logaritmaların matematik içinde ve dışında birçok uygulaması vardır. Bu uygulamalardan bazıları ölçek değişmezliği kavramıyla ilgilidir. Örneğin, bir nautilus kabuğunun her bir bölmesi, bir sonrakinin sabit bir faktörle ölçeklendirilmiş yaklaşık bir kopyasıdır. Bu da logaritmik bir spiralin ortaya çıkmasına neden olur. Benford'un önde gelen rakamların dağılımına ilişkin yasası da ölçek değişmezliği ile açıklanabilir. Logaritmalar aynı zamanda kendine benzerlikle de bağlantılıdır. Örneğin, logaritmalar bir problemi benzer iki küçük probleme bölerek ve çözümlerini yamalayarak çözen algoritmaların analizinde ortaya çıkar. Kendine benzer geometrik şekillerin, yani parçaları resmin bütününe benzeyen şekillerin boyutları da logaritmalara dayanır. Logaritmik ölçekler, bir değerin mutlak farkının aksine göreceli değişimini ölçmek için kullanışlıdır. Ayrıca, logaritmik fonksiyon log(x) büyük x için çok yavaş büyüdüğünden, logaritmik ölçekler büyük ölçekli bilimsel verileri sıkıştırmak için kullanılır. Logaritmalar ayrıca Tsiolkovsky roket denklemi, Fenske denklemi veya Nernst denklemi gibi çok sayıda bilimsel formülde de yer alır. ⓘ

Logaritmik ölçek

1920'lerdeki Alman hiperenflasyonu sırasında bir Altınmark'ın Papiermark cinsinden değerini gösteren logaritmik bir grafik ⓘ

Bilimsel büyüklükler genellikle logaritmik bir ölçek kullanılarak diğer büyüklüklerin logaritması olarak ifade edilir. Örneğin desibel, logaritmik ölçekli büyüklüklerle ilişkili bir ölçü birimidir. Oranların ortak logaritmasına dayanır - güç oranının ortak logaritmasının 10 katı veya voltaj oranının ortak logaritmasının 20 katı. Elektrik sinyallerinin iletilmesinde voltaj seviyelerindeki kaybı ölçmek, akustikte seslerin güç seviyelerini tanımlamak ve spektrometri ve optik alanlarında ışığın emilimini tanımlamak için kullanılır. (Anlamlı) bir sinyale göre istenmeyen gürültü miktarını tanımlayan sinyal-gürültü oranı da desibel cinsinden ölçülür. Benzer bir şekilde, tepe sinyal-gürültü oranı, logaritma kullanılarak ses ve görüntü sıkıştırma yöntemlerinin kalitesini değerlendirmek için yaygın olarak kullanılır. ⓘ

Bir depremin gücü, depremde yayılan enerjinin ortak logaritması alınarak ölçülür. Bu, moment büyüklüğü ölçeğinde veya Richter büyüklüğü ölçeğinde kullanılır. Örneğin, 5.0'lık bir deprem 4.0'lık bir depremin 32 katı (10^1.5), 6.0'lık bir deprem ise 1000 katı (10³) enerji açığa çıkarır. Görünür büyüklük yıldızların parlaklığını logaritmik olarak ölçer. Kimyada ondalık logaritmanın negatifi olan ondalık kologaritma p harfi ile gösterilir. Örneğin pH, hidronyum iyonlarının aktivitesinin ondalık kologaritmasıdır (hidrojen iyonları H⁺
suda alır). Nötr sudaki hidronyum iyonlarının aktivitesi 10-7 mol-L-1, dolayısıyla pH değeri 7'dir. Sirke tipik olarak yaklaşık 3 pH değerine sahiptir. 4'lük fark, aktivitenin 10⁴'lük bir oranına karşılık gelir, yani sirkenin hidronyum iyonu aktivitesi yaklaşık 10-3 mol-L-1'dir. ⓘ

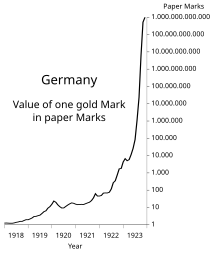
Semilog (log-lineer) grafikler görselleştirme için logaritmik ölçek kavramını kullanır: bir eksen, tipik olarak dikey olan, logaritmik olarak ölçeklendirilir. Örneğin, sağdaki grafik 1 milyondan 1 trilyona olan dik artışı, 1'den 1 milyona olan artışla aynı alana (dikey eksende) sıkıştırmaktadır. Bu tür grafiklerde, f(x) = a - bx biçimindeki üstel fonksiyonlar, eğimi b'nin logaritmasına eşit olan düz çizgiler olarak görünür. Log-log grafikler her iki ekseni de logaritmik olarak ölçeklendirir, bu da f(x) = a - xk biçimindeki fonksiyonların eğimi k üssüne eşit olan düz çizgiler olarak gösterilmesine neden olur. ⓘ

Psikoloji

Logaritma, insan algısını tanımlayan çeşitli yasalarda yer almaktadır: Hick yasası, bireylerin bir alternatifi seçmek için harcadıkları zaman ile sahip oldukları seçenek sayısı arasında logaritmik bir ilişki olduğunu öne sürer. Fitts yasası, bir hedef alana hızla hareket etmek için gereken sürenin, hedefe olan mesafenin ve hedefin büyüklüğünün logaritmik bir fonksiyonu olduğunu öngörür. Psikofizikte Weber-Fechner yasası, bir kişinin taşıdığı bir eşyanın gerçek ve algılanan ağırlığı gibi uyarıcı ve duyum arasında logaritmik bir ilişki önerir. (Ancak bu "yasa", Stevens'ın güç yasası gibi daha yeni modellerden daha az gerçekçidir). ⓘ

Psikolojik çalışmalar, matematik eğitimi az olan bireylerin miktarları logaritmik olarak tahmin etme eğiliminde olduklarını, yani bir sayıyı logaritmasına göre işaretlenmemiş bir çizgi üzerinde konumlandırdıklarını, böylece 10'un 100'e 100'ün 1000'e yakın olduğu kadar yakın konumlandırıldığını ortaya koymuştur. Artan eğitim, bazı durumlarda bunu doğrusal bir tahmine (1000'i 10 kat uzağa konumlandırma) kaydırırken, logaritmalar, çizilecek sayıların doğrusal olarak çizilmesi zor olduğunda kullanılır. ⓘ

Olasılık teorisi ve istatistik

Log-normal dağılıma sahip rastgele değişkenlerin üç olasılık yoğunluk fonksiyonu (PDF). Gösterilen PDF'lerin üçü için de sıfır olan konum parametresi μ, rastgele değişkenin logaritmasının ortalamasıdır, değişkenin kendisinin ortalaması değildir. ⓘ

Dünyanın 237 ülkesinin nüfusundaki ilk rakamların dağılımı (% olarak, kırmızı çubuklar). Siyah noktalar Benford yasası tarafından öngörülen dağılımı göstermektedir. ⓘ

Logaritmalar olasılık teorisinde ortaya çıkar: büyük sayılar yasası, adil bir madeni para için, yazı-tura sayısı sonsuza doğru arttıkça, gözlemlenen tura oranının yarıya yaklaşacağını belirtir. Bu oranın yarıya yakın dalgalanmaları yinelenen logaritma yasası ile tanımlanır. ⓘ

Logaritmalar log-normal dağılımlarda da görülür. Rastgele bir değişkenin logaritması normal bir dağılıma sahip olduğunda, değişkenin log-normal dağılıma sahip olduğu söylenir. Log-normal dağılımlara, bir değişkenin birçok bağımsız pozitif rastgele değişkenin çarpımı olarak oluşturulduğu birçok alanda, örneğin türbülans çalışmalarında rastlanır. ⓘ

Logaritmalar, parametrik istatistiksel modellerin maksimum olabilirlik tahmini için kullanılır. Böyle bir model için olabilirlik fonksiyonu, tahmin edilmesi gereken en az bir parametreye bağlıdır. Olabilirlik fonksiyonunun bir maksimum değeri, olabilirliğin logaritmasının ("log olabilirlik") bir maksimum değeri ile aynı parametre değerinde meydana gelir, çünkü logaritma artan bir fonksiyondur. Log-olabilirliğin maksimize edilmesi, özellikle bağımsız rastgele değişkenler için çarpılmış olabilirlikler için daha kolaydır. ⓘ

Benford yasası, binaların yükseklikleri gibi birçok veri setindeki rakamların oluşumunu açıklar. Benford yasasına göre, veri örneğindeki bir öğenin ilk ondalık basamağının d (1'den 9'a kadar) olma olasılığı, ölçüm birimine bakılmaksızın log₁₀ (d + 1) - log₁₀ (d) değerine eşittir. Dolayısıyla, verilerin yaklaşık %30'unun ilk basamağının 1 olması, %18'inin 2 ile başlaması vb. beklenebilir. Denetçiler, hileli muhasebeyi tespit etmek için Benford yasasından sapmaları inceler. ⓘ

Hesaplama karmaşıklığı

Algoritma analizi, algoritmaların (belirli bir problemi çözen bilgisayar programları) performansını inceleyen bir bilgisayar bilimi dalıdır. Logaritmalar, bir problemi daha küçük problemlere bölen ve alt problemlerin çözümlerini birleştiren algoritmaları tanımlamak için değerlidir. ⓘ

Örneğin, sıralanmış bir listedeki bir sayıyı bulmak için, ikili arama algoritması ortadaki girişi kontrol eder ve sayı hala bulunamazsa ortadaki girişten önceki veya sonraki yarıyla devam eder. Bu algoritma ortalama olarak log₂ (N) karşılaştırma gerektirir, burada N listenin uzunluğudur. Benzer şekilde, birleştirme sıralama algoritması sıralanmamış bir listeyi, listeyi yarıya bölerek ve sonuçları birleştirmeden önce bunları sıralayarak sıralar. Birleştirme sıralama algoritmaları tipik olarak yaklaşık olarak N - log(N) ile orantılı bir zaman gerektirir. Logaritmanın tabanı burada belirtilmez, çünkü başka bir taban kullanıldığında sonuç yalnızca sabit bir faktörle değişir. Standart tekdüze maliyet modeli altındaki algoritmaların analizinde sabit bir faktör genellikle göz ardı edilir. ⓘ

Bir f(x) fonksiyonunun logaritmik olarak büyüdüğü söylenir, eğer f(x) (tam olarak veya yaklaşık olarak) x'in logaritmasıyla orantılıysa. (Bununla birlikte, organizma büyümesinin biyolojik tanımları, bu terimi üstel bir fonksiyon için kullanır). Örneğin, herhangi bir N doğal sayısı log₂ N + 1 bitten daha fazla olmayan ikili formda temsil edilebilir. Başka bir deyişle, N'yi saklamak için gereken bellek miktarı N ile logaritmik olarak büyür. ⓘ

Entropi ve kaos

Oval bir bilardo masası üzerinde bilardo. Merkezde bir derecelik açı farkıyla başlayan iki parçacık, sınırdaki yansımalar nedeniyle kaotik olarak farklılaşan yollar izler. ⓘ

Entropi genel olarak bir sistemin düzensizliğinin ölçüsüdür. İstatistiksel termodinamikte, bazı fiziksel sistemlerin entropisi S şu şekilde tanımlanır

$S=-k\sum _{i}p_{i}\ln(p_{i}).\,$

Toplam, bir kaptaki gaz parçacıklarının konumları gibi söz konusu sistemin tüm olası i durumları üzerinedir. Ayrıca pi, i durumunun elde edilme olasılığı, k ise Boltzmann sabitidir. Benzer şekilde, bilgi teorisindeki entropi de bilgi miktarını ölçer. Bir mesaj alıcısı N olası mesajdan herhangi birini eşit olasılıkla bekleyebilirse, bu tür bir mesaj tarafından iletilen bilgi miktarı log₂ N bit olarak ölçülür. ⓘ

Lyapunov üsleri, dinamik bir sistemin kaotiklik derecesini ölçmek için logaritmaları kullanır. Örneğin, oval bir bilardo masası üzerinde hareket eden bir parçacık için, başlangıç koşullarındaki küçük değişiklikler bile parçacığın çok farklı yollar izlemesine neden olur. Bu tür sistemler deterministik bir şekilde kaotiktir, çünkü başlangıç durumundaki küçük ölçüm hataları tahmin edilebileceği gibi büyük ölçüde farklı nihai durumlara yol açar. Deterministik olarak kaotik bir sistemin en az bir Lyapunov üsteli pozitiftir. ⓘ

Fraktallar

Sierpinski üçgeni (sağda), eşkenar üçgenlerin üç küçük üçgenle tekrar tekrar değiştirilmesiyle oluşturulmuştur. ⓘ

Logaritmalar, fraktalların boyut tanımlarında ortaya çıkar. Fraktallar, küçük parçaların en azından kabaca tüm küresel yapıyı yeniden üretmesi anlamında kendine benzeyen geometrik nesnelerdir. Sierpinski üçgeni (resimde), her biri orijinal uzunluğunun yarısı kadar kenara sahip üç kopyası tarafından kaplanabilir. Bu da bu yapının Hausdorff boyutunu ln(3)/ln(2) ≈ 1.58 yapar. Logaritma tabanlı bir başka boyut kavramı da söz konusu fraktalın kaplanması için gereken kutu sayısının sayılmasıyla elde edilir. ⓘ

Müzik

Doğrusal bir ölçek üzerinde gösterilen dört farklı oktav, daha sonra logaritmik bir ölçek üzerinde gösterilir (kulağın duyduğu gibi). ⓘ

Logaritmalar müzikal tonlar ve aralıklarla ilgilidir. Eşit mizaçta frekans oranı, tek tek tonların spesifik frekansına veya perdesine değil, yalnızca iki ton arasındaki aralığa bağlıdır. Örneğin, A notasının frekansı 440 Hz ve Si bemolün frekansı 466 Hz'dir. A ve Si bemol arasındaki aralık, Si bemol ve B arasındaki aralık gibi bir yarım tondur (frekans 493 Hz). Buna göre, frekans oranları uyuşmaktadır:

${\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.$

Bu nedenle, aralıkları tanımlamak için logaritmalar kullanılabilir: bir aralık, frekans oranının taban-2^1/12 logaritması alınarak yarım ton cinsinden ölçülürken, frekans oranının taban-2^1/1200 logaritması aralığı sent, yani yarım tonun yüzde biri cinsinden ifade eder. İkincisi, eşit olmayan mizaçlar için gerekli olduğundan daha ince kodlama için kullanılır. ⓘ

Aralık (iki ton aynı anda çalınır)	1/12 ton oynat (yardım-bilgi)	Semitone Oyna	Sadece büyük üçüncü Oyna	Büyük üçüncü Oyna	Tritone Oyna	Octave Oyna ⓘ
Frekans oranı r	$2^{\frac {1}{72}}\approx 1.0097$	$2^{\frac {1}{12}}\approx 1.0595$	${\tfrac {5}{4}}=1.25$	${\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}$	${\begin{aligned}2^{\frac {6}{12}}&={\sqrt {2}}\\&\approx 1.4142\end{aligned}}$	$2^{\frac {12}{12}}=2$
Karşılık gelen yarım ton sayısı $\log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)$	${\tfrac {1}{6}}$	$1$	$\approx 3.8631$	$4$	$6$	$12$
Karşılık gelen sent sayısı $\log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)$	$16{\tfrac {2}{3}}$	$100$	$\approx 386.31$	$400$	$600$	$1200$

Sayı teorisi

Doğal logaritma, sayılar teorisinde önemli bir konu olan asal sayıların (2, 3, 5, 7, 11, ...) sayılmasıyla yakından ilişkilidir. Herhangi bir x tamsayısı için, x'ten küçük veya x'e eşit asal sayıların miktarı π(x) olarak gösterilir. Asal sayı teoremi π(x)'in yaklaşık olarak şu şekilde verildiğini ileri sürer

${\frac {x}{\ln(x)}},$

π(x) ile bu kesrin oranının x sonsuza gittiğinde 1'e yaklaşması anlamında. Sonuç olarak, 1 ile x arasında rastgele seçilen bir sayının asal olma olasılığı, x'in ondalık basamak sayısı ile ters orantılıdır. π(x) için çok daha iyi bir tahmin, aşağıdaki şekilde tanımlanan dengelenmiş logaritmik integral fonksiyonu Li(x) tarafından verilir

$\mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln(t)}}\,dt.$

En eski açık matematiksel varsayımlardan biri olan Riemann hipotezi, π(x) ve Li(x)'in karşılaştırılması şeklinde ifade edilebilir. Farklı asal çarpanların sayısını tanımlayan Erdős-Kac teoremi de doğal logaritmayı içerir. ⓘ

n faktöriyelin logaritması, n! = 1 - 2 - ... - n, tarafından verilir

$\ln(n!)=\ln(1)+\ln(2)+\cdots +\ln(n).$

Bu, büyük n için n! 'nin bir yaklaşımı olan Stirling'in formülünü elde etmek için kullanılabilir. ⓘ

Genelleştirmeler

Karmaşık logaritma

z = x + iy'nin kutupsal biçimi. Hem φ hem de φ' z'nin argümanlarıdır. ⓘ

Denklemi çözen tüm a karmaşık sayıları ⓘ

$e^{a}=z$ ⓘ

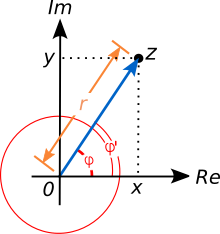
z karmaşık bir sayı olduğunda (olarak kabul edildiğinde), z'nin karmaşık logaritmaları olarak adlandırılır. Karmaşık bir sayı genellikle z = x + iy şeklinde gösterilir; burada x ve y gerçek sayılardır ve i de karesi -1 olan hayali bir birimdir. Böyle bir sayı, sağda gösterildiği gibi karmaşık düzlemde bir nokta ile görselleştirilebilir. Kutupsal form, sıfır olmayan karmaşık bir z sayısını mutlak değeriyle, yani orijine olan (pozitif, reel) r uzaklığıyla ve Re reel (x) ekseni ile hem orijinden hem de z'den geçen doğru arasındaki bir açıyla kodlar. ⓘ

z'nin mutlak değeri r şu şekilde verilir ⓘ

$\textstyle r={\sqrt {x^{2}+y^{2}}}.$ ⓘ

Sinüs ve kosinüsün geometrik yorumunu ve 2π'deki periyodikliklerini kullanarak, herhangi bir karmaşık z sayısı şu şekilde gösterilebilir ⓘ

$z=x+iy=r(\cos \varphi +i\sin \varphi )=r(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )),$ ⓘ

Herhangi bir k tam sayısı için. z argümanının benzersiz bir şekilde belirtilmediği açıktır: hem φ hem de φ = φ + 2kπ tüm k tamsayıları için z'nin geçerli argümanlarıdır, çünkü 2kπ radyan veya φ'ye k⋅360°, orijin etrafında saat yönünün tersine k tur "sarmaya" karşılık gelir. Ortaya çıkan karmaşık sayı, k = 1 için sağda gösterildiği gibi her zaman z'dir. Biri, z'nin olası argümanlarından tam olarak birini, φ'nin uygun bir şekilde seçilmiş bir dönüşe, örneğin -π < φ ≤ π veya 0 ≤ φ < 2π'ye ait olmasını gerektirerek, Arg(z) olarak adlandırılan, büyük A ile gösterilen ana argüman olarak seçebilir. z argümanının tekil olarak belirlendiği bu bölgelere argüman fonksiyonunun dalları denir. ⓘ

Karmaşık logaritmanın ana dalı (-π, π), Log(z). z = 1'deki siyah nokta mutlak değer sıfıra karşılık gelir ve daha parlak renkler daha büyük mutlak değerleri ifade eder. Rengin tonu Log(z) argümanını kodlar. ⓘ

Euler'in formülü trigonometrik fonksiyonlar olan sinüs ve kosinüsü karmaşık üstele bağlar:

$e^{i\varphi }=\cos \varphi +i\sin \varphi .$ ⓘ

Bu formülü ve yine periyodikliği kullanarak, aşağıdaki özdeşlikler geçerlidir:

${\begin{array}{lll}z&=&r\left(\cos \varphi +i\sin \varphi \right)\\&=&r\left(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )\right)\\&=&re^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)}e^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)+i(\varphi +2k\pi )}=e^{a_{k}},\end{array}}$ ⓘ

Burada ln(r) tek reel doğal logaritma, ak z'nin karmaşık logaritmasını gösterir ve k keyfi bir tam sayıdır. Dolayısıyla, e'nin ak'ıncı kuvvetinin z'ye eşit olduğu tüm ak karmaşık değerleri olan z'nin karmaşık logaritmaları sonsuz sayıda değerdir ⓘ

$a_{k}=\ln(r)+i(\varphi +2k\pi ),\quad$ keyfi k tamsayıları için. ⓘ

φ + 2kπ temel argümanlar için tanımlanan aralıkta olacak şekilde k alındığında, ak logaritmanın temel değeri olarak adlandırılır ve yine büyük L ile Log(z) olarak gösterilir. Herhangi bir pozitif reel x sayısının temel argümanı 0'dır; dolayısıyla Log(x) reel bir sayıdır ve reel (doğal) logaritmaya eşittir. Bununla birlikte, çarpımların ve kuvvetlerin logaritmaları için yukarıdaki formüller karmaşık logaritmanın temel değerine genelleştirilmez. ⓘ

Sağdaki çizim Log(z)'yi, z'nin argümanlarını (-π, π] aralığına sınırlayarak göstermektedir. Bu şekilde, karmaşık logaritmanın karşılık gelen dalı, negatif reel x ekseni boyunca süreksizliklere sahiptir, bu da oradaki renk tonundaki sıçramada görülebilir. Bu süreksizlik, bir sınırı geçerken aynı daldaki diğer sınıra atlamaktan, yani sürekli komşu dalın karşılık gelen k değerine geçmemekten kaynaklanır. Böyle bir konuma dal kesimi adı verilir. Argüman üzerindeki aralık kısıtlamalarının kaldırılması, "z argümanı" ve dolayısıyla "z logaritması" ilişkilerini çok değerli fonksiyonlar haline getirir. ⓘ

Diğer üstel fonksiyonların tersleri

Üs alma işlemi matematiğin birçok alanında görülür ve ters fonksiyonu genellikle logaritma olarak adlandırılır. Örneğin, bir matrisin logaritması, matris üstelinin (çok değerli) ters fonksiyonudur. Bir başka örnek de p-adik logaritma, p-adik üstel fonksiyonun ters fonksiyonudur. Her ikisi de reel duruma benzer şekilde Taylor serileri aracılığıyla tanımlanır. Diferansiyel geometri bağlamında, üstel harita bir manifoldun bir noktasındaki teğet uzayı o noktanın bir komşuluğuna eşler. Tersine logaritmik (veya log) harita da denir. ⓘ

Sonlu gruplar bağlamında üstelleştirme, bir b grup elemanının kendisiyle tekrar tekrar çarpılmasıyla verilir. Ayrık logaritma, aşağıdaki denklemi çözen n tamsayısıdır

$b^{n}=x,$

burada x grubun bir elemanıdır. Üs alma işlemi verimli bir şekilde yapılabilir, ancak ayrık logaritmanın bazı gruplarda hesaplanmasının çok zor olduğuna inanılmaktadır. Bu asimetri açık anahtar kriptografisinde önemli uygulamalara sahiptir, örneğin Diffie-Hellman anahtar değişiminde olduğu gibi, kriptografik anahtarların güvenli olmayan bilgi kanalları üzerinden güvenli bir şekilde değiş tokuş edilmesini sağlayan bir rutin. Zech logaritması, sonlu bir alanın sıfır olmayan elemanlarının çarpımsal grubundaki ayrık logaritma ile ilgilidir. ⓘ

Diğer logaritma benzeri ters fonksiyonlar arasında çift logaritma ln(ln(x)), süper veya hiper-4-logaritma (bunun küçük bir varyasyonu bilgisayar biliminde yinelenmiş logaritma olarak adlandırılır), Lambert W fonksiyonu ve logit bulunur. Bunlar sırasıyla çift üstel fonksiyonun, tetrasyonun, f(w) = wew'nin ve lojistik fonksiyonun ters fonksiyonlarıdır. ⓘ

İlgili kavramlar

Grup teorisi açısından bakıldığında, log(cd) = log(c) + log(d) özdeşliği, çarpma altındaki pozitif reeller ile toplama altındaki reeller arasında bir grup izomorfizmini ifade eder. Logaritmik fonksiyonlar bu gruplar arasındaki tek sürekli izomorfizmdir. Bu izomorfizm sayesinde, reeller üzerindeki Haar ölçüsü (Lebesgue ölçüsü) dx, pozitif reeller üzerindeki Haar ölçüsü dx/x'e karşılık gelir. Negatif olmayan reellerin sadece çarpımı değil, aynı zamanda toplamı da vardır ve olasılık semiringi adı verilen bir semiring oluştururlar; bu aslında bir semifield'dir. Logaritma çarpma işlemini toplama işlemine (log çarpma) ve toplama işlemini log toplama işlemine (LogSumExp) dönüştürerek olasılık semirmesi ile log semirmesi arasında bir semirme izomorfizmi oluşturur. ⓘ

Logaritmik tek formlar df/f karmaşık analizde ve cebirsel geometride logaritmik kutupları olan diferansiyel formlar olarak görünür. ⓘ

Polilogaritma şu şekilde tanımlanan fonksiyondur

$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}.$

Doğal logaritma ile Li₁ (z) = -ln(1 - z) ile ilişkilidir. Ayrıca, Lis (1) Riemann zeta fonksiyonu ζ(s)'ye eşittir. ⓘ

Gerekliliği ve tanımı

Logaritma, üstel işlevlerin tersinin hesaplanmasına duyulan ihtiyaç sonucu ortaya çıkmıştır. Örneğin 2'nin küpü 8'dir. Burada 3'ü ifade etmek için logaritmaya ihtiyaç vardır. log₂ 8 = 3. ⓘ

Tarihi

Logaritma, birbirinden habersiz çalışan iki kişi tarafından keşfedilmiştir. Bunlar; 1614’te İskoçyalı John Napier ve 1620’de İsviçreli Joost Bürgi'dir. ⓘ

Logaritma üzerinde önemli çalışmaları olan bir Türk bilgini de Gelenbevi İsmail Efendi'dir. Kendisi büyük bir matematikçi olup, mantıkla da uğraşmıştır. 1730-1790 yıllarında yaşayan bu büyük alimin Logaritma Risalesi isimli çok açık, anlaşılır yazılmış bir eseri mevcuttur. Bu risaledeki metinler, bilim insanlarına hesap yapabilen bir cihaz tasarlama fikrini vermiştir. İsmail Efendi'nin bilim dünyasına bu açıdan bakıldığında büyük katkıları olduğu açıkça fark edilmektedir. Logaritmanın Türkiye'ye gelişine ve uygulanışına dair en detaylı bilgileri veren bilimsel bir makalede bu konu bilim tarihi bakımından ve Salih Murat Üzdilek'in hatıralarıyla beraber açıklanmakta ve Türkiye'de logaritma konusunda ilk çalışmanın Halifezade İsmail Efendi tarafından 1765 yılında yayınlanan Tuhfe-i Behic-i Rasini Tercüme-i Zic-i Kasini adlı yazma tercüme eser olduğu ve logaritmanın Türkiye'ye Batı'dan J. Cassini üzerinden yapılma tercümeyle geldiğini kabul etmek gerektiği gösterilmektedir. ⓘ

Logaritmik özellikler

Logaritma: log₁₀ (sarı),
ln (kırmızı) ve log_½ (mavi) ⓘ

Negatif ve imajiner logaritma

Sonuç

$a^{x}=-b\Rightarrow x=log_{a}b+{\frac {i\pi }{lna}}$ ⓘ

İmajiner logaritma

Sanal logaritma demektir. Sanal sayılar ı içerir. $log_{m}i$ şeklindeki logaritmanın $log_{m}i={\frac {lni}{lnm}}$ şeklinde dönüştürülerek bulunabilir. Negatif logaritmaya benzer bir şekilde Euler özdeşliğinden $i\pi =ln(-1)$ şeklinde bulunmuştu (yukarıda) denklem düzenlenirse $i={\sqrt {-1}}$ den dolayı $i\pi =ln(-1)\Rightarrow i\pi =lni^{2}\Rightarrow {\frac {i\pi }{2}}=lni$ olur. $log_{m}i={\frac {lni}{lnm}}$ denkleminde ln(i) yerine yazılırsa sonuç: $log_{m}i={\frac {i\pi }{2lnm}}$ olur. ⓘ

$log_{i}m$ şeklindeki logaritma ise $log_{i}m={\frac {lnm}{lni}}$ olur. Yani $log_{i}m={\frac {1}{log_{m}i}}$ dir. $log_{m}i={\frac {i\pi }{2lnm}}$ bulunmuştu. Yerine yazılırsa $log_{i}m={\frac {1}{\frac {i\pi }{2lnm}}}$ düzenlenirse $log_{i}m={\frac {2lnm}{i\pi }}$ sonucuna ulaşılır. ⓘ