Altıgen

Düzenli altıgen ⓘ
Düzenli altıgen ⓘ
	Düzgün bir altıgen
Tip	Düzenli çokgen
Kenarlar ve köşeler	6
Schläfli sembolü	{6}, t{3}
Coxeter-Dynkin diyagramları	;
Simetri grubu	Dihedral (D6), sıra 2×6
İç açı (derece)	120°
Özellikler	Dışbükey, döngüsel, eşkenar, izogonal, izotoksal

Altıgen ⓘ

Altıgen çizimi ⓘ

Bir altıgen, altı kenarı ve altı köşesi olan çokgendir. Ayrıca kenarları ve iç açıları eşitse düzgün altıgen olarak adlandırılır. Düzgün altıgenin iç açılarının her biri 120°'dir. Düzgün altıgen altı eşkenar üçgenden oluştuğu için alanı ve çevresi kolayca bulunabilir. Kenarı a uzunlukta olan düzgün bir altıgenin alanı, bir kenarı a olan bir eşkenar üçgenin alanının 6 katına eşittir. İç açıları toplamı 720 derece, bir dış açısının ölçüsü ise 60 derecedir. Dolayısıyla her bir iç açısının ölçüsü 120 derecedir. ⓘ

Düzenli altıgen

Düzgün bir altıgen Schläfli sembolü {6}'ya sahiptir ve aynı zamanda iki tür kenarı değiştiren kesik bir eşkenar üçgen, t{3} olarak da inşa edilebilir. ⓘ

Öklid'in Elementler, Kitap IV, Önerme 15'te verilen pergel ve çizgeç kullanarak düzgün altıgen yapımının adım adım animasyonu: bu, 6

=

2 × 3, iki kuvvet ve farklı Fermat asallarının çarpımı.

AB kenar uzunluğu verildiğinde, A noktasından ve B noktasından dairesel bir yay çizmek M kesişimini, yani çemberin merkezini verir. AB doğru parçasını çember üzerinde dört kez aktarın ve köşe noktalarını birleştirin. ⓘ

Düzgün altıgen, hem eşkenar hem de eşkenar dörtgen olan bir altıgen olarak tanımlanır. İki merkezlidir, yani hem döngüsel (çevrelenmiş bir çembere sahiptir) hem de teğetseldir (yazılı bir çembere sahiptir). ⓘ

Kenarların ortak uzunluğu, çevreleyen dairenin veya çemberin yarıçapına eşittir, bu da ${\tfrac {2}{\sqrt {3}}}$ apotem (yazılı dairenin yarıçapı) ile çarpılır. Tüm iç açılar 120 derecedir. Düzgün bir altıgen, D₆ dihedral grubunu oluşturan altı dönme simetrisine (altı derecelik dönme simetrisi) ve altı yansıma simetrisine (altı simetri çizgisi) sahiptir. Düzgün bir altıgenin, taban tabana zıt köşeleri birleştiren en uzun köşegenleri, bir kenarın iki katı uzunluğundadır. Buradan, bir köşesi düzgün altıgenin merkezinde olan ve altıgenle bir kenarı paylaşan bir üçgenin eşkenar olduğu ve düzgün altıgenin altı eşkenar üçgene bölünebileceği görülebilir. ⓘ

Kareler ve eşkenar üçgenler gibi, düzgün altıgenler de düzlemi döşemek için herhangi bir boşluk olmadan birbirine uyar (her köşede üç altıgen buluşur) ve bu nedenle mozaikler oluşturmak için kullanışlıdır. Bir arı kovanı peteğinin hücreleri bu nedenle ve şeklin alan ve yapı malzemelerini verimli bir şekilde kullanması nedeniyle altıgen şeklindedir. Düzenli bir üçgen kafesin Voronoi diyagramı, altıgenlerin petek mozaiklemesidir. Eşkenar olmasına rağmen genellikle bir triambus olarak kabul edilmez. ⓘ

Parametreler

Maksimum çap (altıgenin uzun köşegenine karşılık gelir), D, kenar uzunluğuna eşit olan maksimum yarıçapın veya çevre yarıçapının (R) iki katıdır, t. Minimum çap veya yazılı dairenin çapı (paralel kenarların ayrılması, düz-düz mesafe, kısa köşegen veya düz bir tabana oturtulduğunda yükseklik), d, minimum yarıçapın veya iç yarıçapın iki katıdır, r. Maksimumlar ve minimumlar aynı faktörle ilişkilidir:

{\frac {1}{2}}d=r=\cos(30^{\circ })R={\frac {\sqrt {3}}{2}}R={\frac {\sqrt {3}}{2}}t

ve benzer şekilde,

d={\frac {\sqrt {3}}{2}}D.

ⓘ

Düzgün bir altıgenin alanı

{\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\[3pt]&={\frac {3{\sqrt {3}}}{8}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {3}}{2}}d^{2}\\[3pt]&\approx 2.598R^{2}\approx 3.464r^{2}\\&\approx 0.6495D^{2}\approx 0.866d^{2}.\end{aligned}}

ⓘ

Herhangi bir düzgün çokgen için alan, a apotemi ve p çevresi cinsinden de ifade edilebilir. Düzgün altıgen için bunlar a = r ve p ${}=6R=4r{\sqrt {3}}$ Yani

{\begin{aligned}A&={\frac {ap}{2}}\\&={\frac {r\cdot 4r{\sqrt {3}}}{2}}=2r^{2}{\sqrt {3}}\\&\approx 3.464r^{2}.\end{aligned}}

ⓘ

Düzenli altıgen kesri doldurur ${\tfrac {3{\sqrt {3}}}{2\pi }}\approx 0.8270$ çevreleyen çemberinin herhangi bir noktasıdır. ⓘ

Eğer düzgün bir altıgenin A, B, C, D, E, F gibi ardışık köşeleri varsa ve P, B ile C arasındaki çember üzerinde herhangi bir nokta ise, PE + PF = PA + PB + PC + PD'dir. ⓘ

Çevre yarıçapının iç yarıçapa oranından, düzgün bir altıgenin yükseklik/genişlik oranının 1:1.1547005 olduğu sonucu çıkar; yani uzun köşegeni 1.0000000 olan bir altıgenin paralel kenarları arasında 0.8660254 mesafe olacaktır. ⓘ

Düzlemdeki nokta

Çevre yarıçaplı düzgün bir altıgenin düzlemindeki rastgele bir nokta için $R$ 'nin düzgün altıgenin merkezine ve altı köşesine olan uzaklıkları $L$ ve $d_{i}$ sırasıyla şunlara sahibiz ⓘ

d_{1}^{2}+d_{4}^{2}=d_{2}^{2}+d_{5}^{2}=d_{3}^{2}+d_{6}^{2}=2\left(R^{2}+L^{2}\right),

d_{1}^{2}+d_{3}^{2}+d_{5}^{2}=d_{2}^{2}+d_{4}^{2}+d_{6}^{2}=3\left(R^{2}+L^{2}\right),

d_{1}^{4}+d_{3}^{4}+d_{5}^{4}=d_{2}^{4}+d_{4}^{4}+d_{6}^{4}=3\left(\left(R^{2}+L^{2}\right)^{2}+2R^{2}L^{2}\right).

ⓘ

Eğer $d_{i}$ düzgün bir altıgenin köşelerinden çevresi üzerindeki herhangi bir noktaya olan uzaklıklar ise ⓘ

\left(\sum _{i=1}^{6}d_{i}^{2}\right)^{2}=4\sum _{i=1}^{6}d_{i}^{4}.

ⓘ

Simetri

Simetriye göre örnek altıgenler ⓘ

d6 izotoksal	g6 yönlendirilmiş	p6 izogonal		d2	g2 genel paralelogon	p2
	r12 düzenli				i4
	g3				a1

Dih₆ veya r12 simetrisine sahip, 12. dereceden düzenli bir altıgenin altı yansıma çizgisi. ⓘ

Dihedral simetriler köşelerden (diyagonal için d) veya kenarlardan (dikler için p) geçip geçmediklerine bağlı olarak bölünmüştür. Orta sütundaki döngüsel simetriler merkezi dönme mertebeleri için g olarak etiketlenmiştir. Düzenli formun tam simetrisi r12'dir ve simetri yok a1 olarak etiketlenmiştir. ⓘ

Düzgün altıgen D₆ simetrisine sahiptir. 16 alt grup vardır. İzomorfizmaya kadar 8 tane vardır: kendisi (D₆), 2 dihedral: (D_3, D₂), 4 döngüsel: (Z₆, Z₃, Z₂, Z₁) ve önemsiz (e) ⓘ

Bu simetriler düzgün bir altıgenin dokuz farklı simetrisini ifade etmektedir. John Conway bunları bir harf ve grup sırasına göre etiketlemiştir. r12 tam simetridir ve a1 simetrisizdir. p6, üç ayna ile inşa edilen izogonal bir altıgen, uzun ve kısa kenarları değiştirebilir ve d6, eşit kenar uzunluklarıyla inşa edilen izotoksal bir altıgendir, ancak köşeler iki farklı iç açıyı değiştirir. Bu iki form birbirinin ikilisidir ve düzgün altıgenin simetri sırasının yarısına sahiptir. i4 formları, bir simetri yönü boyunca düzleştirilmiş veya gerilmiş düzenli altıgenlerdir. Uzatılmış bir eşkenar dörtgen olarak görülebilirken, d2 ve p2 yatay ve dikey olarak uzatılmış uçurtmalar olarak görülebilir. g2 altıgenler, karşılıklı kenarları paralel olan altıgen paralelogonlar olarak da adlandırılır. ⓘ

Her alt grup simetrisi, düzensiz formlar için bir veya daha fazla serbestlik derecesine izin verir. Sadece g6 alt grubunun serbestlik derecesi yoktur ancak yönlendirilmiş kenarlar olarak görülebilir. ⓘ

G2, i4 ve r12 simetrisine sahip altıgenler, paralelogonlar olarak Öklid düzlemini öteleme yoluyla mozaikleyebilir. Diğer altıgen şekilleri düzlemi farklı yönlerde döşeyebilir. ⓘ

p6m (*632)	cmm (2*22)	p2 (2222)	p31m (3*3)	pmg (22*)		pg (××) ⓘ
r12	i4	g2	d2	d2	p2	a1
Dih₆	Dih₂	Z₂	Dih₁			Z₁

A2 ve G2 grupları

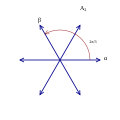A2 grup kökleri	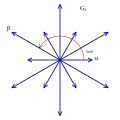G2 grup kökleri

Basit Lie grubu A2'nin 6 kökü, bir Dynkin diyagramı ile temsil edilir düzenli altıgen bir düzen içindedir. İki basit kök arasında 120°'lik bir açı vardır. ⓘ

İstisnai Lie grubu G2'nin 12 kökü, bir Dynkin diyagramı ile temsil edilir aynı zamanda altıgen bir düzen içindedir. İki uzunluktaki iki basit kök arasında 150°'lik bir açı vardır. ⓘ

Diseksiyon

6 küp projeksiyon	12 eşkenar dörtgen diseksiyonu ⓘ

Coxeter, her zonogonun (karşılıklı kenarları paralel ve eşit uzunlukta olan 2m-gon) 1⁄2m(m - 1) paralelkenarlara bölünebileceğini belirtir. Bu durum özellikle eşit sayıda kenarı olan düzgün çokgenler için geçerlidir, bu durumda paralelkenarların hepsi eşkenar dörtgendir. Düzgün bir altıgenin bu ayrışımı, 6 kare yüzden 3'üne sahip bir küpün Petrie çokgen izdüşümüne dayanır. Küpün diğer paralelkenarları ve izdüşümsel yönleri dikdörtgen küboidler içinde parçalara ayrılır. ⓘ

Altıgenlerin üç eşkenar dörtgen ve paralelkenara bölünmesi ⓘ
2D	Rhombs	Paralelkenarlar

	Normal {6}	Altıgen paralelogonlar
3D	Kare yüzler		Dikdörtgen yüzeyler

	Küp		Dikdörtgen küboid

İlgili çokgenler ve eğimler

Düzgün bir altıgenin Schläfli sembolü {6}'dır. Düzgün altıgen, her bir tepe noktası etrafında üç altıgen yüz bulunan {6,3} düzgün altıgen döşemenin bir parçasıdır. ⓘ

Düzgün bir altıgen, Schläfli sembolü t{3} ile kesilmiş bir eşkenar üçgen olarak da oluşturulabilir. İki tip (renk) kenar ile görülen bu form sadece D₃ simetrisine sahiptir. ⓘ

Kesik bir altıgen, t{6}, iki tür (renk) kenarı değişen bir onikigen, {12}'dir. Alternatif bir altıgen, h{6}, bir eşkenar üçgendir, {3}. Düzgün bir altıgen, kenarlarındaki eşkenar üçgenlerle yıldızlandırılarak bir heksagram oluşturulabilir. Bir düzgün altıgen, bir merkez noktası eklenerek altı eşkenar üçgene bölünebilir. Bu desen, düzenli üçgen döşeme içinde tekrar eder. ⓘ

Düzgün bir altıgen, etrafına dönüşümlü kareler ve eşkenar üçgenler eklenerek düzgün bir onikigene genişletilebilir. Bu örüntü eşkenar dörtgen altıgen döşeme içinde tekrar eder. ⓘ

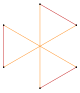
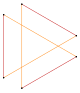
Düzenli {6}	Kesilmiş t{3} = {6}	Hiper kesik üçgenler			Stellated Yıldız figürü 2{3}	Kesilmiş t{6} = {12}	Dönüşümlü h{6} = {3}

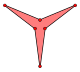
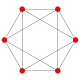
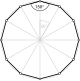
Çapraz altıgen	İçbükey bir altıgen	Kendini kesen bir altıgen (yıldız çokgen)	Genişletilmiş Merkez {6} içinde {12}	Küp içinde bir çarpık altıgen	Disseke {6}	projeksiyon oktahedron	Tam grafik

Kendinden çapraz altıgenler

Düzgün altıgenin köşe düzenine sahip altı adet kendiliğinden kesişen altıgen vardır:

Düzenli köşelere sahip kendiliğinden kesişen altıgenler
Dih₂			Dih₁		Dih_{3 ⓘ}
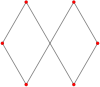Şekil-sekiz	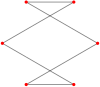Ortadan çevirme	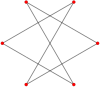Unicursal	Balık kuyruğu	Çift kuyruklu	Üç kuyruklu

Altıgen yapılar

Giant's Causeway yakın çekim ⓘ

Arıların peteklerinden Giant's Causeway'e kadar, altıgen desenler verimlilikleri nedeniyle doğada yaygındır. Altıgen bir ızgarada, geniş bir alan en az altıgenle doldurulacaksa, her çizgi olabildiğince kısadır. Bu da peteklerin yapımı için daha az balmumu gerektirdiği ve sıkıştırma altında daha fazla güç kazandığı anlamına gelir. ⓘ

Karşılıklı kenarları paralel olan düzensiz altıgenlere paralelogon denir ve düzlemi öteleme yoluyla da döşeyebilir. Üç boyutta, paralel karşıt yüzlere sahip altıgen prizmalara paralel yüzlüler denir ve bunlar 3 uzayı öteleme yoluyla mozaikleyebilir. ⓘ

Altıgen prizma mozaikleri
Form	Altıgen döşeme	Altıgen prizmatik bal peteği ⓘ
Düzenli
Paralelogonal

Altıgenlerle mozaiklemeler

Düzlemin benzersiz bir mozaiğini belirleyen düzgün altıgene ek olarak, Conway kriterini karşılayan herhangi bir düzensiz altıgen de düzlemi döşeyecektir. ⓘ

Bir konik kesit içine yerleştirilmiş altıgen

Pascal teoremi ("Hexagrammum Mysticum Teoremi" olarak da bilinir), keyfi bir altıgenin herhangi bir konik kesite yerleştirilmesi ve karşılıklı kenar çiftlerinin birleşene kadar uzatılması durumunda, üç kesişme noktasının düz bir çizgi üzerinde, bu konfigürasyonun "Pascal çizgisi" üzerinde yer alacağını belirtir. ⓘ

Döngüsel altıgen

Lemoine altıgeni, köşeleri bir üçgenin kenarlarının altı kesişimi ve kenarlara paralel olan ve simetri noktasından geçen üç doğru tarafından verilen bir döngüsel altıgendir (bir daire içine yazılmış). ⓘ

Eğer bir döngüsel altıgenin ardışık kenarları a, b, c, d, e, f ise, üç ana köşegen ancak ve ancak ace = bdf ise tek bir noktada kesişir. ⓘ

Bir döngüsel altıgenin her bir kenarı için, bitişik kenarlar kesişme noktalarına kadar uzatılırsa, verilen kenarın dışında bir üçgen oluşturulur, o zaman karşıt üçgenlerin çevrelerini birleştiren segmentler eşzamanlıdır. ⓘ

Eğer bir altıgenin köşeleri bir dar üçgenin çevresi üzerinde, üçgenin genişletilmiş yüksekliklerinin çevresi ile birleştiği altı noktada (üç üçgen köşesi dahil) bulunuyorsa, o zaman altıgenin alanı üçgenin alanının iki katıdır. ⓘ

Konik bir kesite teğet altıgen

ABCDEF bir konik kesitin altı teğet doğrusundan oluşan bir altıgen olsun. O zaman Brianchon teoremi üç ana köşegen AD, BE ve CF'nin tek bir noktada kesiştiğini belirtir. ⓘ

Bir çembere teğet olan ve a, b, c, d, e ve f ardışık kenarlarına sahip bir altıgende, ⓘ

a+c+e=b+d+f.

ⓘ

Rastgele bir altıgenin kenarlarındaki eşkenar üçgenler

Rastgele bir altıgenin kenarlarındaki eşkenar üçgenler ⓘ

Herhangi bir altıgenin her bir kenarına dışarıdan bir eşkenar üçgen inşa edilirse, karşıt üçgenlerin merkezlerini birleştiren segmentlerin orta noktaları başka bir eşkenar üçgen oluşturur. ⓘ

Eğri altıgen

Üçgen antiprizmanın kenarları (siyah) olarak görülen düzenli bir çarpık altıgen, simetri D_3d, [2⁺,6], (2*3), sıra 12. ⓘ

Çarpık altıgen, altı köşesi ve kenarı olan ancak aynı düzlemde bulunmayan bir çarpık çokgendir. Böyle bir altıgenin içi genellikle tanımlı değildir. Çarpık zig-zag altıgenin köşeleri iki paralel düzlem arasında değişir. ⓘ

Düzenli bir çarpık altıgen, eşit kenar uzunlukları ile köşe geçişlidir. Üç boyutta bu bir zig-zag çarpık altıgen olacaktır ve aynı D_3d, [2⁺,6] simetri, sıra 12 ile üçgen bir antiprizmanın köşelerinde ve yan kenarlarında görülebilir. ⓘ

Küp ve oktahedron (üçgen antiprizma ile aynı) petrie çokgenleri olarak düzenli çarpık altıgenlere sahiptir. ⓘ

3 katlı eksenlerde eğri altıgenler ⓘ
Küp	Oktahedron

Petrie çokgenleri

Düzenli çarpık altıgen, bu çarpık ortogonal izdüşümlerde gösterilen bu yüksek boyutlu düzenli, düzgün ve çift çokyüzlüler ve politoplar için Petrie çokgenidir:

4D		5D ⓘ
3-3 duoprizm	3-3 duopyramid	5-simpleks

Dışbükey eşkenar altıgen

Bir altıgenin ana köşegeni, altıgeni dörtgenlere bölen bir köşegendir. Ortak kenarı a olan herhangi bir dışbükey eşkenar altıgende (tüm kenarları eşit olan), öyle bir d₁ asal köşegeni vardır ki ⓘ

{\frac {d_{1}}{a}}\leq 2

ⓘ

ve bir ana köşegen d₂ öyle ki ⓘ

{\frac {d_{2}}{a}}>{\sqrt {3}}.

ⓘ

Altıgenler ile çokyüzlüler

Sadece düzgün altıgenlerden oluşan Platonik bir katı yoktur, çünkü altıgenler mozaiklenir ve sonucun "katlanmasına" izin vermez. Bazı altıgen yüzlere sahip Arşimet katıları kesik dörtyüzlü, kesik oktahedron, kesik ikosahedron (futbol topu ve fulleren şöhreti), kesik küboktahedron ve kesik ikosidodekahedrondur. Bu altıgenler, Coxeter diyagramları şu şekilde olan kesik üçgenler olarak düşünülebilir ve . ⓘ

Arşimet katılarında altıgenler ⓘ
Tetrahedral	Oktahedral		İkozahedral

kesilmiş tetrahedron	kesik oktahedron	kesilmiş küboktahedron	kesik ikosahedron	kesilmiş ikosidodekahedron

Bu Goldberg çokyüzlüsü G(2,0) gibi gerilmiş veya düzleştirilmiş altıgenlere sahip başka simetri çokyüzlüleri de vardır:

Goldberg çokyüzlülerinde altıgenler ⓘ
Tetrahedral	Oktahedral	İkozahedral
Pahlı tetrahedron	Pahlı küp	Pahlı dodekahedron

Ayrıca düzenli altıgenlere sahip 9 Johnson katı vardır:

Altıgenli Johnson katıları ⓘ
üçgen kubbe	uzatılmış üçgen kubbe	cayro uzatmali üçgen kubbe
büyütülmüş altıgen prizma	parabiaugmente altıgen prizma	metabiyolojik olarak büyütülmüş altıgen prizma	üç katlı altıgen prizma
artırılmış kesilmiş tetrahedron	üçgen hebesphenorotunda	Kesilmiş triakis tetrahedron

Altıgenler ile Prizmoidler ⓘ
Altıgen prizma	Altıgen antiprizma	Altıgen piramit

Düzenli altıgenlerle kaplamalar ⓘ
Düzenli	1- tekdüze
{6,3}	r{6,3}	rr{6,3}	tr{6,3}

2- tekdüze eğimler

Doğal ve yapay altıgenler galerisi

Grafenin ideal kristal yapısı altıgen bir ızgaradır.
Birleştirilmiş E-ELT ayna segmentleri
Bir arı kovanı peteği
Bir kaplumbağanın kabuğunun kabukları
Satürn'ün altıgeni, gezegenin kuzey kutbu etrafında altıgen bir bulut deseni
Bir kar tanesinin mikrografı
Benzen, altıgen şekle sahip en basit aromatik bileşik.
Bir köpükteki kabarcıkların altıgen düzeni.
Altıgen aromatik halkalardan oluşan bir moleküler altıgenin kristal yapısı.
Kuzey İrlanda'daki Giant's Causeway'den doğal olarak oluşmuş bazalt sütunlar; büyük kütlelerin çokgen bir kırılma deseni oluşturması için yavaş soğuması gerekir
Dry Tortugas Ulusal Parkı'ndaki Jefferson Kalesi'nin havadan görünümü
James Webb Uzay Teleskobu aynası 18 altıgen parçadan oluşmaktadır.
Metropolitan Fransa belli belirsiz altıgen bir şekle sahiptir. Fransızca'da l'Hexagone, Fransa'nın Avrupa anakarasını ifade eder.
Altıgen Hanksit kristali, birçok altıgen kristal sistemi mineralinden biri
Altıgen ahır
The Hexagon, Reading, Berkshire'da altıgen bir tiyatro
Władysław Gliński'nin altıgen satrancı
Tayvan Botanik Bahçelerindeki Pavyon
Altıgen pencere ⓘ