Beşgen

Düz/>Düzgün bir beşgen
Kenarları ve köşeleri	5
Boyutları	(D5)
Alanı	${\frac {t^{2}{\sqrt {25+10{\sqrt {5}}}}}{4}}$
İç açıları toplamı	540°

Bir beşgen, beş kenarı olan çokgendir. İç açıları toplamı 540°, dış açıların toplamı ise 360°'dir. ⓘ

Pentagon ⓘ
Döngüsel bir beşgen
Kenarlar ve köşeler	5

Bir beşgen basit veya kendisiyle kesişen olabilir. Kendini kesen düzgün beşgene (veya yıldız beşgene) pentagram denir. ⓘ

Düzenli beşgenler

Normal beşgen ⓘ
Düzgün bir beşgen
Tip	Düzenli çokgen
Kenarlar ve köşeler	5
Schläfli sembolü	{5}
Coxeter-Dynkin diyagramları
Simetri grubu	Dihedral (D5), sıra 2×5
İç açı (derece)	108°
Özellikler	Dışbükey, döngüsel, eşkenar, izogonal, izotoksal

Yan ($t$), circumradius ($R$), yazılı daire yarıçapı ($r$), yükseklik ($R+r$), genişlik / diyagonal ($\varphi t$) ⓘ

Düzgün bir beşgenin Schläfli sembolü {5} ve iç açıları 108°'dir. ⓘ

Düzgün bir beşgenin beş yansıma simetrisi çizgisi ve 5. dereceden dönme simetrisi vardır (72°, 144°, 216° ve 288° boyunca). Dışbükey düzgün beşgenin köşegenleri kenarlarına altın orandadır. Kenar uzunluğu göz önüne alındığında $t,$ yüksekliği $H$ (bir kenardan karşı tepe noktasına olan mesafe), genişlik $W$ (en uzak iki nokta arasındaki mesafe, köşegen uzunluğuna eşittir $D$) ve circumradius $R$ tarafından verilir:

${\begin{aligned}H&={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}~t\approx 1.539~t,\\W=D&={\frac {1+{\sqrt {5}}}{2}}~t\approx 1.618~t,\\W&={\sqrt {2-{\frac {2}{\sqrt {5}}}}}\cdot H\approx 1.051~H,\\R&={\sqrt {\frac {5+{\sqrt {5}}}{10}}}t\approx 0.8507~t,\\D&=R\ {\sqrt {\frac {5+{\sqrt {5}}}{2}}}=2R\cos 18^{\circ }=2R\cos {\frac {\pi }{10}}\approx 1.902~R.\end{aligned}}$ ⓘ

Kenar uzunluğuna sahip dışbükey düzgün beşgenin alanı $t$ tarafından verilir

${\begin{aligned}A&={\frac {t^{2}{\sqrt {25+10{\sqrt {5}}}}}{4}}={\frac {5t^{2}\tan 54^{\circ }}{4}}\\&={\frac {{\sqrt {5(5+2{\sqrt {5}})}}\;t^{2}}{4}}\approx 1.720~t^{2}.\end{aligned}}$ ⓘ

Eğer circumradius $R$ düzgün bir beşgen verildiğinde, kenar uzunluğu $t$ ifadesi ile bulunur

$t=R\ {\sqrt {\frac {5-{\sqrt {5}}}{2}}}=2R\sin 36^{\circ }=2R\sin {\frac {\pi }{5}}\approx 1.176~R,$ ⓘ

ve alanı ⓘ

$A={\frac {5R^{2}}{4}}{\sqrt {\frac {5+{\sqrt {5}}}{2}}};$ ⓘ

çünkü çevreleyen dairenin alanı $\pi R^{2},$ düzgün beşgen, çevrelediği dairenin yaklaşık 0,7568'ini doldurur. ⓘ

Alan formülünün türetilmesi

Herhangi bir düzgün çokgenin alanı şöyledir:

$A={\frac {1}{2}}Pr$ ⓘ

Burada P çokgenin çevresi, r ise iç yarıçapıdır (eşdeğer olarak apotem). Düzgün beşgenin P ve r değerlerini yerine koyduğumuzda aşağıdaki formül elde edilir

$A={\frac {1}{2}}\cdot 5t\cdot {\frac {t\tan {\mathord {\left({\frac {3\pi }{10}}\right)}}}{2}}={\frac {5t^{2}\tan {\mathord {\left({\frac {3\pi }{10}}\right)}}}{4}}$

kenar uzunluğu t olan. ⓘ

Inradius

Her düzgün dışbükey çokgende olduğu gibi, düzgün dışbükey beşgenin de yazılı bir dairesi vardır. Düzgün bir beşgenin apotemi, yani yazılı dairenin yarıçapı r, kenar uzunluğu t ile şu şekilde ilişkilidir ⓘ

$r={\frac {t}{2\tan {\mathord {\left({\frac {\pi }{5}}\right)}}}}={\frac {t}{2{\sqrt {5-{\sqrt {20}}}}}}\approx 0.6882\cdot t.$ ⓘ

Dairesel çemberden köşelere giden akorlar

Her düzgün dışbükey çokgen gibi düzgün dışbükey beşgenin de bir çevre dairesi vardır. Ardışık köşeleri A, B, C, D, E olan bir düzgün beşgen için P, B ve C noktaları arasındaki çember üzerinde herhangi bir nokta ise, PA + PD = PB + PC + PE. ⓘ

Düzlemdeki nokta

Çevre yarıçaplı düzgün bir beşgenin düzlemindeki rastgele bir nokta için $R$'nin düzgün beşgenin merkezine ve beş köşesine olan uzaklıkları $L$ ve $d_{i}$ sırasıyla şunlara sahibiz ⓘ

${\begin{aligned}\textstyle \sum _{i=1}^{5}d_{i}^{2}&=5\left(R^{2}+L^{2}\right),\\\textstyle \sum _{i=1}^{5}d_{i}^{4}&=5\left(\left(R^{2}+L^{2}\right)^{2}+2R^{2}L^{2}\right),\\\textstyle \sum _{i=1}^{5}d_{i}^{6}&=5\left(\left(R^{2}+L^{2}\right)^{3}+6R^{2}L^{2}\left(R^{2}+L^{2}\right)\right),\\\textstyle \sum _{i=1}^{5}d_{i}^{8}&=5\left(\left(R^{2}+L^{2}\right)^{4}+12R^{2}L^{2}\left(R^{2}+L^{2}\right)^{2}+6R^{4}L^{4}\right).\end{aligned}}$ ⓘ

Eğer $d_{i}$ düzgün bir beşgenin köşelerinden çevresi üzerindeki herhangi bir noktaya olan uzaklıklar ise ⓘ

$3\left(\textstyle \sum _{i=1}^{5}d_{i}^{2}\right)^{2}=10\textstyle \sum _{i=1}^{5}d_{i}^{4}.$ ⓘ

Geometrik yapılar

Düzgün beşgen, 5 bir Fermat asalı olduğu için pergel ve çizgeç ile inşa edilebilir. Düzgün beşgen oluşturmak için çeşitli yöntemler bilinmektedir. Bazıları aşağıda tartışılmıştır. ⓘ

Richmond'un yöntemi

Belirli bir daire içinde düzgün bir beşgen oluşturmanın bir yöntemi Richmond tarafından tanımlanmış ve Cromwell's Polyhedra'da daha ayrıntılı olarak tartışılmıştır. ⓘ

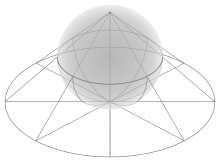
Üst panel, Richmond'un yönteminde yazılı beşgenin kenarını oluşturmak için kullanılan yapıyı göstermektedir. Beşgeni tanımlayan çember birim yarıçapa sahiptir. Merkezi C noktasında bulunur ve yarıçapının yarısında bir orta nokta M işaretlenmiştir. Bu nokta, D noktasında merkezin üzerinde dikey olarak çevreyle birleştirilir. CMD açısı ikiye bölünür ve açıortay dikey ekseni Q noktasında keser. Q'dan geçen yatay bir çizgi çemberi P noktasında keser ve PD kirişi yazılı beşgenin gerekli kenarıdır. ⓘ

Bu kenarın uzunluğunu belirlemek için DCM ve QCM dik üçgenleri dairenin altında gösterilir. Pisagor teoremi ve iki kenar kullanılarak, büyük üçgenin hipotenüsü şu şekilde bulunur $\scriptstyle {\sqrt {5}}/2$. Daha sonra küçük üçgenin h kenarı yarım açı formülü kullanılarak bulunur:

$\tan(\phi /2)={\frac {1-\cos(\phi )}{\sin(\phi )}}\ ,$ ⓘ

Burada ϕ'nin kosinüs ve sinüsü büyük üçgenden bilinmektedir. Sonuç şudur:

$h={\frac {{\sqrt {5}}-1}{4}}\ .$ ⓘ

Eğer DP gerçekten düzgün bir beşgenin kenarı ise, $m\angle \mathrm {CDP} =54^{\circ }$Böylece DP = 2 cos(54°), QD = DP cos(54°) = 2cos²(54°) ve CQ = 1 - 2cos²(54°), kosinüs çift açı formülüne göre -cos(108°)'ye eşittir. Bu, 72°'nin kosinüsüdür, yani $\left({\sqrt {5}}-1\right)/4$ istenildiği gibi. ⓘ

Carlyle çemberleri

Carlyle dairelerini kullanan yöntem ⓘ

Carlyle dairesi, ikinci dereceden bir denklemin köklerini bulmak için geometrik bir yöntem olarak icat edilmiştir. Bu metodoloji, düzenli bir beşgen oluşturmak için bir prosedüre yol açar. Adımlar aşağıdaki gibidir:

1. Beşgenin içine yerleştirileceği bir daire çizin ve O merkez noktasını işaretleyin.
2. Dairenin merkezinden geçen yatay bir çizgi çizin. Daire ile sol kesişme noktasını B noktası olarak işaretleyin.
3. Merkezden geçen dikey bir çizgi oluşturun. Daire ile bir kesişme noktasını A noktası olarak işaretleyin.
4. O ve B'nin orta noktası olarak M noktasını oluşturun.
5. A noktasından geçen M merkezli bir çember çizin. Çemberin yatay çizgi ile kesişimini (orijinal çemberin içinde) W noktası olarak ve çemberin dışındaki kesişimini V noktası olarak işaretleyin.
6. Yarıçapı OA ve merkezi W olan bir daire çizin. Bu daire orijinal daireyi beşgenin iki köşesinde keser.
7. Yarıçapı OA ve merkezi V olan bir çember çizin. Bu çember orijinal çemberi beşgenin iki köşesinde keser.
8. Beşinci köşe, yatay çizginin orijinal çemberle en sağdaki kesişme noktasıdır.

Adım 6-8, animasyonda gösterilen aşağıdaki versiyona eşdeğerdir:

6a. F noktasını O ve W'nin orta noktası olarak oluşturun. ⓘ

7a. F'den geçen dikey bir çizgi oluşturun. Bu çizgi orijinal daireyi beşgenin iki köşesinde keser. Üçüncü köşe, yatay çizginin orijinal daire ile en sağdaki kesişme noktasıdır. ⓘ

8a. Pergeli ve adım 7a'da bulunan köşe uzunluğunu kullanarak diğer iki köşeyi oluşturun. ⓘ

Öklid'in yöntemi

Öklid'in altın üçgeni kullanarak belirli bir çemberde beşgen için yöntemi, animasyon 1 dakika 39 saniye ⓘ

Düzgün bir beşgen, pergel ve çizgeç kullanılarak ya belirli bir dairenin içine yazılarak ya da belirli bir kenar üzerine inşa edilerek oluşturulabilir. Bu süreç Öklid tarafından MÖ 300 civarında Elementler adlı eserinde tanımlanmıştır. ⓘ

Fiziksel yapım yöntemleri

Kağıt şeridin üstten düğümü ⓘ

• Sadece bir kağıt şeridinden, şeride üstten bir düğüm atarak ve kağıt şeridin uçlarını çekerek düğümü dikkatlice düzleştirerek düzenli bir beşgen oluşturulabilir. Uçlardan biri beşgenin üzerine geri katlandığında arkadan aydınlatıldığında bir pentagram ortaya çıkacaktır.
• Sert kağıt veya kart üzerine düzgün bir altıgen oluşturun. Karşılıklı köşeler arasındaki üç çap boyunca kırışın. Eşkenar üçgen bir kanat yapmak için bir köşeden merkeze doğru kesin. Beşgen bir piramit yapmak için bu kanadı komşusunun altına sabitleyin. Piramidin tabanı düzgün bir beşgendir. ⓘ

Simetri

Düzenli bir beşgenin simetrileri. Köşeler simetri konumlarına göre renklendirilmiştir. Köşeler ve kenarlar boyunca mavi ayna çizgileri çizilmiştir. Dönme sıraları merkezde verilmiştir. ⓘ

Düzgün beşgen 10. dereceden Dih₅ simetrisine sahiptir. 5 asal sayı olduğu için dihedral simetriye sahip bir alt grup vardır: Dih₁ ve 2 döngüsel grup simetrisi: Z₅ ve Z₁. ⓘ

Bu 4 simetri beşgen üzerinde 4 farklı simetride görülebilir. John Conway bunları bir harf ve grup sırasına göre etiketlemiştir. Düzenli formun tam simetrisi r10'dur ve simetri yok a1 olarak etiketlenmiştir. Dihedral simetriler köşelerden (diyagonal için d) veya kenarlardan (dikler için p) geçip geçmediklerine ve yansıma çizgileri hem kenarlardan hem de köşelerden geçtiğinde i'ye bağlı olarak bölünür. Orta sütundaki döngüsel simetriler merkezi dönme mertebeleri için g olarak etiketlenmiştir. ⓘ

Her bir alt grup simetrisi düzensiz formlar için bir veya daha fazla serbestlik derecesine izin verir. Sadece g5 alt grubunun serbestlik derecesi yoktur ancak yönlendirilmiş kenarlar olarak görülebilir. ⓘ

Düzenli pentagram

Bir pentagram veya beşgen, düzenli bir yıldız beşgendir. Schläfli sembolü {5/2}'dir. Kenarları düzenli bir dışbükey beşgenin köşegenlerini oluşturur - bu düzenlemede iki beşgenin kenarları altın orandadır. ⓘ

Eşkenar beşgenler

Zincir şeklinde yerleştirilmiş dört eşit daireden oluşan eşkenar beşgen. ⓘ

Eşkenar beşgen, beş kenarı eşit uzunlukta olan bir çokgendir. Bununla birlikte, beş iç açısı bir dizi değer kümesi alabilir, böylece bir beşgen ailesi oluşturmasına izin verir. Buna karşılık, düzgün beşgen benzerliğe kadar benzersizdir, çünkü eşkenar ve eşkenar dörtgendir (beş açısı eşittir). ⓘ

Döngüsel beşgenler

Döngüsel beşgen, çevre çemberi adı verilen bir çemberin beş köşenin tamamından geçtiği beşgendir. Düzgün beşgen, döngüsel beşgene bir örnektir. Düzgün olsun ya da olmasın, döngüsel bir beşgenin alanı, katsayıları beşgenin kenarlarının fonksiyonları olan septik bir denklemin köklerinden birinin karekökünün dörtte biri olarak ifade edilebilir. ⓘ

Rasyonel kenarlara ve rasyonel alana sahip döngüsel beşgenler vardır; bunlara Robbins beşgenleri denir. Bir Robbins beşgeninin köşegenlerinin ya tümünün rasyonel ya da tümünün irrasyonel olması gerektiği kanıtlanmıştır ve tüm köşegenlerin rasyonel olması gerektiği varsayılmaktadır. ⓘ

Genel dışbükey beşgenler

Tüm dışbükey beşgenler için, köşegenlerin karelerinin toplamı, kenarların karelerinin toplamının 3 katından daha azdır. ⓘ

Döşemede beşgenler

Bir düzlem üzerinde eşit boyutlu düzgün beşgenlerin en iyi bilinen paketlenmesi, düzlemin %92,131'ini kaplayan çift kafesli bir yapıdır. ⓘ

Düzgün bir beşgen, düzgün çokgenlerden oluşan herhangi bir döşemede yer alamaz. İlk olarak, bir beşgenin düzgün bir döşeme (tüm yüzlerin eş olduğu, dolayısıyla tüm çokgenlerin beşgen olmasını gerektiren bir döşeme) oluşturamayacağını kanıtlamak için, 360° / 108° = 31⁄3 (burada 108° iç açıdır) olduğunu gözlemleyin, ki bu tam sayı değildir; dolayısıyla tek bir köşeyi paylaşan ve aralarında boşluk bırakmayan tam sayıda beşgen yoktur. Daha da zor olanı, bir beşgenin düzgün çokgenler tarafından yapılan herhangi bir kenardan kenara döşemede yer alamayacağını kanıtlamaktır: Düzgün bir beşgenin bilinen maksimum paketleme yoğunluğu yaklaşık 0,921'dir ve gösterilen çift kafes paketleme ile elde edilir. Thomas Hales ve Wöden Kusner, 2016 yılında yayınladıkları bir ön baskıda, düzgün beşgenin çift kafesli paketlemesinin ("beşgen buz ışını" paketlemesi olarak adlandırdıkları ve 1900'de Çinli zanaatkârların çalışmalarına dayandırdıkları) düzlemdeki tüm düzgün beşgen paketlemeleri arasında en uygun yoğunluğa sahip olduğuna dair bir kanıt açıkladılar. 2020 itibariyle, kanıtları henüz hakemlikten geçmemiş ve yayınlanmamıştır. ⓘ

Beşgen içeren bir tepe noktasında 4 veya daha fazla buluşan düzgün çokgen kombinasyonu yoktur. 3'lü kombinasyonlar için, 3 çokgen bir tepe noktasında buluşuyorsa ve birinin tek sayıda kenarı varsa, diğer 2'si uyumlu olmalıdır. Bunun nedeni, beşgenin kenarlarına değen çokgenlerin beşgenin etrafında sıralanması gerektiğidir ki bu da beşgenin tek kenar sayısı nedeniyle imkansızdır. Beşgen için bu, tüm açıları (360 - 108) / 2 = 126° olan bir çokgenle sonuçlanır. Bu çokgenin sahip olduğu kenar sayısını bulmak için sonuç 360 / (180 - 126) = 62⁄3 olur ki bu da tam sayı değildir. Bu nedenle beşgen, düzgün çokgenlerden oluşan hiçbir döşemede yer alamaz. ⓘ

Düzlemi tek yüzlü olarak döşeyebilen 15 sınıf beşgen vardır. Beşgenlerin hiçbiri genel olarak herhangi bir simetriye sahip değildir, ancak bazılarının ayna simetrisine sahip özel durumları vardır. ⓘ

15 tek yüzlü beşgen karo

1	2	3	4	5 ⓘ
6	7	8	9	10
11	12	13	14	15

Çokyüzlülerde beşgenler

Ih	Th	Td	O	I	D5d ⓘ
Dodecahedron	Pyritohedron	Tetartoid	Beşgen ikositetrahedron	Beşgen altı yüzlü	Kesik trapez yüzlü

Doğadaki beşgenler

Bitkiler

• 

  Bamyanın beşgen kesiti.

• 

  Sabah sefaları, diğer birçok çiçek gibi, beşgen bir şekle sahiptir.

• 

  Bir elmanın gynoecium'u beş köşeli bir yıldız şeklinde düzenlenmiş beş karpel içerir

• 

  Yıldız meyvesi de beş katlı simetriye sahip bir başka meyvedir. ⓘ

• 

  Bamya

• 

  Bamya çiçeği

• 

  Elmanın ortadan bölünce görülen çekirdek kısmı ⓘ

Hayvanlar

• 

  Bir deniz yıldızı. Birçok ekinoderm beş katlı radyal simetriye sahiptir.

• 

  Başka bir ekinoderm örneği, bir deniz kestanesi iç iskeleti.

• 

  Yine beşgen şekilli ekinodermler olan kırılgan yıldızların bir örneği. ⓘ

Mineraller

• 

  Beşgen dodekahedron olarak oluşturulmuş bir Ho-Mg-Zn ikozahedral kuasikristal. Yüzler gerçek düzenli beşgenlerdir.

• 

  Piritin piritohedral bir kristali. Bir piritohedron, düzenli olmak için kısıtlanmamış 12 özdeş pentagonal yüze sahiptir. ⓘ

Diğer örnekler

• 

  Pentagon, Amerika Birleşik Devletleri Savunma Bakanlığı'nın merkezi.

• 

  Bir beyzbol sahasının ana kalesi ⓘ